4.3: Área de un Sector
- Page ID
- 113499
En geometría aprendiste que el área de un círculo de radio\(r \) es\(\pi r^2 \). Ahora aprenderemos a encontrar el área de un sector de un círculo. Un sector es la región delimitada por un ángulo central y su arco interceptado, como la región sombreada en la Figura 4.3.1.
Dejar\(\theta \) ser un ángulo central en un círculo de radio\(r \) y dejar\(A \) ser el área de su sector. Similar a la longitud del arco, la relación de\(A \) al área de todo el círculo es la misma que la relación de\(\theta \) a una revolución. En otras palabras, utilizando de nuevo la medida de radianes,
\ [\ frac {\ text {área del sector}} {\ text {área de círculo entero}} ~=~
\ frac {\ text {ángulo del sector}} {\ text {una revolución}}\ quad\ Rightarrow\ quad
\ frac {A} {\ pi\, r^2} ~=~\ frac {\ theta} {2\ pi} ~.
\ nonumber\]
Resolviendo para\(A \) en la ecuación anterior, obtenemos la siguiente fórmula:
En un círculo de radio\(r \), el área\(A \) del sector dentro de un ángulo central\(\theta \) es
\[ A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~,\label{eqn:sectorarea} \]
donde\(\theta \) se mide en radianes.
Encuentra el área de un sector cuyo ángulo es\(\frac{\pi}{5} \) rad en un círculo de radio\(4\) cm.
Solución
Usando\(\theta=\frac{\pi}{5} \) y\(r=4 \) en la Ecuación\ ref {eqn:sectorarea}, el área\(A \) del sector es
\ [A ~=~\ tfrac {1} {2}\, r^2\;\ theta ~=\ tfrac {1} {2}\, (4) ^2\;\ cdot\;\ tfrac {\ pi} {5}
~=~\ en caja {\ tfrac {8\ pi} {5} ~\ texto {cm} ^2} ~.
\ nonumber\]
Encuentra el área de un sector cuyo ángulo está\(117^\circ \) en un círculo de radio\(3.5 \) m.
Solución:
Al igual que con la longitud del arco, tenemos que asegurarnos de que el ángulo se mida en radianes o de lo contrario la respuesta estará muy alejada. Entonces convirtiendo\(\theta=117^\circ \) a radianes y usando\(r=3.5 \) en la Ecuación\ ref {eqn:sectorarea} para el área\(A \) del sector, obtenemos
\ [\ theta ~=~ 117^\ circ ~=~\ frac {\ pi} {180}\;\ cdot\; 117 ~=~ 2.042~\ text {rad}
\ quad\ Rightarrow\ quad
A ~=~\ tfrac {1} {2}\, r^2\;\ theta ~=\ tfrac {1} {2}\, (3.5) ^2\ ;( 2.042)
~=~\ en caja {12.51~\ texto {m} ^2} ~.
\ nonumber\]
Para un sector cuyo ángulo está\(\theta \) en un círculo de radio\(r \), la longitud del arco cortado por ese ángulo es\(s=r\,\theta \). Así, por Ecuación\ ref {eqn:sectorarea} el área\(A \) del sector puede escribirse como:
\ [
\ en caja {A ~=~\ tfrac {1} {2}\, rs}\ etiqueta {eqn:sectorarc}
\ nonumber\]
Nota: El ángulo central\(\theta \) que intercepta un arco a veces se llama el ángulo subtendido por el arco.
Encuentra el área de un sector cuyo arco es\(6 \) cm en un círculo de radio\(9 \) cm.
Solución
Usando\(s=6 \) y\(r=9 \) en la Ecuación\ ref {eqn:sectorarc} para el área\(A \), obtenemos
\ [A ~=~\ tfrac {1} {2}\, rs ~=~ ~=~\ tfrac {1} {2}\, (9)\, (6) ~=~\ en caja {27~\ texto {cm} ^2} ~.
\ nonumber\]
Tenga en cuenta que el ángulo subtendido por el arco es\(\theta = \frac{s}{r} = \frac{2}{3} \) rad.
Encuentre el área\(K \) dentro del sistema de poleas de correa del Ejemplo 4.7 en la Sección 4.2.
Solución:
Recordemos que las poleas de correa tienen radios de\(5 \) cm y\(8 \) cm, y sus centros están separados por\(15 \) cm. Mostramos en el Ejemplo 4.7 eso\(EF=AC=6\,\sqrt{6} \),\(\angle\,DAE=1.37 \) rad, y\(\angle\,GBF=1.77 \) rad. Vemos de la Figura 4.3.2 que, por simetría, el área total\(K \) encerrada por el cinturón es el doble del área por encima de la línea\(\overline{DG} \), es decir,
\ [\ nonumber\ begin {align*}
K ~=~ 2\, ((&\ text {Área del sector\(DAE\)}) ~+~ (\ text {Área del rectángulo\(AEFC\)})\\ nonumber
&+~ (\ text {Área del triángulo\(\triangle\,ABC\)}) ~+~ (\ text {Área del sector\(GBF\)})) ~.
\ end {align*}\ nonumber\]
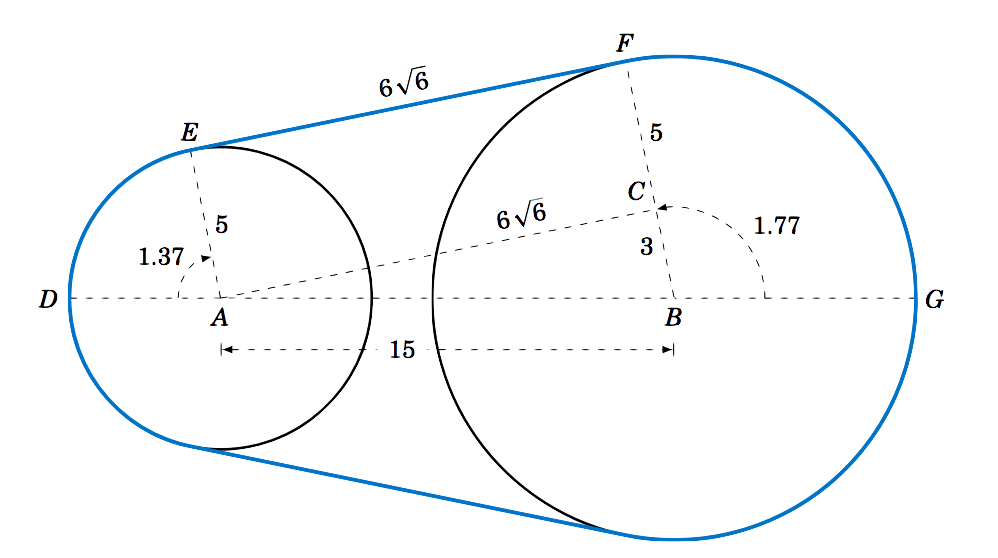
Ya que\(AEFC \) es un rectángulo con lados\(5 \) y\(6\,\sqrt{6} \), su área es\(30\,\sqrt{6} \). Y ya que\(\triangle\,ABC \) es un triángulo rectángulo cuyas patas tienen longitudes\(3 \) y\(6\,\sqrt{6} \), su área es\(\frac{1}{2}\,(3)\,(6\,\sqrt{6}) = 9\,\sqrt{6} \). Así, usando la ecuación\ ref {eqn:sectorarea} para las áreas de sectores\(DAE \) y\(GBF \), tenemos
\ [\ nonumber\ begin {align*}
K ~&=~ 2\,\ left ((\ text {Área del sector\(DAE\)})\; +\; 30\,\ sqrt {6}\; +\; +\; 9\,\ sqrt {6}\; +\;
(\ text {Área del sector\(GBF\)})\ derecha)\\ nonumber
&=~ 2\,\ izquierda (\ tfrac {1} {2}\, (5) ^2\, (1.37) ~+~ 30\,\ sqrt {6} ~+~ 9\,\ sqrt {6} ~+~
\ tfrac {1} {2}\, (8) ^2\, (1.77)\ derecha)\\ nonumber
&=~\ en caja {338.59~\ texto {cm} ^2} ~.
\ end {align*}
\ nonumber\]
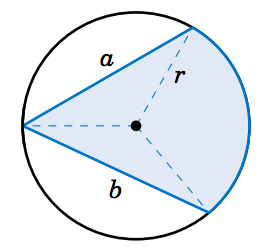
Hasta el momento hemos tratado con el área cortada por un ángulo central. ¿Cómo encontraría el área de una región cortada por un ángulo inscrito, como la región sombreada en la Figura 4.3.3? En esta imagen, el centro del círculo está dentro del ángulo inscrito, y se dan las longitudes\(a \) y\(b\) de los dos acordes, al igual que el radio\(r \) del círculo. Dibujar segmentos de línea desde el centro del círculo hasta los extremos de los acordes indica cómo resolver este problema: sumar las áreas de los dos triángulos y el sector formado por el ángulo central. Las áreas y ángulos de los dos triángulos se pueden determinar (ya que se conocen los tres lados) usando métodos del Capítulo 2. También, recuerde (Teorema 2.4 en la Sección 2.5) que un ángulo central tiene el doble de la medida de cualquier ángulo inscrito que intercepte el mismo arco. En los ejercicios se te pedirá que resuelvas problemas como este (incluyendo los casos en los que el centro del círculo está afuera o en el ángulo inscrito).
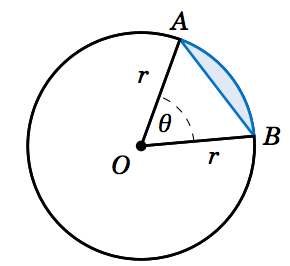
Otro tipo de región que podemos considerar es un segmento de un círculo, que es la región entre una cuerda y el arco que corta. En la Figura 4.3.4 el segmento formado por la cuerda\(\overline{AB} \) es la región sombreada entre el arco\(\overparen{AB} \) y el triángulo\(\triangle\,OAB \). Por la Ecuación 2.23 en la Sección 2.4 para el área de un triángulo dado dos lados y su ángulo incluido, sabemos que
\ [\ texto {área de}\ triángulo\, OAB ~=~\ tfrac {1} {2}\, (r)\, (r)\,\ sin\;\ theta ~=~
\ tfrac {1} {2}\, r^2\,\ sin\;\ theta ~.
\ nonumber\]
Así, dado que el área\(K \) del segmento es el área del sector\(AOB \) menos el área del triángulo\(\triangle\,OAB \), tenemos
\ [
\ text {área\(K \) de segmento} AB ~=~\ tfrac {1} {2}\, r^2\;\ theta ~-~\ tfrac {1} {2}\, r^2\,\ sin\;\ theta
~=~\ en caja {\ tfrac {1} {2}\, r^2\, (\ theta -\ sin\; theta)} ~. \ label {eqn:segmento}
\ nonumber\]
Obsérvese que como consecuencia de la Ecuación\ ref {eqn:segment} debemos tener\(\;\theta > \sin\;\theta\) for\(0 < \theta \le \pi \) (medido en radianes), ya que el área de un segmento es positiva para esos ángulos.
Encuentra el área del segmento formada por una cuerda de longitud\(3 \) en un círculo de radio\(2 \).

Figura 4.3.5
Solución
La Figura 4.3.5 muestra el segmento formado por una cuerda de longitud\(3 \) en un círculo de radio\(r=2 \). Podemos usar la Ley de Cosinos para encontrar el ángulo central subtendido\(\theta\):
\ [\ cos\;\ theta ~=~\ frac {2^2 + 2^2 - 3^2} {2\, (2)\, (2)} ~=~ -0.125\ quad\ Rightarrow
\ quad\ theta ~=~ 1.696 ~\ text {rad}
\ nonumber\]
Así, por Ecuación\ ref {eqn:segment} el área\(K \) del segmento es:
\ [K ~=~\ tfrac {1} {2}\, r^2\, (\ theta -\ sin\;\ theta) ~=~\ tfrac {1} {2}\, (2) ^2\,
(1.696 -\ sin\; 1.696) ~=~\ en caja {1.408}
\ nonumber\]
Los centros de dos círculos están separados\(7 \) cm, con un círculo que tiene un radio de\(5 \) cm y el otro un radio de\(4 \) cm. Encuentra el área\(K \) de su intersección.
Solución:
En la Figura 4.3.6 (a), vemos que la intersección de los dos círculos es la unión de los segmentos formados por la cuerda\(\overline{CD} \) en cada círculo. Así, una vez determinamos los ángulos\(\angle\,CAD \) y\(\angle\,CBD \) podemos calcular el área de cada segmento y sumar esas áreas juntas para obtener\(K \).
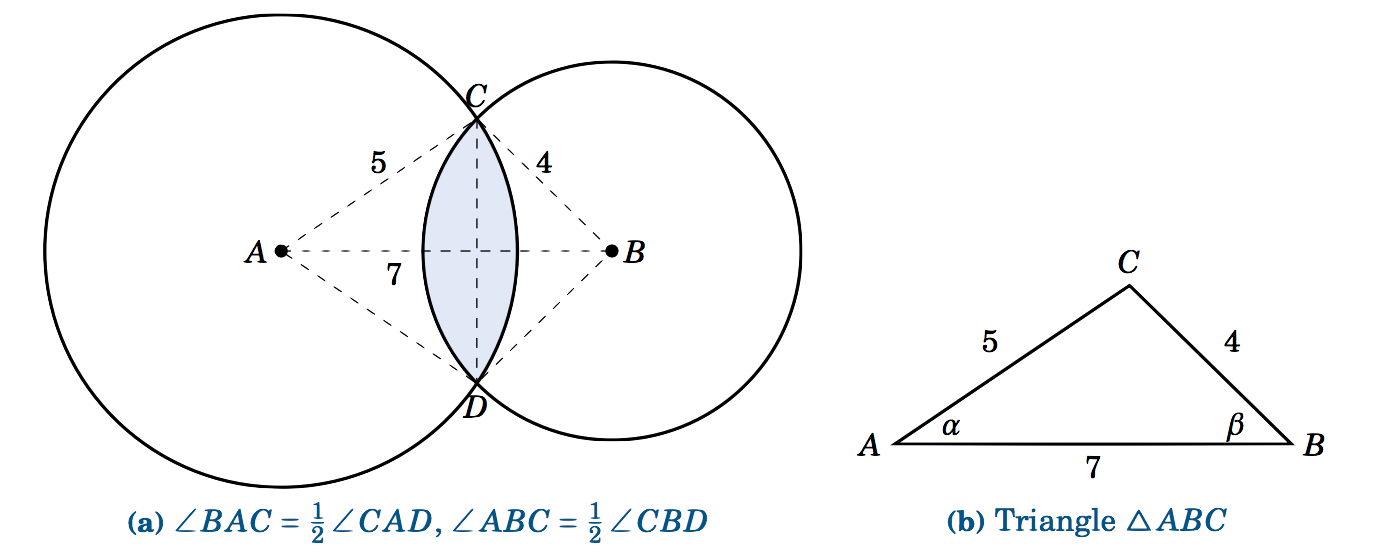
Por simetría, vemos que\(\angle\,BAC = \frac{1}{2}\,\angle\,CAD \) y\(\angle\,ABC = \frac{1}{2}\,\angle\,CBD \). Así que vamos\(\alpha = \angle\,BAC \) y\(\beta = \angle\,ABC \), como en la Figura 4.3.6 (b). Por la Ley de Cosines, tenemos
\ [\ begin {alignat*} {7}
\ cos\;\ alpha ~&=~\ frac {7^2 + 5^2 - 4^2} {2\, (7)\, (5)} ~&=~ 0.8286\ quad&\ Rightarrow\ quad
\ alpha ~&=~ 0.594~\ text {rad}\ quad&\ Rightarrow\ quad\ ángulo\ CAD ~&=~2\, (0.594) = 1.188~\ text {rad}\\\ nonúmero
\ cos\;\ beta ~&=~\ frac {7^2 + 4^2 - 5^2} {2\, (7)\, (4)} ~&=~ 0.7143\ quad&\ Rightarrow\ quad
\ beta ~&=~ 0.775~\ text {rad}\ quad&\ Rightarrow\ quad\ angle\, CBD ~&=~ 2\, (0.775) = 1.550~\ text {rad} final
\ {alignat*}\ nonumber\]
Por lo tanto, el área\(K \) es
\ [\ nonumber\ begin {align*}
K ~&=~ (\ text {Área de segmento\(CD \) en círculo en\(A\)}) ~+~
(\ text {Área de segmento\(CD \) en círculo en\(B\)})\\\ nonumber
&=~\ tfrac {1} {2}\, (5) ^2\, (1.188 -\ sin\; 1.188) ~+~\ tfrac {1} 2}\, (4) ^2\, (1.550 -\ sin \; 1.550)\\\ nonumber
&=~\ en caja {7.656~\ texto {cm} ^2} ~.
\ end {align*}\ nonumber\]


