4.2: Longitud del arco
- Page ID
- 113504
En la Sección 4.1 vimos que una revolución tiene una medida radianes de\(2\pi \) rad. Tenga en cuenta que\(2\pi\) es la relación de la circunferencia (es decir, la longitud total del arco)\(C \) de un círculo a su radio\(r\):
\ [\ text {Medida radiana de 1 revolución} ~=~ 2\ pi ~=~\ frac {2\ pi\, r} {r} ~=~
\ frac {C} {r} ~=~\ frac {\ text {longitud total del arco}} {\ text {radio}}
\ nonumber\]
Claramente, esa relación es independiente de\(r \). En general, la medida radianes de un ángulo es la relación entre la longitud del arco cortada por el ángulo central correspondiente en un círculo y el radio del círculo, independientemente del radio.
Para ver esto, recordemos nuestra definición formal de radián: el ángulo central en un círculo de radio\(r\) que intercepta un arco de longitud\(r \). Entonces supongamos que tenemos un círculo de radio\(r \) y colocamos un ángulo central con medida de radianes\(1 \) encima de otro ángulo central con medida de radianes\(1 \), como en la Figura 4.2.1 (a). Claramente, el ángulo central combinado de los dos ángulos tiene medida de radianes\(1+1=2 \), y la longitud del arco combinado es\(r+r=2r \).
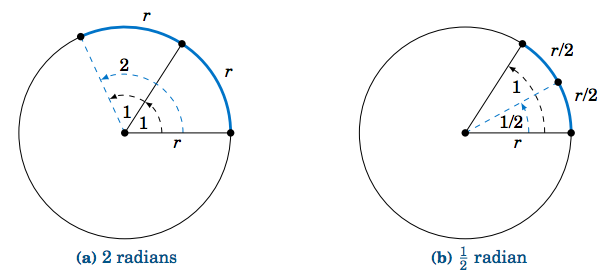
Ahora supongamos que cortamos el ángulo con medida\(1 \) de radianes a la mitad, como en la Figura 4.2.1 (b). Claramente, esto también corta la longitud del\(r \) arco a la mitad. Así, vemos que
\ [\ nonumber\ begin {align}
\ text {Ángulo} ~&=~ 1~\ texto {radián}\ quad&\ Rightarrow\ quad\ text {longitud de arco} ~&=~ r ~,\\\ nonumber
\ texto {Ángulo} ~&=~ 2~\ texto {radianes}\ cuadrados&\ Rightarrow\ quad\ text {longitud de arco} ~&=~ 2\, r ~,\\\ nonúmero
\ texto {Ángulo} ~&=~ \ tfrac {1} {2} ~\ text {radián}\ quad&\ Rightarrow\ quad\ text {longitud del arco} ~&=~
\ tfrac {1} {2}\, r ~,\ end {align}\ nonumber\]
y en general, para cualquier\(\theta \ge 0 \),
\ [\ nonumber\ text {Ángulo} ~=~\ theta~\ texto {radianes}\ quad\ Rightarrow\ quad\ text {longitud de arco} ~=~\ theta\, r ~,
\ nonumber\]
para que
\ [\ theta ~=~\ frac {\ text {longitud del arco}} {\ texto {radio}} ~~.
\ nonumber\]
Intuitivamente, es obvio que al encoger o magnificar un círculo se preserva la medida de un ángulo central incluso cuando cambia el radio. La discusión anterior dice más, a saber, que se conserva la relación entre la longitud\(s \) de un arco interceptado y el radio\(r \), precisamente porque esa relación es la medida del ángulo central en radianes (ver Figura 4.2.2).
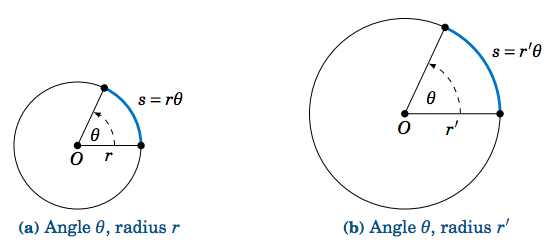
Así obtenemos una fórmula simple para la longitud de un arco:
En un círculo de radio\(r \), deja\(s \) ser la longitud de un arco interceptado por un ángulo central con medida de radianes\(\theta \ge 0 \). Entonces la longitud del arco\(s \) es:
\[ s ~=~ r\,\theta \label{4.4} \]
En un círculo de radio\(r=2 \) cm, ¿cuál es la longitud\(s \) del arco interceptado por un ángulo central de medida\(\theta = 1.2 \) rad?
Solución
Usando la ecuación\ ref {4.4}, obtenemos:
\[s ~=~ r\,\theta ~=~ (2)\,(1.2) ~=~ \boxed{2.4~\text{cm}} \nonumber \]
En un círculo de radio\(r=10 \) ft, ¿cuál es la longitud\(s \) del arco interceptada por un ángulo central de medida\(\theta = 41^\circ\;\)?
Solución
Usando la Ecuación\ ref {4.4} ciegamente con\(\theta = 41^\circ \), obtendríamos\(\;s = r\,\theta = (10)\,(41) = 410 \) ft. Pero esto imposible, ya que un círculo de radio\(10 \) ft tiene una circunferencia de solo\(2\pi\,(10) \approx 62.83 \) ft! Nuestro error fue en usar el ángulo\(\theta \) medido en grados, no radianes. Entonces primero convierte\(\theta =41^\circ \) a radianes, luego usa\(s=r\,\theta\):
\ [\ theta = 41^\ circ ~=~\ frac {\ pi} {180}\;\ cdot\; 41 ~=~ 0.716~\ text {rad}
\ quad\ Rightarrow\ quad s ~=~ r\,\ theta ~=~ (10)\, (0.716) ~=~\ en caja {7.16~\ texto {ft}}\ nonumber\]
Tenga en cuenta que dado que la longitud del arco\(s \) y el radio generalmente\(r \) se dan en las mismas unidades, la medida del radián es realmente sin unidades, ya que se puede pensar en las unidades cancelando en la relación\(\frac{s}{r} \), que es justa\(\theta \). Esta es otra razón por la que los radianes son tan ampliamente utilizados.
Un ángulo central en un círculo de radio\(5 \) m corta un arco de longitud\(2 \) m. ¿Cuál es la medida del ángulo en radianes? ¿Cuál es la medida en grados?
Solución
Dejando\(r=5 \) y\(s=2 \) en la Ecuación\ ref {4.4}, obtenemos:
\[\theta ~=~ \frac{s}{r} ~=~ \frac{2}{5} ~=~ \boxed{0.4~\text{rad}}\nonumber \]
En grados, el ángulo es:
\[ \theta = 0.4~\text{rad} ~=~ \frac{180}{\pi} \;\cdot\; 0.4 ~=~ \boxed{22.92^\circ}\nonumber \]
Para los ángulos centrales\(\theta > 2\pi \) rad, es decir\(\theta > 360^\circ \), puede que no quede claro qué se entiende por arco interceptado, ya que el ángulo es mayor que una revolución y por lo tanto “envuelve” el círculo más de una vez. Tomaremos el enfoque de que dicho arco consiste en la circunferencia completa más cualquier longitud de arco adicional determinada por el ángulo. En otras palabras, la Ecuación\ ref {4.4} sigue siendo válida para ángulos\(\theta > 2\pi \) rad.
¿Qué pasa con los ángulos negativos? En este caso el uso\(s=r\,\theta \) significaría que la longitud del arco es negativa, lo que viola el concepto habitual de longitud. Por lo que vamos a adoptar la convención de utilizar únicamente ángulos centrales no negativos al discutir la longitud del arco.
Una cuerda se sujeta a una pared en dos lugares a\(8 \) pies de distancia a la misma altura. Un contenedor cilíndrico con un radio de\(2 \) pies es empujado lejos de la pared hasta donde puede llegar mientras está sujeto por la cuerda, como en la Figura 4.2.3 que muestra la vista superior. Si el centro del contenedor está a\(3 \) pies del punto en la pared a medio camino entre los extremos de la cuerda, ¿cuál es la longitud\(L \) de la cuerda?
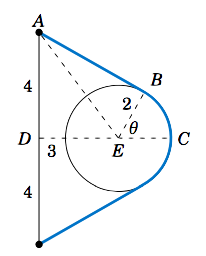
Solución:
Vemos que, por simetría, la longitud total de la cuerda es\(\;L = 2\;(AB + \overparen{BC}) \). También, observe que\(\triangle\,ADE \) es un triángulo rectángulo, por lo que la hipotenusa tiene longitud\(AE = \sqrt{DE^2 + DA^2} = \sqrt{3^2 + 4^2} = 5 \) ft, según el Teorema de Pitágoras. Ahora como\(\overline{AB} \) es tangente al contenedor circular, sabemos que\(\angle\,ABE \) es un ángulo recto. Así que por el Teorema de Pitágoras tenemos
\[ AB ~=~ \sqrt{AE^2 - BE^2} ~=~ \sqrt{5^2 - 2^2} ~=~ \sqrt{21} ~\text{ft}. \nonumber \]
Por Ecuación\ ref {4.4} el arco\(\overparen{BC} \) tiene longitud\(BE \cdot \theta \), donde\(\theta = \angle\,BEC \) está el suplemento de\(\angle\,AED + \angle\,AEB \). Así que desde
\ [\ tan\,\ ángulo\, DEA ~=~\ frac {4} {3} ~\ Derecha~\ ángulo\, AED ~=~ 53.1^\ circ\ quad\ texto {y}
\ quad\ cos\,\ ángulo\, AEB ~=~\ frac {BE} {AE} ~=~\ frac {2} {5} ~\ ángulo\, AEB ~=~ 66.4^\ circ ~,
\ nonumber\]
tenemos
\ [\ nonumber
\ theta ~=~\ ángulo\, BEC ~=~ 180^\ circ\; -\; (\ ángulo\, AED +\ ángulo\, AEB) ~=~ 180^\ circ\; -\;
(53.1^\ circ + 66.4^\ circ) ~=~ 60,5^\ circ ~.
\ nonumber\]
Convertiéndonos a radianes, obtenemos\(\;\theta = \frac{\pi}{180} \;\cdot\; 60.5 = 1.06 \) rad. Así,
\ [L ~=~ 2\, (AB\; +\;\ cdot\ overparen {BC}) ~=~ 2\, (\ sqrt {21}\; +\; BE\ cdot\ theta) ~=~
2\, (\ sqrt {21}\; +\; (2)\, (1.06)) ~=~\ en caja {13.4 ~\ texto ft}} ~.
\ nonumber\]
Los centros de dos poleas de correa, con radios de\(5 \) cm y\(8 \) cm, respectivamente, están separados por\(15 \) cm. Encuentra la longitud total\(L \) de la correa alrededor de las poleas.
Solución
En la Figura 4.2.4 vemos que, por simetría,\(\;L = 2\;(\overparen{DE} + EF + \overparen{FG}) \).
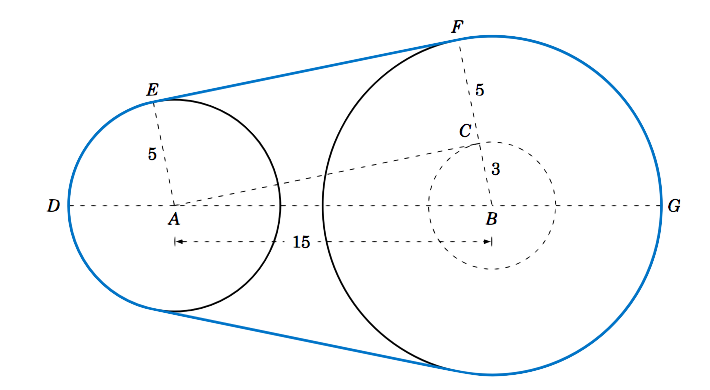
Primero, en el centro\(B \) de la polea con radio\(8 \), dibuja un círculo de radio\(3 \), que es la diferencia en los radios de las dos poleas. \(C \)Sea el punto donde este círculo se cruza\(\overline{BF} \). Entonces sabemos que la línea tangente\(\overline{AC} \) a este círculo más pequeño es perpendicular al segmento de línea\(\overline{BF} \). Por lo tanto,\(\angle\,ACB \) es un ángulo recto, y así la longitud de\(\overline{AC} \) es
\[AC ~=~ \sqrt{AB^2 - BC^2} ~=~ \sqrt{15^2 - 3^2} ~=~ \sqrt{216} ~=~ 6\,\sqrt{6}\nonumber \]
por el Teorema de Pitágoras. Ahora desde\(\overline{AE} \perp \overline{EF} \) y\(\overline{EF} \perp \overline{CF} \) y\(\overline{CF} \perp \overline{AC} \), el cuadrilátero\(AEFC \) debe ser un rectángulo. En particular,\(EF = AC \), entonces\(EF = 6\,\sqrt{6} \).
Por Ecuación\ ref {4.4} sabemos eso\(\;\overparen{DE} = EA \cdot \angle\,DAE\; \) y\(\;\overparen{FG} = BF \cdot \angle\,GBF \), donde los ángulos se miden en radianes. Así que pensando en ángulos en radianes (usando\(\pi \) rad\(= 180^\circ\)), vemos en la Figura 4.2.4 que
\ [\ nonumber\ ángulo\, DAE ~=~\ pi\; -\;\ ángulo\, EAC\; -\;\ ángulo\, BAC ~=~\ pi\; -\ frac {\ pi} {2}\; -\ ángulo\, BAC ~=~\ frac {
\ pi} {2}\; -\ ángulo\, BAC ~,\ nonumber\, BAC ~,\ nonumber\, BAC ~,\ umber\]
donde
\ [\ nonumber\ sin\;\ ángulo\, BAC ~=~\ frac {BC} {AB} ~=~\ frac {3} {15} ~=~ 0.2\ quad\ Rightarrow\ quad\ quad
\ ángulo\, BAC ~=~ 0.201~\ text {rad.} \ nonumber\]
Así,\(\;\angle\,DAE = \frac{\pi}{2} \,-\, 0.201 = 1.37 \) rad. Entonces desde\(\overline{AE} \) y\(\overline{BF} \) son paralelos, tenemos\(\;\angle\,ABC = \angle\,DAE = 1.37 \) rad. Así,\(\;\angle\,GBF = \pi \,-\, \angle\,ABC = \pi \,-\, 1.37 = 1.77 \) rad. De ahí que,
\ [\ nonumber L ~=~ 2\; (\ overparen {DE}\; +\; EF\; +\;\ overparen {FG}) ~=~ 2\; (5\; (1.37)\; +\; 6\,\ sqrt {6}\; +\;
8\ ;( 1.77)) ~=~\ en caja {71.41~\ texto cm}} ~. \ nonumber\]


