4.4: Movimiento Circular- Velocidad Lineal y Angular
- Page ID
- 113505
La medida de radianes y la longitud del arco se pueden aplicar al estudio del movimiento circular. En física la velocidad promedio de un objeto se define como:
\ [\ text {velocidad media} ~=~\ frac {\ text {distancia recorrida}} {\ texto {tiempo transcurrido}}
\ nonumber\]
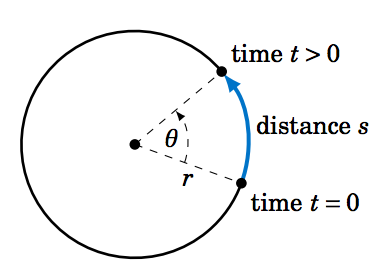
Entonces supongamos que un objeto se mueve a lo largo de un círculo de radio\(r \), recorriendo una distancia a\(s \) lo largo de un periodo de tiempo\(t \), como en la Figura 4.4.1. Entonces tiene sentido definir la velocidad lineal (promedio)\(\nu \) del objeto como:
\[ \nu ~=~ \frac{s}{t}\label{eqn:linspeed} \]
\(\theta \)Sea el ángulo barrido por el objeto en ese periodo de tiempo. Luego definimos la velocidad angular (promedio)\(\omega \) del objeto como:
\[ \omega ~=~ \frac{\theta}{t}\label{eqn:angspeed} \]
La velocidad angular da la velocidad a la que el ángulo central barrido por el objeto cambia a medida que el objeto se mueve alrededor del círculo y, por lo tanto, se mide en radianes por unidad de tiempo. La velocidad lineal se mide en unidades de distancia por unidad de tiempo (por ejemplo, pies por segundo). La palabra lineal se usa porque enderezar el arco recorrido por el objeto a lo largo del círculo da como resultado una línea de la misma longitud, de manera que se puede usar la definición habitual de velocidad como distancia en el tiempo. Por lo general omitiremos la palabra promedio al discutir aquí la velocidad lineal y angular.
Dado que la longitud\(s \) del arco cortado por un ángulo central\(\theta \) en un círculo de radio\(r \) es\(s=r\,\theta \), vemos que
\ [\ nu ~=~\ frac {s} {t} ~=~\ frac {r\,\ theta} {t} ~=~\ frac {\ theta} {t}\;\ cdot\; r ~,
\ nonumber\]
para que obtengamos la siguiente relación entre velocidad lineal y angular:
\[ \nu ~=~ \omega\,r\label{eqn:linang} \]
Un objeto barre un ángulo central de\(\frac{\pi}{3} \) radianes en\(0.5 \) segundos a medida que se mueve a lo largo de un círculo de radio\(3 \) m. Encuentra su velocidad lineal y angular durante ese período de tiempo.
Solución:
Aquí tenemos\(t=0.5 \) sec,\(r=3 \) m, y\(\theta = \frac{\pi}{3} \) rad. Entonces la velocidad angular\(\omega \) es
\ [\ omega ~=~\ frac {\ theta} {t} ~=~\ frac {\ dfrac {\ pi} {3} ~\ text {rad}} {0.5~\ text {seg}}
\ quad\ Rightarrow\ quad\ en caja {\ omega ~=~\ frac {2\ pi} {3} ~\ texto {rad/seg}} ~,
no umbumbra er\]
y por lo tanto la velocidad lineal\(\nu \) es
\ [\ nu ~=~\ omega\, r ~=~\ izquierda (\ frac {2\ pi} {3} ~\ texto {rad/seg}\ derecha)\, (3~\ texto {m})
\ quad\ Rightarrow\ quad\ boxed {\ nu ~=~ 2\ pi~\ text {m/seg}} ~.
\ nonumber\] Tenga en cuenta que las unidades para\(\omega \) son rad/seg y las unidades de\(\nu \) son m/seg. Recordemos que los radianes en realidad no tienen unidades, razón por la cual en la Ecuación\(\nu=\omega\,r \) las unidades de radianes desaparecen.
Un objeto recorre una distancia de\(35 \) pies en\(2.7 \) segundos a medida que se mueve a lo largo de un círculo de radio\(2 \) ft. Encuentra su velocidad lineal y angular durante ese periodo de tiempo.
Solución:
Aquí tenemos\(t=2.7 \) sec,\(r=2 \) ft y\(s=35 \) ft. Entonces la velocidad lineal\(\nu \) es
\ [\ nu ~=~\ frac {s} {t} ~=~\ frac {35~\ texto {pies}} {2.7~\ texto {seg}}\ quad\ Rightarrow\ quad
\ en caja {\ nu ~=~ 12.96~\ texto {pies/seg}} ~,
\ nonumber\]
y así la velocidad angular\(\omega \) viene dada por
\ [\ nonumber
\ nu ~=~\ omega\, r\ quad\ Rightarrow\ quad 12.96~\ text {ft/seg} ~=~\ omega\, (2~\ text {ft})
\ quad\ Rightarrow\ quad\ boxed {\ omega ~=~ 6.48~\ text {rad/seg}} ~.
\ nonumber\]
Un objeto se mueve a una velocidad lineal constante de\(10 \) m/seg alrededor de un círculo de radio\(4 \) m. ¿Qué tan grande de un ángulo central barre en\(3.1 \) segundos?
Solución:
Aquí tenemos\(t=3.1 \) sec,\(\nu=10 \) m/seg, y\(r=4 \) m. Así, el ángulo\(\theta \) viene dado por
\ [s ~=~ r\,\ theta\ quad\ Rightarrow\ quad\ theta ~=~\ frac {s} {r} ~=~\ frac {\ nu\, t} {r} ~=~
\ frac {(10~\ text {m/seg})\, (3.1~\ text {seg})} {4~\ text {m}} ~=~\ en caja {7.75~\ texto {rad}} ~.
\ nonumber\]
En muchas aplicaciones físicas la velocidad angular se da en revoluciones por minuto, abreviada como rpm. Para convertir de rpm a, digamos, radianes por segundo, observe que como hay\(2\pi \) radianes en una revolución y\(60 \) segundos en un minuto, podemos convertir\(N \) rpm en radianes por segundo “cancelando las unidades” de la siguiente manera:
\ [\ require {cancel}\ nonumber
N~\ text {rpm} ~=~ N~\ frac {\ cancel {\ text {rev}}} {\ cancel {\ text {min}}\;\ cdot\;
\ frac {2\ pi~\ text {rad}} {1~\ cancel {\ text {rev}}
\;\ cdot\;\ frac {1~ ~\ cancel {\ texto {min}}} {60~\ texto {seg}} ~=~\ frac {N\ cdot 2\ pi} {60} ~\ texto {rad/seg}
\ nonumber\]
Esto funciona porque todo lo que hicimos fue multiplicar por\(1 \) dos veces. La conversión a otras unidades para velocidad angular funciona de manera similar. Yendo en sentido contrario, digamos, de rad/seg a rpm, da:
\ [N~\ texto {rad/seg} ~=~\ frac {N\ cdot 60} {2\ pi} ~\ texto {rpm}
\ nonumber\]
Un engranaje con un radio exterior de\(r_1 = 5 \) cm se mueve en el sentido de las agujas del reloj, haciendo que un engranaje de enclavamiento con un radio exterior de\(r_2 = 4 \) cm se mueva en sentido contrario a las agujas del reloj a una velocidad angular de\(\omega_2 = 25 \) rpm. ¿Cuál es la velocidad angular\(\omega_1 \) del engranaje más grande?
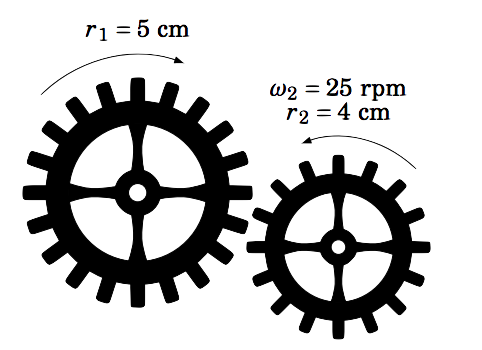
Figura 4.4.2
Solución:
Imagina una partícula en el radio exterior de cada engranaje. Después de que los engranajes hayan girado por un periodo de tiempo\(t>0 \), el desplazamiento circular de cada partícula será el mismo. En otras palabras,\(s_1 = s_2 \), dónde\(s_1 \) y\(s_2 \) son las distancias recorridas por las partículas en los engranajes con radios\(r_1 \) y\(r_2 \), respectivamente.
Pero\(s_1 = \nu_1 \,t \) y\(s_2 = \nu_2 \,t \), donde\(\nu_1 \) y\(\nu_2 \) son las velocidades lineales de los engranajes con radios\(r_1 \) y\(r_2 \), respectivamente. Por lo tanto,
\ [\ nu_1\, t =\ nu_2\, t\ quad\ Rightarrow\ quad\ nu_1 =\ nu_2 ~,
\ nonumber\]
así que por Ecuación\ ref {eqn:linang} obtenemos la relación fundamental entre los dos engranajes:
\ [
\ en caja {\ omega_1\, r_1 ~=~\ omega_2\, r_2}\ etiqueta {eqn:engranajes}
\ nonumber\]
Tenga en cuenta que esto se mantiene para dos engranajes cualesquiera. Así que en nuestro caso, tenemos
\ [\ omega_1\, (5) ~=~ (25)\, (4)\ quad\ Rightarrow\ quad\ en caja {\ omega_1 ~=~ 20~\ texto {rpm}} ~.
\ nonumber\]


