6.2: Métodos numéricos en trigonometría

Pudimos resolver las ecuaciones trigonométricas de la sección anterior con bastante facilidad, lo que en general no es el caso. Por ejemplo, considere la ecuación

\ [\ label {eqn:cosinefixed}
\ cos\; x ~=~ x ~.
\ nonumber\]

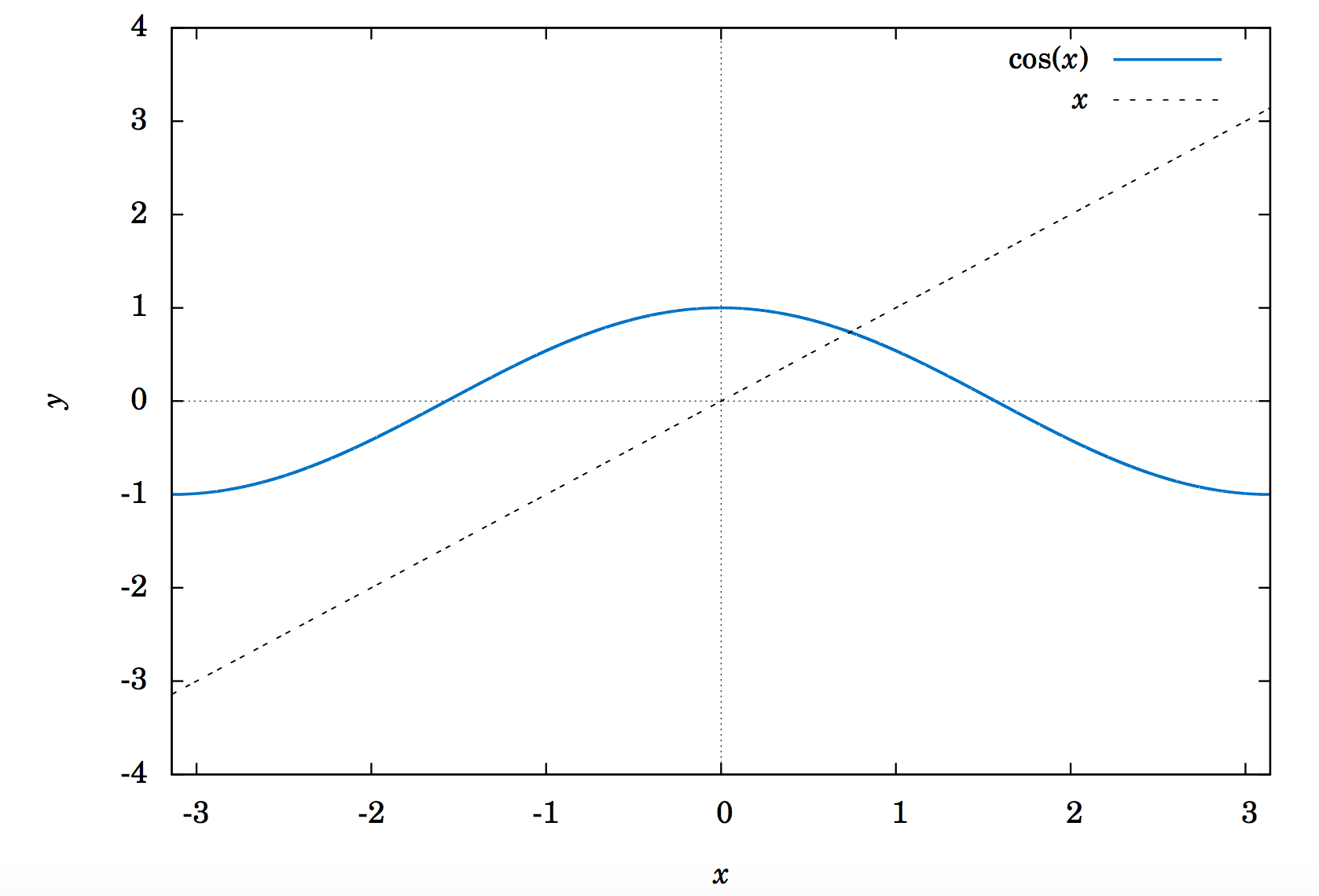
Existe una solución, como se muestra en la Figura 6.2.1 a continuación. Las gráficas de\(y=\cos\;x\) y se\(y=x \) cruzan en algún lugar entre\(x=0 \) y\(x=1 \), lo que significa que hay una\(x \) en el intervalo\([0,1\ \) tal que\(\cos\;x = x \).

Figura 6.2.1\(y = \cos x \text{ and }y = x\)

Desafortunadamente no existe una identidad trigonométrica ni un método simple que nos ayude aquí. En cambio, tenemos que recurrir a métodos numéricos, que proporcionan formas de obtener sucesivamente mejores aproximaciones a la (s) solución (s) real (s) dentro de cualquier grado de precisión deseado. Existe un amplio campo de las matemáticas dedicado a este tema llamado análisis numérico. Muchos de los métodos requieren cálculo, pero afortunadamente hay un método que podemos usar que requiere solo álgebra básica. Se llama el método secante, y encuentra raíces de una función dada\(f(x) \), es decir, valores de\(x \) tal que\(f(x)=0 \). Una derivación del método secante está más allá del alcance de este libro, pero podemos afirmar el algoritmo que utiliza para resolver\(f(x)=0\):

1. Elija puntos iniciales\(x_0 \) y\(x_1 \) tal que\(x_0 < x_1 \) y\(f(x_0)\,f(x_1) < 0 \) (es decir,
   la solución está en algún lugar entre\(x_0 \) y\(x_1\)).
2. Para\(n \ge 2 \), defina el número\(x_n \) por

   \ [\ label {eqn:secantmethod}
   x_n ~=~ x_ {n-1} ~-~\ dfrac {(x_ {n-1}\; -\; x_ {n-2})\, f (x_ {n-1})} {f (x_ {n-1})\; -\; f (x_ {n-2})}
   \ nonumber\]

   siempre y cuando\(|x_{n-1} \;-\; x_{n-2}| > \epsilon_{error} \), donde\(\epsilon_{error} > 0 \) está la cantidad máxima de error deseada (generalmente un número muy pequeño).

3. Los números\(x_0 \),,\(x_1 \),\(x_2 \),\(x_3 \),\(... \) se acercarán a la solución a\(x \) medida que vayamos atravesando más iteraciones, acercándonos lo más deseado.

Ahora vamos a mostrar cómo usar este algoritmo para resolver la ecuación\(\cos\;x = x \). La solución a esa ecuación es la raíz de la función\(f(x) =\cos\;x - x \). Y vimos que la solución está en algún lugar del intervalo\([0,1] \). Así que elige\(x_0 = 0 \) y\(x_1 = 1 \). Entonces\(f(0)=1 \) y\(f(1)=-0.4597 \), para eso\(f(x_0)\,f(x_1) < 0 \) (estamos usando radianes, claro). Entonces por definición,

\ [\ nonumber\ begin {align*}
x_2 ~&=~ x_1 ~-~\ dfrac {(x_1\; -\; x_0)\, f (x_1)} {f (x_1)\; -\; f (x_0)}\\\ nonumber
&=~ 1 ~-~\ dfrac {(1\; -\; 0)\, f (1)} {f (1)\; -\; f (0)}\\\ nonúmero
&=~ 1 ~-~\ dfrac {(1\; -\; 0)\, (-0.4597)} {-0.4597\; -\; 1}\\\ nonumber
&=~ 0.6851~,\\ nonumber
x_3 ~&=~ x_2 ~-~\ dfrac {(x_2\; -\; x_1)\, f (x_2)} {f (x_2)\; -\; f (x_1)}\\\ nonumber
&=~ 0.6851 ~-~\ dfrac {(0.6851\; -\; 1)\, f (0.6851)} {f (0.6851)\; -\; f (1)}\\\ nonumber
&=~ 0.6851 ~-~\ dfrac {(0.6851\; -\; 1)\, (0.0893)} {0.0893 \; -\; (-0.4597)}\\\ nonumber
&=~ 0.7363 ~,
\ end {align*}\ nonumber\]

y así sucesivamente. El uso de una calculadora no es muy eficiente y dará lugar a errores de redondeo. Una mejor manera de implementar el algoritmo es con una computadora. El listado 6.1 a continuación muestra el código (secant.java) para resolver\(\cos\;x = x \) con el método secante, usando el lenguaje de programación Java:

Listado 6.1 Listado de programas para secant.java

Las líneas 4-5 leen en\(x_0 \) y\(x_1 \) como parámetros de entrada al programa.
La línea 6 inicializa la variable que eventualmente mantendrá la solución.
La línea 7 establece que el error máximo\(\epsilon_{error} \) sea\(1.0 \,\times\, 10^{-50} \). Es decir, nuestra respuesta final estará dentro de eso (¡pequeña!) cantidad de la solución real.
La línea 8 inicia un bucle de 9 iteraciones del algoritmo, es decir, creará las aproximaciones sucesivas\(x_2 \),\(x_3 \),\(... \),\(x_{10} \) a la solución real, aunque en la Línea 9 comprobamos para ver si las dos aproximaciones anteriores difieren en menos del error máximo. Si lo hacen, nos detenemos (ya que esto significa que tenemos una solución aceptable), de lo contrario continuamos.
La línea 10 es el paso principal en el algoritmo, creando\(x_n \) desde\(x_{n-1} \) y\(x_{n-2} \).
Las líneas 11-12 establecen los nuevos valores de\(x_{n-2} \) y\(x_{n-1} \), respectivamente.
Las líneas 18-20 establecen el número de decimales que se mostrarán en la respuesta final en 50 (el valor predeterminado es 16) y luego imprimen la respuesta.
Las líneas 23-24 dan la definición de la función\(f(x)=\cos\;x - x \).

A continuación se muestra el resultado de compilar y ejecutar el programa usando\(x_0 = 0 \) y\(x_1 = 1\):

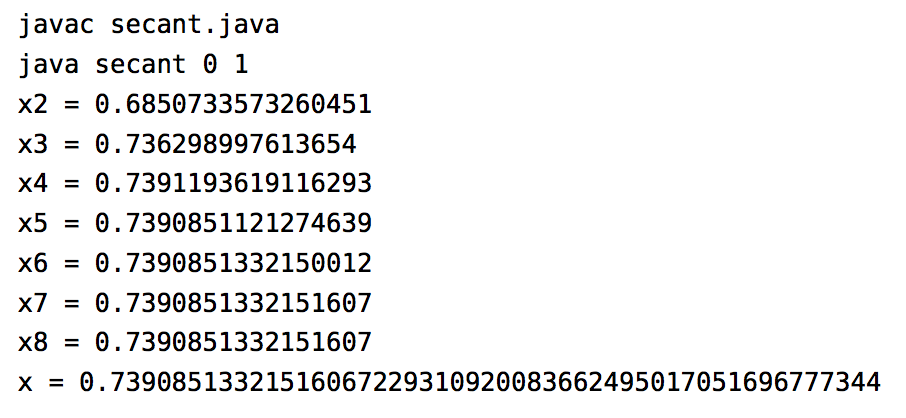
Observe que el programa sólo se levantó\(x_8 \), no\(x_{10} \). La razón es que la diferencia entre\(x_8 \) y\(x_7 \) era lo suficientemente pequeña (menos que\(\epsilon_{error} = 1.0 \,\times\, 10^{-50}\)) como para detenerse\(x_8 \) y llamar a eso nuestra solución. La última línea muestra esa solución a 50 decimales.

¿Ese número le resulta familiar? Debería, ya que es la respuesta al Ejercicio 11 en la Sección 4.1. Es decir, al tomar cosenos repetidos comenzando con cualquier número (en radianes), eventualmente comienzas a obtener el número anterior repetidamente después de suficientes iteraciones. Esto resulta no ser una coincidencia. La figura 6.2.2 da una idea de por qué.

Figura 6.2.2 Punto fijo atractivo para\(\cos x\)

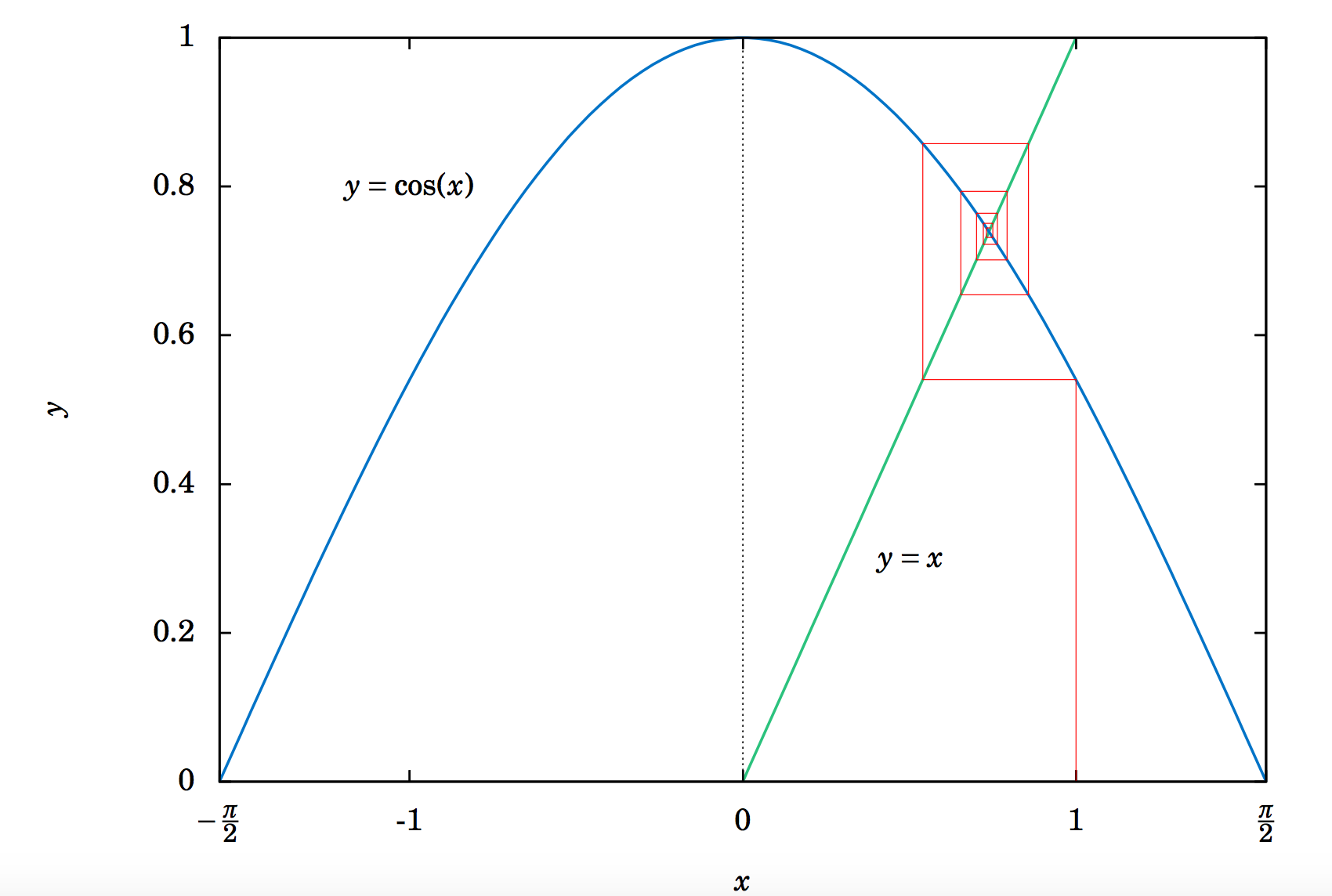
Ya que\(x=0.73908513321516... \) es la solución de\(\cos\;x = x \), se obtendría\(\cos\;(\cos\;x) = \cos\;x = x \), así\(\cos\;(\cos\;(\cos\;x)) = \cos\;x = x \), y así sucesivamente. A este número\(x \) se le llama un punto fijo atractivo de la función\(\cos\;x \). No importa por donde empieces, terminas siendo ``dibujado” a ello. La Figura 6.2.2 muestra lo que sucede al comenzar en\(x=0\): tomar el coseno de te\(0 \) lleva a\(1 \), y luego cosenos sucesivos (indicados por las intersecciones de las líneas verticales con la curva del coseno) eventualmente “espiral” de manera rectangular al punto fijo (es decir, la solución), que es la intersección de\(y=\cos\;x\) y\(y=x \).

Recordemos en el Ejemplo 5.10 en la Sección 5.2 que afirmamos que el máximo y el mínimo de la función\(y=\cos\;6x + \sin\;4x \) fueron\(\pm\,1.90596111871578 \), respectivamente. Podemos mostrar esto usando el programa de código abierto Octave. Octave utiliza un método de programación cuadrática sucesiva para encontrar el mínimo de una función\(f(x) \). Encontrar el máximo de\(f(x) \) es lo mismo que encontrar el mínimo de\(-f(x) \) luego multiplicar por\(-1 \) (¿por qué?). A continuación te mostramos los comandos para ejecutar en el símbolo del sistema Octave (\(\texttt{octave:n>}\)) para encontrar el mínimo de\(f(x) = \cos\;6x + \sin\;4x \). El comando\(\texttt{sqp(3,'f')}\) dice usar\(x=3 \) como primera aproximación del número\(x \) donde\(f(x) \) es un mínimo.

El resultado dice que el mínimo ocurre cuando\(x=2.65792064609274 \) y que el mínimo es\(-1.90596111871578 \). Para encontrar el máximo de\(f(x) \), encontramos el mínimo de\(-f(x) \) y luego tomamos su negativo. El comando\(\texttt{sqp(2,'f')}\) dice usar\(x=2 \) como primera aproximación del número\(x \) donde\(f(x) \) es un máximo.

El resultado dice que el máximo ocurre cuando\(x=2.05446832062993\) y que el máximo es\(-(-1.90596111871578) = 1.90596111871578 \).

Recordemos de la Sección 2.4 que la fórmula de Heron es adecuada para triángulos “típicos”, pero a menudo tendrá un problema cuando se usa en una calculadora con, digamos, un triángulo con dos lados cuya suma es apenas mayor que la tercera cara. Sin embargo, se puede sortear este problema mediante el uso de software de computadora capaz de manejar números con un alto grado de precisión. La mayoría de los lenguajes de programación informática modernos tienen esta capacidad. Por ejemplo, en el lenguaje de programación Python (elegido aquí por simplicidad) el\(\texttt{decimal}\) módulo se puede utilizar para establecer cualquier nivel de precisión. A continuación mostramos cómo obtener precisión hasta\(50 \) decimales usando la fórmula de Heron para el triángulo en el Ejemplo 2.16 de la Sección 2.4, mediante el uso del shell de comandos interactivo python:

(Nota: La flecha triple\(>>>\) es solo un símbolo del sistema, no parte del código). Observe en este caso que sí obtenemos la respuesta correcta; el alto nivel de precisión elimina los errores de
redondeo que muestran muchas calculadoras al usar la fórmula de Heron.

Otra opción de software es Sage, un potente y gratuito paquete de matemáticas de código abierto basado en Python. Se puede ejecutar en su propia computadora, pero también se puede ejecutar a través de una interfaz web: vaya a http://sagenb.org para crear una cuenta gratuita, luego una vez que se registre e inicie sesión, haga clic en el enlace Nueva hoja de trabajo para comenzar a ingresar comandos. Por ejemplo, para encontrar la solución a\(\cos\;x = x \) en el intervalo\([0,1] \), ingrese estos comandos en el campo de texto de la hoja de trabajo:

Haga clic en el enlace evaluar para mostrar la respuesta:\(0.7390851332151559\)