6.3: Números complejos
- Page ID
- 113560
No hay un número real\(x \) tal que\(x^2 = -1 \). No obstante, resulta útil inventar tal número, llamado unidad imaginaria y denotado por la letra\(i \). Así,\(i^2 = -1 \), y por lo tanto\(i = \sqrt{-1} \). Si\(a \) y\(b \) son números reales, entonces un número de la forma\(a + bi \) se llama un número complejo, y si\(b \ne 0 \) entonces se llama un número imaginario (y puro imaginario si\(a=0 \) y\(b \ne 0\)). El número real\(a \) se llama la parte real del número complejo\(a+bi \), y\(bi \) se llama su parte imaginaria.
¿Qué significa\(a \) sumar\(bi \) en la definición\(a+bi \) de un número complejo, es decir, sumar un número real y un número imaginario? Se puede pensar en ello como una forma de extender el conjunto de números reales. Si\(b=0 \) entonces\(a+bi = a+0i = a \) (ya que\(0i \) se define como\(0\)), de modo que cada número real es un número complejo. La parte imaginaria\(bi \) en\(a+bi \) puede pensarse como una forma de tomar el conjunto unidimensional de todos los números reales y extenderlo a un conjunto bidimensional: hay una correspondencia natural entre un número complejo\(a+bi \) y un punto\((a,b) \) en el plano\(xy\) coordenado (bidimensional).
Antes de explorar más a fondo esa correspondencia, primero expondremos algunas propiedades fundamentales y operaciones en números complejos:
Dejar\(a+bi \) y\(c+di \) ser números complejos. Entonces:
- \(a+bi ~=~ c+di \)si y solo si\(a=c \) y\(b=d~ \) (es decir, las partes reales son iguales y las partes imaginarias son iguales)
- \((a+bi) \;+\; (c+di) ~=~ (a+c) \;+\; (b+d)i~ \)(es decir, sumar las partes reales y sumar las partes imaginarias juntas)
- \((a+bi) \;-\; (c+di) ~=~ (a-c) \;+\; (b-d)i\)
- \((a+bi)\,(c+di) ~=~ (ac-bd) \;+\; (ad+bc)i\)
- \((a+bi)\,(a-bi) ~=~ a^2 \;+\; b^2\)
- \(\dfrac{a+bi}{c+di} ~=~ \dfrac{(ac+bd) \;+\; (bc-ad)i}{c^2 + d^2}\)
Los tres primeros ítems anteriores son solo definiciones de igualdad, suma y resta de números complejos. Los tres últimos ítems se pueden derivar tratando la multiplicación y división de números complejos como normalmente trataría factores de números reales:
\ [\ nonumber\ begin {alinear*}
(a+bi)\, (c+di) ~&=~ a\, (c+di)\; +\; bi\, (c+di)\\\ nonumber
&=~ ac\; +\; adi\; +\; bci\; +\; bdi^2 ~=~ ac\; +\; adi\; +\; bci\; +\; bd (-1)\\\ nonumber
&=~ (ac - bd)\; +\; (ad+bc) i
\ end {align*}\ nonumber\]
El quinto ítem es un caso especial de la fórmula de multiplicación:
\ [\ nonumber\ begin {align*}
(a+bi)\, (a-bi) ~&=~ ((a) (a) - (b) (-b))\; +\; ((a) (-b) + (b) (a)) i\\ nonumber
&=~ (a^2 + b^2)\; +\; (-ab ba +) i ~=~ (a^2 + b^2)\; +\; 0i\\\ nonumber
&=~ a^2\; +\; b^2
\ end {align*}\ nonumber\]
El sexto ítem proviene del uso de los ítems anteriores:
\ [\ nonumber\ begin {align*}
\ dfrac {a+bi} {c+di} ~&=~\ dfrac {a+bi} {c+di}\,\ cdot\,\ dfrac {c-di} {c-di}\\\ nonumber
&=~\ dfrac {(ac - b (-d))\; +\; (a (-d) + bc) i} {c^2 + d^2}\\\ nonumber
&=~\ dfrac {(ac+bd)\; +\; (bc-ad) i} {c^2 + d^2}
\ end {alinear*}\ nonumber\]
El conjugado\(\overline{a+bi} \) de un número complejo\(a+bi \) se define como\(\overline{a+bi} = a-bi \). Observe que\((a+bi) \;+\; \overline{(a+bi)} ~=~ 2a \) es un número real,\((a+bi) \;-\; \overline{(a+bi)} ~=~ 2bi \) es un número imaginario si\(b \ne 0 \), y\((a+bi) \overline{(a+bi)} ~=~ a^2 + b^2 \) es un número real. Entonces para un número complejo\(z=a+bi \),\(z\,\overline{z} = a^2 + b^2 \, \) y así podemos definir el módulo de\(z\) ser\(\sqrt{z\,\overline{z}} = \sqrt{a^2 + b^2} \), que denotamos por\(|z| \).
Dejar\(z_1 = -2+3i \) y\(z_2 = 3+4i \). Encontrar\(z_1 + z_2 \),\(z_1 - z_2 \),\(z_1 \, z_2 \),\(z_1 / z_2 \),\(|z_1| \), y\(|z_2| \).
Solución
Usando nuestras reglas y definiciones, tenemos:
\ [\ nonumber\ begin {alinear*}
z_1\; +\; z_2 ~&=~ (-2+3i)\; +\; (3+4i)\\\ nonumber
&=~ 1 + 7i\\\ nonumber
z_1\; -\; z_2 ~&=~ (-2+3i)\; -\; (3+4i)\ nonumber
&=~ -5 - i\\\ nonumber
z_1\, z_2 ~&=~ (-2+3i)\, (3+4i)\\ nonumber
&=~ ((-2) (3) - (3) (4))\; +\; ((-2) (4) + (3) (3)) i\\\ nonumber
&=~ -18 + i\\\ nonumber
\ dfrac {z_1} {z_2} ~&=~\ dfrac {-2+3i} {3+4i}\\\ nonumber
&=~\ dfrac {(-2) (3) + (3) (4)\; +\; ((3) (3) - (-2) (4)) i} {3^2 + 4^2}\\\ nonumber
&=~\ dfrac {6} {25}\; +\;\ dfrac {17} {25}\, i\\\ nonumber
|z_1| ~&=~\ sqrt {(-2) ^2 + 3^2}\\\ nonumber
&=~\ sqrt {13}\\\ nonumber
|z_2| ~&=~\ sqrt {3^2 + 4^2}\\\ nonumber
&=~ 5
\ end {align*}\ nonumber\]
Sabemos que cualquier punto\((x,y) \) en el plano\(xy\) -coordenado que esté a una\(r >0 \) distancia del origen tiene coordenadas\(x=r\,\cos\;\theta \) y\(y=r\,\sin\;\theta \), donde\(\theta \) está el ángulo en posición estándar como en la Figura 6.3.1 (a).
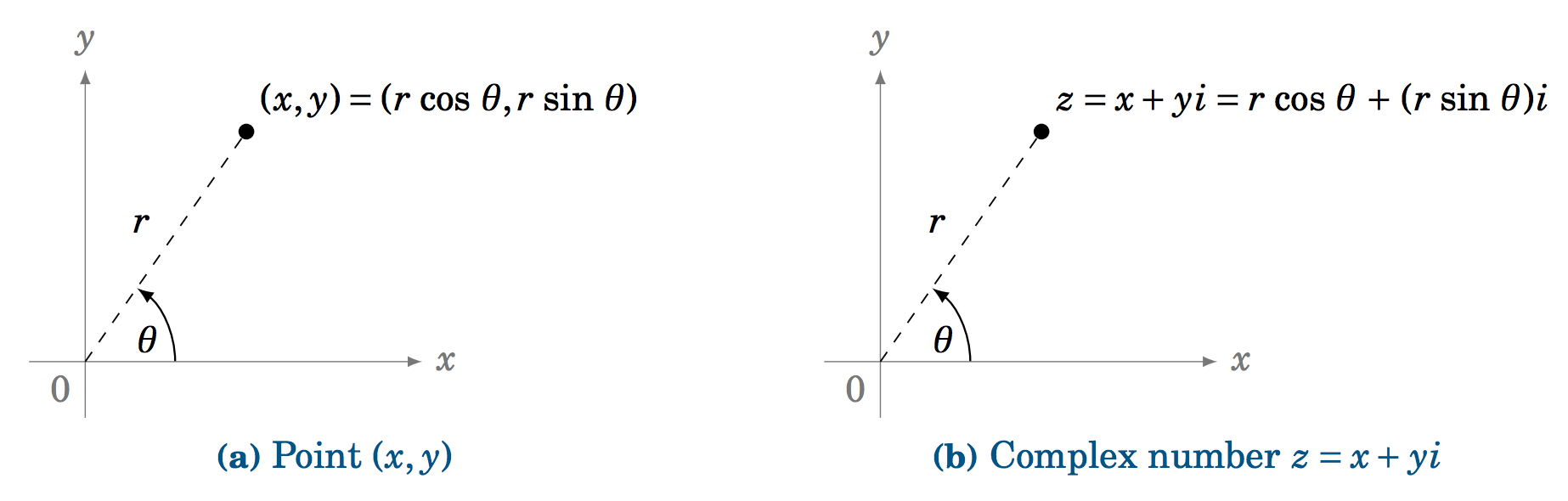
Dejar\(z=x+yi \) ser un número complejo. Podemos representar\(z \) como un punto en el plano complejo, donde el\(x\) eje horizontal representa la parte real de\(z \), y el\(y\) eje vertical representa la parte imaginaria pura de\(z \), como en la Figura 6.3.1 (b). La distancia\(r \) desde\(z \) el origen es, por el Teorema de Pitágoras,\(r = \sqrt{x^2 + y^2} \), que es solo el módulo de\(z \). Y vemos en la Figura 6.3.1 (b) que\(x=r\,\cos\;\theta \) y\(y=r\,\sin\;\theta \), donde\(\theta \) está el ángulo formado por el\(x\) eje positivo y el segmento lineal desde el origen hasta\(z \). Llamamos a este ángulo\(\theta \) el argumento de\(z \). Así, obtenemos la forma trigonométrica (a veces llamada la forma polar) del número complejo\(z\):
Para cualquier número complejo\(z=x+yi \), podemos escribir
\ [\ begin {align}
z ~&=~ r\, (\ cos\;\ theta\; +\; i\,\ sin\;\ theta) ~~, ~\ text {donde}\ label {eqn:polar}\\
r ~&=~ |z| ~=~\ sqrt {x^2 + y^2} ~~\ text {y}\ nonumber\\
\ theta ~&=~\ text {el argumento de\(z\)} ~. \ nonumber\ end {align}\ nonumber\]
La representación a menudo\(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) se abrevía como:
\[ z ~=~ r\,\text{cis}\;\theta\label{eqn:cis} \]
En el caso especial\(z=0 = 0+0i \), el argumento\(\theta \) es indefinido desde entonces\(r=|z|=0 \). Además, tenga en cuenta que el argumento\(\theta \) puede ser sustituido por\(\theta \;+\; 360^\circ k \) o\(\theta \;+\; \pi k \), dependiendo de si está utilizando grados o radianes, respectivamente, para\(k=0 \),\(\pm\,1 \),\(\pm\,2 \),\(... \). Tenga en cuenta también que para\(z=x+yi \) con\(r=|z| \),\(\theta \) debe satisfacer
\[\nonumber \tan\;\theta ~=~ \tfrac{y}{x}~~,~ \cos\;\theta ~=~ \tfrac{x}{r}~~,~ \sin\;\theta ~=~ \tfrac{y}{r}~. \nonumber \]
Representar el número complejo\(-2 - i \) en forma trigonométrica.
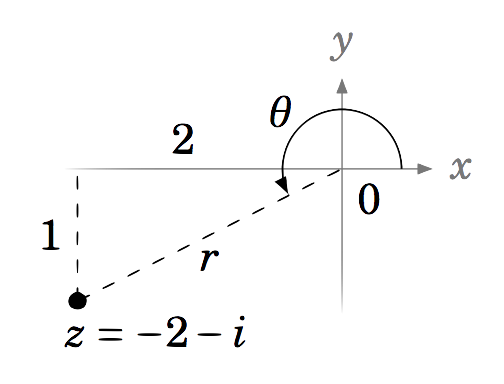
Solución:
Vamos\(z=-2-i=x+yi \), para que\(x=-2 \) y\(y=-1 \). Después\(\theta \) está en QIII, como vemos en la Figura 6.3.2. Entonces ya\(\tan\;\theta = \tfrac{y}{x} = \tfrac{-1}{-2} = \tfrac{1}{2} \), tenemos\(\theta = 206.6^\circ \). También,
\[\nonumber r ~=~ \sqrt{x^2 + y^2} ~=~ \sqrt{(-2)^2 + (-1)^2} ~=~ \sqrt{5} ~. \nonumber \]
Así,\(\boxed{-2 - i = \sqrt{5}\;(\cos\;206.6^\circ \;+\; i\,\sin\;206.6^\circ)}\; \), o\(\sqrt{5}\;\text{cis}\;206.6^\circ \).
Para números complejos en forma trigonométrica, tenemos las siguientes Ecuaciones para multiplicación y división:
Dejar\(z_1 = r_1 \,(\cos\;\theta_1 \;+\; i\,\sin\;\theta_1 ) \) y\(z_2 = r_2 \,(\cos\;\theta_2 \;+\; i\,\sin\;\theta_2 ) \) ser números complejos. Entonces
\ [\ begin {align}
z_1\, z_2 ~&=~ r_1\, r_2\, (\ cos\ ;(\ theta_1 +\ theta_2)\; +\; i\,\ sin\ ;(\ theta_1 +
\ theta_2)) ~\ text {, y}\ label {eqn:complextrigmult}\
\ frac {z_1} {z_2} ~&=~\ frac {r_1} {r_2}\, (\ cos\ ;(\ theta_1 -\ theta_2)\; +\; i\,\ sin\ ;(\ theta_1 -
\ theta_2))\ quad\ texto {si\(z_2 \ne 0 \).} \ label {eqn:complextrigdiv}\ end {align}\]
Las pruebas de estas ecuaciones son sencillas:
\ [\ nonumber\ begin {alinear*}
z_1\, z_2 ~&=~ r_1\, (\ cos\;\ theta_1\; +\; i\,\ sin\;\ theta_1)\;\ cdot\;
r_2\, (\ cos\;\ theta_2\; +\; i\,\ sin\;\ theta_2)\\\ nonúmero
&=~ r_1\, r_2\,\ left [(\ cos\;\ theta_1 ~\ cos\;\ theta_2\; -\;\ sin\;\ theta_1 ~\ sin\;\ theta_2)
\; +\; i\, (\ sin\;\ theta_1 ~\ cos\;\ theta_2\; +\;\ cos\;\ theta_1 ~\ sin\;\ theta_2)\ derecha]\\\ nonumber
&=~ r_1\, r_2\, (\ cos\ ;(\ theta_1 +\ theta_2)\; +\; i\,\ sin\ ;(\ theta_1 +\ theta_2))\ final {alinear*}\ nonumber\]
por la suma Ecuaciones para seno y coseno. Y
\ [\ nonumber\ begin {alinear*}\ frac {z_1} {z_2} ~&=~\ frac {r_1\, (\ cos\;\ theta_1\; +\; i\,\ sin\;\ theta_1)} {
r_2\, (\ cos\;\ theta_2\; +\; i\,\ sin\; theta_2)}\\\ nonúmero
&=~\ frac {r_1} {r_2}\;\ cdot\;\ frac {\ cos\;\ theta_1\; +\; i\,\ sin\;\ theta_1} {
\ cos\;\ theta_2\; +\ ; i\,\ sin\;\ theta_2}\;\ cdot\;\ frac {\ cos\;\ theta_2\; -\; i\,\ sin\;\ theta_2} {
\ cos\;\ theta_2\; -\; i\,\ sin\;\ theta_2}\\\ nonumber
&=~\ frac {_1} {r_2}\;\ cdot\;\ frac {(\ cos\;\ theta_1 ~\ cos\;\ theta_2\; +\;\ sin\;\ theta_1 ~
\ sin\;\ theta_2)\; +\; i\, (\ sin\;\ theta_1 ~ \ cos\;\ theta_2\; -\;\ cos\;\ theta_1 ~
\ sin\;\ theta_2)} {\ cos^2\,\ theta_2\; +\;\ sin^2\,\ theta_2}\\\ nonumber
&=~\ frac {r_1} {r_2}\, (\ cos\ ;(\ theta_1 -\ theta_2)\; +\; i\,\ sin\ ;(\ theta_1 -\ theta_2))
\ end {align*}\ nonumber\]
por la resta Ecuaciones para seno y coseno, y desde\(\cos^2 \,\theta_2 \;+\; \sin^2 \,\theta_2 = 1 \). QED
Observe que las Ecuaciones\ ref {eqn:complextrigmult} y\ ref {eqn:complextrigdiv} dicen que al multiplicar números complejos se multiplican los módulos y se agregan los argumentos, mientras que al dividir números complejos los módulos se dividen y se restan los argumentos. Esto hace que trabajar con números complejos en forma trigonométrica sea bastante simple.
Dejar\(z_1 = 6\,(\cos\;70^\circ \;+\; i\,\sin\;70^\circ ) \) y\(z_1 = 2\,(\cos\;31^\circ \;+\; i\,\sin\;31^\circ ) \). Encontrar\(z_1 \, z_2 \) y\(\frac{z_1}{z_2} \).
Solución
Por Ecuaciones\ ref {eqn:complextrigmult} y\ ref {eqn:complextrigdiv} tenemos
\ [\ nonumber\ begin {alignat*} {3}
z_1\, z_2 ~&=~ (6)\, (2)\, (\ cos\ ;( 70^\ circ + 31^\ circ)\; +\; i\,\ sin\ ;( 70^\ circ +
31^\ circ))\ cuádruple &\ fila derecha\ cuádruple\ caja {z_1\, z_2 ~=~ 12\, (\ cos\; 101^\ circ\; +\;
i\,\ sin\; 101^\ circ)} ~\ texto {, y}\\\ nonúmero
\ frac {z_1} {z_2} ~&=~\ frac {6} {2}\, (\ cos\ ;( 70^\ circ - 31^\ circ)\; +\; i\,\ sin\ ;( 70^\ circ -
31^\ circ))\ quad&&\ Rightarrow\ quad\ boxed {\ frac {z_1} z_2} ~=~ 3\, (\ cos\; 39^\ circ\; +\;
i\,\ sin\; 39^\ circ)} ~.
\ end {alignat*}\ nonumber\]
Para el caso especial cuando\(z_1 = z_2 = z = r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) en Ecuación\ ref {eqn:complextrigmult}, tenemos
\ [\ nonumber\ begin {alinear*}
\ izquierda [r\, (\ cos\;\ theta\; +\; i\,\ sin\;\ theta)\ derecha] ^2 ~&=~
r\ cdot r\, (\ cos\ ;(\ theta +\ theta)\; +\; i\,\ sin\ ;(\ theta +\ theta)\\\ nonumber
&=~ r^2\, (\ cos\; 2\ theta\; +\; i\,\ sin\; 2\ theta) ~,\ end {align*}\ nonumber\]
y así
\ [\ nonumber\ begin {alinear*}\ izquierda [r\, (\ cos\;\ theta\; +\; i\,\ sin\;\ theta)\ derecha] ^3 ~&=~
\ izquierda [r\, (\ cos\;\ theta\; +\; i\,\ sin\;\ theta)\ derecha] ^2\;\ cdot\;
\, (\ cos\;\ theta\; +\; i\,\ sin\;\ theta)\\\ nonúmero
&=~ r^2\, (\ cos\; 2\ theta\; +\; i\,\ sin\; 2\ theta)\;\ cdot\;
r\, (\ cos\;\ theta\; +\; i\,\ sin\;\ theta)\\\ nonúmero
&=~ r^3\, (\ cos\; (2\ theta +\ theta)\; +\; i\,\ sin\ ;( 2\ theta +\ theta))\\ nonumber
&=~ r^3\, (\ cos\; 3\ theta\; +\; i\,\ sin\; 3\ theta) ~,
\ final {alinear*}\ nonumber\]
y continuando así (es decir, por inducción matemática), obtenemos:
Para cualquier entero\(n \ge 1 \),
\ [\ label {eqn:demoivre}
\ izquierda [r\, (\ cos\;\ theta\; +\; i\,\ sin\;\ theta)\ derecha] ^n ~=~
r^n\, (\ cos\; n\ theta\; +\; i\,\ sin\; n\ theta) ~. \ nonumber\]
Definimos\(z^0 = 1 \) y\(z^{-n} = 1/z^n \) para todos los enteros\(n \ge 1 \). Así que por Teorema y Ecuación de De Moivre\ ref {eqn:complextrigmult}, para cualquier\(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) y entero\(n \ge 1 \) obtenemos
\ [\ nonumber\ begin {align*}
z^ {-n} ~&=~\ frac {1} {z^n}\\\ nonumber
&=~\ frac {1\, (\ cos\; 0^\ circ\; +\; i\,\ sin\; 0^\ circ)} {r^n\, (\ cos\; n\ theta\; +\;
i\,\ sin\; n\ theta)}\\\ nonumber
&=~\ frac {1} {r^n}\, (\ cos\ ;( 0^\ circ - n\ theta)\; +\; i\,\ sin\ ;( 0 ^\ circ - n\ theta))\\\ nonumber
&=~ r^ {-n}\, (\ cos\ ;( - n\ theta)\; +\; i\,\ sin\ ;( - n\ theta)) ~,
\ end {align*}\ nonumber\]
y así el Teorema de De Moivre de hecho sostiene para todos los enteros.
Encuentra\((1+i)^{10} \).
Solución
Desde\(1+i = \sqrt{2}\;(\cos\;45^\circ \;+\; i\,\sin\;45^\circ )\) (¿por qué?) , por el Teorema de De Moivre tenemos
\ [\ nonumber (1+i) ^ {10} ~=~ (\ sqrt {2}) ^ {10}\; (\ cos\; 450^\ circ\; +\; i\,\ sin\; 450^\ circ) ~=~
2^ {10/2}\ ;( 0\; +\; i\, (1)) ~=~ 2^5\,\ cpunto\, i ~=~\ en caja {32i} ~. \ nonumber\]
Podemos usar el Teorema de De Moivre para encontrar las\(n^{th} \) raíces de un número complejo. Es decir, dado cualquier número complejo\(z \) y entero positivo\(n \), encontrar todos los números complejos\(w \) tal que\(w^n = z \). Vamos\(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \). Dado que las funciones coseno y seno se repiten cada\(360^\circ \), sabemos que\(z=r\,(\cos\;(\theta + 360^\circ k)\;+\; i\,\sin\;(\theta + 360^\circ k)) \) para\(k=0 \),\(\pm\,1 \),\(\pm\,2 \),\(... \). Ahora vamos a\(w=r_0 \,(\cos\;\theta_0 \;+\; i\,\sin\;\theta_0 ) \) ser una\(n^{th} \) raíz de\(z \). Entonces
\ [\ nonumber\ begin {align*}
w^n ~=~ z\ quad&\ Rightarrow\ quad\ left [r_0\, (\ cos\;\ theta_0\; +\; i\,\ sin\;\ theta_0)\ derecha] ^n
~=~ r\, (\ cos\ ;(\ theta + 360^\ circ k)\; +\; i\,\ sin\ ;(\ theta + 360^\ circ k))\\\ nonúmero
&\ Rightarrow\ quad r_0^n\, (\ cos\; n\ theta_0\; +\; i \,\ sin\; n\ theta_0)
~=~ r\, (\ cos\ ;(\ theta + 360^\ circ k)\; +\; i\,\ sin\ ;(\ theta + 360^\ circ k))\\ nonumber
&\ Rightarrow\ quad r_0^n ~=~ r quad\ text {y}\\ n theta_0 ~=~\ theta + 360^\ circ k\\ nonumber
&\ Rightarrow\ quad r_0 ~=~ r^ {1/n}\ quad\ text {y}\ quad\ theta_0 ~=~
\ frac {\ theta + 360^\ circ k} {n} ~.
\ end {align*}\ nonumber\]
Dado que el coseno y el seno de\(\frac{\theta + 360^\circ k}{n} \) se repetirán para\(k \ge n \), obtenemos la siguiente Ecuación para las\(n^{th} \) raíces de\(z\):
Para cualquier número complejo distinto de cero\(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) y entero positivo\(n \), las\(n^{th}\) raíces\(n \) distintas de\(z \) son
\ [\ label {eqn:nthroots}
r^ {1/n}\,\ izquierda [\ cos\;\ izquierda (\ frac {\ theta + 360^\ circ k} {n}\ derecha)\; +\;
i\,\ sin\;\ izquierda (\ frac {\ theta + 360^\ circ k} {n}\ derecha)\ nonumba]\ er\]
para\(k=0 \),\(1 \),\(2 \),\(... \),\(n-1 \).
Nota: Una\(n^{th} \) raíz de\(z \) suele escribirse como\(z^{1/n} \) o\(\sqrt[n]{z} \). El número\(r^{1/n} \) en la ecuación anterior es la\(n^{th} \) raíz real habitual del número real\(r=|z| \).
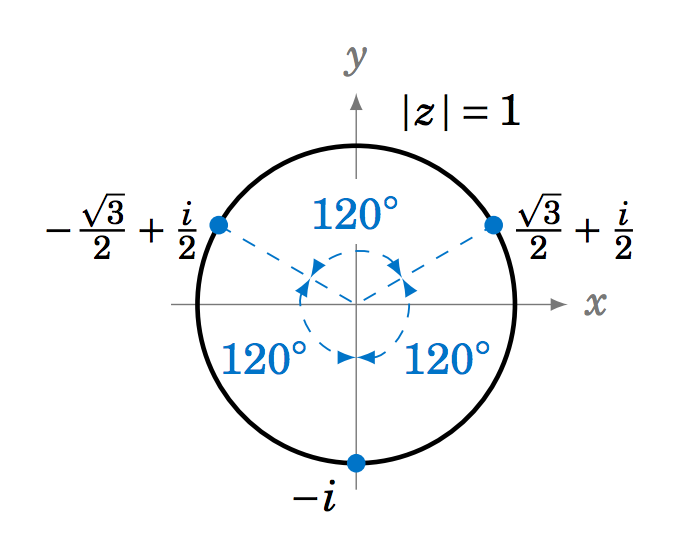
Encuentra las tres raíces cubitas de\(i \).
Solución:
Ya que\(i = 1\,(\cos\;90^\circ \;+\; i\,\sin\;90^\circ) \), las tres raíces cubitas de\(i \) son:
\ [\ nonumber\ begin {alignat*} {3}
\ sqrt [3] {1}\;\ izquierda [\ cos\;\ izquierda (\ frac {90^\ circ + 360^\ circ (0)} {3}\ derecha)\; +\;
i\,\ sin\;\ izquierda (\ frac {90^\ circ + 360^\ circ (0)} {3}\ derecha)\ derecha] ~&=~
\ cos\; 30^\ circ\; +\; i\,\ sin\; 30^\ circ ~&&=~
\ en caja {\ frac {\ sqrt {3}} {2}\; +\;\ frac {1} {2}\, i} ~,\\ nonúmero
\ sqrt [3] {1}\;\ izquierda [\ cos\;\ izquierda (\ frac {90^\ circ + 360^\ circ (1)} {3}\ derecha)\; +\;
i\,\ sin\; izquierda (\ frac {90^\ circ + 360^\ circ (1)} {3}\ derecha)\ derecha] ~&=~
\ cos\; 150^\ circ\; +\; i\,\ sin\; 150^\ circ ~&&=~
\ en caja {-\ frac {\ sqrt {3}} {2}\; +\;\ frac {1} {2}\, i} ~,\\ nonumber
\ sqrt [3] {1}\;\ izquierda [\ cos\;\ izquierda (\ frac {90^\ circ + 360^\ circ (2)} {3}\ derecha)\; +\;
i\,\ sin\;\ izquierda (\ frac {90^\ circ + 360^\ circ (2)} {3}\ derecha)\ derecha] ~&=~
\ cos\; 270^\ circ\; +\; i\,\ sin\; 270^\ circ ~& amp; &=~\ en caja {-i}
\ end {alignat*}\ nonumber\]
Observe en el Ejemplo 6.13 que las tres raíces cubitas de\(i \) son puntos igualmente espaciados a lo largo del círculo unitario\(|z|=1 \) en el plano complejo, como se muestra en la Figura 6.3.3. Vemos que las raíces cubicales consecutivas están\(120^\circ \) separadas. En general, las\(n \)\(n^{th} \) raíces de un número complejo\(z \) serán puntos igualmente espaciados a lo largo del círculo de radio\(|z|^{1/n} \) en el plano complejo, con raíces consecutivas separadas por\(\tfrac{360^\circ}{n} \).
En matemáticas superiores el Teorema Fundamental del Álgebra afirma que cada polinomio de grado\(n \) con coeficientes complejos tiene raíces\(n \) complejas (algunas de las cuales pueden repetirse). En particular, cada número real\(a \) tiene\(n \)\(n^{th} \) raíces (siendo las raíces de\(z^n - a\)). Por ejemplo, las raíces cuadradas de\(1 \) son\(\pm\,1 \), y las raíces cuadradas de\(-1 \) son\(\pm\,i \).


