6.4: Coordenadas polares

Supongamos que desde el punto\((1,0) \) en el plano\(xy\) -coordenada dibujamos una espiral alrededor del origen, de tal manera que la distancia entre dos puntos cualesquiera separados por\(360^\circ \) a lo largo de la espiral es siempre\(1 \), como en la Figura 6.4.1. No podemos expresar esta espiral como\(y=f(x) \) para alguna función\(f \) en coordenadas cartesianas, ya que su gráfica viola la regla vertical.

Figura 6.4.1

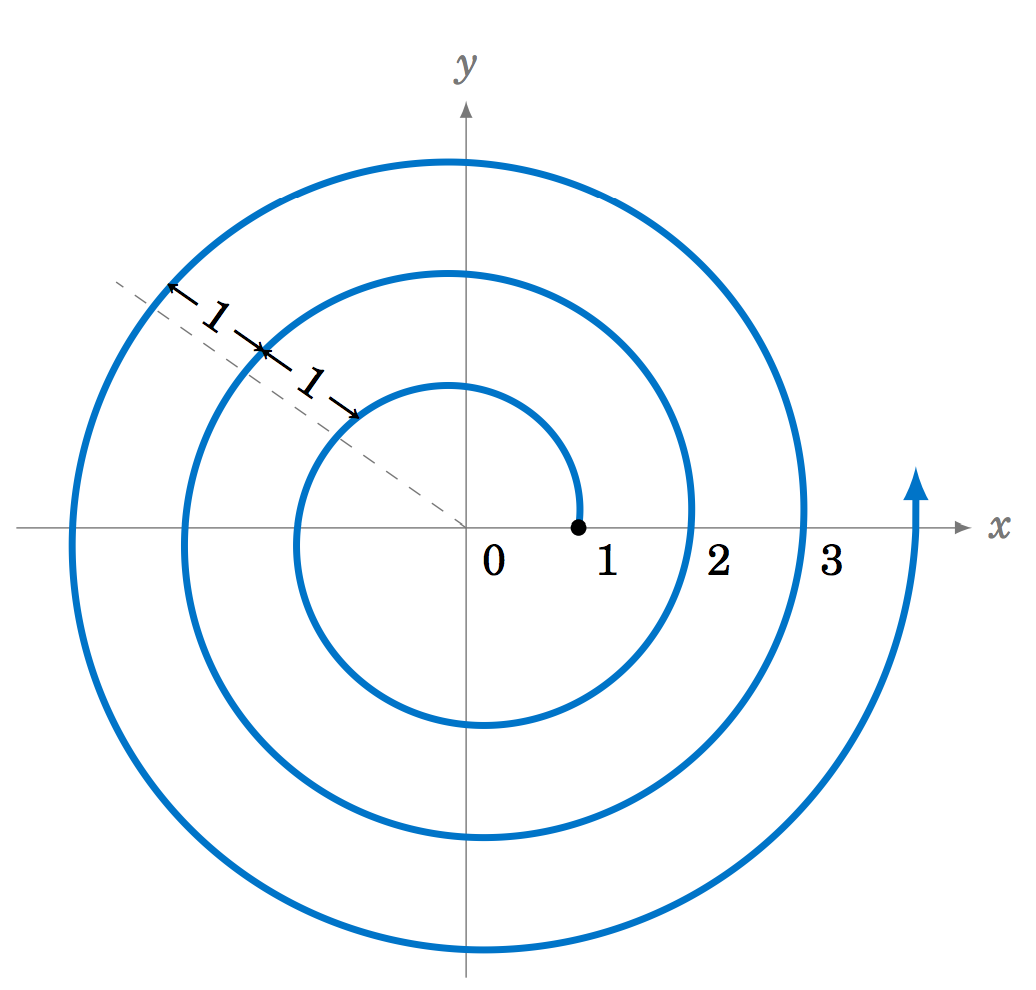
Sin embargo, esta espiral sería simple de describir utilizando el sistema de coordenadas polares. Recordemos que cualquier punto\(P \) distinto del origen (denotado por\(O\)) en el plano\(xy\) -coordenada es una\(r>0 \) distancia del origen, y el rayo\(\overrightarrow{OP} \) forma un ángulo\(\theta \) con el\(x\) eje positivo, como en la Figura 6.4.2. Llamamos al par\((r,\theta) \) las coordenadas polares de\(P \), y el\(x\) eje positivo se llama el eje polar de este sistema de coordenadas. Tenga en cuenta que\((r,\theta) = (r,\theta + 360^\circ k) \) para\(k=0 \)\(\pm\,1 \),\(\pm\,2 \),\(... \), entonces (a diferencia de las coordenadas cartesianas) las coordenadas polares de un punto no son únicas.

Figura 6.4.2 Coordenadas polares\((r,θ)\) y Figura 6.4.3 Negativas\(r:\, (−r,θ)\)

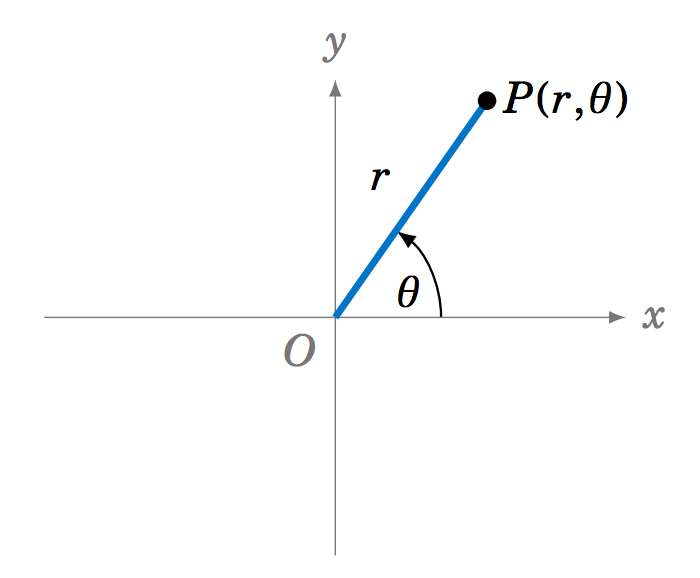
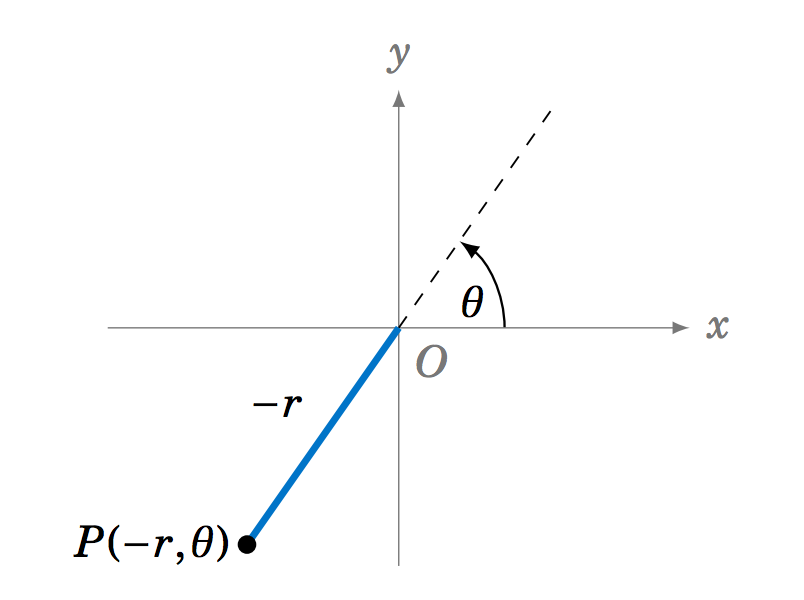
En coordenadas polares adoptamos la convención que\(r \) puede ser negativa, definiendo\((-r,\theta) = (r,\theta + 180^\circ) \) para cualquier ángulo\(\theta \). Es decir, el rayo\(\overrightarrow{OP} \) se dibuja en dirección opuesta al ángulo\(\theta \), como en la Figura 6.4.3. Cuando\(r=0 \), el punto\((r,\theta) = (0,\theta) \) es el origen\(O \), independientemente del valor de\(\theta \).

Puede estar familiarizado con el papel gráfico, para trazar puntos o funciones dadas en coordenadas cartesianas (a veces también llamadas coordenadas rectangulares). Dicho papel consiste en una rejilla rectangular. Un papel gráfico similar existe para trazar puntos y funciones en coordenadas polares, similar a la Figura 6.4.4.

Figura 6.4.4 Gráfico de coordenadas polares

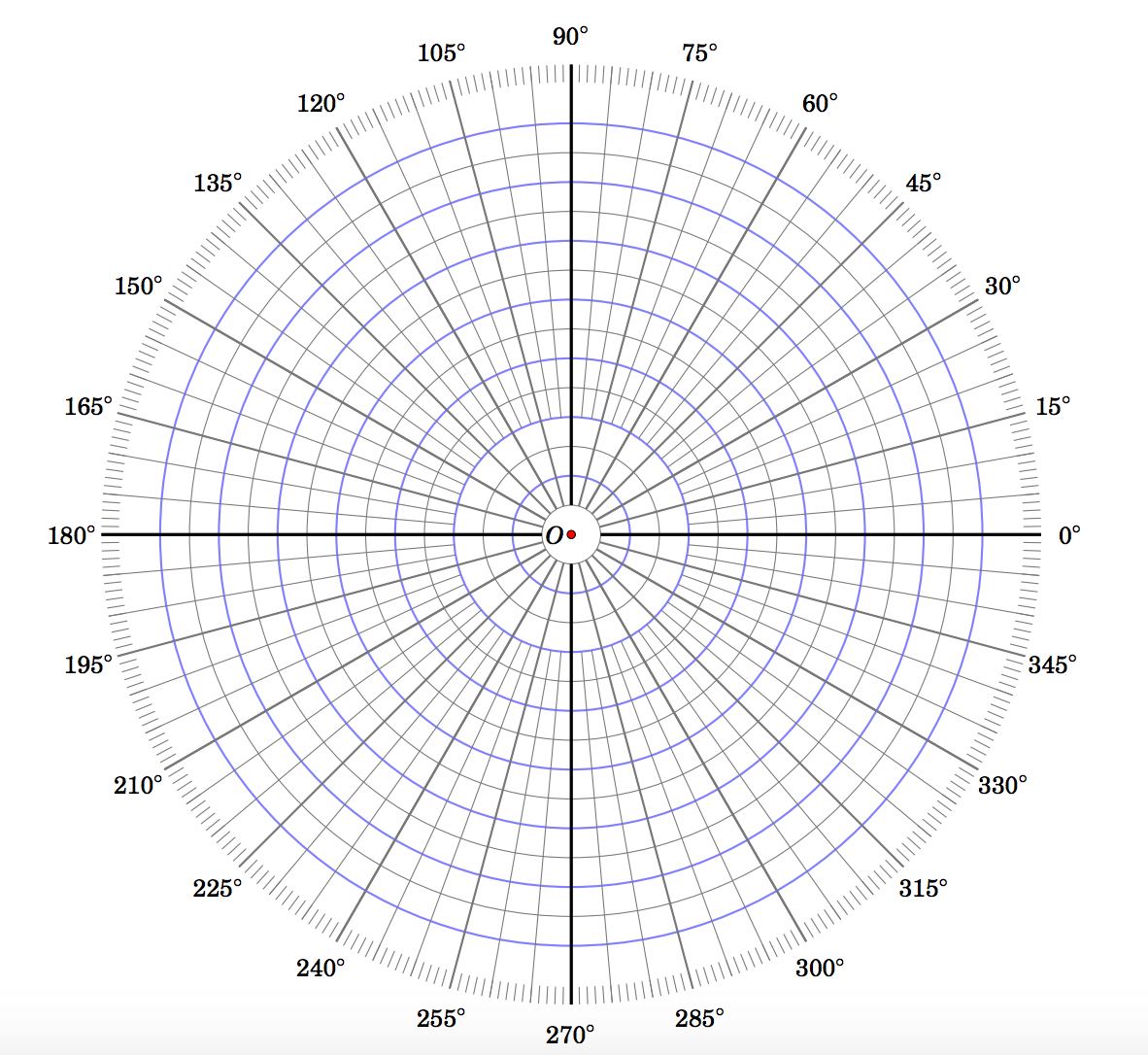
El ángulo se\(\theta \) puede dar en grados o radianes, lo que sea más conveniente. Los radianes son a menudo preferidos al graficar funciones en coordenadas polares. La razón es que, a diferencia de los grados, los radianes pueden considerarse “sin unidades” (como mencionamos en el Capítulo 4). Esto es deseable cuando una función dada en coordenadas polares se expresa\(r \) como una función de\(\theta \) (similar a cómo, en coordenadas cartesianas\((x,y) \), las funciones suelen expresarse\(y \) como una función de\(x\)). Por ejemplo, si una
función en coordenadas polares se escribe como\(r = 2\,\theta \), entonces\(r \) tendría las mismas unidades que\(\theta \). Pero\(r \) debería ser una cantidad sin unidades, de ahí que usar radianes para tenga más\(\theta \) sentido en este caso.

Ejemplo 6.14

Exprese la espiral de la Figura 6.4.1 en coordenadas polares.

Solución

Utilizaremos radianes para\(\theta \). El objetivo es encontrar alguna ecuación que involucre\(r \) y\(\theta \) que describa la espiral. Vemos que

\ [\ nonumber\ begin {align*}
\ theta ~=~ 0\ quad&\ Rightarrow\ quad r ~=~ 1\\ [4pt]
\ theta ~=~ 2\ pi\ quad&\ Rightarrow\ quad r ~=~ 2\\ [4pt]
\ theta ~=~ 4\ pi\ quad&\ Rightarrow quad\ r ~=~ 3\ [4pt]
&\ vdots\\ [4pt]
\ theta ~=~ 2\ pi\, k\ quad&\ Rightarrow\ quad r ~=~ 1+k\\ [4pt]
\ end {align*}\ nonumber\]

para\(k=0,1,2,\ldots \). De hecho, esa última relación se mantiene para cualquier número real no negativo\(k \) (¿por qué?). Así que para cualquier\(\theta \ge 0 \),

\ [\ theta ~=~ 2\ pi\, k\ quad\ Rightarrow\ quad k ~=~\ frac {\ theta} {2\ pi}\ quad\ Rightarrow\ quad r ~=~
1 + k ~=~ 1 +\ frac {\ theta} {2\ pi} ~. \ nonumber\]

De ahí que la espiral se pueda escribir como\(\fbox{\(r ~=~ 1 + \frac{\theta}{2\pi}\)}\) para\(\theta \ge 0 \). La gráfica se muestra en la Figura 6.4.5, junto con los comandos de Gnuplot para crear la gráfica.

Figura 6.4.5\(r=1+\frac{\theta}{2\pi}\)

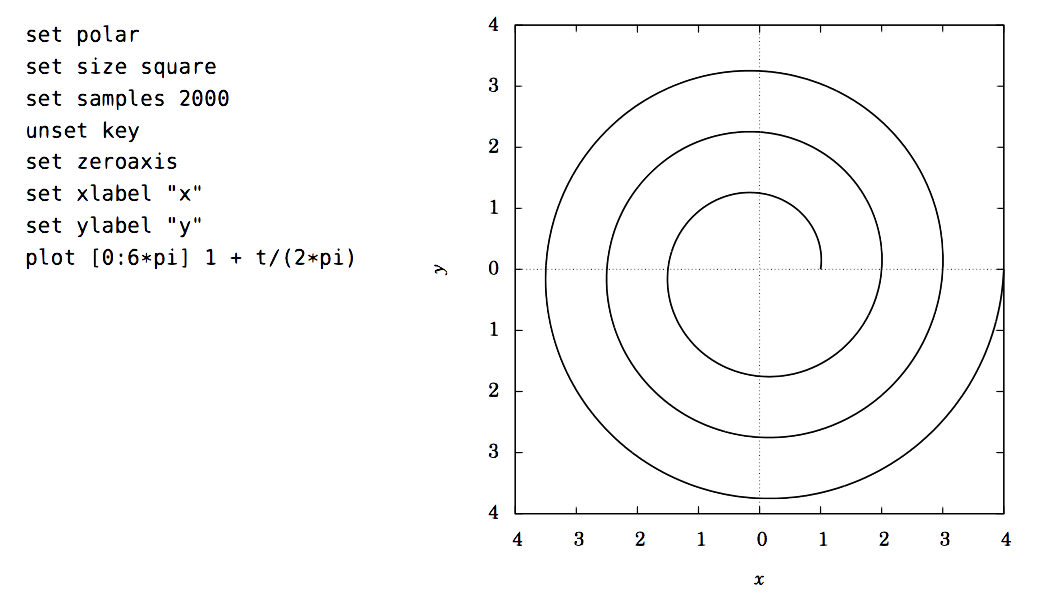
Tenga en cuenta que al usar el\(\texttt{set polar}\) comando, Gnuplot asumirá que la función que se está trazando es\(r \) como una función de\(\theta \) (representada por la variable\(\texttt{t}\) en Gnuplot).

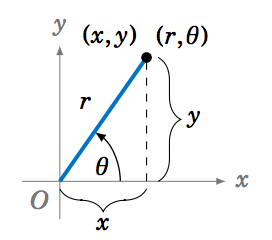
La Figura 6.4.6 muestra cómo convertir entre coordenadas polares y coordenadas cartesianas. Para un punto con coordenadas polares\((r,\theta) \) y coordenadas cartesianas\((x,y)\):

Figura 6.4.6

Polar a Cartesiano:

\[\label{eqn:polartorect} \boxed{ x ~=~ r\,\cos\;\theta \qquad y ~=~ r\,\sin\;\theta } \]

Cartesiano a Polar:

\[\label{eqn:recttopolar} \boxed{ r ~=~ \pm\;\sqrt{x^2 ~+~ y^2} \qquad \tan\;\theta ~=~ \frac{y}{x} ~~\text{if \(x \ne 0\)} } \]

Tenga en cuenta que en la Ecuación\ ref {eqn:recttopolar}, si\(x = 0 \) entonces\(\theta = \pi/2 \) o\(\theta = 3\pi/2 \). También, si\(x \ne 0 \) y\(y \ne 0 \) entonces las dos posibles soluciones para\(\theta \) en la ecuación\(\tan\;\theta ~=~ \frac{y}{x} \) están en cuadrantes opuestos (for\(0 \le \theta < 2\pi\)). Si el ángulo\(\theta \) está en el mismo cuadrante que el punto\((x,y) \), entonces\(r = \sqrt{x^2 ~+~ y^2} \) (es decir,\(r \) es positivo); de lo contrario\(r = -\sqrt{x^2 ~+~ y^2} \) (es decir,\(r \) es negativo).

Ejemplo 6.15

Convierte los siguientes puntos de coordenadas polares a coordenadas cartesianas:

1. \((2,30^\circ)\)
2. \((3,3\pi/4)\)
3. \((-1,5\pi/3)\)

Solución

(a) Usando la ecuación\ ref {eqn:polartorect} con\(r=2 \) y\(\theta = 30^\circ \), obtenemos:

\ [(x, y) ~=~ (r\,\ cos\;\ theta, r\,\ sin\;\ theta) ~=~ (2\,\ cos\; 30^\ circ,2\,\ sin\; 30^\ circ) ~=~
\ izquierda (2\;\ cdot\;\ tfrac {\ sqrt {3}} {2}, 2\;\ cdot\;\ tfrac {1} {2}\ derecha)\ quad\ fila derecha\ cuádruple
\ en caja {(x, y) ~=~\ izquierda (\ sqrt {3} ,1\ derecha)}
\ nonumber\]

(b) Usando la ecuación\ ref {eqn:polartorect} con\(r=3 \) y\(\theta = 3\pi/4 \), obtenemos:

\ [(x, y) ~=~ (r\,\ cos\;\ theta, r\,\ sin\;\ theta) ~=~\ left (3\,\ cos\;\ tfrac {3\ pi} {4} ,3\,\ sin\;\ tfrac {3\ pi} {4}
\ derecha) ~=~\ izquierda (3\;\ cdot\;\ tfrac {-1} {\ sqrt {2}}, 3\;\ cdot\;\ tfrac {1} {\ sqrt {2}}\ derecha)
\ quad\ Rightarrow\ quad\ boxed {(x, y) ~=~\ left (\ tfrac {-3} {\ sqrt {2}},\ tfrac {3} {\ sqrt {2}}\ derecha)}
\ nonumber\]

(c) Usando la ecuación\ ref {eqn:polartorect} con\(r=-1 \) y\(\theta = 5\pi/3 \), obtenemos:

\ [(x, y) ~=~ (r\,\ cos\;\ theta, r\,\ sin\;\ theta) ~=~\ izquierda (-1\,\ cos\;\ tfrac {5\ pi} {3}, -1\,\ sin\;\ tfrac {5\ pi} {3}
\ derecha) ~=~\ izquierda (-1\;\ cdot\;\ tfrac {1} {2}, -1\;\ cdot\;\ tfrac {-\ sqrt {3}} {2}\ derecha)
\ quad\ Rightarrow\ quad\ boxed {(x, y) ~=~\ izquierda (-\ tfrac {1} {2},\ tfrac {\ sqrt {3}} {2}\ derecha )}
\ nonumber\]

Ejemplo 6.16

Convierte los siguientes puntos de coordenadas cartesianas a coordenadas polares:

1. \((3,4)\);
2. \((-5,-5)\)

Solución

(a) Usando fórmula\ ref {eqn:recttopolar} con\(x=3 \) y\(y=4 \), obtenemos:

\ [\ tan\;\ theta ~=~\ frac {y} {x} ~=~\ frac {4} {3}\ cuádruple\ fila derecha\ quad\ theta ~=~ 53.13^\ circ\ quad
\ texto {o}\ quad\ theta ~=~ 233.13^\ circ\ nonumber\]

Ya que\(\theta = 53.13^\circ \) está en el mismo cuadrante (QI) que el punto\((x,y) = (3,4) \), podemos tomar
\(r ~=~ \sqrt{x^2 + y^2} = \sqrt{3^2 + 4^2} = 5 \). Por lo tanto,\(\boxed{(r,\theta) = (5,53.13^\circ)}\).

Tenga en cuenta que si hubiéramos usado\(\theta = 233.13^\circ \), entonces lo habríamos hecho\((r,\theta) =(-5,233.13^\circ) \).

(b) Usando la ecuación\ ref {eqn:recttopolar} con\(x=-5 \) y\(y=-5 \), obtenemos:

\ [\ tan\;\ theta ~=~\ frac {y} {x} ~=~\ frac {-5} {-5} ~=~ 1\ quad\ Rightarrow\ quad\ theta ~=~ 45^\ circ\ quad
\ text {o}\ quad\ theta ~=~ 225^\ circ\ nonumber\]

Ya que\(\theta = 225^\circ \) está en el mismo cuadrante (QIII) que el punto\((x,y) = (-5,-5) \), podemos tomar
\(r ~=~ \sqrt{x^2 + y^2} = \sqrt{(-5)^2 + (-5)^2} = 5\,\sqrt{2} \). Por lo tanto,\(\boxed{(r,\theta) =(5\,\sqrt{2},225^\circ)}\).

Tenga en cuenta que si hubiéramos usado\(\theta = 45^\circ \), entonces lo habríamos hecho\((r,\theta) = (-5\,\sqrt{2},45^\circ) \).

Ejemplo 6.17

Escribe la ecuación\(x^2 + y^2 = 9 \) en coordenadas polares.

Solución

Esta es solo la ecuación de un círculo de radio\(3 \) centrado en el origen. Ya que\(r = \pm\sqrt{x^2 + y^2} = \pm\sqrt{9} \), en coordenadas polares la ecuación se puede escribir de manera simple\(\boxed{r = 3}\).

Ejemplo 6.18

Escribe la ecuación\(x^2 + (y-4)^2 = 16 \) en coordenadas polares.

Solución

Esta es la ecuación de un círculo de radio\(4 \) centrado en el punto\((0,4) \). Ampliando la ecuación, obtenemos:

\ [\ begin {align*}
x^2 ~+~ (y-4) ^2 ~&=~ 16\\ [4pt]
x^2 ~+~ y^2 ~-~ 8y ~+~ 16 ~&=~ 16\\ [4pt]
x^2 ~+~ y^2 ~&=~ 8y\\ [4pt]
r^2 ~&=~ 8\, r sin\\;\ theta\\ [4pt]
r ~&=~ 8\,\ sin\;\ theta
\ final {alinear*}\ nonumber\]

¿Por qué podríamos cancelar\(r \) de ambos lados en el último paso? Debido a que el punto\((0,0)\) está en el círculo, cancelar\(r \) no elimina\(r=0 \) como solución potencial de la ecuación (ya que\(\theta = 0^\circ \) haría\(r = 8\,\sin\;\theta = 8\,\sin\;0^\circ = 0\)). Así, la ecuación es\(\boxed{r = 8\,\sin\;\theta}\).

Ejemplo 6.19

Escribe la ecuación\(y = x \) en coordenadas polares.

Solución

Esta es la ecuación de una línea a través del origen. Entonces cuando\(x=0 \), eso lo sabemos\(y=0 \). Cuando\(x \ne 0 \), obtenemos:

\ [\ begin {align*}
y ~&=~ x\\ [4pt]
\ frac {y} {x} ~&=~ 1\\ [4pt]
\ tan\;\ theta ~&=~ 1\\ [4pt]
\ theta ~&=~ 45^\ circ
\ end {align*}\ nonumber\]

Ya que no hay restricción sobre\(r \), podríamos tener\(r=0 \) y\(\theta = 45^\circ \), que se encargaría del caso\(x = 0 \) (desde entonces\((x,y) = (0,0) \), que es lo mismo que\((r,\theta) = (0,45^\circ)) \). Así, la ecuación es\(\boxed{\theta = 45^\circ}\).

Ejemplo 6.20

Demostrar que la distancia\(d \) entre dos puntos\((r_1 , \theta_1) \) y\((r_2 , \theta_2) \) en coordenadas polares es

\[ d ~=~ \sqrt{r_1^2 ~+~ r_2^2 ~-~ 2r_1r_2\,\cos\;(\theta_1 - \theta_2)} ~~.\nonumber \]

Solución

La idea aquí es usar la fórmula de distancia en coordenadas cartesianas, luego convertirla en coordenadas polares. Así que escribe

\ [\ nonumber\ begin {alignat*} {4}
x_1 ~&=~ r_1\,\ cos\;\ theta_1\ qquad& y_1 ~&=~ r_1\,\ sin\;\ theta_1\ [4pt]
x_2 ~&=~ r_2\,\ cos\;\ theta_2\ qquad& ~&=~ =~ r_2\,\ sin\;\ theta_2 ~.
\ end {alignat*}\ nonumber\]

Entonces\((x_1,y_1) \) y\((x_2,y_2) \) son los equivalentes cartesianos de\((r_1 , \theta_1) \) y\((r_2 , \theta_2) \), respectivamente. Así, mediante la fórmula de distancia de coordenadas cartesianas,

\ [\ begin {align*}
d^2 ~&=~ (x_1 - x_2) ^2 ~+~ (y_1 - y_2) ^2\\ [4pt]
&=~ (r_1\,\ cos\;\ theta_1 - r_2\,\ cos\;\ theta_2) ^2 ~+~ (r_1\,\ sin\;\ theta_2) ^2 ~+~ (r_1\,\ sin\;\ theta_a_1 - r_2\,\ sin\;\ theta_2) ^2\\ [4pt]
&=~ r_1^2\ cos^2\;\ theta_1 ~-~ 2r_1 r_2\ cos\;\ theta_1~\ cos\;\ theta_2 ~+~ r_2^2\ cos^2\;\ theta_2 ~+~
r_1^2\ sin^2\;\ theta_1 ~-~ 2r_1 r_2\ sin\;\ theta_1~\ sin\;\ theta_2 ~+~ r_2^2\ sin^2\;\ theta_2\;\ theta_2\ [4pt]
&=~ r_1^2 (\ 2\;\ theta_1 ~+~\ sin^2\;\ theta_1) ~+~ r_2^2 (\ cos^2\;\ theta_2 ~+~\ sin^2\;\ theta_2) ~-~
2r_1 r_2 (\ cos\;\ theta_1~\ cos\;\ theta_2 ~ +~\ sin\;\ theta_1~\ sin\;\ theta_2)\\ [4pt]
d^2 ~&=~ r_1^2 ~+~ r_2^2 ~-~ 2r_1r_2\,\ cos\ ;(\ theta_1 -\ theta_2) ~,
\ end {align*}\ noner\ umber

por lo que el resultado sigue tomando raíces cuadradas de ambos lados.

En el Ejemplo 6.17 vimos que la ecuación\(x^2 + y^2 = 9 \) en coordenadas cartesianas podría expresarse como\(r = 3 \) en coordenadas polares. Esta ecuación describe un círculo centrado en el origen, por lo que el círculo es simétrico con respecto al origen. En general, las coordenadas polares son útiles en situaciones en las que hay simetría sobre el origen (aunque hay otras situaciones), que surgen en muchas aplicaciones físicas.