4.1: Funciones exponenciales
- Page ID
- 121434
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Evaluar funciones exponenciales.
- Encuentra la ecuación de una función exponencial.
- Utilizar fórmulas de interés compuesto.
- Evaluar funciones exponenciales con base\(e\).
India es el segundo país más poblado del mundo con una población de alrededor de\(1.25\) mil millones de personas en 2013. La población crece a un ritmo de aproximadamente\(.2\%\) cada año. Si esta tasa continúa, la población de la India superará a la población china para el año 2031. Cuando las poblaciones crecen rápidamente, a menudo decimos que el crecimiento es “exponencial”, lo que significa que algo está creciendo muy rápidamente. Para un matemático, sin embargo, el término crecimiento exponencial tiene un significado muy específico. En esta sección, echaremos un vistazo a las funciones exponenciales, que modelan este tipo de rápido crecimiento.
Al explorar el crecimiento lineal, observamos una tasa constante de cambio, un número constante por el cual la salida aumentó por cada unidad de aumento en la entrada. Por ejemplo, en la ecuación\(f(x)=3x+4\), la pendiente nos dice que la salida aumenta\(3\) cada vez que la entrada aumenta en\(1\). El escenario en el ejemplo poblacional de la India es diferente porque tenemos un cambio porcentual por unidad de tiempo (en lugar de un cambio constante) en el número de personas.
Definición de una función exponencial
Un estudio encontró que el porcentaje de la población vegana en Estados Unidos se duplicó de 2009 a 2011. En 2011,\(2.5\%\) de la población era vegana, adhiriéndose a una dieta que no incluye ningún producto animal, ni carne, aves, pescado, lácteos ni huevos. Si esta tasa continúa, los veganos conformarán a\(10\%\) la población estadounidense en 2015,\(40\%\) en 2019 y\(80\%\) en 2050.
¿Qué significa exactamente crecer exponencialmente? ¿Qué tiene en común la palabra doble con incremento porcentual? La gente arroja estas palabras erradamente. ¿Estas palabras se usan correctamente? Las palabras ciertamente aparecen frecuentemente en los medios de comunicación.
- El cambio porcentual se refiere a un cambio basado en un porcentaje de la cantidad original.
- El crecimiento exponencial se refiere a un incremento basado en una tasa de cambio multiplicativa constante sobre incrementos iguales de tiempo, es decir, un incremento porcentual de la cantidad original a lo largo del tiempo.
- Decaimiento exponencial se refiere a una disminución basada en una tasa de cambio multiplicativa constante sobre incrementos iguales de tiempo, es decir, una disminución porcentual de la cantidad original a lo largo del tiempo.
Para que obtengamos una comprensión clara del crecimiento exponencial, contrastemos el crecimiento exponencial con el crecimiento lineal. Construiremos dos funciones. La primera función es exponencial. Comenzaremos con una entrada de\(0\), y aumentaremos cada entrada por\(1\). Duplicaremos las salidas consecutivas correspondientes. La segunda función es lineal. Comenzaremos con una entrada de\(0\), y aumentaremos cada entrada por\(1\). Sumaremos\(2\) a las salidas consecutivas correspondientes (Tabla\(\PageIndex{1}\)).
De Table\(\PageIndex{1}\) podemos inferir que para estas dos funciones, el crecimiento exponencial empequeñece el crecimiento lineal.
- El crecimiento exponencial se refiere al valor original del rango aumenta en el mismo porcentaje sobre incrementos iguales encontrados en el dominio.
- Crecimiento lineal se refiere al valor original del rango aumenta en la misma cantidad sobre incrementos iguales encontrados en el dominio.
| \(x\) | \(f(x)=2^x\) | \(g(x)=2x\) |
|---|---|---|
| \ (x\)” style="vertical-align:middle; ">0 | \ (f (x) =2^x\)” style="vertical-align:middle; ">1 | \ (g (x) =2x\)” style="vertical-align:middle; ">0 |
| \ (x\)” style="vertical-align:middle; ">1 | \ (f (x) =2^x\)” style="vertical-align:middle; ">2 | \ (g (x) =2x\)” style="vertical-align:middle; ">2 |
| \ (x\)” style="vertical-align:middle; ">2 | \ (f (x) =2^x\)” style="vertical-align:middle; ">4 | \ (g (x) =2x\)” style="vertical-align:middle; ">4 |
| \ (x\)” style="vertical-align:middle; ">3 | \ (f (x) =2^x\)” style="vertical-align:middle; ">8 | \ (g (x) =2x\)” style="vertical-align:middle; ">6 |
| \ (x\)” style="vertical-align:middle; ">4 | \ (f (x) =2^x\)” style="vertical-align:middle; ">16 | \ (g (x) =2x\)” style="vertical-align:middle; ">8 |
| \ (x\)” style="vertical-align:middle; ">5 | \ (f (x) =2^x\)” style="vertical-align:middle; ">32 | \ (g (x) =2x\)” style="vertical-align:middle; ">10 |
| \ (x\)” style="vertical-align:middle; ">6 | \ (f (x) =2^x\)” style="vertical-align:middle; ">64 | \ (g (x) =2x\)” style="vertical-align:middle; ">12 |
Al parecer, la diferencia entre “el mismo porcentaje” y “la misma cantidad” es bastante significativa. Para el crecimiento exponencial, sobre incrementos iguales, la tasa de cambio multiplicativa constante resultó en duplicar la salida cada vez que la entrada aumentaba en uno. Para el crecimiento lineal, la tasa aditiva constante de cambio sobre incrementos iguales resultó en sumar\(2\) a la salida cada vez que la entrada se incrementó en uno.
La forma general de la función exponencial es\(f(x)=ab^x\), donde\(a\) está cualquier número distinto de cero,\(b\) es un número real positivo no igual a\(1\).
- Si\(b>1\), la función crece a una velocidad proporcional a su tamaño.
- Si\(0<b<1\), la función decae a una tasa proporcional a su tamaño.
Veamos la función\(f(x)=2^x\) de nuestro ejemplo. Crearemos una tabla (Tabla\(\PageIndex{2}\)) para determinar las salidas correspondientes a lo largo de un intervalo en el dominio de\(−3\) a\(3\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(2^{−3}=\dfrac{1}{8}\) | \(2^{−2}=\dfrac{1}{4}\) | \(2^{−1}=\dfrac{1}{2}\) | \(2^0=1\) | \(2^1=2\) | \(2^2=4\) | \(2^3=8\) |
Examinemos la gráfica de\(f\) trazando los pares ordenados de Tabla\(\PageIndex{2}\) y luego hagamos algunas observaciones\(\PageIndex{1}\).
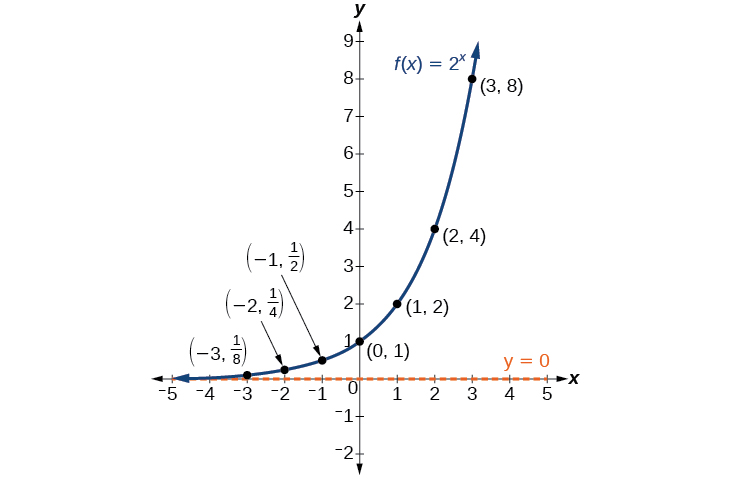
Definamos el comportamiento de la gráfica de la función exponencial\(f(x)=2^x\) y resaltemos algunas de sus características clave.
- el dominio es\((−\infty,\infty)\),
- el rango es\((0,\infty)\),
- como\(x\rightarrow \infty\)\(f(x)\rightarrow \infty\),
- como\(x\rightarrow −\infty\)\(f(x)\rightarrow 0\),
- \(f(x)\)siempre va en aumento,
- la gráfica de nunca\(f(x)\) tocará el eje x porque la base dos elevada a cualquier exponente nunca tiene el resultado de cero.
- \(y=0\)es la asíntota horizontal.
- la intercepción y es\(1\).
Para cualquier número real\(x\), una función exponencial es una función con la forma
\[f(x)=ab^x\]
donde
- \(a\)es un número real distinto de cero llamado valor inicial y
- \(b\)es cualquier número real positivo tal que\(b≠1\).
- El dominio de\(f\) es todo números reales.
- El rango de\(f\) es todos los números reales positivos si\(a>0\).
- El rango de\(f\) es todos los números reales negativos si\(a<0\).
- La y -intercepción es\((0,a)\), y la asíntota horizontal es\(y=0\).
¿Cuáles de las siguientes ecuaciones no son funciones exponenciales?
- \(f(x)=4^{3(x−2)}\)
- \(g(x)=x^3\)
- \(h(x)=\left(\dfrac{1}{3}\right)^x\)
- \(j(x)=(−2)^x\)
Solución
Por definición, una función exponencial tiene una constante como base y una variable independiente como exponente. Así,\(g(x)=x^3\) no representa una función exponencial porque la base es una variable independiente. De hecho,\(g(x)=x^3\) es una función de potencia.
Recordemos que la base\(b\) de una función exponencial es siempre una constante positiva, y\(b≠1\). Así,\(j(x)={(−2)}^x\) no representa una función exponencial porque la base,\(−2\), es menor que\(0\).
¿Cuál de las siguientes ecuaciones representa funciones exponenciales?
- \(f(x)=2x^2−3x+1\)
- \(g(x)={0.875}^x\)
- \(h(x)=1.75x+2\)
- \(j(x)={1095.6}^{−2x}\)
- Contestar
-
\(g(x)={0.875}^x\)y\(j(x)={1095.6}^{−2x}\) representan funciones exponenciales.
Evaluación de funciones exponenciales
Recordemos que la base de una función exponencial debe ser un número real positivo distinto a\(1\). ¿Por qué limitamos la base bb a valores positivos? Para asegurar que las salidas sean números reales. Observe lo que sucede si la base no es positiva:
- Dejar\(b=−9\) y\(x=\dfrac{1}{2}\). Entonces\(f(x)=f\left(\dfrac{1}{2}\right)={(−9)}^{\dfrac{1}{2}}=\sqrt{−9}\), que no es un número real.
¿Por qué limitamos la base a valores positivos distintos a\(1\)? Porque base\(1\) da como resultado la función constante. Observe lo que sucede si la base es\(1\):
- Vamos\(b=1\). Entonces\(f(x)=1^x=1\) por cualquier valor de\(x\).
Para evaluar una función exponencial con la forma\(f(x)=b^x\), simplemente\(x\) sustituimos por el valor dado, y calculamos la potencia resultante. Por ejemplo:
Vamos\(f(x)=2^x\). ¿Qué es\(f(3)\)?
\[\begin{align*} f(x)&= 2^x\\ f(3)&= 2^3 \qquad \text{Substitute } x=3\\ &= 8 \qquad \text{Evaluate the power} \end{align*}\]
Para evaluar una función exponencial con una forma distinta a la forma básica, es importante seguir el orden de las operaciones. Por ejemplo:
Vamos\(f(x)=30{(2)}^x\). ¿Qué es\(f(3)\)?
\[\begin{align*} f(x)&= 30{(2)}^x\\ f(3)&= 30{(2)}^3 \qquad \text{Substitute } x=3\\ &= 30(8) \qquad \text{Simplify the power first}\\ &= 240 \qquad \text{Multiply} \end{align*}\]
Tenga en cuenta que si no se siguiera el orden de las operaciones, el resultado sería incorrecto:
\[f(3)=30{(2)}^3≠{60}^3=216,000 \nonumber\]
Vamos\(f(x)=5{(3)}^{x+1}\). Evaluar\(f(2)\) sin usar una calculadora.
Solución
Seguir el orden de las operaciones. Asegúrese de prestar atención a los paréntesis.
\[\begin{align*} f(x)&= 5{(3)}^{x+1}\\ f(2)&= 5{(3)}^{2+1} \qquad \text{Substitute } x=2\\ &= 5{(3)}^3 \qquad \text{Add the exponents}\\ &= 5(27) \qquad \text{Simplify the power}\\ &= 135 \qquad \text{Multiply} \end{align*}\]
Vamos\(f(x)=8{(1.2)}^{x−5}\). Evaluar\(f(3)\) usando una calculadora. Redondear a cuatro decimales.
- Contestar
-
\(5.5556\)
Definición del crecimiento exponencial
Debido a que la salida de las funciones exponenciales aumenta muy rápidamente, el término “crecimiento exponencial” se usa a menudo en el lenguaje cotidiano para describir cualquier cosa que crece o aumenta rápidamente. Sin embargo, el crecimiento exponencial puede definirse con mayor precisión en un sentido matemático. Si la tasa de crecimiento es proporcional a la cantidad presente, la función modela el crecimiento exponencial.
Una función que modela el crecimiento exponencial crece en una tasa proporcional a la cantidad presente. Para cualquier número real\(x\) y cualquier número real positivo\(a\) y\(b\) tal que\(b≠1\), una función de crecimiento exponencial tenga la forma
\[f(x)=ab^x\]
donde
- \(a\)es el valor inicial o inicial de la función.
- \(b\)es el factor de crecimiento o multiplicador de crecimiento por unidad\(x\).
En términos más generales, tenemos una función exponencial, en la que una base constante se eleva a un exponente variable. Para diferenciar entre funciones lineales y exponenciales, consideremos dos empresas, A y B. La empresa A tiene\(100\) tiendas y se expande abriendo\(50\) nuevas tiendas al año, por lo que su crecimiento puede ser representado por la función\(A(x)=100+50x\). La empresa B tiene\(100\) tiendas y se expande al aumentar el número de tiendas por\(50\%\) cada año, por lo que su crecimiento puede ser representado por la función\(B(x)=100{(1+0.5)}^x\).
En la Tabla se ilustran algunos años de crecimiento para estas empresas\(\PageIndex{3}\).
| Año,\(x\) | Tiendas, Empresa A | Tiendas, Empresa B |
|---|---|---|
| \ (x\) ">\(0\) | \(100+50(0)=100\) | \(100{(1+0.5)}^0=100\) |
| \ (x\) ">\(1\) | \(100+50(1)=150\) | \(100{(1+0.5)}^1=150\) |
| \ (x\) ">\(2\) | \(100+50(2)=200\) | \(100{(1+0.5)}^2=225\) |
| \ (x\) ">\(3\) | \(100+50(3)=250\) | \(100{(1+0.5)}^3=337.5\) |
| \ (x\) ">\(x\) | \(A(x)=100+50x\) | \(B(x)=100{(1+0.5)}^x\) |
En la Figura se muestran las gráficas que comparan el número de tiendas para cada empresa durante un periodo de cinco años\(\PageIndex{2}\). Podemos ver que, con un crecimiento exponencial, el número de tiendas aumenta mucho más rápidamente que con el crecimiento lineal.
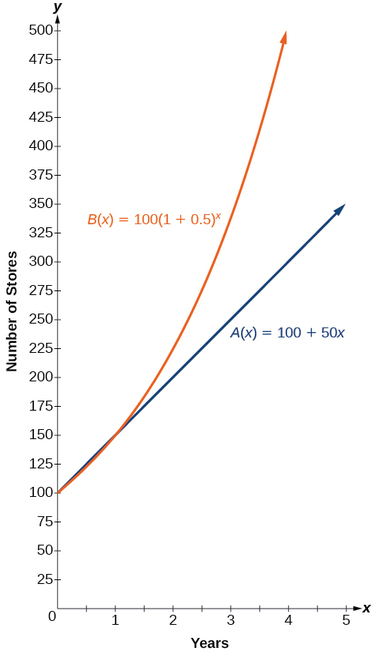
Observe que el dominio para ambas funciones es\([0,\infty)\), y el rango para ambas funciones es\([100,\infty)\). Después del año 1, la Compañía B siempre cuenta con más tiendas que la Compañía A.
Ahora volveremos nuestra atención a la función que representa el número de tiendas para Empresa\(B\),\(B(x)=100{(1+0.5)}^x\). En esta función exponencial,\(100\) representa el número inicial de tiendas,\(0.50\) representa la tasa de crecimiento y\(1+0.5=1.5\) representa el factor de crecimiento. Generalizando más, podemos escribir esta función como\(B(x)=100{(1.5)}^x\), donde\(100\) está el valor inicial,\(1.5\) se llama la base, y\(x\) se llama el exponente.
Al inicio de esta sección, nos enteramos de que la población de la India era de alrededor de\(1.25\) mil millones en el año 2013, con una tasa de crecimiento anual de aproximadamente\(1.2\%\). Esta situación está representada por la función de crecimiento\(P(t)=1.25{(1.012)}^t\), donde\(t\) está el número de años desde 2013. A la milésima más cercana, ¿cuál será la población de la India en 2031?
Solución
Para estimar la población en 2031, evaluamos los modelos para\(t=18\), porque 2031 es\(18\) años después de 2013. Redondeando a la milésima más cercana,
\[P(18)=1.25{(1.012)}^{18}≈1.549 \nonumber\]
Habrá alrededor de\(1.549\) mil millones de personas en la India en el año 2031.
La población de China era de alrededor de\(1.39\) mil millones en el año 2013, con una tasa de crecimiento anual de aproximadamente\(0.6\%\). Esta situación está representada por la función de crecimiento\(P(t)=1.39{(1.006)}^t\), ¿dónde\(t\) está el número de años desde 2013.A la milésima más cercana, cuál será la población de China para el año 2031? ¿Cómo se compara esto con la predicción de población que hicimos para la India en Ejemplo\(\PageIndex{3}\)?
- Contestar
-
Alrededor de\(1.548\) mil millones de personas; para el año 2031, la población de la India superará a la de China en alrededor de\(0.001\) mil millones, o\(1\) millones de personas.
Encontrar ecuaciones de funciones exponenciales
En los ejemplos anteriores, se nos dio una función exponencial, que luego evaluamos para una entrada dada. A veces se nos da información sobre una función exponencial sin conocer la función explícitamente. Debemos usar la información para escribir primero la forma de la función, luego determinar las constantes\(a, a\) y\(b, b\), y evaluar la función.
- Si uno de los puntos de datos tiene la forma\((0,a)\), entonces\(a\) es el valor inicial. Usando\(a\), sustituya el segundo punto en la ecuación\(f(x)=a{(b)}^x\), y resuelva para\(b\).
- Si ninguno de los puntos de datos tiene la forma\((0,a)\), sustituya ambos puntos en dos ecuaciones con la forma\(f(x)=a{(b)}^x\). Resolver el sistema resultante de dos ecuaciones en dos incógnitas para encontrar\(a\) y\(b\).
- Usando el\(a\) y\(b\) que se encuentra en los pasos anteriores, escriba la función exponencial en la forma\(f(x)=a{(b)}^x\).
En 2006, los\(80\) venados fueron introducidos en un refugio de vida silvestre. Para 2012, la población había crecido hasta convertirse en\(180\) ciervos. La población estaba creciendo exponencialmente. Escribir una función algebraica\(N(t)\) que represente la población\((N)\) de ciervos a lo largo del tiempo\(t\).
Solución
Dejamos que nuestra variable independiente\(t\) sea el número de años posteriores a 2006. Así, la información dada en el problema puede escribirse como pares entrada-salida: (0, 80) y (6, 180). Observe que al elegir nuestra variable de entrada para ser medida como años después de 2006, nos hemos dado el valor inicial para la función,\(a=80\). Ahora podemos sustituir el segundo punto en la ecuación\(N(t)=80b^t\) para encontrar\(b\):
\[\begin{align*} N(t)&= 80b^t\\ 180&= 80b^6 \qquad \text{Substitute using point } (6, 180)\\ \dfrac{9}{4}&= b^6 \qquad \text{Divide and write in lowest terms}\\ b&= {\left (\dfrac{9}{4} \right )}^{\tfrac{1}{6}} \qquad \text{Isolate b using properties of exponents}\\ b&\approx 1.1447 \qquad \text{Round to 4 decimal places} \end{align*}\]
A menos que se indique lo contrario, no redondear ningún cálculo intermedio. Después redondear la respuesta final a cuatro lugares para lo que resta de esta sección.
El modelo exponencial para la población de venados es\(N(t)=80{(1.1447)}^t\). (Tenga en cuenta que esta función exponencial modela el crecimiento a corto plazo. A medida que las entradas se hacen grandes, la salida se hará cada vez más grande, tanto es así que el modelo puede no ser útil a largo plazo.)
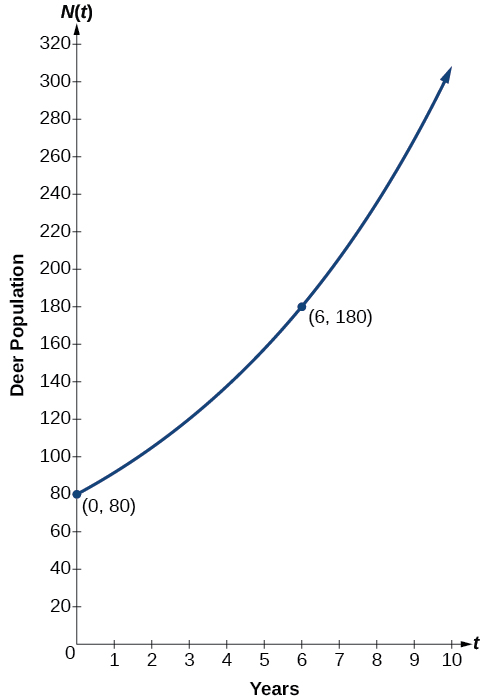
Podemos graficar nuestro modelo para observar el crecimiento poblacional de venados en el refugio a lo largo del tiempo. Observe que la gráfica de la Figura\(\PageIndex{3}\) pasa por los puntos iniciales dados en el problema,\((0, 80)\) y\((6, 180)\). También podemos ver que el dominio para la función es\([0,\infty)\), y el rango para la función es\([80,\infty)\).
Una población de lobos está creciendo exponencialmente. En 2011, se contabilizaron los\(129\) lobos. Para 2013, la población había llegado a los\(236\) lobos. ¿Qué dos puntos se pueden utilizar para derivar una ecuación exponencial modelando esta situación? Escribe la ecuación que representa la población\(N\) de lobos a lo largo del tiempo\(t\).
- Contestar
-
\((0,129)\)y\((2,236)\);\(N(t)=129{(1.3526)}^t\)
Encuentra una función exponencial que pase por los puntos\((−2,6)\) y\((2,1)\).
Solución
Debido a que no tenemos el valor inicial, sustituimos ambos puntos en una ecuación de la forma\(f(x)=ab^x\), y luego resolvemos el sistema para\(a\) y\(b\).
- Sustitución\((−2,6)\) da\(6=ab^{−2}\)
- Sustitución\((2,1)\) da\(1=ab^2\)
Utilice la primera ecuación para resolver\(a\) en términos de\(b\):
\[\begin{align*} 6&= ab^{-2}\\ \dfrac{6}{b^{-2}}&= a \qquad \text{Divide}\\ a&= 6b^2 \qquad \text{Use properties of exponents to rewrite the denominator} \end{align*}\]
Sustituya a en la segunda ecuación, y resuelva por\(b\):
\[\begin{align*} 1&= ab^{2}\\ 1&= 6b^2 b^2\\ &= 6b^4 \qquad \text{Substitute a}\\ b&= \left (\dfrac{1}{6} \right )^{\tfrac{1}{4}} \qquad \text{Round 4 decimal places rewrite the denominator}\\ b&\approx 0.6389 \end{align*}\]
Utilice el valor de\(b\) en la primera ecuación para resolver el valor de\(a\):
\[\begin{align*} a&= 6b^{2}\\ &\approx 6(0.6389)^2 \\ &\approx 2.4492 \end{align*}\]
Así, la ecuación es\(f(x)=2.4492{(0.6389)}^x\).
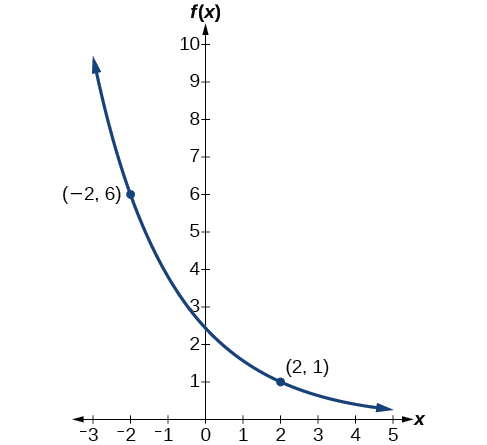
Podemos graficar nuestro modelo para comprobar nuestro trabajo. Observe que la gráfica de la Figura\(\PageIndex{4}\) pasa por los puntos iniciales dados en el problema,\((−2, 6)\) y\((2, 1)\). La gráfica es un ejemplo de una función de decaimiento exponencial.
Dados los dos puntos\((1,3)\) y\((2,4.5)\), encontrar la ecuación de la función exponencial que pasa por estos dos puntos.
- Contestar
-
\(f(x)=2{(1.5)}^x\)
Sí, siempre que los dos puntos estén ambos por encima del eje x o ambos por debajo del eje x y tengan diferentes coordenadas x. Pero hay que tener en cuenta que también necesitamos saber que la gráfica es, de hecho, una función exponencial. No todas las gráficas que se ven exponenciales realmente son exponenciales. Necesitamos saber que la gráfica se basa en un modelo que muestre el mismo porcentaje de crecimiento con cada incremento de unidad en\(x\), que en muchos casos del mundo real implica tiempo.
- Primero, identificar dos puntos en la gráfica. Elija la\(y\) -intercepción como uno de los dos puntos siempre que sea posible. Trate de elegir puntos que estén lo más separados posible para reducir el error de redondeo.
- Si uno de los puntos de datos es el\(y\) -intercept\((0,a)\), entonces\(a\) es el valor inicial. Usando\(a\), sustituya el segundo punto en la ecuación\(f(x)=a{(b)}^x\) y resuelva por\(b\)
- Si ninguno de los puntos de datos tiene la forma\((0,a)\), sustituya ambos puntos en dos ecuaciones con la forma\(f(x)=a{(b)}^x\). Resolver el sistema resultante de dos ecuaciones en dos incógnitas para encontrar\(a\) y\(b\).
- Escribe la función exponencial,\(f(x)=a{(b)}^x\).
Encuentre una ecuación para la función exponencial graficada en la Figura\(\PageIndex{5}\).
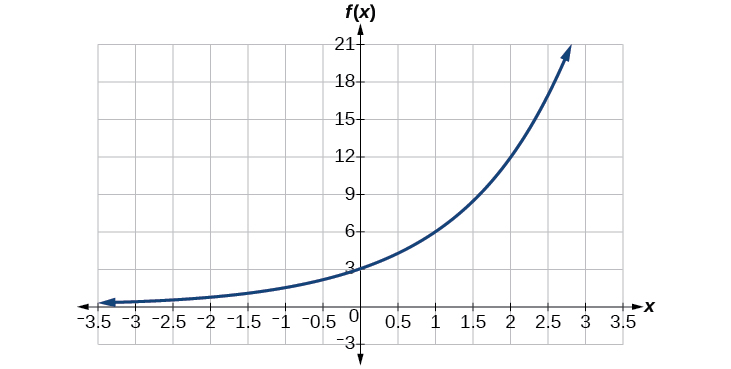
Solución
Podemos elegir la \(y\)-intercepción de la gráfica,\((0,3)\), como nuestro primer punto. Esto nos da el valor inicial,\(a=3\). A continuación, elija un punto en la curva a cierta distancia de\((0,3)\) que tenga coordenadas enteras. Uno de esos puntos es\((2,12)\).
\[\begin{align*} y&= ab^x \qquad \text{Write the general form of an exponential equation}\\ y&= 3b^x \qquad \text{Substitute the initial value } 3 \text{ for } a\\ 12&= 3b^2 \qquad \text{Substitute in 12 for } y \text{ and } 2 \text{ for } x\\ 4&= b^2 \qquad \text{Divide by }3\\ b&= \pm 2 \qquad \text{Take the square root} \end{align*}\]
Porque nos limitamos a valores positivos de\(b\), vamos a utilizar\(b=2\). Sustituir\(a\) y\(b\) en la forma estándar para producir la ecuación\(f(x)=3{(2)}^x\).
Encuentre una ecuación para la función exponencial graficada en la Figura\(\PageIndex{6}\).
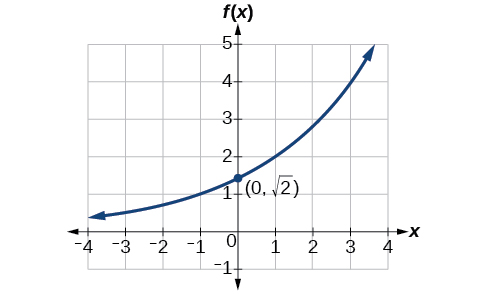
- Contestar
-
\(f(x)=\sqrt{2}{(\sqrt{2})}^x\). Las respuestas pueden variar debido a un error de redondeo. La respuesta debe ser muy cercana a\(1.4142{(1.4142)}^x\).
- Presione [STAT].
- Borre todas las entradas existentes en las columnas L1 o L2.
- En L1, ingrese las coordenadas x dadas.
- En L2, ingrese las coordenadas y correspondientes.
- Presione [STAT] nuevamente. Cursor a la derecha a CALC, desplácese hacia abajo hasta ExpreG (Regresión Exponencial) y presione [ENTRAR].
- La pantalla muestra los valores de a y b en la ecuación exponencial\(y=a⋅b^x\).
Utilice una calculadora gráfica para encontrar la ecuación exponencial que incluye los puntos\((2,24.8)\) y\((5,198.4)\).
Solución
Siga las pautas anteriores. Primero presione [STAT], [EDITAR], [1: Editar...], y borre las listas L1 y L2. A continuación, en la columna L1, ingrese las\(x\) coordenadas\(2\) -y\(5\). Haga lo mismo en la columna L2 para las\(y\) coordenadas\(24.8\) -y\(198.4\).
Ahora pulse [STAT], [CALC], [0: ExPrEg] y pulse [ENTER]. Los valores\(a=6.2\) y se\(b=2\) mostrarán. La ecuación exponencial es\(y=6.2⋅2^x\).
Utilice una calculadora gráfica para encontrar la ecuación exponencial que incluye los puntos\((3, 75.98)\) y\((6, 481.07)\).
- Contestar
-
\(y≈12⋅{1.85}^x\)
Aplicación de la fórmula de interés compuesto
Los instrumentos de ahorro en los que las ganancias se reinvierten continuamente, como los fondos mutuos y las cuentas de jubilación, utilizan intereses compuestos. El término compuesto se refiere a los intereses devengados no sólo sobre el valor original, sino sobre el valor acumulado de la cuenta.
La tasa porcentual anual (TAE) de una cuenta, también llamada tasa nominal, es la tasa de interés anual ganada por una cuenta de inversión. El término nominal se utiliza cuando la composición ocurre varias veces distintas de una vez al año. De hecho, cuando el interés se agrava más de una vez al año, ¡la tasa de interés efectiva termina siendo mayor que la tasa nominal! Esta es una herramienta poderosa para invertir.
Podemos calcular el interés compuesto usando la fórmula de interés compuesto, que es una función exponencial de las variables tiempo\(t\)\(P\)\(APR\)\(r\), principal y número de períodos compuestos en un año\(n\):
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt} \nonumber\]
Por ejemplo, observe Tabla\(\PageIndex{4}\), que muestra el resultado de invertir\($1,000\) en\(10\%\) por un año. Observe cómo aumenta el valor de la cuenta a medida que aumenta la frecuencia de composición.
| Frecuencia | Valor después del\(1\) año |
|---|---|
| Anualmente | \ (1\) año">\($1100\) |
| Semestralmente | \ (1\) año">\($1102.50\) |
| Trimestral | \ (1\) año">\($1103.81\) |
| Mensual | \ (1\) año">\($1104.71\) |
| Diario | \ (1\) año">\($1105.16\) |
El interés compuesto se puede calcular usando la fórmula
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt}\]
donde
- \(A(t)\)es el valor de la cuenta,
- \(t\)se mide en años,
- \(P\)es el monto inicial de la cuenta, a menudo llamado principal, o más generalmente valor presente,
- \(r\)es la tasa porcentual anual (TAE) expresada como decimal, y
- \(n\)es el número de períodos compuestos en un año.
Si invertimos\($3,000\) en una cuenta de inversión pagando\(3\%\) intereses compuestos trimestralmente, ¿cuánto valdrá la cuenta en\(10\) años?
Solución
Porque estamos empezando con\($3,000\),\(P=3000\). Nuestra tasa de interés es\(3\%\), entonces\(r = 0.03\). Debido a que estamos componiendo trimestralmente, estamos componiendo\(4\) tiempos al año, entonces\(n=4\). Queremos conocer el valor de la cuenta en\(10\) años, así que estamos buscando\(A(10)\), el valor cuando\(t = 10\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ A(10)&= 3000{\left (1+\dfrac{0.03}{4} \right )}^{(4)\cdot (10)} \qquad \text{Substitute using given values}\\ &\approx \$4045.05 \qquad \text{Round to two decimal places} \end{align*}\]
La cuenta valdrá aproximadamente\($4,045.05\) en\(10\) años.
Una inversión inicial de\($100,000\)\(12\%\) interés se compone semanalmente (\(52\)semanas de uso en un año). ¿Cuál será el valor de la inversión en\(30\) años?
- Contestar
-
acerca de\($3,644,675.88\)
Un Plan 529 es un plan de ahorro universitario que permite a los familiares invertir dinero para pagar la futura matrícula universitaria de un niño; la cuenta crece libre de impuestos. Lily quiere establecer una cuenta 529 para su nueva nieta y quiere que la cuenta crezca a\($40,000\) lo largo de los\(18\) años. Ella cree que la cuenta ganará\(6\%\) compuesto semestralmente (dos veces al año). Al dólar más cercano, ¿cuánto necesitará Lily para invertir en la cuenta ahora?
Solución
La tasa de interés nominal es\(6\%\), entonces\(r=0.06\). El interés se agrava dos veces al año, entonces\(k=2\).
Queremos encontrar la inversión inicial,\(P\), necesaria para que el valor de la cuenta valga\($40,000\) en\(18\) años. Sustituir los valores dados en la fórmula de interés compuesto, y resolver para\(P\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ 40,000&= P{\left (1+\dfrac{0.06}{2} \right )}^{2(18)} \qquad \text{Substitute using given values } A, r, n, t\\ 40,000&= P{(1.03)}^{36} \qquad \text{Simplify}\\ \dfrac{40,000}{ {(1.03)}^{36} }&= P \qquad \text{Isolate } P\\ P&\approx \$13,801 \qquad \text{Divide and round to the nearest dollar} \end{align*}\]
Lily necesitará invertir para\($13,801\) tener\($40,000\) en\(18\) años.
Refiérase a Ejemplo\(\PageIndex{9}\). Al dólar más cercano, ¿cuánto necesitaría invertir Lily si la cuenta se compone trimestralmente?
- Contestar
-
\($13,693\)
Evaluación de funciones con Base\(e\)
Como vimos anteriormente, la cantidad ganada en una cuenta aumenta a medida que aumenta la frecuencia de composición. El cuadro\(\PageIndex{5}\) muestra que el incremento de la composición anual a semestral es mayor que el incremento de la composición mensual a la diaria. Esto podría llevarnos a preguntarnos si este patrón continuará.
Examinar el valor de los\($1\) invertidos a\(100\%\) interés por\(1\) año, compuesto en diversas frecuencias, listado en la Tabla\(\PageIndex{5}\).
| Frecuencia | \(A(t)={\left (1+\dfrac{1}{n} \right )}^n\) | Valor |
|---|---|---|
| Anualmente | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{1} \right )}^1\) | \($2\) |
| Semestralmente | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{2} \right )}^2\) | \($2.25\) |
| Trimestral | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{4} \right )}^4\) | \($2.441406\) |
| Mensual | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{12} \right )}^{12}\) | \($2.613035\) |
| Diario | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{365} \right )}^{365}\) | \($2.714567\) |
| Por hora | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{8760} \right )}^{8760}\) | \($2.718127\) |
| Una vez por minuto | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{525600} \right )}^{525600}\) | \($2.718279\) |
| Una vez por segundo | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="vertical-align:middle; ">\({\left (1+\dfrac{1}{31536000} \right )}^{31536000}\) | \($2.718282\) |
Estos valores parecen estar acercándose a un límite a medida que\(n\) aumenta sin límite. De hecho, a medida que\(n\) se hace cada vez más grande, la expresión se\({\left (1+\dfrac{1}{n} \right )}^n\) acerca a un número usado con tanta frecuencia en matemáticas que tiene su propio nombre: la letra\(e\). Este valor es un número irracional, lo que significa que su expansión decimal continúa para siempre sin repetirse. Su aproximación a seis decimales se muestra a continuación.
La letra\(e\) representa el número irracional
\[{\left (1+\dfrac{1}{n} \right )}^n\]
a medida que\(n\) aumenta sin ataduras
La letra\(e\) se utiliza como base para muchos modelos exponenciales del mundo real. Para trabajar con base\(e\), utilizamos la aproximación,\(e≈2.718282\). La constante fue nombrada por el matemático suizo Leonhard Euler (1707—1783) quien primero investigó y descubrió muchas de sus propiedades.
Calcular\(e^{3.14}\). Redondear a cinco decimales.
Solución
En una calculadora, presione el botón etiquetado\([e^x]\). La ventana muestra\([e {}^( ]\). Escriba\(3.14\) y luego cierre paréntesis,\([)]\). Pulse [ENTER]. Redondeo a\(5\) decimales,\(e^{3.14}≈23.10387\). Precaución: Muchas calculadoras científicas tienen un botón “Exp”, que se utiliza para ingresar números en notación científica. No se utiliza para encontrar poderes de\(e\).
Usa una calculadora para encontrar\(e^{−0.5}\). Redondear a cinco decimales.
- Contestar
-
\(e^{−0.5}≈0.60653\)
Investigar el crecimiento continuo
Hasta el momento hemos trabajado con bases racionales para funciones exponenciales. Para la mayoría de los fenómenos del mundo real, sin embargo,\(e\) se utiliza como base para funciones exponenciales. Los modelos exponenciales que utilizan\(e\) como base se denominan modelos de crecimiento continuo o decaimiento. Vemos estos modelos en las finanzas, la informática y la mayoría de las ciencias, como la física, la toxicología y la dinámica de fluidos.
Para todos los números reales\(t\), y todos los números positivos\(a\) y\(r\), el crecimiento continuo o decaimiento se representa por la fórmula
\[A(t)=ae^{rt}\]
donde
- \(a\)es el valor inicial,
- \(r\)es la tasa de crecimiento continuo por unidad de tiempo,
- \(t\)es el tiempo transcurrido.
Si\(r>0\), entonces la fórmula representa un crecimiento continuo. Si\(r<0\), entonces la fórmula representa decaimiento continuo.
Para aplicaciones empresariales, la fórmula de crecimiento continuo se llama fórmula de composición continua y toma la forma
\[A(t)=Pe^{rt}\]
donde
- \(P\)es el principal o el inicial invertido,
- \(r\)es el crecimiento o tasa de interés por unidad de tiempo,
- \(t\)es el periodo o plazo de la inversión.
- Utilice la información en el problema para determinar\(a\), el valor inicial de la función.
- Utilice la información del problema para determinar la tasa de crecimiento\(r\).
- Si el problema se refiere al crecimiento continuo, entonces\(r>0\).
- Si el problema se refiere a decaimiento continuo, entonces\(r<0\).
- Utilice la información en el problema para determinar el tiempo\(t\).
- Sustituir la información dada en la fórmula de crecimiento continuo y resolver para\(A(t)\).
Una persona invirtió\($1,000\) en una cuenta ganando un valor nominal\(10\%\) por año agravado continuamente. ¿Cuánto había en la cuenta al cierre de un año?
Solución
Dado que la cuenta está creciendo en valor, este es un problema continuo de composición con la tasa de crecimiento\(r=0.10\). La inversión inicial fue\($1,000\), entonces\(P=1000\). Utilizamos la fórmula de composición continua para encontrar el valor tras\(t=1\) año:
\[\begin{align*} A(t)&= Pe^{rt} \qquad \text{Use the continuous compounding formula}\\ &= 1000{(e)}^{0.1} \qquad \text{Substitute known values for } P, r, t\\ &\approx 1105.17 \qquad \text{Use a calculator to approximate} \end{align*}\]
La cuenta vale\($1,105.17\) después de un año.
Una persona invierte\($100,000\) a un\(12\%\) interés nominal por año compuesto continuamente. ¿Cuál será el valor de la inversión en\(30\) años?
- Contestar
-
\($3,659,823.44\)
\(Radon-222\)decae a una tasa continua de\(17.3\%\) por día. ¿A cuánta voluntad\(100 mg\) de\(Radon-222\) decaimiento en\(3\) días?
Solución
Dado que la sustancia está en descomposición, la tasa,\(17.3\%\), es negativa. Entonces,\(r = −0.173\). La cantidad inicial de\(Radon-222\) fue\(100\) mg, entonces\(a=100\). Utilizamos la fórmula de decaimiento continuo para encontrar el valor después de\(t=3\) días:
\[\begin{align*} A(t)&= ae^{rt} \qquad \text{Use the continuous growth formula}\\ &= 100e6{-0.173(3)} \qquad \text{Substitute known values for } a, r, t\\ &\approx 59.5115 \qquad \text{Use a calculator to approximate} \end{align*}\]
Entonces\(59.5115\) mg de\(Radon-222\) quedarán.
Usando los datos de Ejemplo\(\PageIndex{12}\), ¿cuánto\(Radon-222\) quedará después de un año?
- Contestar
-
\(3.77E-26\)(Esta es la notación de calculadora para el número escrito como\(3.77×10^{−26}\) en notación científica. Si bien la salida de una función exponencial nunca es cero, este número está tan cerca de cero que para todos los fines prácticos podemos aceptar cero como respuesta.)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con funciones exponenciales.
- Función de crecimiento exponencial
- Interés Compuesto
Ecuaciones Clave
| definición de la función exponencial | \(f(x)=b^x\), donde\(b>0\),\(b≠1\) |
| definición de crecimiento exponencial | \(f(x)=ab^x\), donde\(a>0\)\(b>0\),\(b≠1\) |
| fórmula de interés compuesto |
\(A(t)=P{(1+\dfrac{r}{n})}^{nt}\), dónde\(A(t)\) está el valor de la cuenta en el momento\(t\) \(t\)es el número de años \(P\)es la inversión inicial, a menudo llamada el principal \(r\)es la tasa porcentual anual (TAE), o tasa nominal \(n\)es el número de períodos compuestos en un año |
| fórmula de crecimiento continuo | \(A(t)=ae^{rt}\), donde\(t\) es el número de periodos de tiempo unitarios de crecimiento\(a\) es la cantidad inicial (en la fórmula compuesta continua a se sustituye por\(P\), el principal)\(e\) es la constante matemática,\(e≈2.718282\) |
Conceptos clave
- Una función exponencial se define como una función con una constante positiva distinta de\(1\) elevada a un exponente variable. Ver Ejemplo.
- Una función se evalúa resolviendo a un valor específico. Ver Ejemplo y Ejemplo.
- Se puede encontrar un modelo exponencial cuando se conoce la tasa de crecimiento y el valor inicial. Ver Ejemplo.
- Se puede encontrar un modelo exponencial cuando se conocen los dos puntos de datos del modelo. Ver Ejemplo.
- Se puede encontrar un modelo exponencial utilizando dos puntos de datos de la gráfica del modelo. Ver Ejemplo.
- Se puede encontrar un modelo exponencial utilizando dos puntos de datos de la gráfica y una calculadora. Ver Ejemplo.
- El valor de una cuenta en cualquier momento se\(t\) puede calcular utilizando la fórmula de interés compuesto cuando se conocen el principal, la tasa de interés anual y los períodos compuestos. Ver Ejemplo.
- La inversión inicial de una cuenta se puede encontrar utilizando la fórmula de interés compuesto cuando se conoce el valor de la cuenta, la tasa de interés anual, los períodos de capitalización y la vida útil de la cuenta. Ver Ejemplo.
- El número\(e\) es una constante matemática utilizada a menudo como base de modelos de crecimiento exponencial y decaimiento del mundo real. Su aproximación decimal es\(e≈2.718282\).
- Las calculadoras científicas y gráficas tienen la clave\([ex]\) o\([exp(x)]\) para calcular los poderes de\(e\). Ver Ejemplo.
- Los modelos de crecimiento continuo o decaimiento son modelos exponenciales que utilizan\(e\) como base. Los modelos de crecimiento continuo y decaimiento se pueden encontrar cuando se conoce el valor inicial y la tasa de crecimiento o decaimiento. Ver Ejemplo y Ejemplo.


