6.8: Crecimiento y Decaimiento Exponencial
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Utilizar el modelo de crecimiento exponencial en aplicaciones, incluyendo crecimiento poblacional e interés compuesto.
- Explicar el concepto de duplicar el tiempo.
- Utilice el modelo de decaimiento exponencial en aplicaciones, incluyendo la desintegración radiactiva y la ley de enfriamiento de Newton.
- Explicar el concepto de vida media.
Una de las aplicaciones más prevalentes de las funciones exponenciales involucra modelos de crecimiento y decaimiento. El crecimiento exponencial y el decaimiento aparecen en multitud de aplicaciones naturales. Desde el crecimiento de la población y el interés continuamente compuesto hasta la desintegración radiactiva y la ley de enfriamiento de Newton, las funciones exponenciales son ubicuas en la naturaleza. En esta sección, examinamos el crecimiento exponencial y la decadencia en el contexto de algunas de estas aplicaciones.
Modelo de Crecimiento Exponencial
Muchos sistemas exhiben un crecimiento exponencial. Estos sistemas siguen un modelo de la formay=y_0e^{kt}, dondey_0 representa el estado inicial del sistema yk es una constante positiva, llamada constante de crecimiento. Observe que en un modelo de crecimiento exponencial, tenemos
y′=ky_0e^{kt}=ky. \label{eq1}
Es decir, la tasa de crecimiento es proporcional al valor de la función actual. Esta es una característica clave del crecimiento exponencial. La ecuación\ ref {eq1} implica derivadas y se denomina ecuación diferencial.
Sistemas que exhiben incremento exponencial de crecimiento según el modelo matemático
y=y_0e^{kt} \nonumber
dondey_0 representa el estado inicial del sistema yk>0 es una constante, llamada constante de crecimiento.
El crecimiento poblacional es un ejemplo común de crecimiento exponencial. Considera una población de bacterias, por ejemplo. Parece plausible que la tasa de crecimiento poblacional sea proporcional al tamaño de la población. Después de todo, cuantas más bacterias haya para reproducirse, más rápido crece la población. La Figura\PageIndex{1} y la Tabla\PageIndex{1} representan el crecimiento de una población de bacterias con una población inicial de 200 bacterias y una constante de crecimiento de 0.02. Observe que después de solo 2 horas (120 minutos), ¡la población es 10 veces su tamaño original!
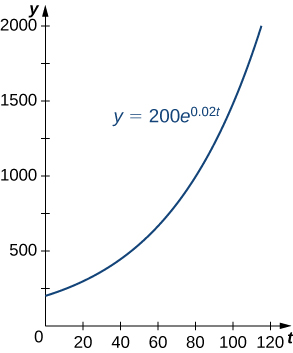
| Tiempo (min) | Tamaño de la población (no. de bacterias) |
|---|---|
| 10 | 244 |
| 20 | 298 |
| 30 | 364 |
| 40 | 445 |
| 50 | 544 |
| 60 | 664 |
| 70 | 811 |
| 80 | 991 |
| 90 | 1210 |
| 100 | 1478 |
| 110 | 1805 |
| 120 | 2205 |
Tenga en cuenta que estamos usando una función continua para modelar lo que es un comportamiento inherentemente discreto. En cualquier momento dado, la población del mundo real contiene un número entero de bacterias, aunque el modelo adquiere valores no enteros. Al usar modelos de crecimiento exponencial, siempre debemos tener cuidado de interpretar los valores de las funciones en el contexto del fenómeno que estamos modelando.
Considerar la población de bacterias descrita anteriormente. Esta población crece de acuerdo a la funciónf(t)=200e^{0.02t}, donde t se mide en minutos. ¿Cuántas bacterias están presentes en la población después de5 horas (300minutos)? ¿Cuándo llega la población a100,000 las bacterias?
Solución
Tenemosf(t)=200e^{0.02t}. Entonces
f(300)=200e^{0.02(300)}≈80,686. \nonumber
Hay80,686 bacterias en la población después de5 horas.
Para encontrar cuándo la población alcanza100,000 bacterias, resolvemos la ecuación
\begin{align*} 100,000 &= 200e^{0.02t} \\[4pt] 500 &=e^{0.02t} \\[4pt] \ln 500 &=0.02 t \\[4pt] t &=\frac{\ln 500}{0.02}≈310.73. \end{align*} \nonumber
La población llega a100,000 las bacterias después de310.73 minutos.
Considera una población de bacterias que crece de acuerdo a la funciónf(t)=500e^{0.05t}, dondet se mide en minutos. ¿Cuántas bacterias están presentes en la población después de las 4 horas? ¿Cuándo llega la población a100 millones de bacterias?
- Contestar
-
Utilice el proceso del ejemplo anterior.
- Contestar
-
Hay81,377,396 bacterias en la población después de4 horas. La población alcanza100 millones de bacterias después de244.12 minutos.
Ahora volvamos nuestra atención a una aplicación financiera: el interés compuesto. El interés que no se compone se llama interés simple. Los intereses simples se pagan una vez, al término del período de tiempo especificado (generalmente1 año). Entonces, si ponemos$1000 en una cuenta de ahorro ganando intereses2% simples por año, entonces al final del año tenemos
1000(1+0.02)=$1020. \nonumber
Los intereses compuestos se pagan varias veces al año, dependiendo del período compuesto. Por lo tanto, si el banco compone los intereses cada6 mes, acredita la mitad de los intereses del año a la cuenta después de6 meses. Durante el segundo semestre del año, la cuenta gana intereses no sólo sobre el inicial$1000, sino también sobre los intereses devengados durante el primer semestre del año. Matemáticamente hablando, al final del año, tenemos
1000 \left(1+\dfrac{0.02}{2}\right)^2=$1020.10. \nonumber
De igual manera, si el interés se agrava cada4 mes, tenemos
1000 \left(1+\dfrac{0.02}{3}\right)^3=$1020.13, \nonumber
y si el interés se compone diariamente (365veces al año), tenemos$1020.20. Si ampliamos este concepto, para que el interés se agrava continuamente, después det años tenemos
1000\lim_{n→∞} \left(1+\dfrac{0.02}{n}\right)^{nt}. \nonumber
Ahora manipulemos esta expresión para que tengamos una función de crecimiento exponencial. Recordemos que el número see puede expresar como un límite:
e=\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m. \nonumber
En base a esto, queremos que la expresión dentro de los paréntesis tenga la forma(1+1/m). Vamosn=0.02m. Tenga en cuentan→∞, m→∞ que también. Entonces conseguimos
1000\lim_{n→∞}\left(1+\dfrac{0.02}{n}\right)^{nt}=1000\lim_{m→∞}\left(1+\dfrac{0.02}{0.02m}\right)^{0.02mt}=1000\left[\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m\right]^{0.02t}. \nonumber
Reconocemos el límite dentro de los corchetes como el númeroe. Entonces, el saldo en nuestra cuenta bancaria después det años viene dado por1000 e^{0.02t}. Generalizando este concepto, vemos que si una cuenta bancaria con saldo inicial de$P gana intereses a una tasa der%, compuesta continuamente, entonces el saldo de la cuenta después det años es
\text{Balance}\;=Pe^{rt}. \nonumber
A un estudiante de 25 años se le ofrece la oportunidad de invertir algo de dinero en una cuenta de retiro que paga intereses5% anuales compuestos continuamente. ¿Cuánto necesita invertir la estudiante hoy para tener$1 millones cuando se jubila a la edad65? ¿Y si pudiera ganar intereses6% anuales compuestos continuamente en su lugar?
Solución
Tenemos
1,000,000=Pe^{0.05(40)} \nonumber
P=135,335.28. \nonumber
Ella debe invertir$135,335.28 a5% intereses.
Si, en cambio, ella es capaz de ganar6%, entonces la ecuación se convierte
1,000,000=Pe^{0.06(40)} \nonumber
P=90,717.95. \nonumber
En este caso, solo necesita invertir$90,717.95. Esto es aproximadamente dos tercios de la cantidad en la que necesita invertir5%. El hecho de que el interés se compense continuamente magnifica enormemente el efecto del1% incremento de la tasa de interés.
Supongamos que en lugar de invertir a la edad25\sqrt{b^2−4ac}, el estudiante espera hasta la edad35. ¿En cuánto tendría que invertir5%? 6%¿A?
- Pista
-
Utilice el proceso del ejemplo anterior.
- Contestar
-
A5% los intereses, debe invertir$223,130.16. A6% intereses, debe invertir$165,298.89.
Si una cantidad crece exponencialmente, el tiempo que tarda en duplicarse la cantidad permanece constante. En otras palabras, se necesita la misma cantidad de tiempo para que una población de bacterias crezca de100 a200 bacterias que a crecer de10,000 a20,000 bacterias. Esta vez se llama el tiempo de duplicación. Para calcular el tiempo de duplicación, queremos saber cuándo la cantidad alcanza el doble de su tamaño original. Así que tenemos
\begin{align*} 2y_0 &=y_0e^{kt} \\[4pt] 2 &=e^{kt} \\[4pt] \ln 2 &=kt \\[4pt] t &=\dfrac{\ln 2}{k}. \end{align*} \nonumber
Si una cantidad crece exponencialmente, el tiempo de duplicación es la cantidad de tiempo que tarda la cantidad en duplicarse. Está dado por
\text{Doubling time}=\dfrac{\ln 2}{k}. \nonumber
Supongamos que una población de peces crece exponencialmente. Un estanque se abastece inicialmente con500 peces. Después de6 meses, hay1000 peces en el estanque. El dueño permitirá que sus amigos y vecinos pesquen en su estanque después de que llegue la población de peces10,000. ¿Cuándo se permitirá pescar a los amigos del dueño?
Solución
Sabemos que la población de peces tarda6 meses en duplicar su tamaño. Entonces, sit representa tiempo en meses, por la fórmula de doble tiempo, tenemos6=(\ln 2)/k. Entonces,k=(\ln 2)/6. Así, la población está dada pory=500e^{((\ln 2)/6)t}. Para averiguar cuándo llega la población a los10,000 peces, debemos resolver la siguiente ecuación:
\begin{align*} 10,000 &=500e^{(\ln 2/6)t} \\[4pt] 20 &=e^{(\ln 2/6)t} \\[4pt] \ln 20 &=\left(\frac{\ln 2}{6}\right)t \\[4pt] t &=\frac{6(\ln 20)}{\ln 2} \\[4pt] &≈25.93. \end{align*} \nonumber
Los amigos del dueño tienen que esperar25.93 meses (un poco más de2 años) para pescar en el estanque.
Supongamos que la población de peces en Ejemplo tarda9 meses en llegar\PageIndex{3} a1000 los peces. En estas circunstancias, ¿cuánto tiempo tienen que esperar los amigos del dueño?
- Pista
-
Utilice el proceso del ejemplo anterior.
- Contestar
-
38.90meses
Modelo de decaimiento exponencial
Las funciones exponenciales también se pueden usar para modelar poblaciones que se encogen (de enfermedades, por ejemplo), o compuestos químicos que se descomponen con el tiempo. Decimos que tales sistemas exhiben decaimiento exponencial, más que crecimiento exponencial. El modelo es casi el mismo, excepto que hay un signo negativo en el exponente. Así, para alguna constante positivak, tenemos
y=y_0e^{−kt}. \nonumber
Al igual que con el crecimiento exponencial, existe una ecuación diferencial asociada a la decadencia exponencial. Tenemos
y′=−ky_0e^{−kt}=−ky. \nonumber
Los sistemas que exhiben decaimiento exponencial se comportan de acuerdo con el modelo
y=y_0e^{−kt}, \nonumber
dondey_0 representa el estado inicial del sistema yk>0 es una constante, llamada constante de decaimiento.
La figura\PageIndex{2} muestra una gráfica de una función de decaimiento exponencial representativa.
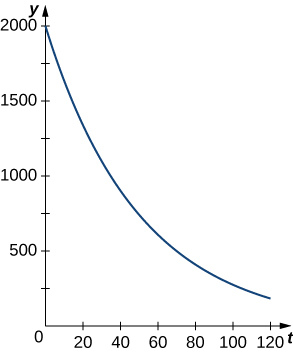
Veamos una aplicación física de decaimiento exponencial. La ley de enfriamiento de Newton dice que un objeto se enfría a una velocidad proporcional a la diferencia entre la temperatura del objeto y la temperatura del entorno. En otras palabras, siT representa la temperatura del objeto yT_a representa la temperatura ambiente en una habitación, entonces
T′=−k(T−T_a). \nonumber
Tenga en cuenta que este no es del todo el modelo adecuado para la decadencia exponencial. Queremos que la derivada sea proporcional a la función, y esta expresión tiene elT_a término adicional. Afortunadamente, podemos hacer un cambio de variables que resuelva este problema. Vamosy(t)=T(t)−T_a. Entoncesy′(t)=T′(t)−0=T′(t), y nuestra ecuación se convierte
y′=−ky. \nonumber
De nuestro trabajo anterior, sabemos que esta relación entrey y su derivada conduce a una decadencia exponencial. Por lo tanto,
y=y_0e^{−kt}, \nonumber
y vemos que
T−T_a=(T_0−T_a)e^{−kt} \nonumber
T=(T_0−T_a)e^{−kt}+T_a \nonumber
dondeT_0 representa la temperatura inicial. Apliquemos esta fórmula en el siguiente ejemplo.
Según baristas experimentados, la temperatura óptima para servir café es entre155°F y175°F. Supongamos que el café se vierte a una temperatura de200°F, y después de2 minutos en una70°F habitación se ha enfriado a180°F. ¿Cuándo es el café lo suficientemente frío como para servirlo? ¿Cuándo el café está demasiado frío para servirlo? Respuestas redondas al medio minuto más cercano.
Solución
Tenemos
\begin{align*} T &=(T_0−T_a)e^{−kt}+T_a \\[4pt] 180 &=(200−70)e^{−k(2)}+70 \\[4pt] 110 &=130e^{−2k} \\[4pt] \dfrac{11}{13} &=e^{−2k} \\[4pt] \ln \dfrac{11}{13} &=−2k \\[4pt] \ln 11−\ln 13 &=−2k \\[4pt] k &=\dfrac{\ln 13−\ln 11}{2} \end{align*}
Entonces, el modelo es
T=130e^{(\ln 11−\ln 13/2)t}+70. \nonumber
El café llega175°F cuando
\begin{align*} 175 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt]105 &=130e^{(\ln 11−\ln 13/2)t} \\[4pt] \dfrac{21}{26} &=e^{(\ln 11−\ln 13/2)t} \\[4pt] \ln \dfrac{21}{26} &=\dfrac{\ln 11−\ln 13}{2}t \\[4pt] \ln 21−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 21−\ln 26)}{\ln 11−\ln 13}\\[4pt] &≈2.56. \end{align*}
El café se puede servir unos2.5 minutos después de que se vierte. El café llega155°F a
\begin{align*} 155 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt] 85 &=130e^{(\ln 11−\ln 13)t} \\[4pt] \dfrac{17}{26} &=e^{(\ln 11−\ln 13)t} \\[4pt] \ln 17−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 17−\ln 26)}{\ln 11−\ln 13} \\[4pt] &≈5.09.\end{align*}
El café está demasiado frío para servirlo unos5 minutos después de que se vierte.
Supongamos que la habitación es más cálida(75°F) y, después de2 minutos, el café se ha enfriado solo a185°F. ¿Cuándo el café primero está lo suficientemente frío como para servirlo? ¿Cuándo el café está demasiado frío para servirlo? Respuestas redondas al medio minuto más cercano.
- Pista
-
Utilice el proceso del ejemplo anterior.
- Contestar
-
El café es primero lo suficientemente frío como para servir unos3.5 minutos después de que se vierte. El café está demasiado frío para servir unos7 minutos después de que se vierte.
Así como los sistemas que exhiben crecimiento exponencial tienen un tiempo de duplicación constante, los sistemas que exhiben decaimiento exponencial tienen una vida media constante. Para calcular la vida media, queremos saber cuándo la cantidad alcanza la mitad de su tamaño original. Por lo tanto, tenemos
\dfrac{y_0}{2}=y_0e^{−kt}
\dfrac{1}{2}=e^{−kt}
−\ln 2=−kt
t=\dfrac{\ln 2}{k}.
Nota: Esta es la misma expresión que se nos ocurrió para duplicar el tiempo.
Si una cantidad decae exponencialmente, la vida media es la cantidad de tiempo que tarda la cantidad en reducirse a la mitad. Está dado por
\text{Half-life}=\dfrac{\ln 2}{k}. \nonumber
Una de las aplicaciones más comunes de un modelo de decaimiento exponencial es la datación por carbono. El carbono-14 se descompone (emite una partícula radiactiva) a una velocidad exponencial regular y consistente. Por lo tanto, si sabemos cuánto carbono-14 estaba originalmente presente en un objeto y cuánto carbono-14 queda, podemos determinar la edad del objeto. La vida media del carbono-14 es de aproximadamente 5730 años, es decir, después de tantos años, la mitad del material se ha convertido del carbono-14 original al nuevo nitrógeno-14 no radiactivo. Si hoy tenemos 100 g de carbono-14, ¿cuánto queda en 50 años? Si un artefacto que originalmente contenía 100 g de carbono-14 ahora contiene 10 g de carbono-14, ¿qué edad tiene? Redondear la respuesta a los cien años más cercanos.
Solución
Tenemos
5730=\dfrac{\ln 2}{k} \nonumber
k=\dfrac{\ln 2}{5730}.\nonumber
Entonces, el modelo dice
y=100e^{−(\ln 2/5730)t}.\nonumber
En50 años, tenemos
y=100e^{−(\ln 2/5730)(50)}≈99.40\nonumber
Por lo tanto, en50 años, queda99.40 g de carbono-14.
Para determinar la edad del artefacto, debemos resolver
\begin{align*} 10 &=100e^{−(\ln 2/5730)t} \\[4pt] \dfrac{1}{10} &= e^{−(\ln 2/5730)t} \\ t &≈19035. \end{align*}
El artefacto tiene aproximadamente19,000 años.
Si tenemos 100 g de carbono-14 , cuanto queda después de 500 años? Si un artefacto que originalmente contenía 100 g de carbono-14 ahora contiene 20 g de carbono-14, ¿cuántos años tiene? Redondear la respuesta a los cien años más cercanos.
- Pista
-
Utilice el proceso del ejemplo anterior.
- Contestar
-
Un total de 94.13 g de carbono-14 permanece después de 500 años. El artefacto tiene aproximadamente 13.300 años de antigüedad.
Conceptos clave
- El crecimiento exponencial y la decadencia exponencial son dos de las aplicaciones más comunes de las funciones exponenciales.
- Los sistemas que exhiben crecimiento exponencial siguen un modelo de la formay=y_0e^{kt}.
- En crecimiento exponencial, la tasa de crecimiento es proporcional a la cantidad presente. En otras palabras,y′=ky.
- Los sistemas que exhiben crecimiento exponencial tienen un tiempo de duplicación constante, el cual viene dado por(\ln 2)/k.
- Los sistemas que exhiben decaimiento exponencial siguen un modelo de la formay=y_0e^{−kt}.
- Los sistemas que exhiben decaimiento exponencial tienen una vida media constante, que viene dada por(\ln 2)/k.
Glosario
- tiempo de duplicación
- si una cantidad crece exponencialmente, el tiempo de duplicación es la cantidad de tiempo que tarda la cantidad en duplicarse, y viene dada por(\ln 2)/k
- decaimiento exponencial
- sistemas que exhiben decaimiento exponencial siguen un modelo de la formay=y_0e^{−kt}
- crecimiento exponencial
- sistemas que exhiben crecimiento exponencial siguen un modelo de la formay=y_0e^{kt}
- vida media
- si una cantidad decae exponencialmente, la vida media es la cantidad de tiempo que tarda la cantidad en reducirse a la mitad. Está dado por(\ln 2)/k


