Saltar al contenido principal
LibreTexts Español

8.2: Dividiendo por (x - c)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    117725

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Ahora restringimos nuestra atención al caso donde el divisor es\(g(x)=x-c\) para algún número real\(c\). En este caso, el resto\(r\) de la división\(f(x)\) por\(g(x)\) es un número real. Hacemos las siguientes observaciones.

    Observación: Resto

    Supongamos que\(g(x)=x-c\), y la larga división de\(f(x)\) por\(g(x)\) tiene resto\(r\), es decir,

    \[\text{Assumption: } f(x)=q(x)\cdot (x-c)+r \nonumber \]

    Cuando evaluamos ambos lados en la ecuación anterior en\(x=c\) vemos eso\(f(c)=q(c)\cdot (c-c)+r = q(c)\cdot 0 + r=r\). En resumen:

    \[\boxed{\text{The remainder when dividing $f(x)$ by $(x-c)$ is } \quad r=f(c)}\]

    En particular:

    \[\boxed{f(c)=0 \quad \iff \quad g(x)=x-c \text{ is a factor of } f(x)}\]

    La declaración anterior\(\PageIndex{1}\) se llama teorema del resto, y\(\PageIndex{2}\) se llama teorema del factor.

    El teorema del resto

    El resto al dividir\(f(x)\) por\((x-c)\) es\(r=f(c)\)

    El teorema de los factores

    \(f(c)=0 \quad \iff \quad g(x)=x-c\)es un factor de\(f(x)\)

    Ejemplo\(\PageIndex{1}\)

    Encuentra el resto de dividir\(f(x)=x^2+3x+2\) por

    1. \(x-3\)
    2. \(x+4\)
    3. \(x+1\)
    4. \(x-\dfrac{1}{2}\)

    Solución

    Por Observación, sabemos que el resto\(r\) de la división por\(x-c\) es\(f(c)\).

    1. Así, el resto de la parte (a), al dividir por\(x-3\) es\[r=f(3)=3^2+3\cdot 3+2=9+9+2=20 \nonumber \]
    2. Para (b), tenga en cuenta que\(g(x)=x+4=x-(-4)\), para que tomemos\(c=-4\) por nuestro insumo dando eso\(r= f(-4)=(-4)^2+3\cdot (-4)+2=16-12+2=6\).

    Del mismo modo, los demás restos son:

    1. \(r=f(-1)=(-1)^{2}+3 \cdot(-1)+2=1-3+2=0\)
    2. \(r=f\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^{2}+\dfrac{1}{2} \cdot 3+2=\dfrac{1}{4}+\dfrac{3}{2}+2=\dfrac{1+6+8}{4}=\dfrac{15}{4}\)

    Tenga en cuenta que en la parte (c), encontramos un resto\(0\), por lo que\((x+1)\) es un factor de\(f(x)\).

    Ejemplo\(\PageIndex{2}\)

    Determinar si\(g(x)\) es un factor de\(f(x)\).

    1. \(f(x)=x^3+2x^2+5x+1, \quad g(x)=x-2\)
    2. \(f(x)=x^4+4 x^3+x^2+18, \quad g(x)=x+3\)
    3. \(f(x)=x^5+3x^2+7, \quad g(x)=x+1\)

    Solución

    1. Tenemos que determinar si\(2\) es una raíz de\(f(x)=x^3+2x^2+5x+1\), es decir, si\(f(2)\) es cero. \[f(2)=2^3+2\cdot 2^2+5\cdot 2+1=8+8+10+1=27 \nonumber \]Ya que\(f(2)=27\neq 0\), vemos que no\(g(x)=x-2\) es un factor de\(f(x)\).
    2. Ahora,\(g(x)=x+3=x-(-3)\), para que calculemos:\[f(-3)=(-3)^4+4\cdot (-3)^3+(-3)^2-18=81-108+9+18=0 \nonumber \] Dado que el resto es cero, vemos que\(x+3\) es un factor de\(x^4+4\cdot x^3+x^2+18\). Por lo tanto, si quisiéramos encontrar el otro factor, podríamos usar la división larga para obtener el cociente.
    3. Por último, tenemos: no\[f(-1)=(-1)^5+3\cdot (-1)^2+7=-1+3+7=9 \nonumber \]\(g(x)=x+1\) es un factor de\(f(x)=x^5+3x^2+7\).

    Ejemplo\(\PageIndex{3}\)

    1. Demuestre que\(-2\) es una raíz de\(f(x)=x^5-3\cdot x^3+5x^2-12\), y use esto para factorizar\(f\).
    2. Demuestre que\(5\) es una raíz de\(f(x)=x^3-19x-30\), y use esto para factorizar\(f\) completamente.

    Solución

    1. Primero, calculamos que\(-2\) es una raíz. \[f(-2)=(-2)^5-3\cdot (-2)^3+5\cdot (-2)^2+12=-32+24+20-12=0 \nonumber \]Así podemos dividirnos\(f(x)\) por\(g(x)=x-(-2)=x+2\):

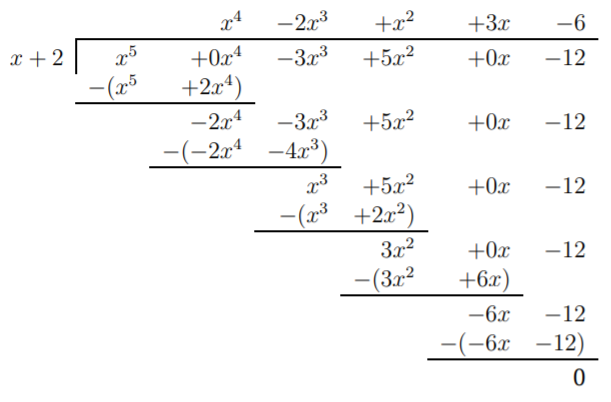
    clipboard_e1c96939e2d6d3abceeeecb8915d07745.png

    Así que factorizamos\(f(x)\) como\(f(x)=(x^4-2x^3+x^2+3x-6)\cdot (x+2)\).

    1. Nuevamente empezamos calculando\(f(5)\): División\[f(5)=5^3-19\cdot 5-30=125-95-30=0 \nonumber \] larga por\(g(x)=x-5\) da:

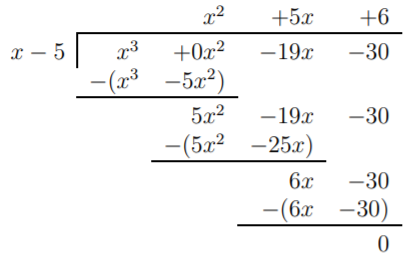
    clipboard_e4af6d5b16f19149e4220421e866c42ac.png

    Por lo tanto,\(x^3-19x-30=(x^2+5x+6)\cdot(x-5)\). Para factorizar\(f\) completamente, también factorizamos\(x^2+5x+6\). \[f(x)=(x^2+5x+6)\cdot(x-5)=(x+2)\cdot(x+3)\cdot(x-5) \nonumber \]

    This page titled 8.2: Dividiendo por (x - c) is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Thomas Tradler and Holly Carley (New York City College of Technology at CUNY Academic Works) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.