8.3: Sección opcional- División sintética

Última actualización
Guardar como PDF

Page ID: 117730

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Al dividir un polinomio$f(x)$ por$g(x)=x-c$, el cálculo real de la división larga tiene muchas repeticiones innecesarias, y es posible que queramos reducir esta redundancia tanto como sea posible. De hecho, podemos extraer la parte esencial de la división larga, cuyo resultado se llama división sintética.

Ejemplo$\PageIndex{1}$

Nuestro primer ejemplo es la larga división de$\dfrac{5x^3+7x^2+x+4}{x+2}$.

Solución

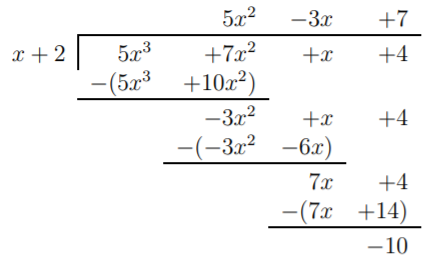
$clipboard_e0429e2e38938c4948dc456cb9813bfd6.png$

Aquí, el primer término$5x^2$ del cociente se acaba de copiar del primer término del dividendo. Esto lo registramos junto con los coeficientes del dividendo$5x^3+7x^2+x+4$ y del divisor de la$x+2=x-(-2)$ siguiente manera:

\ [\ begin {array} {c|cccc} & 5 & 7 & 1 & 4\ qquad\ text {(dividendo)} (5 x^ {3} +7 x^ {2} +x+4)\\
-2 &&&&\ text {(divisor)} (x- (-2))\
\ hline\\
& 5 &&&\ text {(cociente)}\
\ end {array}\ nonumber\]

El primer cálculo real se realiza al multiplicar el$5x^2$ término por$2$, y restarlo de$7x^2$. Esto lo registramos de la siguiente manera.

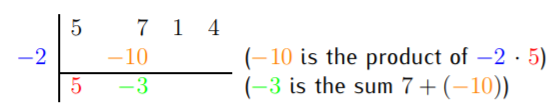
$clipboard_e12d78d348a9a2200177b7d7762e872ee.png$

De igual manera, obtenemos el siguiente paso multiplicando el$2x$ por$(-3)$ y restándolo de$1x$. Por lo tanto, obtenemos:

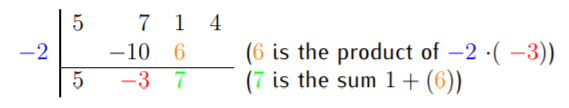
$clipboard_eab5c90d60c6540c61329459e499468af.png$

El último paso multiplica$7$ tiempos$2$ y resta esto de$4$. En definitiva, escribimos:

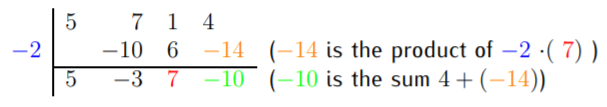
$clipboard_ee43fd018237b1db279ed1fa299792eed.png$

La respuesta se puede determinar a partir de estos coeficientes. El cociente es$5x^2-3x+7$, y el resto lo es$-10$.

Ejemplo$\PageIndex{2}$

Encuentra los siguientes cocientes vía división sintética.

$\dfrac{4x^3-7x^2+4x-8}{x-4}$
$\dfrac{x^4-x^2+5}{x+3}$

Solución

Tenemos que realizar la división sintética. \ [\ begin {array} {c|cccc} & 4 & -7 & 4 & -8\\
4 && 16 & 36 & 160\\
\ hline\\
& 4 & 9 & 40 & 152\\
\ end {array}\ nonumber\]
Por lo tanto tenemos

\[\dfrac{4x^3-7x^2+4x-8}{x-4}=4x^2+9x+40+\dfrac{152}{x-4} \nonumber \]
De igual manera, calculamos la parte (b). Tenga en cuenta que algunos de los coeficientes son ahora cero. \ [\ begin {array} {c|ccccc} & 1 &\ quad 0 & -1 &\ quad 0 & 5\\
-3 && -3 &\ quad 9 & -24 & 72\
\ hline\\
& 1 & -3 & 8 & -24 & 77\
\ end {array}\ nonumber\]

Obtenemos el siguiente resultado:

\[\dfrac{x^4-x^2+5}{x+3}=x^3-3x^2+8x-24+\dfrac{77}{x+5} \nonumber \]

Nota

La división sintética solo funciona cuando se divide por un polinomio de la forma$x-c$. No intente utilizar este método para dividir por otras formas como$x^2+2$.

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Nota