Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

8.1: División larga

Última actualización

30 oct 2022
Guardar como PDF
- 8: Dividir polinomios
- 8.2: Dividiendo por (x - c)

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Ahora mostramos cómo dividir dos polinomios. El método es similar a la división larga de los números naturales. Nuestro primer ejemplo muestra el procedimiento con todo detalle.

Ejemplo $\PageIndex{1}$

Divida las siguientes fracciones por división larga:

$\dfrac{3571}{11}$
$\dfrac{x^3+5x^2+4x+2}{x+3}$

Solución

Recordemos el procedimiento para la división larga de números naturales:

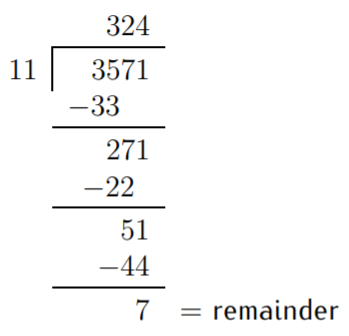
$clipboard_eeb7697e1afc4c40945de83b978221c5a.png$

Los pasos anteriores se realizan de la siguiente manera. Primero, encontramos el múltiplo más grande de $11$ menos o igual a $35$ . La respuesta $3$ se escribe como el primer dígito en la línea superior. Multiplicar $3$ tiempos $11$ y restar la respuesta $33$ de los dos primeros dígitos $35$ del dividendo. Los dígitos restantes $71$ se copian a continuación para dar $271$ . Ahora repetimos el procedimiento, hasta llegar al resto $7$ . En definitiva, lo que hemos demostrado es que:

$3571=324\cdot 11 +7\quad\text{ or alternatively, }\quad \dfrac{3571}{11}=324+\dfrac{7}{11} \nonumber$

Repetimos los pasos de la parte (a) de la siguiente manera. Primero, escribe el dividendo y divisor en el formato anterior:

A continuación, considere el plazo más alto $x^3$ del dividendo y el plazo más alto $x$ del divisor. Ya que $\dfrac{x^3}{x}=x^2$ , comenzamos con el primer término $x^2$ del cociente:

Paso 1:

\ [\ begin {array} {r}
x^2\ qquad\ quad\ phantom {)}\\
x+3 {\ overline {\ smash {\ big)}\, x ^ {3} + 5 x ^ {2} + 4 x + 2\ phantom {)}}}\
\ fantasma {)}}
\ end {array}\ nonumber\]

Multiplique $x^2$ por el divisor $x+3$ y escríbelo por debajo del dividendo:

Paso 2:

\ [\ begin {array} {r}
x^2\ qquad\ quad\ phantom {)}\\
x+3 {\ overline {\ smash {\ big)}\, x ^ {3} + 5 x ^ {2} + 4 x + 2\ phantom {)}}}\\
{x^3+3x^2\ qquad\ qquad\;}\
\ phantom {)}
\ end {array}\ nonumber\]

Ya que necesitamos restar $x^3+3x^2$ , así sumamos equivalentemente su negativo (no olvide distribuir el negativo):

Paso 3:

\ [\ begin {array} {r}
x^2\ qquad\ quad\ phantom {)}\\
x+3 {\ overline {\ smash {\ big)}\, x^3+ 5x^2+4x+2\ phantom {)}}}\\
{\ subrayado {- (x^3+3x^2)\ qquad\ qquad}\;}\\
2x^2\ qquad\ qquad\;\;\\
\ phantom {)}
\ end {array}\ nonumber\]

Ahora, lleve abajo los términos restantes del dividendo:

Paso 4:

\ [\ begin {array} {r}
x^2\ qquad\ quad\ phantom {)}\\
x+3 {\ overline {\ smash {\ big)}\, x^3+ 5x^2+4x+2\ phantom {)}}}\\
{\ subrayado {- (x^3+3x^2)\ qquad\ qquad}\;}\\
2x^2+4x+2\;\\
\ phantom {)}
\ end {array}\ nonumber\]

Ahora, repita los pasos 1-4 para el polinomio restante $2x^2+4x+2$ . El resultado después de pasar por los pasos 1-4 es el siguiente:

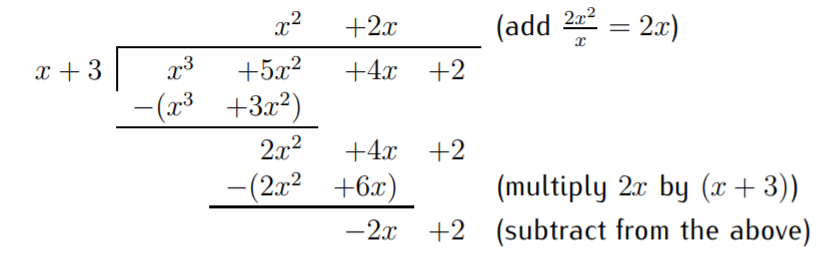
$clipboard_e0b594a879f1330ce8a859f577355b8f8.png$

Ya que se $x$ puede dividir en $-2x$ , podemos continuar con los pasos anteriores 1-4 una vez más. El resultado es el siguiente:

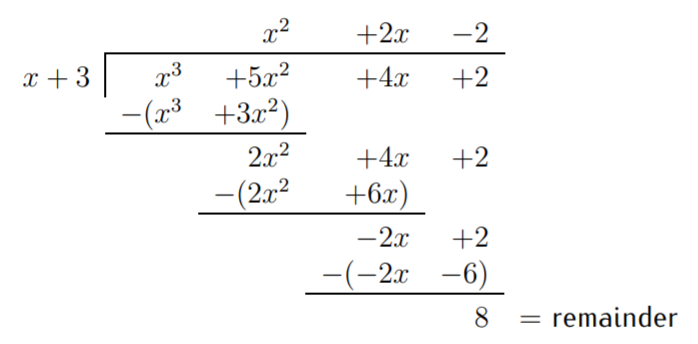
$clipboard_e8c07e409ef28fad6bd113a642c2b826b.png$

Tenga en cuenta que ahora $x$ no se puede dividir en $8$ así que nos detenemos aquí. El término final $8$ se llama el resto. Al término $x^2+2x-2$ se le llama cociente. En analogía con nuestro resultado en la parte (a), podemos escribir nuestra conclusión como:

$x^3+5x^2+4x+2=(x^2+2x-2)\cdot (x+3)+8 \nonumber$

Alternativamente, también podríamos dividir esto por $(x+3)$ y escribirlo como:

$\dfrac{x^3+5x^2+4x+2}{x+3}=x^2+2x-2+\dfrac{8}{x+3} \nonumber$

Nota

Al igual que con una operación de división que involucra números $\dfrac{f(x)}{g(x)}$ , al dividir, $f(x)$ se llama dividendo y $g(x)$ se llama divisor. Como resultado de dividir $f(x)$ por $g(x)$ vía división larga con cociente $q(x)$ y resto $r(x)$ , podemos escribir

$\dfrac{f(x)}{g(x)} = q(x)+\dfrac{r(x)}{g(x)} \nonumber$

Si multiplicamos esta ecuación por $g(x)$ , obtenemos la siguiente versión alternativa:

$f(x)=q(x)\cdot g(x)+r(x) \nonumber$

Ejemplo $\PageIndex{2}$

Divida las siguientes fracciones por división larga.

$\dfrac{x^2+4x+5}{x-4}$
$\dfrac{x^4+3x^3-5x+1}{x+1}$
$\dfrac{4x^3+2x^2+6x+18}{2x+3}$
$\dfrac{x^3+x^2+2x+1}{x^2+3x+1}$

Solución

Para la parte (a), calculamos:

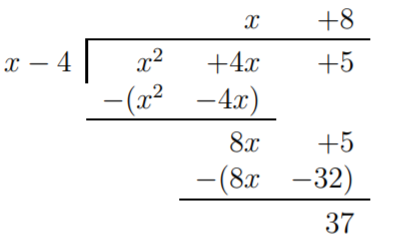
$clipboard_e7d78d13200bacd77e535af21baff3bde.png$

Por lo tanto, $x^2+4x+5=(x+8)\cdot(x-4)+37$ .

Ahora, para la parte b), no hay $x^2$ término en el dividendo. Esto se puede resolver sumando $+0\, x^2$ al dividendo:

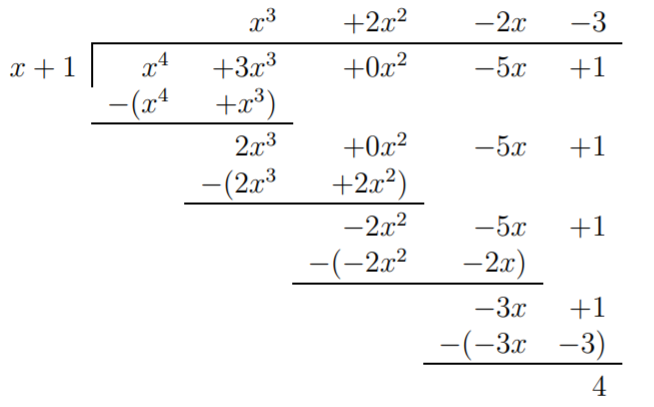
$clipboard_e9c652f243e301e871d6e01cf0626df24.png$

Por lo tanto, mostramos:

$\dfrac{x^4+3x^3-5x+1}{x+1}=x^3+2x^2-2x-3+\dfrac{4}{x+1} \nonumber$

Para (c), calcule:

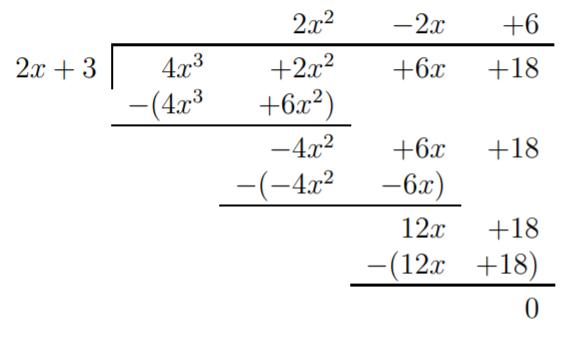
$clipboard_e91f3b39c060bd6e7b9d3490048dfd1d9.png$

Como el resto es cero, logramos factorizar $4x^3+2x^2+6x+18$ :

$4x^3+2x^2+6x+18=(2x^2-2x+6)\cdot (2x+3) \nonumber$

d) El último ejemplo tiene un divisor que es un polinomio de grado $2$ . Por lo tanto, el resto no es un número, sino un polinomio de grado $1$ .

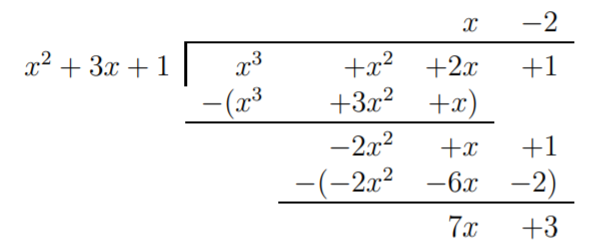
$clipboard_ed618933bb03f74546f3b31012d35898a.png$

Aquí, el resto es $r(x)=7x+3$ .

$\dfrac{x^3+x^2+2x+1}{x^2+3x+1}= x-2+\dfrac{7x+3}{x^2+3x+1} \nonumber$

Nota

El divisor $g(x)$ es un factor de $f(x)$ exactamente cuando el resto $r(x)$ es cero, es decir:

$f(x)=q(x)\cdot g(x)\quad \iff\quad r(x)=0 \nonumber$

Por ejemplo, en el Ejemplo anterior $\PageIndex{3}$ , sólo la parte (c) da como resultado una factorización del dividendo, ya que ésta es la única parte con resto cero.

Ejemplo8.1.1\PageIndex{1}

Nota

Ejemplo8.1.2\PageIndex{2}

Nota

Support Center

How can we help?

Ejemplo $\PageIndex{1}$

Ejemplo $\PageIndex{2}$