Saltar al contenido principal
LibreTexts Español

9.6: Comportamiento de los gases no ideales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    1873

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    habilidades para desarrollar

    • Describir los factores físicos que conducen a desviaciones del comportamiento ideal del gas
    • Explicar cómo se representan estos factores en la ecuación de van der Waals
    • Definir la compresibilidad (Z) y describir cómo su variación con la presión refleja un comportamiento no ideal
    • Cuantifique el comportamiento no ideal comparando los cálculos de las propiedades del gas usando la ley del gas ideal y la ecuación de van der Waals

    Hasta ahora, la ley de gas ideal, PV = nRT, se ha aplicado a una variedad de diferentes tipos de problemas, que van desde la estequiometría de reacción y los problemas de fórmulas empíricas y moleculares para determinar la densidad y la masa molar de un gas. Sin embargo, como se mencionó en los módulos anteriores de este capítulo, el comportamiento de un gas a veces no es ideal, lo que significa que las leyes observadas no describen con precisión las relaciones observadas entre su presión, volumen y temperatura. En esta sección, se consideran las razones de estas desviaciones del comportamiento ideal del gas

    Una forma de juzgar la precisión de PV = nRT es comparando el volumen real de 1 mol de gas (su volumen molar, Vm) con el volumen molar de un gas ideal a la misma temperatura y presión. Esta relación se llama el factor de compresibilidad (Z) con:

    \[\mathrm{Z=\dfrac{molar\: volume\: of\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}{molar\: volume\: of\: ideal\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}}=\left(\dfrac{PV_m}{RT}\right)_\ce{measured}\]

    Por lo tanto, el comportamiento del gas ideal se indica cuando esta relación es igual a 1, y cualquier desviación de 1 es una indicación de un comportamiento no ideal. La Figura \(\PageIndex{1}\) muestra gráficos de Z en un amplio rango de presión para varios gases comunes.

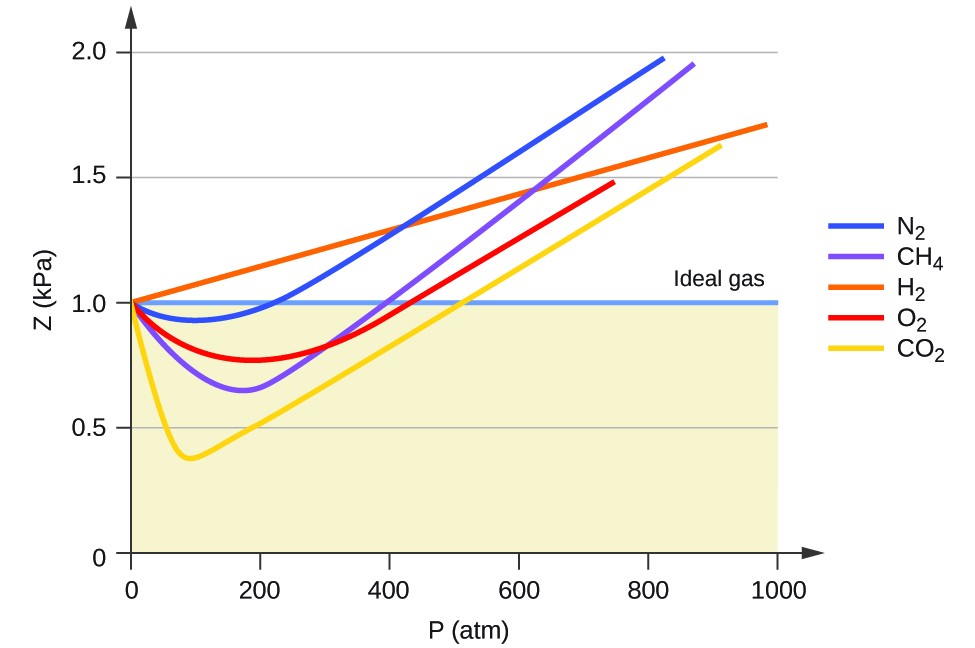
    A graph is shown. The horizontal axis is labeled, “P ( a t m ).” Its scale begins at zero with markings provided by multiples of 200 up to 1000. The vertical axis is labeled, “Z le( k P a ).” This scale begins at zero and includes multiples of 0.5 up to 2.0. Six curves are drawn of varying colors. One of these curves is a horizontal, light purple line extending right from 1.0 k P a on the vertical axis, which is labeled “Ideal gas.” The region of the graph beneath this line is shaded tan. The remaining curves also start at the same point on the vertical axis. An orange line extends to the upper right corner of the graph, reaching a value of approximately 1.7 k P a at 1000 a t m. This orange curve is labeled, “H subscript 2.” A blue curve dips below the horizontal ideal gas line initially, then increases to cross the line just past 200 a t m. This curve reaches a value of nearly 2.0 k P a at about 800 a t m. This curve is labeled, “N subscript 2.” A red curve dips below the horizontal ideal gas line initially, then increases to cross the line just past 400 a t m. This curve reaches a value of nearly 1.5 k P a at about 750 a t m. This curve is labeled, “O subscript 2.” A purple curve dips below the horizontal ideal gas line, dipping even lower than the O subscript 2 curve initially, then increases to cross the ideal gas line at about 400 a t m. This curve reaches a value of nearly 2.0 k P a at about 850 a t m. This curve is labeled, “C H subscript 4.” A yellow curve dips below the horizontal ideal gas line, dipping lower than the other curves to a minimum of about 0.4 k P a at about 0.75 a t m, then increases to cross the ideal gas line at about 500 a t m. This curve reaches a value of about 1.6 k P a at about 900 a t m. This curve is labeled, “C O subscript 2.”
    Figura \(\PageIndex{1}\): Un gráfico del factor de compresibilidad (Z) versus la presión muestra que los gases pueden exhibir desviaciones significativas del comportamiento predicho por la ley de los gases ideales.

    Como es evidente en la Figura \(\PageIndex{1}\), la ley de los gases ideales no describe bien el comportamiento de los gases a presiones relativamente altas. Para determinar por qué es esto, considere las diferencias entre las propiedades del gas real y lo que se espera de un gas ideal hipotético.

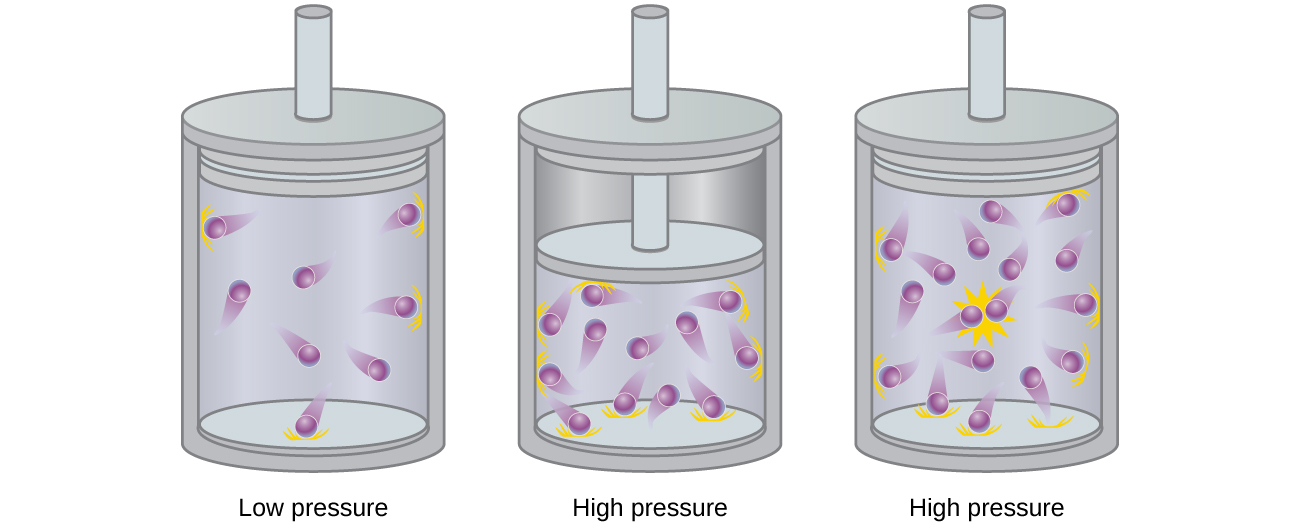
    Las partículas de un gas ideal hipotético no tienen un volumen significativo y no se atraen ni se repelen entre sí. En general, los gases reales se aproximan a este comportamiento a presiones relativamente bajas y altas temperaturas. Sin embargo, a altas presiones, las moléculas de un gas se apiñan más juntas y se reduce la cantidad de espacio vacío entre las moléculas. A estas presiones más altas, el volumen de las moléculas de gas se vuelve apreciable en relación con el volumen total ocupado por el gas (Figura \(\PageIndex{2}\)). Por lo tanto, el gas se vuelve menos compresible a estas altas presiones, y aunque su volumen continúa disminuyendo con el aumento de la presión, esta disminución no es proporcional como lo predice la ley de Boyle.

    This figure includes three diagrams. In a, a cylinder with 9 purple spheres with trails indicating motion are shown. Above the cylinder, the label, “Particles ideal gas,” is connected to two of the spheres with line segments extending into the square. The label “Assumes” is beneath the square. In b, a cylinder and piston is shown. A relatively small open space is shaded lavender with 9 purple spheres packed close together. No motion trails are present on the spheres. Above the piston, a downward arrow labeled “Pressure” is directed toward the enclosed area. In c, the cylinder is exactly the same as the first, but the number of molecules has doubled.
    Figura \(\PageIndex{2}\): Aumentar la presión de un gas aumenta la fracción de su volumen que está ocupado por las moléculas de gas y hace que el gas sea menos compresible.

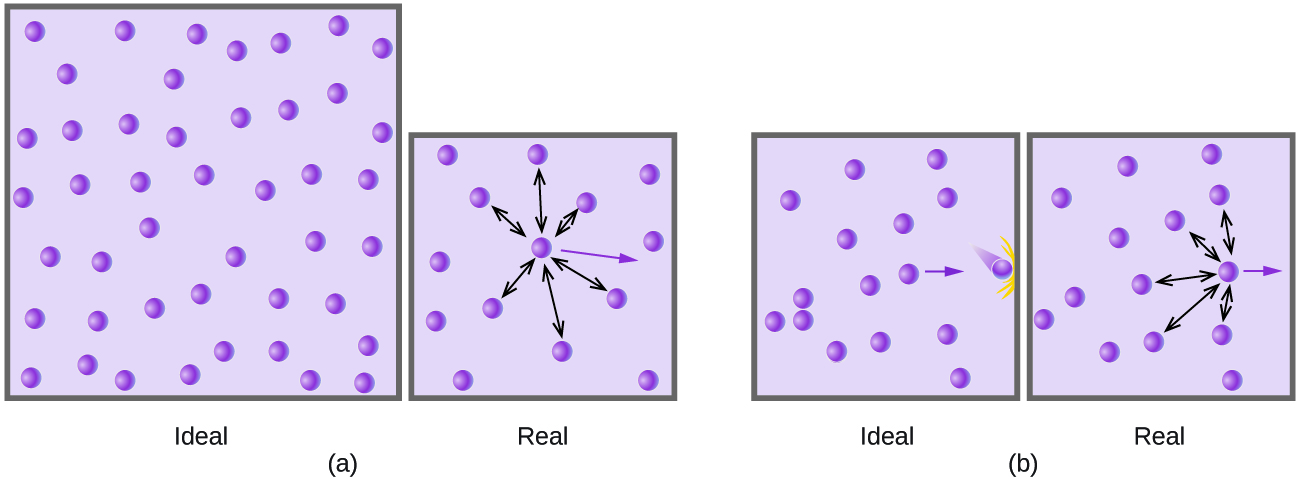
    A presiones relativamente bajas, las moléculas de gas prácticamente no se atraen entre sí porque están (en promedio) muy separadas, y se comportan casi como partículas de un gas ideal. Sin embargo, a presiones más altas, la fuerza de atracción ya no es insignificante. Esta fuerza atrae las moléculas un poco más juntas, disminuyendo un poco la presión (si el volumen es constante) o disminuyendo el volumen (a presión constante) (Figura \(\PageIndex{3}\)). Este cambio es más pronunciado a bajas temperaturas porque las moléculas tienen un KE más bajo en relación con las fuerzas de atracción, por lo que son menos efectivas para superar estas atracciones después de chocar entre sí.

    This figure includes two diagrams. Each involves two lavender shaded boxes that contain 14 relatively evenly distributed, purple spheres. In the first box in a, a nearly centrally located purple sphere has 6 double-headed arrows extending outward from it to nearby spheres. A single purple arrow is pointing right into open space. This box is labeled, “real.” There is a second box that looks slightly larger than the first box in a. It has the same number of particles but no arrows. This box is labeled, “ideal.” In b, the first box has a purple sphere at the right side which has 4 double-headed arrows radiating out to the top, bottom, and left to other spheres. A single purple arrow points right through open space to the edge of the box. This box has no spheres positioned near its right edge This box is labeled, “real.” The second box is the same size as the first box and contains the same number of particles. There are no arrows in it, except for the purple arrow which appears to be bigger and bolder. This box is labeled, “ideal.”
    Figura \(\PageIndex{3}\): (a) Las atracciones entre las moléculas de gas sirven para disminuir el volumen de gas a presión constante en comparación con un gas ideal cuyas moléculas no experimentan fuerzas atractivas. (b) Estas fuerzas atractivas disminuirán la fuerza de las colisiones entre las moléculas y las paredes del recipiente, reduciendo así la presión ejercida en comparación con un gas ideal.

    Existen varias ecuaciones diferentes que se aproximan mejor al comportamiento del gas que la ley de los gases ideales. El primero, y el más simple, fue desarrollado por el científico holandés Johannes van der Waals en 1879. La ecuación de van der Waals mejora la ley del gas ideal al agregar dos términos: uno para dar cuenta del volumen de las moléculas de gas y el otro para las fuerzas atractivas entre ellos.

    This figure shows the equation P V equals n R T, with the P in blue text and the V in red text. This equation is followed by a right pointing arrow. Following this arrow, to the right in blue text appears the equation ( P minus a n superscript 2 divided by V squared ),” which is followed by the red text ( V minus n b ). This is followed in black text with equals n R T. Beneath the second equation appears the label, “Correction for molecular attraction” which is connected with a line segment to V squared. A second label, “Correction for volume of molecules,” is similarly connected to n b which appears in red.

    El constante a corresponde a la fuerza de la atracción entre las moléculas de un gas particular, y el constante b corresponde al tamaño de las moléculas de un gas particular. La "corrección" del término de presión en la ley del gas ideal es \(\dfrac{n^2a}{V^2}\), y la "corrección" del volumen es nb. Tenga en cuenta que cuando V es relativamente grande y n es relativamente pequeño, ambos términos de corrección se vuelven insignificantes, y la ecuación de van der Waals se reduce a la ley de los gases ideales, PV = nRT. Esta condición corresponde a un gas en el que un número relativamente bajo de moléculas está ocupando un volumen relativamente grande, es decir, un gas a una presión relativamente baja. Los valores experimentales para las constantes de van der Waals de algunos gases comunes se dan en Tabla \(\PageIndex{1}\).

    Tabla \(\PageIndex{1}\): Valores de los constantes de van der Waals para algunos gases comunes
    Gas a (L2 atm/mol2) b (L/mol)
    N2 1.39 0.0391
    O2 1.36 0.0318
    CO2 3.59 0.0427
    H2O 5.46 0.0305
    He 0.0342 0.0237
    CCl4 20.4 0.1383

    A bajas presiones, la corrección de la atracción intermolecular, a, es más importante que la del volumen molecular, b. A altas presiones y pequeños volúmenes, la corrección del volumen de las moléculas se vuelve importante porque las moléculas mismas son incompresibles y constituyen una fracción apreciable del volumen total. A alguna presión intermedia, las dos correcciones tienen influencias opuestas y el gas parece seguir la relación dada por PV = nRT en un pequeño rango de presiones. Este comportamiento se refleja en las "caídas" en varias de las curvas de compresibilidad que se muestran en la Figura \(\PageIndex{1}\). La fuerza de atracción entre las moléculas inicialmente hace que el gas sea más compresible que un gas ideal, a medida que aumenta la presión (Z disminuye al aumentar P). A presiones muy altas, el gas se vuelve menos compresible (Z aumenta con P), a medida que las moléculas de gas comienzan a ocupar una fracción cada vez más significativa del volumen total de gas.

    Estrictamente hablando, la ecuación de gas ideal funciona bien cuando las atracciones intermoleculares entre las moléculas de gas son insignificantes y las moléculas de gas en sí mismas no ocupan una parte apreciable de todo el volumen. Estos criterios se cumplen en condiciones de baja presión y alta temperatura. Bajo tales condiciones, se dice que el gas se comporta de manera ideal, y las desviaciones de las leyes de gas son lo suficientemente pequeñas como para que puedan ignorarse; sin embargo, esto no es el caso siempre.

    Ejemplo \(\PageIndex{1}\): COMPARACIÓN DE LA LEY IDEAL DE GAS Y LA ECUACIÓN DE VAN DER WAALS

    Un matraz de 4.25 L contiene 3.46 moles de CO2 a 229 °C. Calcule la presión de esta muestra de CO2:

    a. de la ley de los gases ideales

    b. de la ecuación de van der Waals

    c. Explique las razones de la diferencia.

    Solución

    (a) De la ley del gas ideal:

    \(P=\dfrac{nRT}{V}=\mathrm{\dfrac{3.46\cancel{mol}×0.08206\cancel{L}atm\cancel{mol^{−1}}\cancel{K^{−1}}×502\cancel{K}}{4.25\cancel{L}}=33.5\:atm}\)

    (b) From the van der Waals equation:

    \(\left(P+\dfrac{n^2a}{V^2}\right)×(V−nb)=nRT⟶P=\dfrac{nRT}{(V−nb)}−\dfrac{n^2a}{V^2}\)

    \(P=\mathrm{\dfrac{3.46\:mol×0.08206\:L\:atm\:mol^{−1}\:K^{−1}×502\: K}{(4.25\:L−3.46\:mol×0.0427\:L\:mol^{−1})}−\dfrac{(3.46\:mol)^2×3.59\:L^2\:atm\:mol^2}{(4.25\:L)^2}}\)

    Esto finalmente produce P = 32.4 atm.

    (c) Esto no es muy diferente del valor de la ley del gas ideal porque la presión no es muy alta y la temperatura no es muy baja. El valor es algo diferente porque las moléculas de CO2 tienen cierto volumen y atracciones entre las moléculas, y la ley de los gases ideales supone que no tienen volumen ni atracciones.

    Ejercicio \(\PageIndex{1}\)

    Un matraz de 560-mL contiene 21.3 g de N2 a 145 °C. Calcule la presión de N2:

    a. de la ley de los gases ideales

    b. de la ecuación de van der Waals

    c. Explique las razones de la diferencia.

    Respuesta a

    46.562 atm

    Respuesta b

    46.594 atm

    Respuesta c

    La ecuación de van der Waals toma en cuenta el volumen de las moléculas de gas en sí mismas, así como las atracciones intermoleculares.

    Resumen

    Las moléculas de un gas poseen un volumen finito y experimentan fuerzas de atracción entre sí. En consecuencia, el comportamiento del gas no se describe muy bien por la ley del gas ideal. En condiciones de baja presión y alta temperatura, estos factores son insignificantes, la ecuación del gas ideal es una descripción precisa del comportamiento del gas, y se dice que el gas exhibe un comportamiento ideal. Sin embargo, a temperaturas más bajas y presiones más altas, se requieren correcciones para el volumen molecular y las atracciones moleculares para tener en cuenta el tamaño molecular finito y las fuerzas atractivas. La ecuación de van der Waals es una versión modificada de la ley de los gases ideales que se puede usar para dar cuenta del comportamiento no ideal de los gases en estas condiciones.

    Ecuaciones Clave

    • \(\mathrm{Z=\dfrac{molar\:volume\: of\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}{molar\: volume\: of\: ideal\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}}=\left(\dfrac{P×V_m}{R×T}\right)_\ce{measured}\)
    • \(\left(P+\dfrac{n^2a}{V^2}\right)×(V−nb)=nRT\)

    Glosario

    factor de compresibilidad (Z)
    relación del volumen molar medido experimentalmente para un gas a su volumen molar calculado a partir de la ecuación de gas ideal
    ecuación de van der Waals
    versión modificada de la ecuación del gas ideal que contiene términos adicionales para tener en cuenta el comportamiento del gas no ideal

    Contribuyentes

    This page titled 9.6: Comportamiento de los gases no ideales is shared under a CC BY license and was authored, remixed, and/or curated by OpenStax.