12.5: Las leyes de velocidad integradas

3habilidades para desarollar

• Explicar la forma y función de una ley de tasa integrada.
• Realizar cálculos de ley de tasa integrada para reacciones de cero, primer y segundo orden
• Definir la vida media y realizar cálculos relacionados.
• Identificar el orden de una reacción a partir de los datos de concentración / tiempo.

Las leyes de velocidad que hemos visto hasta ahora relacionan la velocidad y las concentraciones de los reactivos. También podemos determinar una segunda forma de cada ley de velocidad que relacione las concentraciones de los reactivos y el tiempo. Estas se llaman las leyes de tasas integradas. Podemos usar una ley de velocidad integrada para determinar la cantidad de reactivo o producto presente después de un período de tiempo o para estimar el tiempo requerido para que una reacción proceda en cierta medida. Por ejemplo, se usa una ley de velocidad integrada para determinar el período de tiempo que un material radiactivo se debe almacenar para que su radiactividad decaiga a un nivel seguro.

Usando el cálculo, la ley de velocidad diferencial para una reacción química se puede integrar con respecto al tiempo para dar una ecuación que relacione la cantidad de reactivo o producto presente en una mezcla de reacción con el tiempo transcurrido de la reacción. Este proceso puede ser muy sencillo o complejo, dependiendo de la complejidad de la ley de tasa diferencial. Para nuestros propósitos, nos centraremos en las leyes de tasa integrada resultantes para las reacciones de primer, segundo y orden cero.

Reacciones de primer orden

Una ecuación que relaciona el constante de velocidad k con la concentración inicial [A]₀ y la concentración [A]_t presente después de un tiempo dado t puede derivarse para una reacción de primer orden y demostrarse que es:

\[\ln\left(\dfrac{[A]_t}{[A]_0}\right)=−kt\]

o

\[\ln\left(\dfrac{[A]_0}{[A]_t}\right)=kt\]

o

\[[A]=[A]_0e^{−kt}\]

Ejemplo \(\PageIndex{1}\): LA LEY INTEGRADA DE velocidad PARA UNA REACCIÓN DE PRIMER ORDEN

El constante de velocidad para la descomposición de primer orden del ciclobutano, C₄H₈ a 500 °C es 9.2 × 10⁻³ s⁻¹:

\[\ce{C4H8⟶2C2H4}\]

¿Cuánto tiempo tomará en descomponerse el 80.0% de una muestra de C₄H₈?

Solución

Usamos la forma integrada de la ley de velocidad para responder preguntas sobre el tiempo:

\[\ln\left(\dfrac{[A]_0}{[A]}\right)=kt\]

Hay cuatro variables en la ley de tasas y sabemos tres de ellas, podemos determinar la cuarta. En este caso, sabemos [A]₀, [A] y k, y necesitamos encontrar t.

No se proporciona la concentración inicial de C₄H₈, [A]₀,, pero la provisión de que el 80.0% de la muestra se ha descompuesto es suficiente información para resolver este problema. Deje que x represente la concentración inicial, en cuyo caso la concentración después de una descomposición del 80.0% es 20.0% de x o 0.200x. Reorganizando la ley de velocidad para aislar t y sustituyendo los rendimientos de cantidades proporcionadas nos da:

\(\begin{align*}
t&=\ln\dfrac{[x]}{[0.200x]}×\dfrac{1}{k}\\
&=\mathrm{\ln\dfrac{0.100\:mol\: L^{−1}}{0.020\:mol\: L^{−1}}×\dfrac{1}{9.2×10^{−3}\:s^{−1}}}\\
&=\mathrm{1.609×\dfrac{1}{9.2×10^{−3}\:s^{−1}}}\\
&=\mathrm{1.7×10^2\:s}
\end{align*}\)

Ejercicio \(\PageIndex{1}\)

El yodo-131 es un isótopo radiactivo que se usa para diagnosticar y tratar algunas formas de cáncer de tiroides. El yodo-131 se descompone en xenón-131 de acuerdo con la siguiente ecuación:

\[\textrm{I-131 ⟶ Xe-131 + electron}\]

La desintegración es de primer orden con un constante de velocidad de 0.138 d⁻¹. Toda la desintegración radiactiva es de primer orden. ¿Cuántos días le tomará al 90% del yodo-131 en una solución de 0.500 M de esta sustancia para descomponerse a Xe-131?

Respuesta

16.7 dias

Podemos usar las leyes de velocidad integradas con datos experimentales que consisten en información de tiempo y concentración para determinar el orden y la velocidad constante de una reacción. La ley de velocidad integrada se puede reorganizar a un formato estándar de ecuación lineal:

\[\begin{align*}
\ln[A]&=(−k)(t)+\ln[A]_0\\
y&=mx+b
\end{align*}\]

Una gráfica de ln[A] versus t para una reacción de primer orden es una línea recta con una pendiente de −k y una intersección de ln[A]_0. Si un conjunto de datos de velocidad se traza de esta manera, pero no da como resultado una línea recta, la reacción no es de primer orden en A.

Ejemplo \(\PageIndex{2}\): Determinación del orden de la reacción usando un gráfico

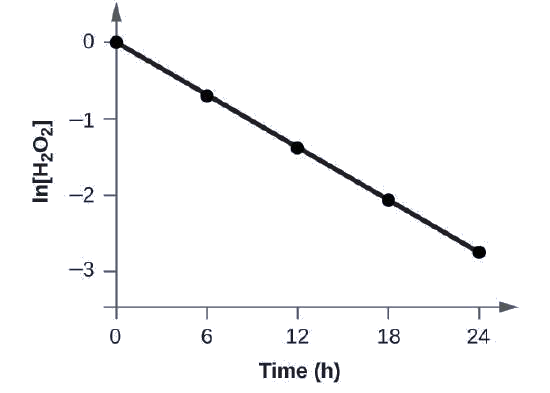
Muestre que los datos en esta Figura se pueden representar usando una ley de tasa de primer orden graficando ln[H₂O₂] versus tiempo. Determine el constante de velocidad para la descomposición del H₂O₂ a partir de estos datos.

Solución

Los datos de esta figure esta Figura con la adición de valores de ln[H₂O₂] se dan en la Figura \(\PageIndex{1}\).

Figura \(\PageIndex{1}\): La relación lineal entre el ln[H₂O₂] y el tiempo muestra que la descomposición del peróxido de hidrógeno es una reacción de primer orden.

Prueba	Tiempo (h)	[H2O2] (M)	ln[H2O2]
1	0	1.000	0.0
2	6.00	0.500	−0.693
3	12.00	0.250	−1.386
4	18.00	0.125	−2.079
5	24.00	0.0625	−2.772

La gráfica de ln[H₂O₂] versus tiempo es lineal, por lo tanto, hemos verificado que la reacción se puede describir mediante una ley de velocidad de primer orden.

El constante de velocidad para una reacción de primer orden es igual al negativo de la pendiente de la gráfica de ln[H₂O₂] versus el tiempo donde:

\[\ce{slope}=\dfrac{\textrm{change in }y}{\textrm{change in }x}=\dfrac{Δy}{Δx}=\dfrac{Δ\ln[\ce{H2O2}]}{Δt}\]

Para determinar la pendiente de la línea, necesitamos dos valores de ln[H₂O₂] a diferentes valores de t (es preferible uno cerca de cada extremo de la línea). Por ejemplo, el valor de ln[H₂O₂] cuando t es 6.00 h es −0.693; el valor cuando t = 12.00 h es −1.386:

\[\begin{align*}
\ce{slope}&=\mathrm{\dfrac{−1.386−(−0.693)}{12.00\: h−6.00\: h}}\\
&=\mathrm{\dfrac{−0.693}{6.00\: h}}\\
&=\mathrm{−1.155×10^{−2}\:h^{−1}}\\
k&=\mathrm{−slope=−(−1.155×10^{−1}\:h^{−1})=1.155×10^{−1}\:h^{−1}}
\end{align*}\]

Ejercicio \(\PageIndex{2}\)

Grafica los siguientes datos para determinar si la reacción \(A⟶B + C \) es de primer orden.

Prueba	Tiempo (s)	[A]
1	4.0	0.220
2	8.0	0.144
3	12.0	0.110
4	16.0	0.088
5	20.0	0.074

Respuesta

La gráfica de ln[A] vs. t no es una línea recta. La ecuación no es de primer orden:

Reacciones de segundo orden

Las ecuaciones que relacionan las concentraciones de reactivos y el constante de velocidad de las reacciones de segundo orden son bastante complicadas. Nos limitaremos a las reacciones de segundo orden más simples, especificamente, aquellas con tasas que dependen de la concentración de un solo reactivo y descritas por la ley de tasa diferencial:

\[\ce{Rate}=k[A]^2\]

Para estas reacciones de segundo orden, la ley de tasa integrada es:

\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\]

donde los términos en la ecuación tienen sus significados habituales como se definió anteriormente.

Ejemplo \(\PageIndex{3}\): LA LEY INTEGRADA DE TARIFAS PARA UNA REACCIÓN DE SEGUNDO ORDEN

La reacción del gas butadieno (C₄H₆) consigo mismo produce gas C₈H₁₂ en la siguiente manera:

\[\ce{2C4H6}(g)⟶\ce{C8H12}(g)\]

La reacción es de segundo orden con una velocidad constante igual a 5.76 × 10⁻² L / mol / min bajo ciertas condiciones. Si la concentración inicial del butadieno es de 0.200 M, ¿Cuál es la concentración restante después de 10.0 min?

Solución

Usamos la forma integrada de la ley de tarifas para responder preguntas sobre el tiempo. Para una reacción de segundo orden, tenemos:

\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\]

Sabemos tres variables en esta ecuación: [A]₀ = 0.200 mol / L, k = 5.76 × 10⁻² L/mol/min, y t = 10.0 min. Por lo tanto, podemos resolver para [A], la cuarta variable:

\[\begin{align*}
\dfrac{1}{[A]}&=\mathrm{(5.76×10^{−2}\:L\: mol^{−1}\:min^{−1})(10\:min)+\dfrac{1}{0.200\:mol^{−1}}}\\
\dfrac{1}{[A]}&=\mathrm{(5.76×10^{−1}\:L\: mol^{−1})+5.00\:L\: mol^{−1}}\\
\dfrac{1}{[A]}&=\mathrm{5.58\:L\: mol^{−1}}\\
[A]&=\mathrm{1.79×10^{−1}\:mol\: L^{−1}}
\end{align*}\]

Por lo tanto, quedan 0.179 mol/L de butadieno al final de 10.0 min, en comparación con los 0.200 mol /L que estaban originalmente presentes.

Ejercicio \(\PageIndex{3}\)

Si la concentración inicial de butadieno es 0.0200 M, ¿Cuál es la concentración restante después de 20.0 min?

Respuesta

0.0196 mol/L

La ley de velocidad integrada para nuestras reacciones de segundo orden tiene la forma de la ecuación de una línea recta:

\[\begin{align*}
\dfrac{1}{[A]}&=kt+\dfrac{1}{[A]_0}\\
y&=mx+b
\end{align*}\]

Un gráfica de \(\dfrac{1}{[A]}\) versus t para una reacción de segundo orden es una línea recta con una pendiente de k y una intersección de \(\dfrac{1}{[A] _0 }\). Si la trama no es una línea recta, entonces la reacción no es de segundo orden.

Ejemplo \(\PageIndex{4}\): DETERMINACIÓN DEL ORDEN DE LA REACCIÓN USANDO LOS GRÁFICOS

Pruebe los datos dados para mostrar si la dimerización de C₄H₆ es una reacción de primer o segundo orden.

Solución

Prueba	Tiempo (s)	[C4H6] (M)
1	0	1.00 × 10^−2
2	1600	5.04 × 10^−3
3	3200	3.37 × 10^−3
4	4800	2.53 × 10^−3
5	6200	2.08 × 10^−3

Para distinguir una reacción de primer orden de una reacción de segundo orden, graficamos ln[C4H6] versus t y lo comparamos con una gráfica de \(\mathrm{\dfrac{1}{[C_4H_6]}}\) versus t. Los valores necesarios para estas parcelas siguen.

Tiempo (s)	\(\dfrac{1}{[\ce{C4H6}]}\:(M^{−1})\)	ln[C4H6]
0	100	−4.605
1600	198	−5.289
3200	296	−5.692
4800	395	−5.978
6200	481	−6.175

Los gráficos se muestran en la Figura \(\PageIndex{2}\). Como puede ver, la gráfica de ln[C₄H₆] versus t no es lineal, por lo tanto, la reacción no es de primer orden. La gráfica de \(\dfrac {1}{[\ce{C4H6}]} \) versus t es lineal, lo que indica que la reacción es de segundo orden.

Figura \(\PageIndex{2}\): Estos dos gráficos muestran gráficos de primer y segundo orden para la dimerización de C₄H₆. Como el gráfico de primer orden (izquierda) no es lineal, sabemos que la reacción no es de primer orden. La tendencia lineal en el gráfico de segundo orden (derecha) indica que la reacción sigue una cinética de segundo orden.

Ejercicio \(\PageIndex{4}\)

¿Los siguientes datos se ajustan a una ley de tasa de segundo orden?

Prueba	Tiempo (s)	[A] (M)
1	5	0.952
2	10	0.625
3	15	0.465
4	20	0.370
5	25	0.308
6	35	0.230

Respuesta:

Si. La gráfica de \(\dfrac{1}{[A]}\) vs. t es lineal:

Reacciones de orden cero

Para las reacciones de orden cero, la ley de tasa diferencial es:

\[\ce{Rate}=k[A]^0=k\]

Por lo tanto, una reacción de orden cero exhibe una velocidad de reacción constante, independientemente de la concentración de sus reactivos

La ley de velocidad integrada para una reacción de orden cero también tiene la forma de la ecuación de una línea recta:

\(\begin{align*}
[A]&=−kt+[A]_0\\
y&=mx+b
\end{align*}\)

Una gráfica de [A] versus t para una reacción de orden cero es una línea recta con una pendiente de −k y una intersección de [A]₀. La Figura \(\PageIndex{3}\) muestra una gráfica de [NH₃] versus t para la descomposición del amoníaco en un alambre de tungsteno caliente y para la descomposición del amoníaco en cuarzo caliente (SiO₂). La descomposición de NH₃ en tungsteno caliente es de orden cero; la trama es una línea recta. La descomposición de NH₃ en el cuarzo caliente no es de orden cero (es de primer orden). A partir de la pendiente de la línea para la descomposición de orden cero, podemos determinar el constante de la velocidad:

\[\ce{slope}=−k=\mathrm{1.3110^{−6}\:mol/L/s}\]

Figura \(\PageIndex{3}\): La descomposición de NH₃ en una superficie de tungsteno (W) es una reacción de orden cero, mientras que en una superficie de cuarzo (SiO₂), la reacción es de primer orden.

La vida media de una reacción

La vida media de una reacción (t_1/2) es el tiempo requerido para consumir la mitad de una cantidad dada de reactivo. En cada semivida subsiguiente, se consume la mitad de la concentración restante del reactivo. Usando la descomposición del peróxido de hidrógeno como un ejemplo, encontramos que durante la primera vida media (de 0.00 horas a 6.00 horas), la concentración de H₂O₂ disminuye de 1.000 M a 0.500 M. Durante la segunda vida media (de 6.00 horas a 12.00 horas), la concentración de H₂O₂ disminuye de 0.500 M a 0.250 M; durante la tercera vida media, disminuye de 0.250 M a 0.125 M. La concentración de H₂O₂ disminuye por la mitad durante cada período sucesivo de 6.00 horas. La descomposición del peróxido de hidrógeno es una reacción de primer orden y, como se puede mostrar, la vida media de una reacción de primer orden es independiente de la concentración del reactivo. Sin embargo, las vidas medias de las reacciones con otros órdenes dependen de las concentraciones de los reactivos.

Reacciones de primer orden

Podemos derivar una ecuación para determinar la vida media de una reacción de primer orden a partir de la forma alternativa de la ley de velocidad integrada de la siguiente manera:

\[\begin{align*}
\ln\dfrac{[A]_0}{[A]}&=kt\\
t&=\ln\dfrac{[A]_0}{[A]}×\dfrac{1}{k}
\end{align*}\]

Si establecemos el tiempo t que sea igual a la vida media, \(t_{1/2}\), la concentración correspondiente de A en este momento es igual a la mitad de su concentración inicial. Por lo tanto, cuando \(t=t_{1/2}\), \([A]=\dfrac{1}{2}[A]_0\).

Por lo tanto:

\[\begin{align*}
t_{1/2}&=\ln\dfrac{[A]_0}{\dfrac{1}{2}[A]_0}×\dfrac{1}{k}\\
&=\ln 2×\dfrac{1}{k}=0.693×\dfrac{1}{k}
\end{align*}\]

En consecuencia:

\[t_{1/2}=\dfrac{0.693}{k}\]

Podemos ver que la vida media de una reacción de primer orden es inversamente proporcional al constante de velocidad k. Una reacción rápida (vida media más corta) tendrá una valor de k más grande; una reacción lenta (vida media más larga) tendrá una valor de k más bajo.

Ejemplo \(\PageIndex{5}\): CÁLCULO DE UN CONSTANTE DE TASA DE PRIMER ORDEN USANDO LA MEDIA VIDA

Calculate the rate constant for the first-order decomposition of hydrogen peroxide in water at 40 °C, using the data given in Figure \(\PageIndex{4}\).

Figura \(\PageIndex{4}\): Se ilustra la descomposición del H₂O₂ \(\ce{(2H2O2⟶2H2O+O2)}\) a 40 °C. La intensidad del color simboliza la concentración de H₂O₂ en los tiempos indicados; H2O2 es en realidad incoloro.

Solución

La vida media para la descomposición del H₂O₂ es 2.16 × 10⁴ s:

\[\begin{align*}
t_{1/2}&=\dfrac{0.693}{k}\\
k&=\dfrac{0.693}{t_{1/2}}=\dfrac{0.693}{2.16×10^4\:\ce s}=3.21×10^{−5}\:\ce s^{−1}
\end{align*}\]

Ejercicio \(\PageIndex{1}\)

La descomposición radiactiva de primer orden del yodo-131 exhibe un constante de velocidad de 0.138 d⁻¹. ¿Cuál es la vida media de esta descomposición?

Respuesta

5.02 d.

Reacciones de segundo orden

Podemos derivar la ecuación para calcular la vida media de una reacción de segundo orden de la siguiente manera:

\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\]

o

\[\dfrac{1}{[A]}−\dfrac{1}{[A]_0}=kt\]

Si

\[t=t_{1/2}\]

luego

\[[A]=\dfrac{1}{2}[A]_0\]

y podemos escribir:

\(\begin{align*}
\dfrac{1}{\dfrac{1}{2}[A]_0}−\dfrac{1}{[A]_0}&=kt_{1/2}\\
2[A]_0−\dfrac{1}{[A]_0}&=kt_{1/2}\\
\dfrac{1}{[A]_0}&=kt_{1/2}
\end{align*}\)

Así:

\[t_{1/2}=\dfrac{1}{k[A]_0}\]

Para una reacción de segundo orden, \(t_{1/2}\) es inversamente proporcional a la concentración del reactivo, y la vida media aumenta a medida que avanza la reacción porque la concentración del reactivo disminuye. En consecuencia, encontramos que el uso del concepto de vida media es más complejo para las reacciones de segundo orden que para las reacciones de primer orden. A diferencia de las reacciones de primer orden, el constante de velocidad de una reacción de segundo orden no se puede calcular directamente a partir de la vida media a menos que se conozca la concentración inicial de reactivo.

Reacciones de orden cero

Podemos derivar una ecuación para calcular la vida media de una reacción de orden cero de la siguiente manera:

\[[A]=−kt+[A]_0\]

Cuando se ha consumido la mitad de la cantidad inicial del reactivo \(t=t_{1/2}\) and \([A]=\dfrac{[A]_0}{2}\). En consecuencia:

\[\begin{align*}
\dfrac{[A]_0}{2}&=−kt_{1/2}+[A]_0\\
kt_{1/2}&=\dfrac{[A]_0}{2}
\end{align*}\]

y

\[t_{1/2}=\dfrac{[A]_0}{2k}\]

La vida media de una reacción de orden cero aumenta a medida que aumenta la concentración inicial de reactivo. Las ecuaciones para las leyes de tasa diferencial e integrada y las semividas correspondientes para las reacciones de cero, y también de primer y segundo orden se resumen en la Tabla \(\PageIndex{1}\).

Tabla \(\PageIndex{1}\): Summary of Rate Laws for Zero-, First-, and Second-Order Reactions

	Orden cero	Primer orden	Segundo orden
ley de tasas	tasa = k	tasa = k[A]	tasa = k[A]^2
unidades de tasa constante	M s^−1	s^−1	M^−1 s^−1
ley de tasa integrada	[A] = −kt + [A]0	ln[A] = −kt + ln[A]0	\(\dfrac{1}{[A]}=kt+\left(\dfrac{1}{[A]_0}\right)\)
gráfico necesario para ajustar lineal de datos de velocidad	[A] vs. t	ln[A] vs. t	\(\dfrac{1}{[A]}\) vs. t
relación entre la pendiente del gráfico lineal y la tasa constante	k = −slope	k = −slope	k = +slope
media-vida	\(t_{1/2}=\dfrac{[A]_0}{2k}\)	\(t_{1/2}=\dfrac{0.693}{k}\)	\(t_{1/2}=\dfrac{1}{[A]_0k}\)

Resumen

Las leyes de tasas diferenciales se pueden determinar por el método de tasas iniciales u otros métodos. Medimos valores para las velocidades iniciales de una reacción a diferentes concentraciones de reactivos. A partir de estas mediciones, determinamos el orden de la reacción en cada reactivo. Las leyes de tasa integrada se determinan mediante la integración de las leyes de tasa diferencial correspondientes. Los constantes de velocidad para esas leyes de velocidad se determinan a partir de las mediciones de la concentración en diversos momentos durante una reacción.

La vida media de una reacción es el tiempo requerido para disminuir la cantidad de un reactivo dado a la mitad. La vida media de una reacción de orden cero disminuye a medida que disminuye la concentración inicial del reactivo en la reacción. La vida media de una reacción de primer orden es independiente de la concentración, y la vida media de una reacción de segundo orden disminuye a medida que aumenta la concentración.

Ecuaciones Clave

• ley de tasa integrada para reacciones de orden cero: \([A]=−kt+[A]_0\), \(t_{1/2}=\dfrac{[A]_0}{2k}\)
• ley de tasa integrada para reacciones de primer orden: \(\ln[A]=−kt+[A]_0\), \(t_{1/2}=\dfrac{0.693}{k}\)
• ley de tasa integrada para reacciones de primer orden: \(\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\), \(t_{1/2}=\dfrac{1}{[A]_0k}\

Glosario

vida media de una reacción (t _1/2)

tiempo requerido para consumir la mitad de una cantidad dada de reactivo

ley de tasa integrada

ecuación que relaciona la concentración de un reactivo con el tiempo transcurrido de la reacción

Contribuyebtes

• Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.