12.6: Teoría de colisión
- Page ID
- 1898
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)habilidades para desarrollar
- Utilice los postulados de la teoría de colisión para explicar los efectos del estado físico, la temperatura y la concentración en las velocidades de la reacción.
- Definir los conceptos de energía de activación y estado de transición.
- Utilice la ecuación de Arrhenius en los cálculos que relacionan los constantes de velocidad con la temperatura.
No debería sorprendernos que los átomos, las moléculas o los iones deben colisionar antes de que puedan reaccionar entre sí. Los átomos deben estar juntos para formar enlaces químicos. Esta simple premisa es la base de una teoría muy poderosa que explica muchas observaciones con respecto a la cinética química, incluidos los factores que afectan las velocidades de la reacción. La teoría de colisión se basa en los siguientes postulados:
postulados de la teoría de colisión
- La velocidad de una reacción es proporcional a la velocidad de las colisiones de los reactivos: \[\mathrm{reaction\: rate ∝ \dfrac{\#\,collisions}{time}}\]
- Las especies que reaccionan deben colisionar en una orientación que permita el contacto entre los átomos que se unirán en el producto.
- La colisión debe ocurrir con la energía adecuada para permitir la penetración mutua de las capas de valencia de las especies que reaccionan para que los electrones se puedan reorganizar y formar nuevos enlaces.
Podemos ver la importancia de los dos factores físicos señalados en los postulados 2 y 3, la orientación y la energía de las colisiones, cuando consideramos la reacción del monóxido del carbono con el oxígeno:
\[\ce{2CO}(g)+\ce{O2}(g)⟶\ce{2CO2}(g)\]
El monóxido de carbono es un contaminante producido por la combustión de combustibles de los hidrocarburos. Para reducir este contaminante, los automóviles tienen convertidores catalíticos que usan un catalizador para llevar a cabo esta reacción. También es una reacción secundaria de la combustión de la pólvora que provoca el destello de la boca de muchas armas de fuego. Si el monóxido de carbono y el oxígeno están presentes en cantidad suficiente, la reacción es espontánea a alta temperatura y presión.
El primer paso en la reacción en fase gaseosa entre el monóxido de carbono y el oxígeno es una colisión entre las dos moléculas
\[\ce{CO}(g)+\ce{O2}(g)⟶\ce{CO2}(g)+\ce{O}(g)\]
El primer paso en la reacción en fase gaseosa entre el monóxido de carbono y el oxígeno es una colisión entre las dos moléculas:Aunque hay muchas diferentes orientaciones posibles que las dos moléculas pueden tener una respecto a la otra, considere las dos presentadas en la Figura \(\PageIndex{1}\). En el primer caso, el lado del oxígeno de la molécula de monóxido de carbono colisiona con la molécula del oxígeno. En el segundo caso, el lado del carbono de la molécula del monóxido de carbono colisiona con la molécula del oxígeno. Claramente, el segundo caso es más probable en resultar en la formación del dióxido de carbono, que tiene un átomo de carbono central unido a dos átomos de oxígeno \(\ce{(O=C=O)}\). Este es un ejemplo bastante simple que demuestra la importancia de la orientación de la colisión en términos de crear el producto deseado de la reacción.

Si la colisión toma lugar con la orientación correcta, todavía no hay garantía de que la reacción proceda a formar el dióxido de carbono. Cada reacción requiere una cierta cantidad de energía de activación para que avance en la dirección hacia adelante, produciendo un complejo activado apropiado en el camino. Como lo demuestra la Figura \(\PageIndex{2}\), incluso una colisión con la orientación correcta puede fallar al formar el producto de la reacción. En el estudio de los mecanismos de reacción, cada una de estas tres disposiciones de átomos se llama un complejo activado propuesto o estado de transición.
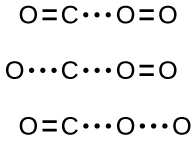
En la mayoría de las circunstancias, es imposible aislar o identificar un estado de transición o complejo activado. En la reacción entre el monóxido de carbono y el oxígeno para formar el dióxido de carbono, los complejos activados solo se han observado espectroscópicamente en sistemas que usan un catalizador heterogéneo. La reacción en fase gaseosa ocurre demasiado rápido para aislar cualquiera de estos compuestos químicos.
La teoría de colisión explica por qué la mayoría de las velocidades de reacción aumentan a medida que aumentan las concentraciones. Con un aumento en la concentración de cualquier sustancia reaccionante, las posibilidades de las colisiones entre las moléculas aumentan porque hay más moléculas por unidad de volumen. Más colisiones significan una velocidad de reacción más rápida, suponiendo que la energía de las colisiones sea adecuada.
Energía de activación y la ecuación de Arrhenius
La energía mínima necesaria para formar un producto durante una colisión entre ciertos reactivos se llama la energía de activación (\(E_a\)). La energía cinética de las moléculas reactivas juega un papel importante en una reacción porque la energía necesaria para formar un producto es proporcionada por una colisión de una molécula reactiva con otra molécula reactiva. (En las reacciones conteniendo solamente un reactivo, la energía de activación puede ser proporcionada por una colisión de la molécula de reactivo con la pared del recipiente de reacción o con moléculas de un contaminante inerte). Si la energía de activación es mucho mayor que la energía cinética promedio de las moléculas, la reacción ocurrirá lentamente: solo unas pocas moléculas de rápido movimiento tendrán suficiente energía para reaccionar. Si la energía de activación es mucho menor que la energía cinética promedio de las moléculas, la fracción de moléculas que poseen la energía cinética necesaria será grande; la mayoría de las colisiones entre moléculas causaran una reacción, y la reacción ocurrirá rápidamente.
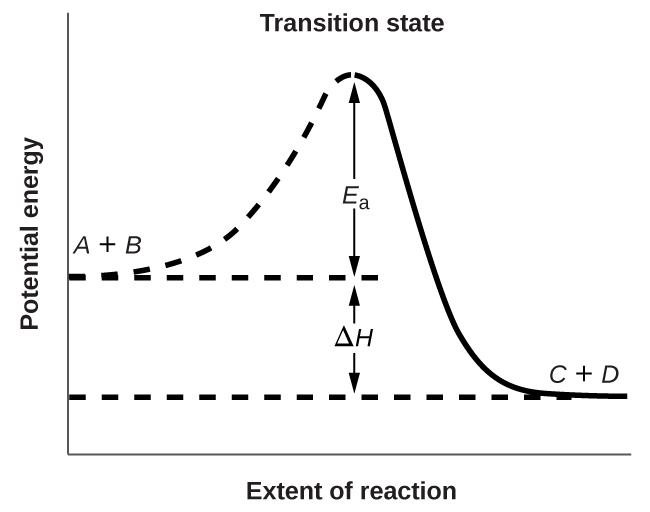
La figura \(\PageIndex{3}\) muestra las relaciones de energía para una reacción general de una molécula de \(A\) con una molécula de \(B\) para formar las moléculas de \(C\) y \(D\):
\[A+B⟶C+D\]
La figura muestra que la energía del estado de transición es más grande que la de los reactivos \(A\) y \(B\) en una cantidad igual a \(E_a\), la energía de activación. Por lo tanto, la suma de las energías cinéticas de \(A\) y \(B\) debe ser igual o mayor que Ea para alcanzar el estado de transición. Después de que se ha alcanzado el estado de transición, y cuando \(C\) y \(D\) comienzan a formarse, el sistema pierde energía hasta que su energía total es menor que la de la mezcla inicial. Esta energía perdida se transfiere a otras moléculas, dándoles suficiente energía para alcanzar el estado de transición. La reacción entre los reactivos \(A\) y \(B\)), por lo tanto, tiende a ocurrir fácilmente una vez que la reacción ha comenzado. En la Figura \(\PageIndex{3}\), \(ΔH\) representa la diferencia en entalpía entre los reactivos (\(A\) y \(B\)) y los productos (\(C\) y \( RE\)). La suma de \(E_a\) y \(ΔH\) representa la energía de activación para la reacción inversa:
\[C+D⟶A+B\]
Podemos usar la ecuación de Arrhenius para relacionar la energía de activación y el constante de velocidad, k, de una reacción dada:
\[k=Ae^{−E_a/RT} \label{Arrhenius}\]
En esta ecuación:
- \(R\) es el constante de gas ideal, que tiene un valor de 8.314 J/mol/K,
- \(T\) es la temperatura en la escala de Kelvin,
- \(E_a\) es la energía de activación en julios por mol,
- \(e\) es el constante 2.7183, y
- \(A\) es un constante llamado el factor de frecuencia, que está relacionado con la frecuencia de las colisiones y la orientación de las moléculas que reaccionan.
Ambos postulados de la teoría de colisión de las velocidades de reacción se acomodan en la ecuación de Arrhenius. El factor de frecuencia A está relacionado con la velocidad a la cual ocurren las colisiones que tienen la orientación correcta. El término exponencial, \(e^{-E_a/RT}\), está relacionado con la fracción de colisiones que proporciona energía adecuada para superar la barrera de activación de la reacción.
En un extremo, el sistema no contiene suficiente energía para que las colisiones superen la barrera de activación. En tales casos, no se produce una reacción. En el otro extremo, el sistema tiene tanta energía que cada colisión con la orientación correcta puede superar la barrera de activación y hacer que la reacción continúe. En tales casos, la reacción es casi instantánea.
La ecuación de Arrhenius (Ecuación \ref{Arrhenius}) describe cuantitativamente mucho de lo que ya hemos discutido sobre las velocidades de la reacción. Para dos reacciones a la misma temperatura, la reacción con la energía de activación más alta tiene la velocidad constante más baja y la velocidad más lenta. El valor más grande de \(E_a\) da como resultado un valor más pequeño para \(e^{-E_a/RT}\), lo que refleja la fracción más pequeña de moléculas con suficiente energía para reaccionar. Alternativamente, la reacción con el \(E_a\) más pequeño tiene una fracción más grande de moléculas con suficiente energía para reaccionar. Esto se reflejará como un valor mayor de \(e^{-E_a/RT}\), un constante de velocidad mayor y una velocidad más rápida para la reacción.
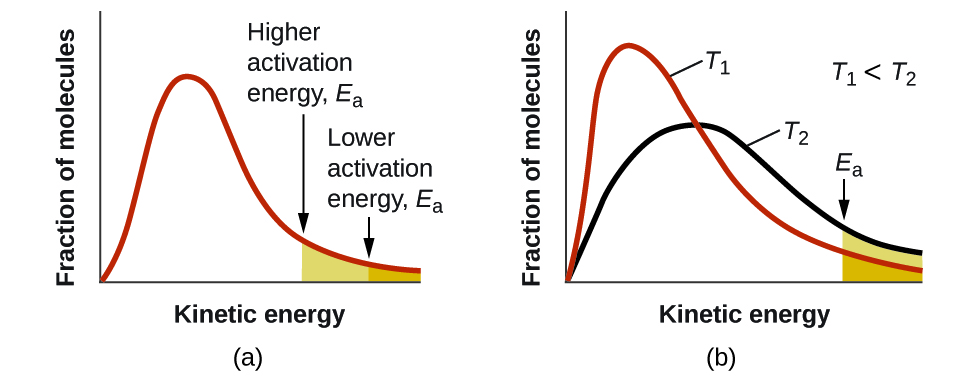
Un aumento en la temperatura tiene el mismo efecto que una disminución en la energía de activación. Una fracción mayor de moléculas tiene la energía necesaria para reaccionar (Figura \(\PageIndex{4}\)), como lo indica un aumento en el valor de \(e^{-E_a/RT}\). El constante de velocidad también es directamente proporcional al factor de frecuencia, \(A\). Por lo tanto, un cambio en las condiciones o reactivos que aumenta el número de colisiones con una orientación favorable para la reacción da como resultado un aumento en \(A\) y, en consecuencia, un aumento en \(k\).
Un enfoque conveniente para determinar \(E_a\) para una reacción implica la medición de \(k\) a diferentes temperaturas y el uso de una versión alternativa de la ecuación de Arrhenius que toma la forma de una ecuación lineal:
\ln k&=\left(\dfrac{−E_a}{R}\right)\left(\dfrac{1}{T}\right)+\ln A\\
y&=mx+b
\end{align*}\]
Por lo tanto, una gráfica de \(\lnk\) versus \(\dfrac{1}{T}\) da una línea recta con la pendiente \(\dfrac{E_\ce{a}}{R}\), a partir del cual se puede determinar Ea. La intersección da el valor de \(\lnA\). Esto a veces se llama un gráfico de Arrhenius.
Ejemplo \(\PageIndex{1}\)
La determinación de Ea:
La variación del constante de velocidad con la temperatura para la descomposición de HI(g) a H2(g) e I2(g) se da aquí. ¿Cuál es la energía de activación para la reacción?
\[\ce{2HI}(g)⟶\ce{H2}(g)+\ce{I2}(g)\]
| T (K) | k (L/mol/s) |
|---|---|
| 555 | 3.52 × 10−7 |
| 575 | 1.22 × 10−6 |
| 645 | 8.59 × 10−5 |
| 700 | 1.16 × 10−3 |
| 781 | 3.95 × 10−2 |
Solución
Los valores de \(\dfrac{1}{T}\) y ln k son:
| \(\mathrm{\dfrac{1}{T}\:(K^{−1})}\) | ln k |
|---|---|
| 1.80 × 10−3 | −14.860 |
| 1.74 × 10−3 | −13.617 |
| 1.55 × 10−3 | −9.362 |
| 1.43 × 10−3 | −6.759 |
| 1.28 × 10−3 | −3.231 |
Figura \(\PageIndex{5}\) es un gráfico de ln k versus \(\dfrac{1}{T}\). Para determinar la pendiente de la línea, necesitamos dos valores de ln k, que se determinan a partir de la línea en dos valores de \(\dfrac{1}{T}\) (es preferible uno cerca de cada extremo de la línea). Por ejemplo, el valor de ln k determinado a partir de la línea cuando \(\dfrac{1}{T}=1.25×10^{- 3}\) es −2.593; el valor cuando \(\dfrac{1}{T}=1.78×10^{- 3}\) es −14.447.
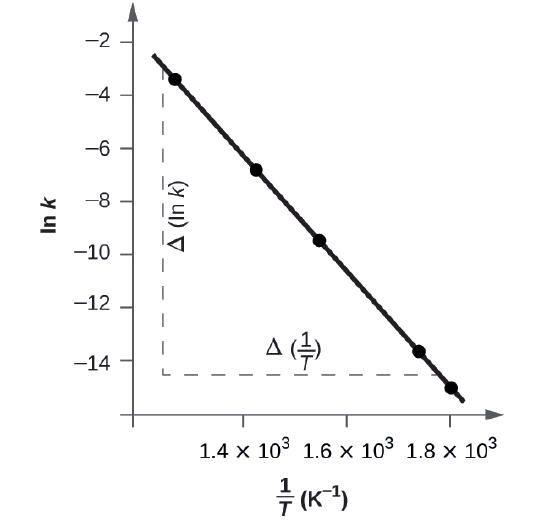
La pendiente de esta línea se da por la siguiente expresión
\[\begin{align*}\ce{Slope}&=\dfrac{Δ(\ln k)}{Δ\left(\dfrac{1}{T}\right)}\\
&=\mathrm{\dfrac{(−14.447)−(−2.593)}{(1.78×10^{−3}\:K^{−1})−(1.25×10^{−3}\:K^{−1})}}\\
&=\mathrm{\dfrac{−11.854}{0.53×10^{−3}\:K^{−1}}=2.2×10^4\:K}\\
&=−\dfrac{E_\ce{a}}{R}
\end{align*}\]
Así:
\[ \begin{align*} E_\ce{a} &=\mathrm{−slope×\mathit R=−(−2.2×10^4\:K×8.314\: J\: mol^{−1}\:K^{−1})} \\[5pt] &=\mathrm{1.8×10^5\:J\: mol^{−1}} \end{align*}\]
En muchas situaciones, es posible obtener una estimación razonable de la energía de activación sin pasar por todo el proceso de la construcción del gráfico de Arrhenius. La ecuación de Arrhenius se da como:
\[\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A \nonumber\]
se puede reorganizar como se muestra para dar:
\[\dfrac{Δ(\ln k)}{Δ\left(\dfrac{1}{T}\right)}=−\dfrac{E_\ce{a}}{R} \nonumber\]
o
\[\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right) \nonumber\]
Esta ecuación se puede reorganizar para dar un cálculo de un paso para obtener una estimación de la energía de activación:
\[E_\ce{a}=−R\left( \dfrac{\ln k_2−\ln k_1}{\left(\dfrac{1}{T_2}\right)−\left(\dfrac{1}{T_1}\right)}\right ) \nonumber \]
Usando los datos experimentales presentados aquí, simplemente podemos seleccionar dos entradas de datos. Para este ejemplo, seleccionamos la primera entrada y la última entrada:
| T (K) | k (L/mol/s) | \(\dfrac{1}{T}\:(K^{-1})\) | ln k |
|---|---|---|---|
| 555 | 3.52 × 10−7 | 1.80 × 10−3 | −14.860 |
| 781 | 3.95 × 10−2 | 1.28 × 10−3 | −3.231 |
Después de calcular \(\dfrac{1}{T}\) y ln k, podemos sustituir en la ecuación:
\[E_\ce{a}=\mathrm{−8.314\:J\:mol^{−1}\:K^{−1}\left(\dfrac{−3.231−(−14.860)}{1.28×10^{−3}\:K^{−1}−1.80×10^{−3}\:K^{−1}}\right)}\]
y el resultado es Ea = 185,900 J/mol.
Este método es muy efectivo, especialmente cuando hay disponible un número limitado de constantes de velocidad dependientes de la temperatura para la reacción de interés.
Ejercicio \(\PageIndex{1}\)
El constante de velocidad para la velocidad de descomposición de N2O5 en NO y O2 en la fase gaseosa es 1.66 L/mol/s a 650 K y 7.39 L/mol/s a 700 K:
\[\ce{2N2O5}(g)⟶\ce{4NO}(g)+\ce{3O2}(g) \nonumber\]
Suponiendo que la cinética de esta reacción sea consistente con la ecuación de Arrhenius, calcule la energía de activación para esta descomposición.
- Respuesta
-
113,000 J/mol
Resumen
Las reacciones químicas requieren colisiones entre especies reactivas. Estas colisiones de reactivos deben tener una orientación adecuada y suficiente energía para resultar en la formación del producto. La teoría de colisión nos da una explicación simple pero efectiva del efecto de muchos parámetros experimentales en las velocidades de la reacción. La ecuación de Arrhenius describe la relación entre el constante de velocidad de una reacción y su energía de activación, temperatura y dependencia de la orientación de la colisión.
Ecuaciones Clave
- \(k=Ae^{−E_a/RT}\)
- \(\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A\)
- \(\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right)\)
Glosario
- complejo activado
- (también, estado de transición) combinación inestable de especies reactivas que representan el estado de mayor energía de un sistema de reacción
- energía de activación (Ea)
- energía necesaria para que tenga lugar una reacción
- Ecuación de Arrhenius
- relación matemática entre el constante de velocidad y la energía de activación de una reacción
- teoría de colisión
- modelo que enfatiza la energía y la orientación de las colisiones moleculares para explicar y predecir la cinética de una reacción
- factor de frecuencia (A)
- constante de proporcionalidad en la ecuación de Arrhenius, relacionada con el número relativo de colisiones que tienen una orientación capaz de conducir a la formación del producto
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


