Carga Nuclear Efectiva
- Page ID
- 74869
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para Desarrollar
- Explicar la diferencia entre carga nuclear y carga nuclear efectiva
La razón por la que los electrones están unidos a los átomos es la atracción de la ley de Coulomb entre el núcleo cargado positivamente y los electrones cargados negativamente. Sin que la carga nuclear se aferrara a los electrones, no tendrían razón alguna para permanecer en orbitales cerca de núcleos. Entonces tiene sentido que la energía de los orbitales y su tamaño dependan de la carga nuclear. Por ejemplo, los orbitales equivalentes se vuelven más bajos en energía y más pequeños (más densidad más cerca del núcleo) cuando aumenta la carga nuclear. (Si quiere ver dónde está la carga nuclear en las ecuaciones orbitales, siga este enlace y haga clic en una órbita; luego desplácese hacia abajo para ver la ecuación. Z eff es la carga nuclear efectiva.)
Hay 2 razones por las que un electrón podría no pasar tanto tiempo en realidad justo al lado del núcleo, a pesar de que hay una atracción. Uno es el momento angular. Recuerda de la física que el momento angular es básicamente el impulso en la dirección “alrededor del centro” multiplicado por r, la distancia desde el centro. Así, si el electrón está “en” el núcleo, r = 0, y el momento angular es 0. Recuerde también que el segundo número cuántico es el número cuántico de momento angular l, que corresponde a los orbitales s, p, d y f. Para los orbitales s, l = 0, y el momento angular es cero, por lo que el electrón puede pasar el rato en el núcleo. Para las otras formas (p, d, f) el momento angular no es cero, y hay un nodo en el núcleo. Entonces solo los orbitales pueden pasar el rato justo en el núcleo.
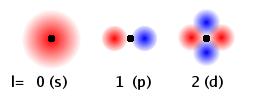
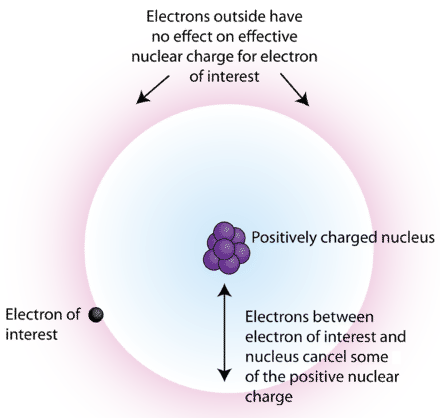
La otra razón por la que un electrón podría no ser capaz de acercarse tanto al núcleo es por los otros electrones. Los electrones se repelen entre sí, y debido al principio de exclusión solo puede haber 2 electrones en cada orbital. Entonces piensa en el litio, elemento 3. Sus primeros 2 electrones están en 1s. El tercer electrón está en 2s. Debido a que el número cuántico principal es mayor, el electrón 2s suele estar más lejos del núcleo que los electrones 1s. Eso significa que a menudo los electrones 1s están entre el electrón 2s y el núcleo. Esto significa que la atracción total de Coulomb que siente el electrón 2s es menor de lo que calcularía usando solo carga nuclear y distancia, porque también existe la repulsión electrón-electrón. Esta es la base de la carga nuclear efectiva. Debido a las repulsiones electrón-electrón, los electrones externos en un átomo de muchos electrones sienten menos atracción hacia el núcleo, por lo que sienten que la carga nuclear es más pequeña de lo que realmente es. Por lo que la carga nuclear efectiva es siempre menor que la carga nuclear real.
La carga nuclear efectiva depende del tipo de electrón. Los electrones en s orbitales, incluso 4s o 5s, todavía pasan algún tiempo justo en el núcleo, y cuando están ahí, sienten la carga nuclear completa, así que en promedio los electrones s sienten una carga nuclear más cercana a la carga nuclear real. Los electrones en los orbitales d o f realmente no se acercan mucho al núcleo, por lo que realmente se bloquean, o se blindan por electrones internos. Sienten una carga nuclear efectiva más pequeña que los electrones s. Y los electrones en p orbitales están en el medio.
Por lo general, si haces algún cálculo de orbitales para muchos átomos de electrones, usarás carga nuclear efectiva en lugar de carga nuclear real. El tamaño y la energía de los orbitales dependerán de la carga nuclear efectiva, no de la carga nuclear real. El tamaño y la energía de los orbitales determinan algunas propiedades químicas muy importantes, incluyendo el tamaño del elemento (como un átomo, ion o en una molécula) y la facilidad con la que pierde o gana electrones. Los electrones ocupan la mayor parte del espacio en un átomo, por lo que el tamaño orbital te indica el tamaño. La pérdida de electrones requiere la energía por la que están unidos, que es aproximadamente la misma que la energía orbital. Agregar electrones sólo funciona si el orbital a donde irán es menor energía que de donde vinieron.
Enlace exterior
- Carga Nuclear Efectiva (10 min)
Colaboradores y Atribuciones
Emily V Eames (City College of San Francisco)