9.2: Titulaciones ácido-Base
- Page ID
- 75439
Antes de 1800, la mayoría de las titulaciones ácido-base usaban H 2 SO 4, HCl o HNO 3 como titulantes ácidos, y K 2 CO 3 o Na 2 CO 3 como titulantes básicos. Se determinó el punto final de la titulación utilizando tornasol como indicador, el cual es rojo en soluciones ácidas y azul en soluciones básicas, o por el cese de la efervescencia de CO 2 al neutralizar\(\text{CO}_3^{2-}\). Los primeros ejemplos de titulación ácido-base incluyen determinar la acidez o alcalinidad de las soluciones y determinar la pureza de carbonatos y óxidos alcalinotérreos.
La determinación de acidez y alcalinidad continúan siendo aplicaciones importantes de la titrimetría ácido-base. Analizaremos más de cerca estas aplicaciones más adelante en esta sección.
Tres limitaciones frenaron el desarrollo de la titulación ácido-base: la falta de un valorador base fuerte para el análisis de ácidos débiles, la falta de indicadores adecuados y la ausencia de una teoría de la reactividad ácido-base. La introducción, en 1846, de NaOH como titulante de base fuerte extendió la titrimetría ácido-base a la determinación de ácidos débiles. La síntesis de tintes orgánicos proporcionó muchos indicadores nuevos. La fenolftaleína, por ejemplo, fue sintetizada por primera vez por Bayer en 1871 y utilizada como indicador de titulaciones ácido-base en 1877.
A pesar de la mayor disponibilidad de indicadores, la ausencia de una teoría de la reactividad ácido-base dificultó la selección de un indicador. El desarrollo de la teoría del equilibrio a finales del siglo XIX condujo a mejoras significativas en la comprensión teórica de la química ácido-base y, a su vez, de la titulación ácido-base. El establecimiento de la escala de pH por Sørenson en 1909 proporcionó un medio riguroso para comparar indicadores. La determinación de las constantes de disociación ácido-base permitió calcular una curva de titulación teórica, tal como lo esbozó Bjerrum en 1914. Por primera vez, los químicos analíticos tuvieron un método racional para seleccionar un indicador, haciendo de la titrimetría ácido-base una alternativa útil a la gravimetría.
Curvas de valoración ácido-base
En el resumen de este capítulo señalamos que el punto final de una titulación debe coincidir con su punto de equivalencia. Para entender la relación entre el punto final de una valoración ácido-base y su punto de equivalencia debemos saber cómo cambia el pH de la titulación durante una titulación. En esta sección aprenderemos a calcular una curva de titulación utilizando los cálculos de equilibrio del Capítulo 6. También aprenderemos a esbozar una buena aproximación de cualquier curva de valoración ácido-base utilizando un número limitado de cálculos simples.
Titulación de ácidos fuertes y bases fuertes
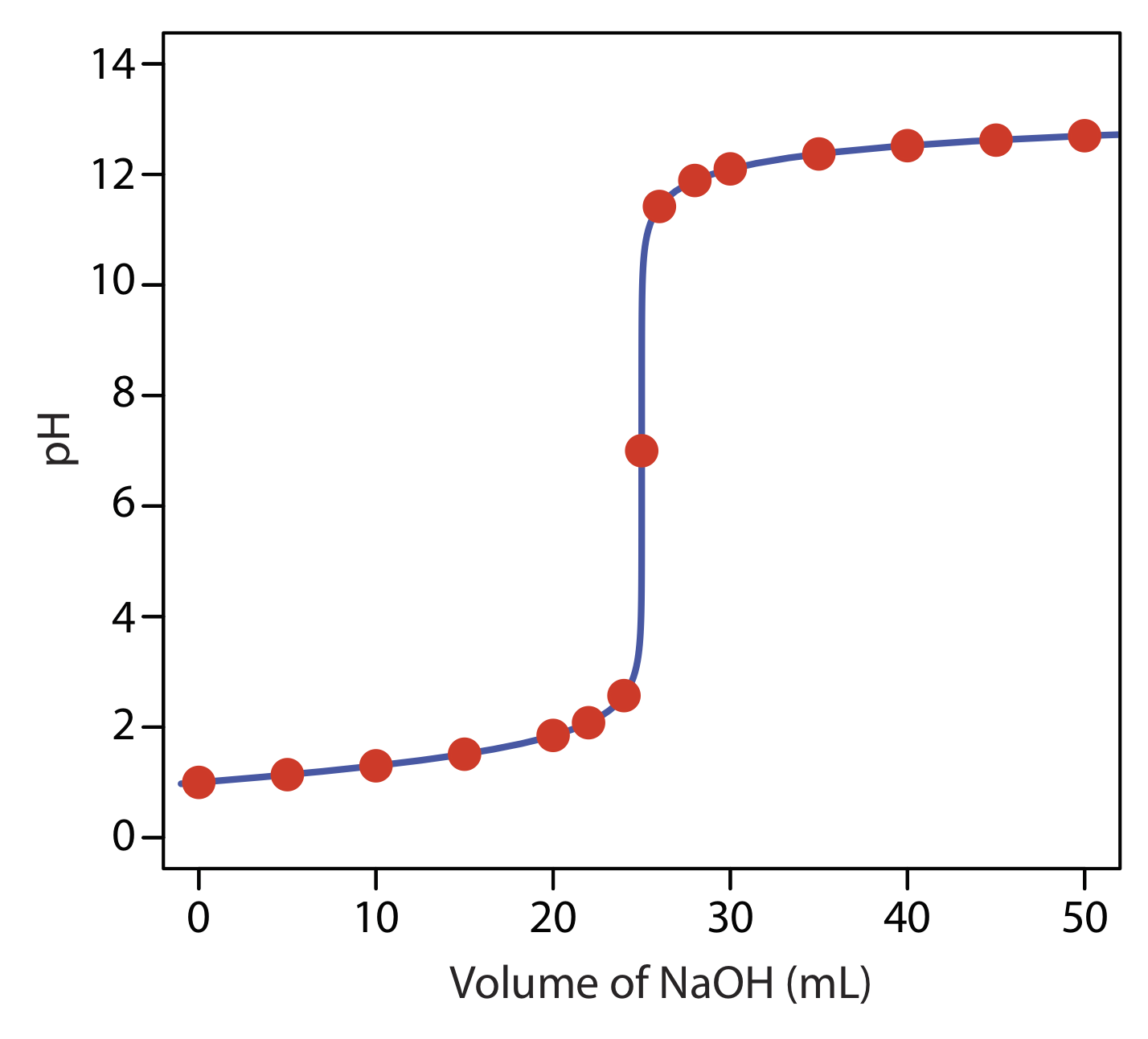
Para nuestra primera curva de valoración, consideremos la valoración de 50.0 mL de HCl 0.100 M usando un valorante de NaOH 0.200 M. Cuando una base fuerte y un ácido fuerte reaccionan la única reacción de importancia es
Aunque no hemos escrito la reacción\ ref {9.1} como una reacción de equilibrio, está en equilibrio; sin embargo, debido a que su constante de equilibrio es grande—es (Kw) —1 o\(1.00 \times 10^{14}\) —podemos tratar la reacción\ ref {9.1} como si fuera a su finalización.
La primera tarea es calcular el volumen de NaOH necesario para alcanzar el punto de equivalencia, V eq. En el punto de equivalencia sabemos por reacción\ ref {9.1} que
\[\begin{aligned} \text { moles } \mathrm{HCl}=& \text { moles } \mathrm{NaOH} \\ M_{a} \times V_{a} &=M_{b} \times V_{b} \end{aligned} \nonumber\]
donde el subíndice 'a' indica el ácido, HCl, y el subíndice 'b' indica la base, NaOH. El volumen de NaOH necesario para alcanzar el punto de equivalencia es
\[V_{e q}=V_{b}=\frac{M_{a} V_{a}}{M_{b}}=\frac{(0.100 \ \mathrm{M})(50.0 \ \mathrm{mL})}{(0.200 \ \mathrm{M})}=25.0 \ \mathrm{mL} \nonumber\]
Antes del punto de equivalencia, el HCl está presente en exceso y el pH se determina por la concentración de HCl sin reaccionar. Al inicio de la titulación la solución es de 0.100 M en HCl, lo que, debido a que el HCl es un ácido fuerte, significa que el pH es
\[\mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=-\log \left[\text{HCl} \right] = -\log (0.100)=1.00 \nonumber\]
Después de añadir 10.0 mL de NaOH, la concentración de HCl en exceso es
\[[\text{HCl}] = \frac {(\text{mol HCl})_\text{initial} - (\text{mol NaOH})_\text{added}} {\text{total volume}} = \frac {M_a V_a - M_b V_b} {V_a + V_b} \nonumber\]
\[[\mathrm{HCl}]=\frac{(0.100 \ \mathrm{M})(50.0 \ \mathrm{mL})-(0.200 \ \mathrm{M})(10.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+10.0 \ \mathrm{mL}}=0.0500 \ \mathrm{M} \nonumber\]
y el pH aumenta a 1.30.
En el punto de equivalencia los moles de HCl y los moles de NaOH son iguales. Dado que ni el ácido ni la base están en exceso, el pH está determinado por la disociación del agua.
\[\begin{array}{c}{K_{w}=1.00 \times 10^{-14}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}} \\ {\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=1.00 \times 10^{-7}}\end{array} \nonumber\]
Así, el pH en el punto de equivalencia es de 7.00.
Para volúmenes de NaOH mayores al punto de equivalencia, el pH está determinado por la concentración de exceso de OH —. Por ejemplo, después de agregar 30.0 mL de valorante la concentración de OH — es
\[[\text{OH}^-] = \frac {(\text{mol NaOH})_\text{added} - (\text{mol HCl})_\text{initial}} {\text{total volume}} = \frac {M_b V_b - M_a V_a} {V_a + V_b} \nonumber\]
\[\left[\mathrm{OH}^{-}\right]=\frac{(0.200 \ \mathrm{M})(30.0 \ \mathrm{mL})-(0.100 \ \mathrm{M})(50.0 \ \mathrm{mL})}{30.0 \ \mathrm{mL}+50.0 \ \mathrm{mL}}=0.0125 \ \mathrm{M} \nonumber\]
Para encontrar la concentración de H 3 O + utilizamos la expresión K w
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.00 \times 10^{-14}}{0.0125}=8.00 \times 10^{-13} \ \mathrm{M} \nonumber\]
para encontrar que el pH es de 12.10. La Tabla 9.2.1 y la Figura 9.2.1 muestran resultados adicionales para esta curva de titulación. Se puede utilizar este mismo enfoque para calcular la curva de titulación para la titulación de una base fuerte con un ácido fuerte, excepto que la base fuerte está en exceso antes del punto de equivalencia y el ácido fuerte está en exceso después del punto de equivalencia.
Construir una curva de titulación para la valoración de 25.0 mL de NaOH 0.125 M con HCl 0.0625 M.
- Responder
-
El volumen de HCl necesario para alcanzar el punto de equivalencia es
\[V_{e q}=V_{a}=\frac{M_{b} V_{b}}{M_{a}}=\frac{(0.125 \ \mathrm{M})(25.0 \ \mathrm{mL})}{(0.0625 \ \mathrm{M})}=50.0 \ \mathrm{mL} \nonumber\]
Antes del punto de equivalencia, el NaOH está presente en exceso y el pH se determina por la concentración de OH sin reaccionar —. Por ejemplo, después de añadir 10.0 mL de HCl
\[\begin{array}{c}{\left[\mathrm{OH}^{-}\right]=\frac{(0.125 \ \mathrm{M})(25.0 \ \mathrm{mL})-(0.0625 \mathrm{M})(10.0 \ \mathrm{mL})}{25.0 \ \mathrm{mL}+10.0 \ \mathrm{mL}}=0.0714 \ \mathrm{M}} \\ {\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{w}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.00 \times 10^{-14}}{0.0714 \ \mathrm{M}}=1.40 \times 10^{-13} \ \mathrm{M}}\end{array} \nonumber\]
el pH es 12.85.
Para la titulación de una base fuerte con un ácido fuerte el pH en el punto de equivalencia es de 7.00.
Para volúmenes de HCl mayores al punto de equivalencia, el pH está determinado por la concentración de HCl en exceso. Por ejemplo, después de agregar 70.0 mL de valorante, la concentración de HCl es
\[[\mathrm{HCl}]=\frac{(0.0625 \ \mathrm{M})(70.0 \ \mathrm{mL})-(0.125 \ \mathrm{M})(25.0 \ \mathrm{mL})}{70.0 \ \mathrm{mL}+25.0 \ \mathrm{mL}}=0.0132 \ \mathrm{M} \nonumber\]
dando un pH de 1.88. Aquí se muestran algunos resultados adicionales.
volumen de HCl (mL) pH volumen de HCl (mL) pH 0 13.10 60 2.13 10 12.85 70 1.88 20 12.62 80 1.75 30 12.36 90 1.66 40 11.98 100 1.60 50 7.00
Titulación de un ácido débil con una base fuerte
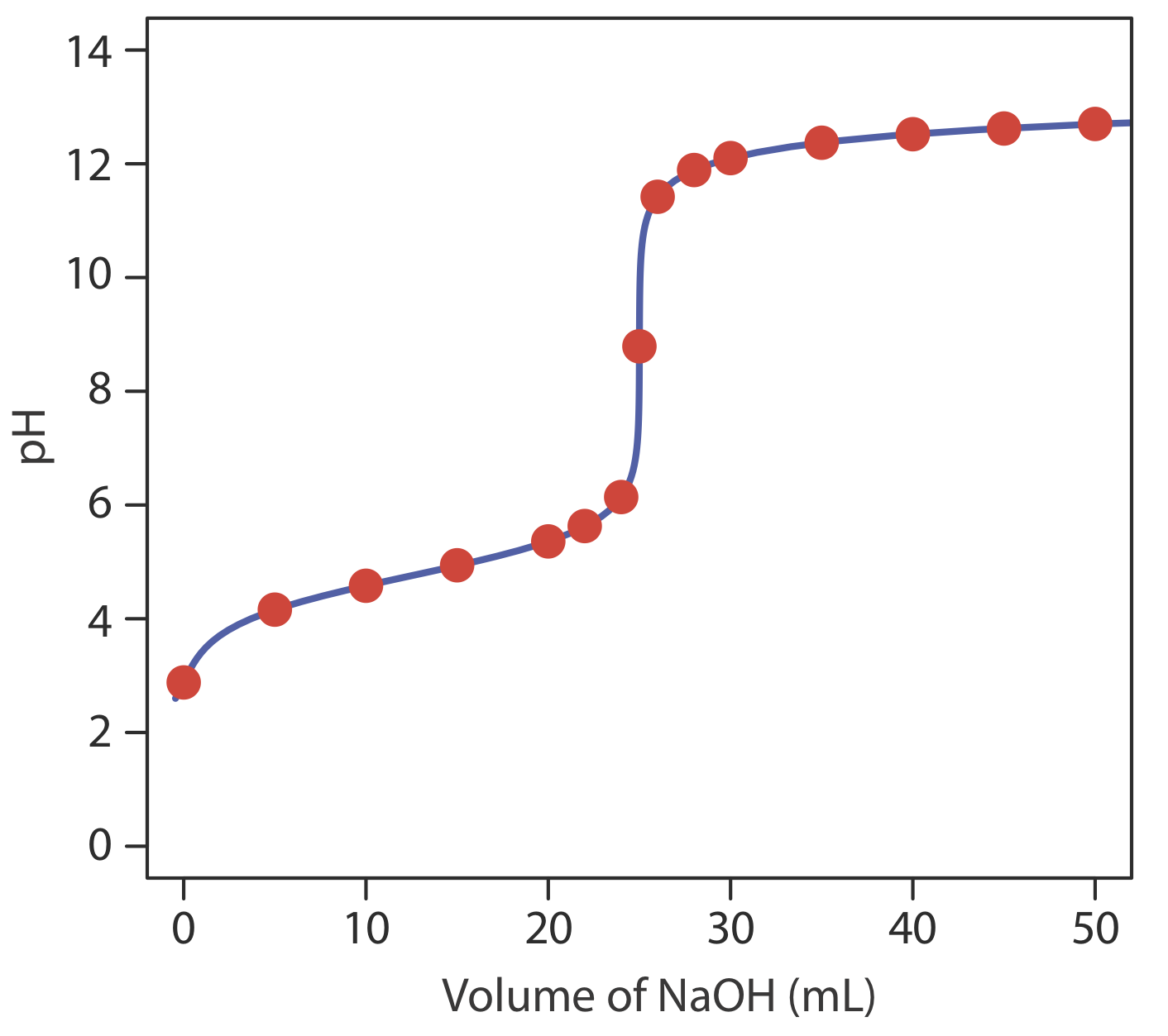
Para este ejemplo, consideremos la titulación de 50.0 mL de ácido acético 0.100 M, CH 3 COOH, con NaOH 0.200 M. Nuevamente, comenzamos calculando el volumen de NaOH necesario para alcanzar el punto de equivalencia; así
\[\operatorname{mol} \ \mathrm{CH}_{3} \mathrm{COOH}=\mathrm{mol} \ \mathrm{NaOH} \nonumber\]
\[M_{a} \times V_{a}=M_{b} \times V_{b} \nonumber\]
\[V_{e q}=V_{b}=\frac{M_{a} V_{a}}{M_{b}}=\frac{(0.100 \ \mathrm{M})(50.0 \ \mathrm{mL})}{(0.200 \ \mathrm{M})}=25.0 \ \mathrm{mL} \nonumber\]
Antes de comenzar la titulación el pH es el de una solución de ácido acético 0.100 M. Debido a que el ácido acético es un ácido débil, calculamos el pH usando el método descrito en el Capítulo 6
\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]
\[K_{a}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{CH}_{3} \mathrm{COO}^-\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}=\frac{(x)(x)}{0.100-x}=1.75 \times 10^{-5} \nonumber\]
encontrando que el pH es 2.88.
Al agregar NaOH se convierte una porción del ácido acético en su base conjugada, CH 3 COO —.
Porque la constante de equilibrio para la reacción\ ref {9.2} es bastante grande
\[K=K_{\mathrm{a}} / K_{\mathrm{w}}=1.75 \times 10^{9} \nonumber\]
podemos tratar la reacción como si fuera a su finalización.
Cualquier solución que contenga cantidades comparables de un ácido débil, HA, y su base débil conjugada, A —, es un tampón. Como aprendimos en el Capítulo 6, podemos calcular el pH de un tampón usando la ecuación de Henderson—Hasselbalch.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]} \nonumber\]
Antes del punto de equivalencia, la concentración de ácido acético sin reaccionar es
\[\left[\text{CH}_3\text{COOH}\right] = \frac {(\text{mol CH}_3\text{COOH})_\text{initial} - (\text{mol NaOH})_\text{added}} {\text{total volume}} = \frac {M_a V_a - M_b V_b} {V_a + V_b} \nonumber\]
y la concentración de acetato es
\[[\text{CH}_3\text{COO}^-] = \frac {(\text{mol NaOH})_\text{added}} {\text{total volume}} = \frac {M_b V_b} {V_a + V_b} \nonumber\]
Por ejemplo, después de agregar 10.0 mL de NaOH las concentraciones de CH 3 COOH y CH 3 COO — son
\[\left[\mathrm{CH}_{3} \mathrm{COOH}\right]=\frac{(0.100 \ \mathrm{M})(50.0 \ \mathrm{mL})-(0.200 \ \mathrm{M})(10.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+10.0 \ \mathrm{mL}} = 0.0500 \text{ M} \nonumber\]
\[\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=\frac{(0.200 \ \mathrm{M})(10.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+10.0 \ \mathrm{mL}}=0.0333 \ \mathrm{M} \nonumber\]
lo que nos da un pH de
\[\mathrm{pH}=4.76+\log \frac{0.0333 \ \mathrm{M}}{0.0500 \ \mathrm{M}}=4.58 \nonumber\]
En el punto de equivalencia los moles de ácido acético inicialmente presentes y los moles de NaOH añadidos son idénticos. Debido a que su reacción efectivamente avanza hasta su finalización, el ion predominante en solución es CH 3 COO —, que es una base débil. Para calcular el pH determinamos primero la concentración de CH 3 COO —
\[\left[\mathrm{CH}_{3} \mathrm{COO}^-\right]=\frac{(\mathrm{mol} \ \mathrm{NaOH})_{\mathrm{added}}}{\text { total volume }}= \frac{(0.200 \ \mathrm{M})(25.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+25.0 \ \mathrm{mL}}=0.0667 \ \mathrm{M} \nonumber\]
Alternativamente, podemos calcular la concentración de acetato usando los moles iniciales de ácido acético; así
\[\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]=\frac{\left(\mathrm{mol} \ \mathrm{CH}_{3} \mathrm{COOH}\right)_{\mathrm{initial}}}{\text { total volume }} = \frac{(0.100 \ \mathrm{M})(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+25.0 \ \mathrm{mL}} = 0.0667 \text{ M} \nonumber\]
A continuación, calculamos el pH de la base débil como se muestra anteriormente en el Capítulo 6
\[\mathrm{CH}_{3} \mathrm{COO}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{OH}^{-}(a q)+\mathrm{CH}_{3} \mathrm{COOH}(a q) \nonumber\]
\[K_{\mathrm{b}}=\frac{\left[\mathrm{OH}^{-}\right]\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}=\frac{(x)(x)}{0.0667-x}=5.71 \times 10^{-10} \nonumber\]
\[x=\left[\mathrm{OH}^{-}\right]=6.17 \times 10^{-6} \ \mathrm{M} \nonumber\]
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.00 \times 10^{-14}}{6.17 \times 10^{-6}}=1.62 \times 10^{-9} \ \mathrm{M} \nonumber\]
encontrando que el pH en el punto de equivalencia es de 8.79.
Después del punto de equivalencia, el valorante está en exceso y la mezcla de titulación es una solución diluida de NaOH. Podemos calcular el pH usando la misma estrategia que en la titulación de un ácido fuerte con una base fuerte. Por ejemplo, después de agregar 30.0 mL de NaOH la concentración de OH — es
\[\left[\mathrm{OH}^{-}\right]=\frac{(0.200 \ \mathrm{M})(30.0 \ \mathrm{mL})-(0.100 \ \mathrm{M})(50.0 \ \mathrm{mL})}{30.0 \ \mathrm{mL}+50.0 \ \mathrm{mL}}=0.0125 \ \mathrm{M} \nonumber\]
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.00 \times 10^{-14}}{0.0125}=8.00 \times 10^{-13} \ \mathrm{M} \nonumber\]
dando un pH de 12.10. La Tabla 9.2.2 y la Figura 9.2.2 muestran resultados adicionales para esta valoración. Se puede utilizar este mismo enfoque para calcular la curva de titulación para la titulación de una base débil con un ácido fuerte, excepto que el pH inicial está determinado por la base débil, el pH en el punto de equivalencia por su ácido débil conjugado, y el pH después del punto de equivalencia por exceso de ácido fuerte.
Construir una curva de titulación para la valoración de 25.0 mL de 0.125 M NH 3 con 0.0625 M HCl.
- Responder
-
El volumen de HCl necesario para alcanzar el punto de equivalencia es
\[V_{a q}=V_{a}=\frac{M_{b} V_{b}}{M_{a}}=\frac{(0.125 \ \mathrm{M})(25.0 \ \mathrm{mL})}{(0.0625 \ \mathrm{M})}=50.0 \ \mathrm{mL} \nonumber\]
Antes de añadir HCl el pH es el de una solución de 0.100 M NH 3.
\[K_{\mathrm{b}}=\frac{[\mathrm{OH}^-]\left[\mathrm{NH}_{4}^{+}\right]}{\left[\mathrm{NH}_{3}\right]}=\frac{(x)(x)}{0.125-x}=1.75 \times 10^{-5} \nonumber\]
\[x=\left[\mathrm{OH}^{-}\right]=1.48 \times 10^{-3} \ \mathrm{M} \nonumber\]
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{[\mathrm{OH}^-]}=\frac{1.00 \times 10^{-14}}{1.48 \times 10^{-3} \ \mathrm{M}}=6.76 \times 10^{-12} \ \mathrm{M} \nonumber\]
El pH al inicio de la titulación, por lo tanto, es de 11.17.
Antes del punto de equivalencia el pH es determinado por un\(\text{NH}_3/\text{NH}_4^+\) tampón. Por ejemplo, después de añadir 10.0 mL de HCl
\[\left[\mathrm{NH}_{3}\right]=\frac{(0.125 \ \mathrm{M})(25.0 \ \mathrm{mL})-(0.0625 \ \mathrm{M})(10.0 \ \mathrm{mL})}{25.0 \ \mathrm{mL}+10.0 \ \mathrm{mL}}=0.0714 \ \mathrm{M} \nonumber\]
\[\left[\mathrm{NH}_{4}^{+}\right]=\frac{(0.0625 \ \mathrm{M})(10.0 \ \mathrm{mL})}{25.0 \ \mathrm{mL}+10.0 \ \mathrm{mL}}=0.0179 \ \mathrm{M} \nonumber\]
\[\mathrm{pH}=9.244+\log \frac{0.0714 \ \mathrm{M}}{0.0179 \ \mathrm{M}}=9.84 \nonumber\]
En el punto de equivalencia el ion predominante en solución es\(\text{NH}_4^+\). Para calcular el pH primero determinamos la concentración de\(\text{NH}_4^+\)
\[\left[\mathrm{NH}_{4}^{+}\right]=\frac{(0.125 \ \mathrm{M})(25.0 \ \mathrm{mL})}{25.0 \ \mathrm{mL}+50.0 \ \mathrm{mL}}=0.0417 \ \mathrm{M} \nonumber\]
y luego calcular el pH
\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{NH}_{3}\right]}{\left[\mathrm{NH}_{4}^{+}\right]}=\frac{(x)(x)}{0.0417-x}=5.70 \times 10^{-10} \nonumber\]
obteniendo un valor de 5.31.
Después del punto de equivalencia, el pH es determinado por el exceso de HCl. Por ejemplo, después de agregar 70.0 mL de HCl
\[[\mathrm{HCl}]=\frac{(0.0625 \ \mathrm{M})(70.0 \ \mathrm{mL})-(0.125 \ \mathrm{M})(25.0 \ \mathrm{mL})}{70.0 \ \mathrm{mL}+25.0 \ \mathrm{mL}}=0.0132 \ \mathrm{M} \nonumber\]
y el pH es 1.88. Aquí se muestran algunos resultados adicionales.
volumen de HCl (mL) pH volumen de HCl (mL) pH 0 11.17 60 2.13 10 9.84 70 1.88 20 9.42 80 1.75 30 9.07 90 1.66 40 8.64 100 1.60 50 5.31
Podemos extender este enfoque para calcular una curva de titulación de base fuerte y ácido débil a reacciones que involucren ácidos o bases multipróticos, y mezclas de ácidos o bases. Sin embargo, a medida que aumenta la complejidad de la titulación, los cálculos necesarios consumen más tiempo. No es sorprendente que haya una variedad de enfoques algebraicos y de hojas de cálculo disponibles para ayudar a construir curvas de titulación.
Los siguientes artículos proporcionan información sobre enfoques algebraicos para el cálculo de curvas de titulación: (a) Willis, C. J. J. Chem. Educ. 1981, 58, 659—663; b) Nakagawa, K. J. Chem. Educ. 1990, 67, 673—676; c) Gordus, A. A. J. Chem. Educ. 1991, 68, 759—761; d) de Levie, R. J. Chem. Educ. 1993, 70, 209—217; e) Chaston, S. J. Chem. Educ. 1993, 70, 878—880; f) de Levie, R. Anal. Chem. 1996, 68, 585—590.
Los siguientes artículos proporcionan información sobre el uso de hojas de cálculo para generar curvas de titulación: a) Currie, J. O.; Whiteley, R. V. J. Chem. Educ. 1991, 68, 923—926; b) Brenemanan, G. L.; Parker, O. J. J. Chem. Educ. 1992, 69, 46—47; c) Carter, D. R.; Frye, M. S.; Mattson, W. A. J. Chem. Educ. 1993, 70, 67—71; d) Freiser, H. Conceptos y cálculos en química analítica, CRC Press: Boca Raton, 1992.
Croquizar una curva de valoración ácido-base
Para evaluar la relación entre el punto de equivalencia de una titulación y su punto final necesitamos construir solo una aproximación razonable de la curva de titulación exacta. En esta sección demostramos un método sencillo para esbozar una curva de titulación ácido-base. Nuestro objetivo es esbozar la curva de valoración rápidamente, utilizando el menor número posible de cálculos. Usemos la valoración de 50.0 mL de 0.100 M CH 3 COOH con NaOH 0.200 M para ilustrar nuestro enfoque. Este es el mismo ejemplo que usamos para desarrollar los cálculos de una curva de titulación de base fuerte y ácido débil. Puedes revisar los resultados de ese cálculo en la Tabla 9.2.2 y en la Figura 9.2.2 .
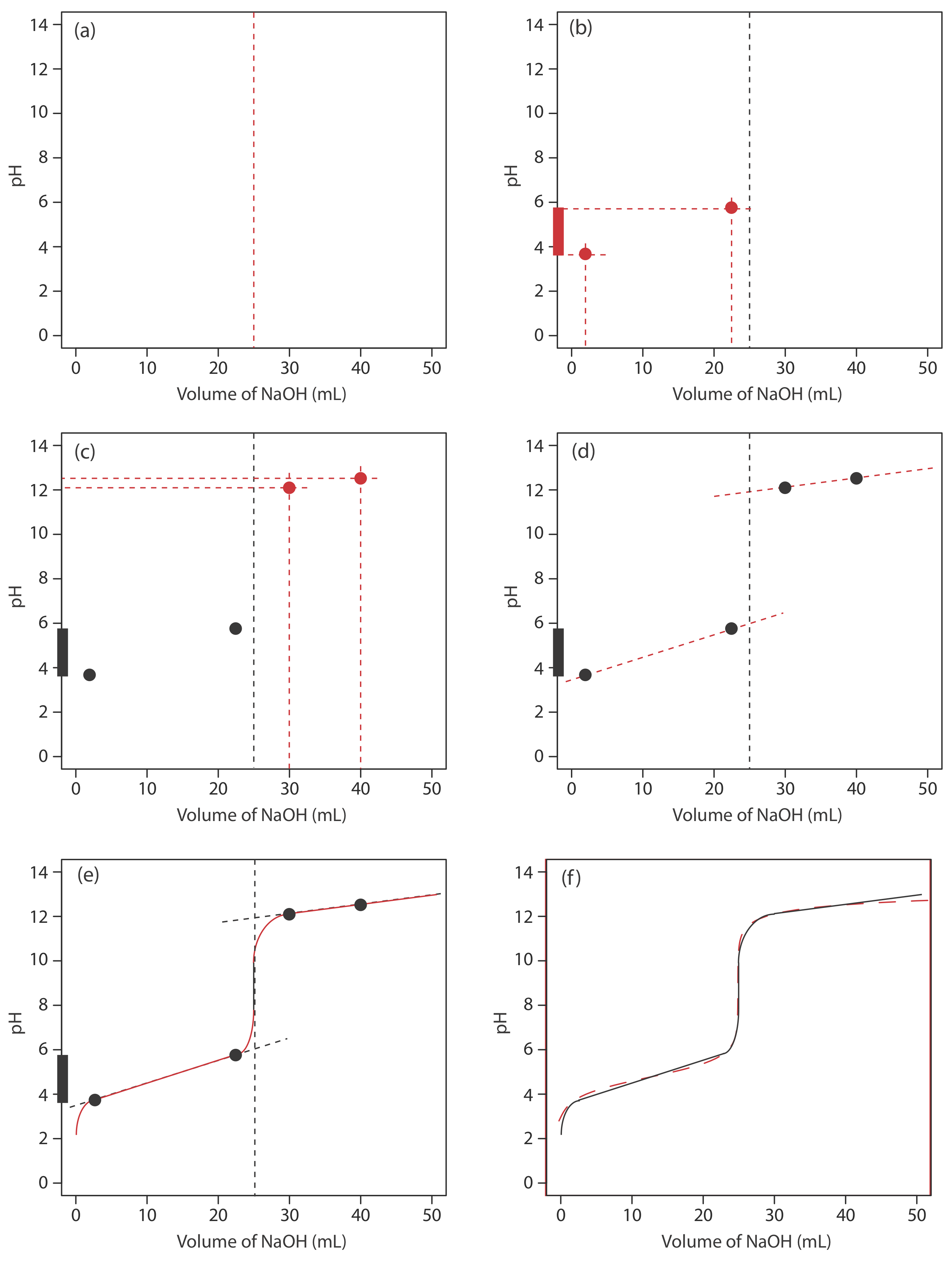
Comenzamos calculando el volumen del punto de equivalencia de la titulación, que, como determinamos anteriormente, es de 25.0 mL. A continuación dibujamos nuestros ejes, colocando el pH en el eje y y el volumen del valorante en el eje x. Para indicar el volumen del punto de equivalencia, dibujamos una línea vertical que cruza el eje x a 25.0 mL de NaOH. La figura 9.2.3 a muestra el primer paso en nuestro boceto.
Antes del punto de equivalencia el pH del titrand es determinado por un tampón de ácido acético, CH 3 COOH, y acetato, CH 3 COO —. Aunque podemos calcular el pH de un tampón usando la ecuación de Henderson—Hasselbalch, podemos evitar este cálculo haciendo una suposición simple. Puede recordar del Capítulo 6 que un tampón opera en un rango de pH que se extiende aproximadamente ±1 unidad de pH a cada lado del valor p K a del ácido débil. El pH se encuentra en el extremo inferior de este rango, pH = p K a — 1, cuando la concentración del ácido débil es\(10 \times\) mayor que la de su base débil conjugada. El tampón alcanza su límite de pH superior, pH = p K a + 1, cuando la concentración de ácido débil es\(10 \times\) menor que la de su base débil conjugada. Cuando valoramos un ácido débil o una base débil, el tampón abarca un rango de volúmenes desde aproximadamente 10% del volumen del punto de equivalencia hasta aproximadamente 90% del volumen del punto de equivalencia.
Los valores reales son 9.09% y 90.9%, pero para nuestro propósito, usar 10% y 90% es más conveniente; es decir, después de todo, ¡una ventaja de una aproximación!
La figura 9.2.3 b muestra el segundo paso de nuestro boceto. Primero, superponemos el diagrama de escalera de ácido acético en el eje y, incluyendo su rango de búfer, usando su valor p K a de 4.76. A continuación, agregamos dos puntos, uno para el pH al 10% del volumen del punto de equivalencia (un pH de 3.76 a 2.5 mL) y otro para el pH al 90% del volumen del punto de equivalencia (un pH de 5.76 a 22.5 mL).
El tercer paso es sumar dos puntos después del punto de equivalencia. El pH después del punto de equivalencia se fija por la concentración de exceso de titulante, NaOH. Calcular el pH de una base fuerte es sencillo, como vimos antes. Figura 9.2.3 c incluye puntos (ver Tabla 9.2.2 ) para el pH después de agregar 30.0 mL y después de agregar 40.0 mL de NaOH.
A continuación, dibujamos una línea recta a través de cada par de puntos, extendiendo cada línea a través de la línea vertical que representa el volumen del punto de equivalencia (Figura 9.2.3 d). Finalmente, completamos nuestro boceto dibujando una curva suave que conecta los tres segmentos de línea recta (Figura 9.2.3 e). Una comparación de nuestro boceto con la curva de titulación exacta (Figura 9.2.3 f) muestra que están muy de acuerdo.
Dibuje una curva de titulación para la titulación de 25.0 mL de 0.125 M NH 3 con 0.0625 M HCl y compárela con el resultado del Ejercicio 9.2.2 .
- Responder
-
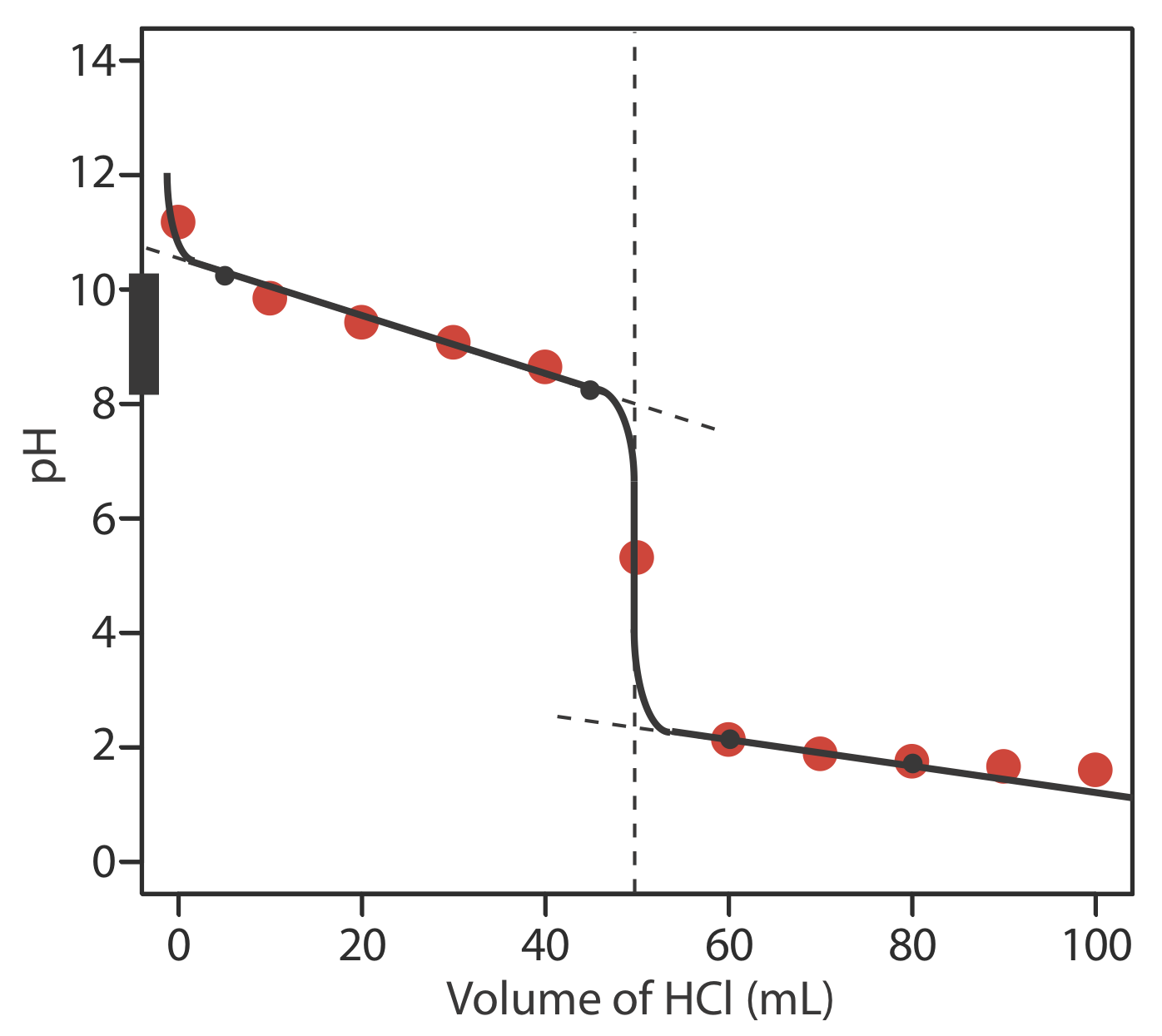
En la siguiente figura se muestra un boceto de la curva de titulación. Los puntos negros y la curva son el boceto aproximado de la curva de titulación. Los puntos en rojo son los cálculos del Ejercicio 9.2.2 . Los dos puntos negros antes del punto de equivalencia (V HCl = 5 mL, pH = 10.24 y V HCl = 45 mL, pH= 8.24) se trazan usando el p K a de 9.244 para\(\text{NH}_4^+\). Los dos puntos negros después del punto de equivalencia (V HCl = 60 mL, pH = 2.13 y V HCl = 80 mL, pH= 1.75) son de la respuesta al Ejercicio 9.2.2 .
Como se muestra en el siguiente ejemplo, podemos adaptar este enfoque a cualquier titulación ácido-base, incluyendo aquellos donde los cálculos exactos son más desafiantes, incluyendo la titulación de ácidos débiles polipróticos y bases, y la valoración de mezclas de ácidos débiles o bases débiles.
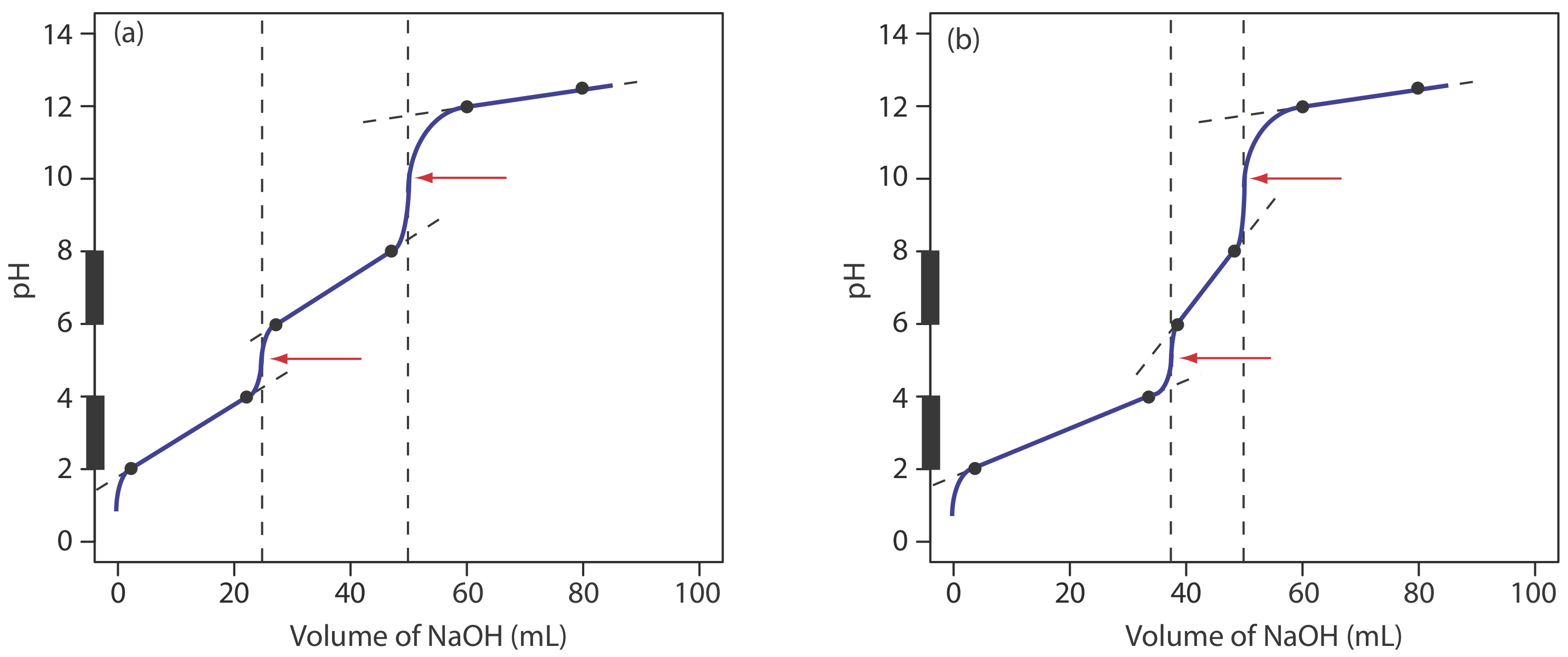
Esbozar las curvas de valoración para los dos sistemas siguientes: (a) la titulación de 50.0 mL de 0.050 M H 2 A, un ácido débil diprótico con un p K a1 de 3 y un p K a2 de 7; y (b) la titulación de una mezcla de 50.0 mL que contiene 0.075 M HA, un ácido débil con un p K a de 3, y 0.025 M HB, un ácido débil con una p K a de 7. Para ambas titulaciones, supongamos que el valorante es NaOH 0.10 M.
Solución
La Figura 9.2.4 a muestra la curva de valoración para H 2 A, incluyendo el diagrama de escalera para H 2 A en el eje y, los dos puntos de equivalencia a 25.0 mL y a 50.0 mL, dos puntos antes de cada punto de equivalencia, dos puntos después del último punto de equivalencia, y el líneas rectas utilizadas para bosquejar la curva de valoración final. Antes del primer punto de equivalencia el pH es controlado por un tampón de H 2 A y HA —. Un tampón HA — /A 2— controla el pH entre los dos puntos de equivalencia. Después del segundo punto de equivalencia el pH refleja la concentración de exceso de NaOH.
La Figura 9.2.4 b muestra la curva de titulación para la mezcla de HA y HB. Nuevamente, hay dos puntos de equivalencia; sin embargo, en este caso los puntos de equivalencia no están igualmente espaciados porque la concentración de HA es mayor que la de HB. Debido a que el HA es el más fuerte de los dos ácidos débiles reacciona primero; así, el pH antes del primer punto de equivalencia es controlado por un tampón de HA y A —. Entre los dos puntos de equivalencia el pH refleja la titulación de HB y está determinado por un tampón de HB y B —. Después del segundo punto de equivalencia, el exceso de NaOH determina el pH.
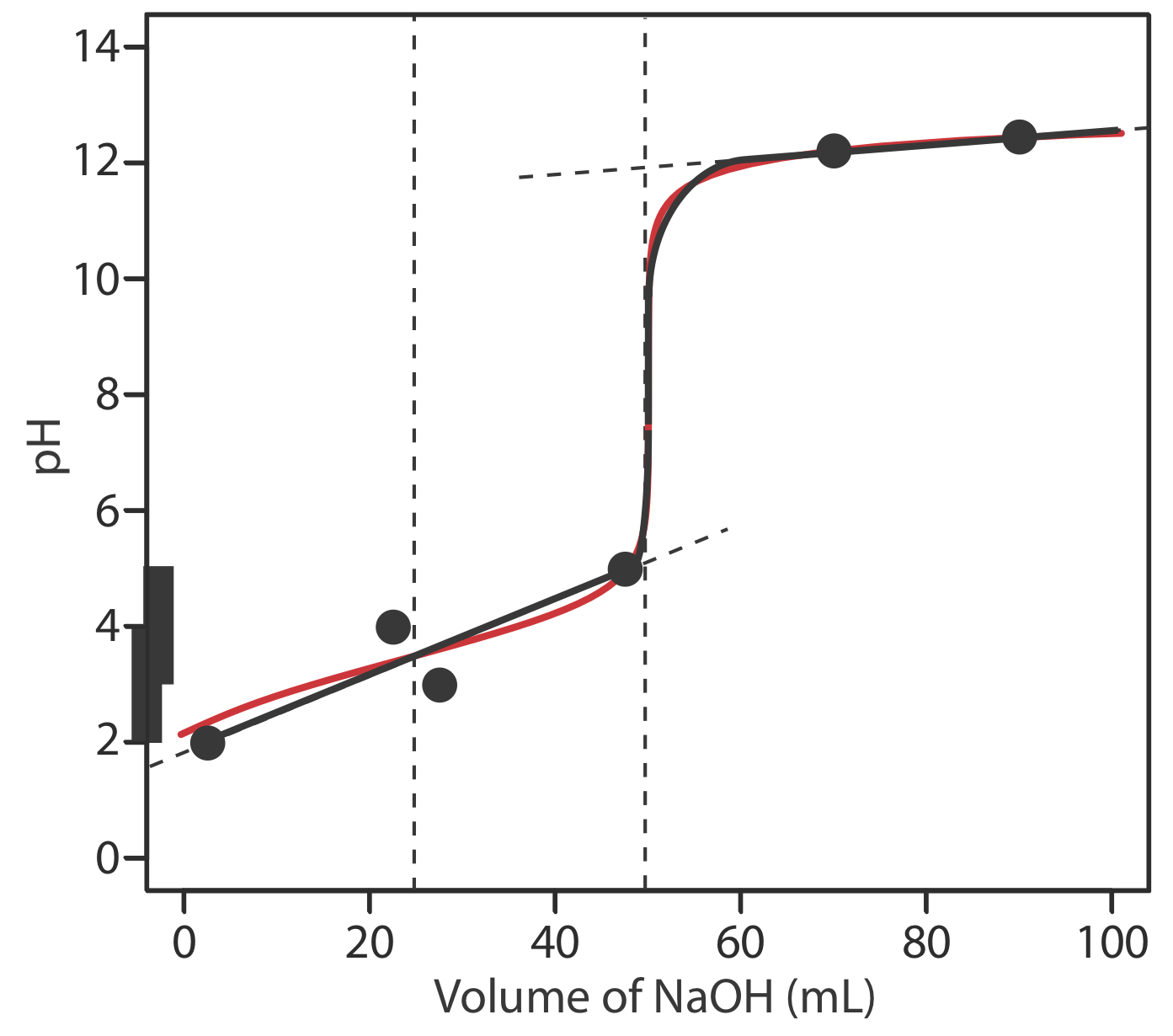
Esbozar la curva de titulación para 50.0 mL de 0.050 M H 2 A, un ácido débil diprótico con un p K a1 de 3 y un p K a2 de 4, utilizando NaOH 0.100 M como valorante. El hecho de que p K a2 se encuentre dentro del rango de búfer de p K a1 presenta un desafío que deberá considerar.
- Responder
-
En la siguiente figura se muestra un boceto de la curva de titulación. La curva de titulación tiene dos puntos de equivalencia, uno a 25.0 mL\((\text{H}_2\text{A} \rightarrow \text{HA}^-)\) y otro a 50.0 mL (\(\text{HA}^- \rightarrow \text{A}^{2-}\)). Al esbozar la curva, trazamos dos puntos antes del primer punto de equivalencia usando la p K a1 de 3 para H 2 A
\[V_{\mathrm{HCl}}=2.5 \ \mathrm{mL}, \mathrm{pH}=2 \text { and } V_{\mathrm{HCl}}=22.5 \ \mathrm{mL}, \mathrm{pH}=4 \nonumber\]
dos puntos entre los puntos de equivalencia usando la p K a2 de 5 para HA —
\[V_{\mathrm{HCl}}=27.5 \ \mathrm{mL}, \mathrm{pH}=3, \text { and } V_{\mathrm{HCl}}=47.5 \ \mathrm{mL}, \mathrm{pH}=5 \nonumber\]
y dos puntos después del segundo punto de equivalencia
\[V_{\mathrm{HCl}}=70 \ \mathrm{mL}, \mathrm{pH}=12.22 \text { and } V_{\mathrm{HCl}}=90 \ \mathrm{mL}, \mathrm{pH}=12.46 \nonumber\]
Dibujar una curva suave a través de estos puntos nos presenta el siguiente dilema: el pH parece aumentar a medida que el volumen del valorante se acerca al primer punto de equivalencia y luego parece disminuir a medida que pasa por el primer punto de equivalencia. Esto es, por supuesto, absurdo; a medida que agregamos NaOH el pH no puede disminuir. En cambio, modelizamos la curva de titulación antes del segundo punto de equivalencia dibujando una línea recta desde el primer punto (V HCl = 2.5 mL, pH = 2) hasta el cuarto punto (V HCl = 47.5 mL, pH= 5), ignorando el segundo y tercer punto. El resultado es una aproximación razonable de la curva de titulación exacta.
Selección y Evaluación del Punto Final
Anteriormente hicimos una distinción importante entre el punto final de una titulación y su punto de equivalencia. La diferencia entre estos dos términos es importante y merece repetirse. Un punto de equivalencia, que ocurre cuando reaccionamos estequiométricamente cantidades iguales del analito y el valorante, es un valor teórico no experimental. El punto final de una titulación es un resultado experimental que representa nuestra mejor estimación del punto de equivalencia. Cualquier diferencia entre el punto de equivalencia de una titulación y su punto final correspondiente es una fuente de error determinado.
¿Dónde está el Punto de Equivalencia?
Anteriormente aprendimos a calcular el pH en el punto de equivalencia para la titulación de un ácido fuerte con una base fuerte, y para la valoración de un ácido débil con una base fuerte. También aprendimos a trazar una curva de titulación con solo un mínimo de cálculos. También podemos localizar el punto de equivalencia sin realizar ningún cálculo. La respuesta, como puedes adivinar, ¡muchas veces es sí!
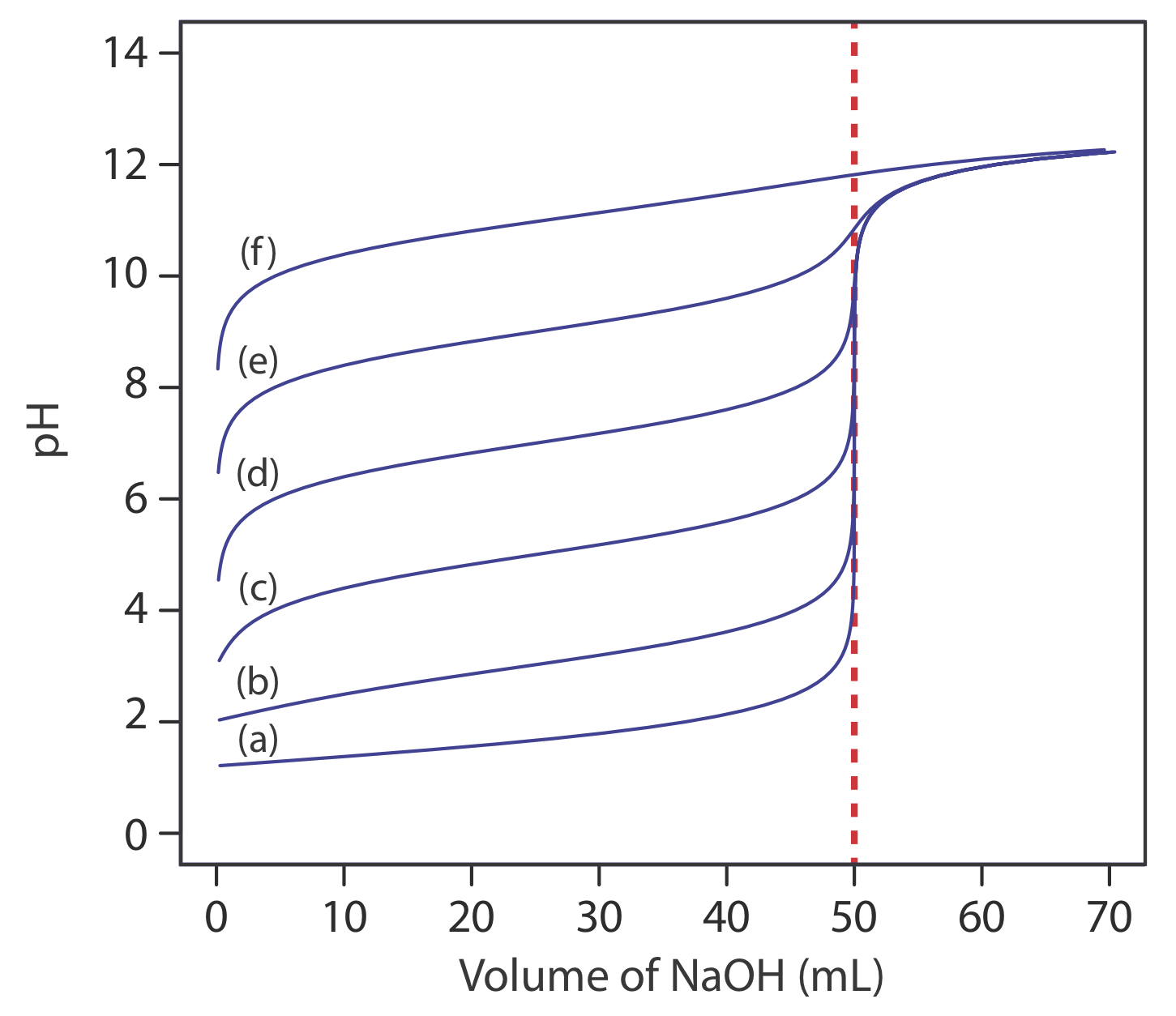
Para la mayoría de las valoraciones ácido-base, el punto de inflexión, el punto en una curva de valoración que tiene la mayor pendiente, casi coincide con el punto de equivalencia de la titulación. Las flechas rojas en la Figura 9.2.4 , por ejemplo, identifican los puntos de equivalencia para las curvas de titulación en el Ejemplo 9.2.1 . Un punto de inflexión en realidad precede a su correspondiente punto de equivalencia en una pequeña cantidad, con el error acercándose a 0.1% para ácidos débiles y bases débiles con constantes de disociación menores a 10 —9, o para soluciones muy diluidas [Meites, L.; Goldman, J. A. Anal. Chim. Acta 1963, 29, 472—479].
La principal limitación de un punto de inflexión es que debe estar presente y ser fácil de identificar. Para algunas titulaciones falta el punto de inflexión o es difícil de encontrar. La Figura 9.2.5 , por ejemplo, demuestra el efecto de la constante de disociación de un ácido débil, K a, en la forma de su curva de titulación. Un punto de inflexión es visible, aunque apenas sea así, para constantes de disociación ácida mayores a 10 —9, pero falta cuando K a es 10 —11.
También puede faltar un punto de inflexión o ser difícil de ver si el analito es un ácido débil multiprótico o una base débil con constantes de disociación sucesivas que son similares en magnitud. Para apreciar por qué esto es cierto consideremos la titulación de un ácido débil diprótico, H 2 A, con NaOH. Durante la titulación se producen las siguientes dos reacciones.
Para ver dos puntos de inflexión distintos, la reacción\ ref {9.3} debe estar esencialmente completa antes de que comience la reacción\ ref {9.4}.
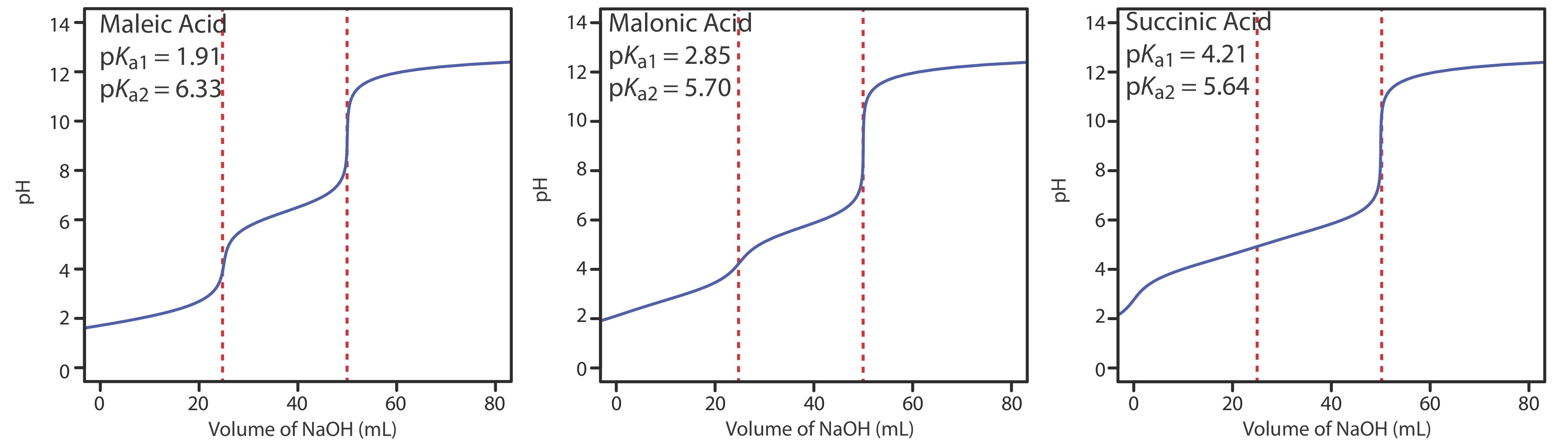
La Figura 9.2.6 muestra curvas de titulación para tres ácidos débiles dipróticos. La curva de valoración para el ácido maleico, para la cual K a1 es aproximadamente\(20000 \times\) mayor que K a2, tiene dos puntos de inflexión distintos. El ácido malónico, por otro lado, tiene constantes de disociación ácida que difieren en un factor de aproximadamente 690. Aunque la curva de valoración del ácido malónico muestra dos puntos de inflexión, el primero no es tan distinto como el segundo. Finalmente, la curva de titulación para el ácido succínico, para la cual los dos valores de K a difieren por un factor de solo\(27 \times\), tiene sólo un único punto de inflexión que corresponde a la neutralización de\(\text{HC}_2\text{H}_4\text{O}_4^-\) a\(\text{C}_2\text{H}_4\text{O}_4^{2-}\). En general, podemos detectar puntos de inflexión separados cuando las constantes sucesivas de disociación ácida difieren en un factor de al menos 500 (una\(\Delta\) K a de al menos 2.7).
Lo mismo es válido para mezclas de ácidos débiles o mezclas de bases débiles. Para detectar puntos de inflexión separados al valorar una mezcla de ácidos débiles, sus valores p K a deben diferir en al menos un factor de 500.
Encontrar el punto final con un indicador
Un grupo interesante de ácidos débiles y bases débiles son los colorantes orgánicos. Debido a que un tinte orgánico tiene al menos una especie conjugada ácido-base altamente coloreada, su titulación da como resultado un cambio tanto en su pH como en su color. Podemos usar este cambio de color para indicar el punto final de una titulación siempre que ocurra en o cerca del punto de equivalencia de la titulación.
Como ejemplo, consideremos un indicador para el cual la forma ácida, hIN, es amarilla y la forma base, In —, es roja. El color de la solución del indicador depende de las concentraciones relativas de hIN e In —. Para entender la relación entre pH y color utilizamos la reacción de disociación ácida del indicador
\[\mathrm{HIn}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\operatorname{In}^{-}(a q) \nonumber\]
y su expresión constante de equilibrio.
Tomando el log negativo de cada lado de la Ecuación\ ref {9.5}, y reordenarlo para resolver el pH nos deja con una ecuación que relaciona el pH de la solución con las concentraciones relativas de Hin e In —.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{[\mathrm{In}^-]}{[\mathrm{HIn}]} \label{9.6}\]
Si podemos detectar hIN e In —con igual facilidad, entonces la transición de amarillo a rojo (o de rojo a amarillo) alcanza su punto medio, que es naranja, cuando las concentraciones de hIN e In — son iguales, o cuando el pH es igual al p K a del indicador. Si el p K a del indicador y el pH en el punto de equivalencia son idénticos, entonces valorar hasta que el indicador se vuelva naranja es un punto final adecuado. Desafortunadamente, rara vez conocemos el pH exacto en el punto de equivalencia. Además, determinar cuándo son iguales las concentraciones de HiN e In — es difícil si el cambio de color del indicador es sutil.
Podemos establecer el rango de pH sobre el cual el analista promedio observa un cambio en el color del indicador haciendo dos suposiciones: que el color del indicador es amarillo si la concentración de hIN es\(10 \times\) mayor que la de In — y que su color es rojo si la concentración de hIN es \(10 \times\)menor que la de In —. Sustituyendo estas desigualdades en la Ecuación\ ref {9.6}
\[\begin{array}{l}{\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{1}{10}=\mathrm{p} K_{\mathrm{a}}-1} \\ {\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{10}{1}=\mathrm{p} K_{\mathrm{a}}+1}\end{array} \nonumber\]
muestra que el indicador cambia de color en un rango de pH que se extiende ±1 unidad a cada lado de su p K a. Como se muestra en la Figura 9.2.7 , el indicador es amarillo-ow cuando el pH es menor que p K a — 1 y es rojo cuando el pH es mayor que p K a + 1. Para valores de pH entre p K a — 1 y p K a + 1 el color del indicador pasa por varios tonos de naranja. Las propiedades de varios indicadores ácido-base comunes se enumeran en la Tabla 9.2.3 .
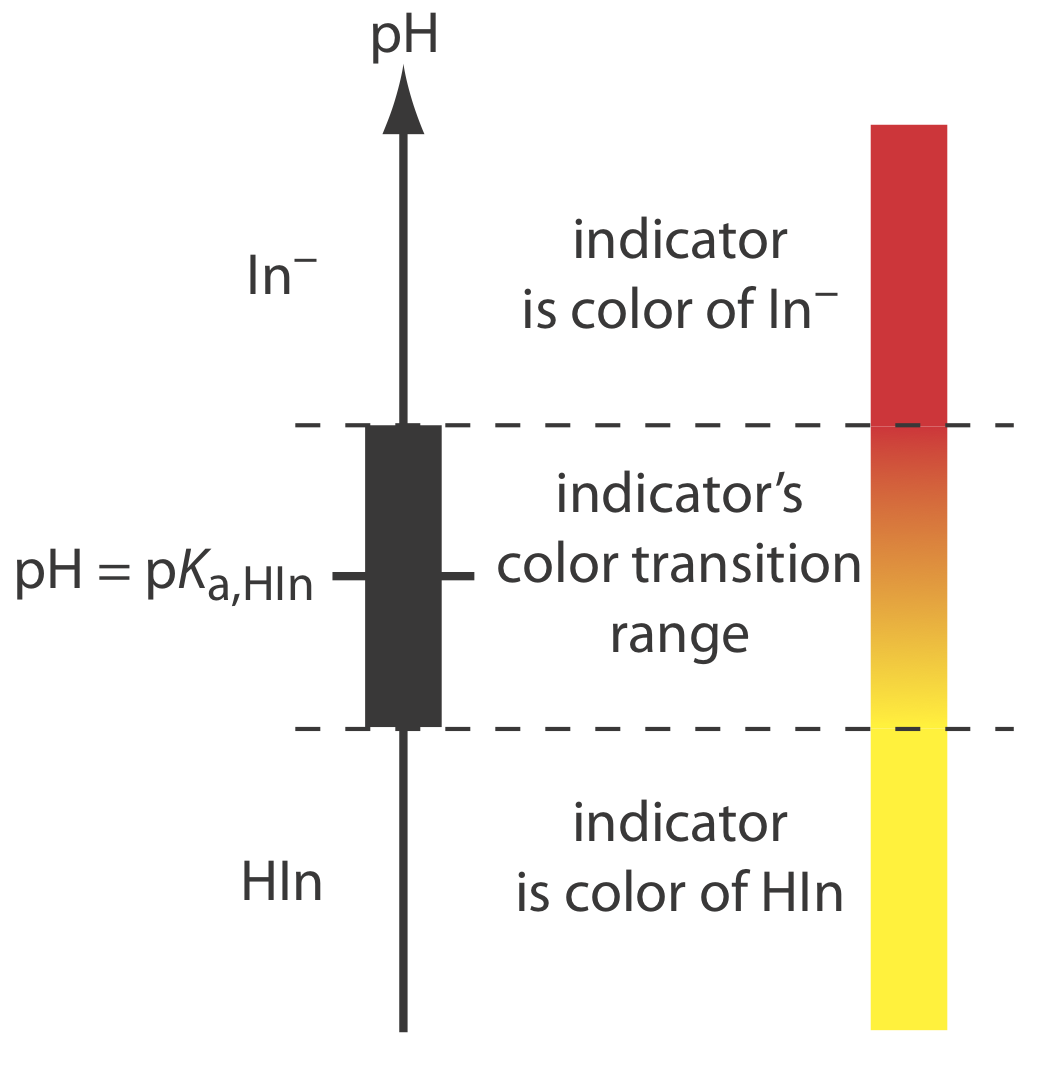
Quizás se pregunte por qué el rango de pH de un indicador, como el de la fenolftaleína, no se distribuye equitativamente alrededor de su valor p K a. La explicación es sencilla. La figura 9.2.7 presenta una vista idealizada en la que nuestra sensibilidad a los dos colores del indicador es igual. Para algunos indicadores solo se colorea el ácido débil o la base débil. Para otros indicadores tanto el ácido débil como la base débil están coloreados, pero una forma es más fácil de ver. En cualquier caso, el rango de pH del indicador está sesgado en la dirección de la forma menos coloreada del indicador. Así, el rango de pH de la fenolftaleína está sesgado en la dirección de su forma incolora, desplazando el rango de pH a valores inferiores a los sugeridos por la Figura 9.2.7 .
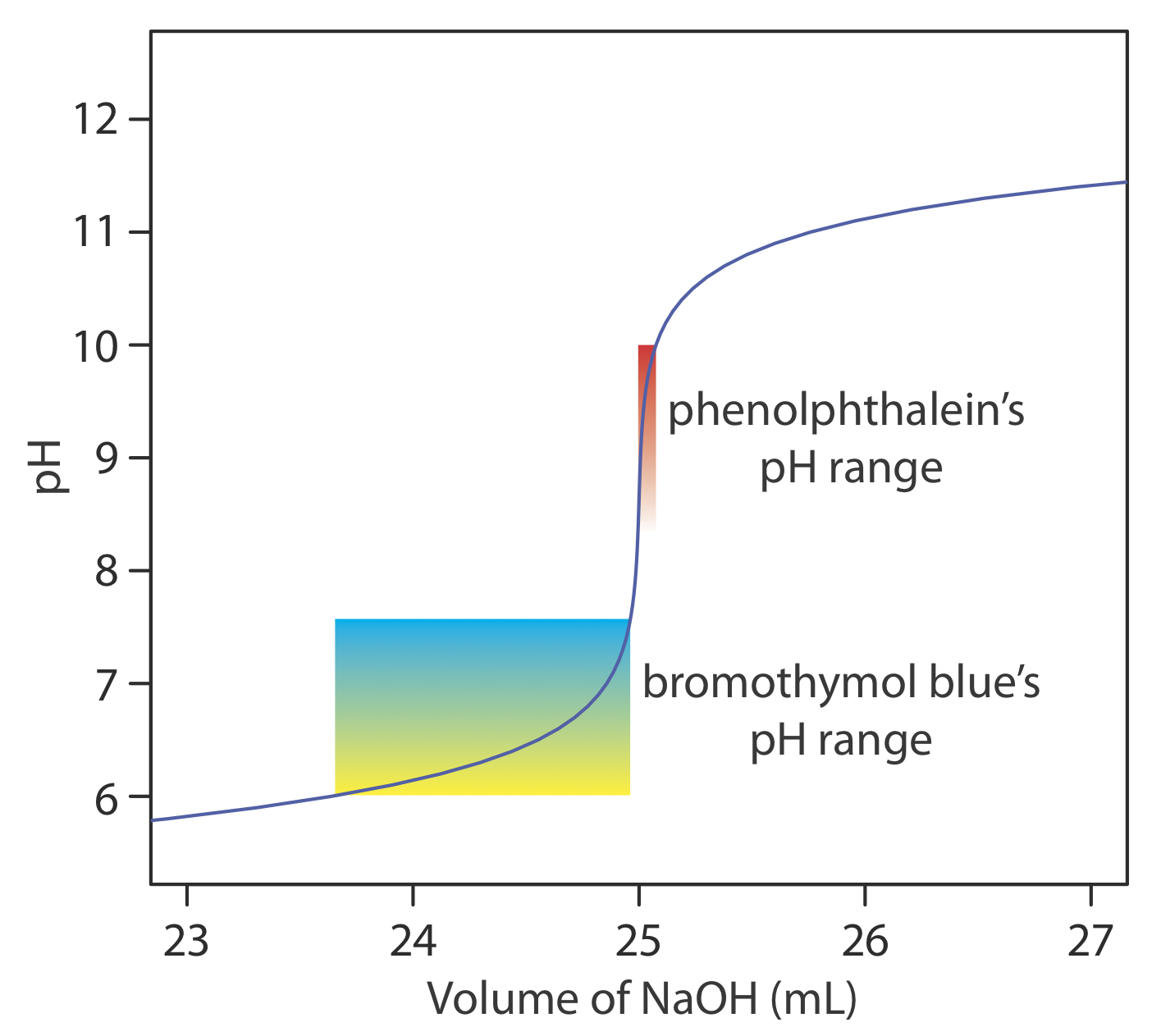
El rango relativamente amplio de pH sobre el cual un indicador cambia de color pone limitaciones adicionales en su capacidad para señalar el punto final de una titulación. Para minimizar un determinado error de valoración, todo el rango de pH del indicador debe estar dentro del cambio rápido en el pH cerca del punto de equivalencia. Por ejemplo, en la Figura {{template.index (ID:8)} vemos que la fenolftaleína es un indicador apropiado para la titulación de 50.0 mL de ácido acético 0.050 M con NaOH 0.10 M. El azul de bromotimol, por otro lado, es un indicador inapropiado porque su cambio de color comienza mucho antes del fuerte aumento inicial del pH, y, como resultado, abarca un rango relativamente grande de volúmenes. El cambio temprano en el color aumenta la probabilidad de obtener un resultado inexacto, y el rango de posibles volúmenes de punto final aumenta la probabilidad de obtener resultados imprecisos.
Sugerir un indicador adecuado para la titulación de 25.0 mL de 0.125 M NH 3 con NaOH 0.0625 M. Construiste una curva de valoración para esta valoración en Ejercicio 9.2.2 y Ejercicio 9.2.3 .
- Responder
-
El pH en el punto de equivalencia es de 5.31 (ver Ejercicio 9.2.2 ) y la parte afilada de la curva de titulación se extiende desde un pH de aproximadamente 7 hasta un pH de aproximadamente 4. De los indicadores de la Tabla 9.2.3 , el rojo de metilo es la mejor opción porque su p K un valor de 5.0 es el más cercano al pH del punto de equivalencia y porque el rango de pH de 4.2—6.3 para su cambio de color no producirá un error de titulación significativo.
Encontrar el punto final mediante el monitoreo del pH
Un enfoque alternativo para localizar el punto final de una titulación es monitorear el progreso de la titulación usando un sensor cuya señal es una función de la concentración del analito. El resultado es una gráfica de toda la curva de titulación, que podemos usar para ubicar el punto final con un error mínimo.
Un electrodo de pH es el sensor obvio para monitorear una titulación ácido-base y el resultado es una curva de titulación potenciométrica. Por ejemplo, la Figura {{template.index (ID:9)} a muestra una pequeña porción de la curva de titulación potenciométrica para la titulación de 50.0 mL de 0.050 M CH 3 COOH con NaOH 0.10 M, la cual se enfoca en la región que contiene el punto de equivalencia. El método más simple para encontrar el punto final es ubicar el punto de inflexión de la curva de titulación, que se muestra con la flecha. Este es también el método menos preciso, particularmente si la curva de titulación tiene una pendiente poco profunda en el punto de equivalencia.
Consulte el Capítulo 11 para obtener más detalles sobre los electrodos de pH.
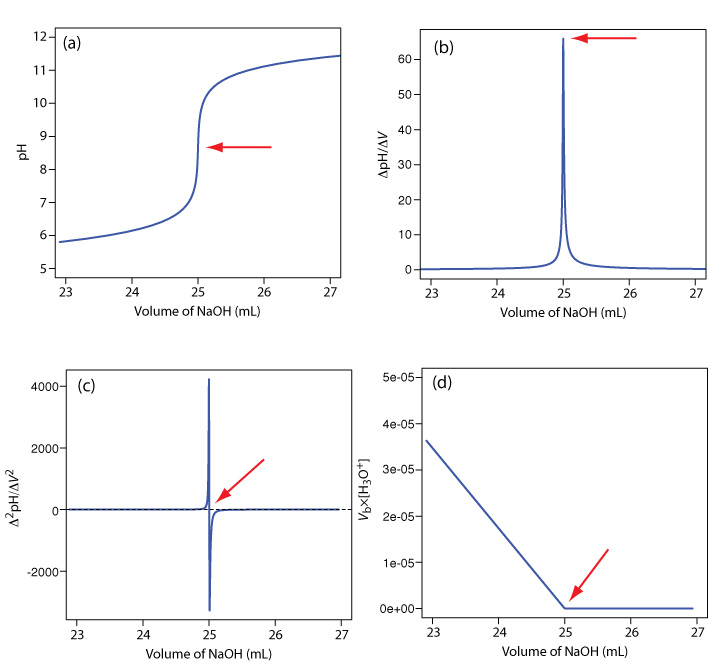
Figura 9.2.9 . Curvas de titulación para la titulación de 50.0 mL de 0.050 M CH 3 COOH con NaOH 0.10 M: (a) curva de titulación normal; (b) curva de titulación de primera derivada; (c) curva de titulación de segunda derivada; (d) Gran parcela. Las flechas rojas muestran la ubicación del punto final de cada titulación.
Otro método para ubicar el punto final es graficar la primera derivada de la curva de titulación, la cual da su pendiente en cada punto a lo largo del eje x. Examine la Figura 9.2.9 a y considere cómo cambia la pendiente de la curva de titulación a medida que nos acercamos, alcanzamos y pasamos el punto de equivalencia. Debido a que la pendiente alcanza su valor máximo en el punto de inflexión, la primera derivada muestra un pico en el punto de equivalencia (Figura 9.2.9 b). La segunda derivada de una curva de titulación puede ser más útil que la primera derivada porque el punto de equivalencia cruza el eje de volumen. La figura 9.2.9 c muestra la curva de titulación resultante.
Supongamos que tenemos los siguientes tres puntos en nuestra curva de valoración:
| volumen (mL) | pH |
| 23.65 | 6.00 |
| 23.91 | 6.10 |
| 24.13 | 6.20 |
Matemáticamente, podemos aproximar la primera derivada como\(\Delta \text{pH} / \Delta V\), donde\(\Delta \text{pH}\) está el cambio en el pH entre adiciones sucesivas de titulante. Usando los dos primeros puntos, la primera derivada es
\[\frac{\Delta \mathrm{pH}}{\Delta V}=\frac{6.10-6.00}{23.91-23.65}=0.385 \nonumber\]
que asignamos a la media de los dos volúmenes, o 23.78 mL. Para el segundo y tercer punto, la primera derivada es de 0.455 y el volumen promedio es de 24.02 mL.
| volumen (mL) | \(\Delta \text{pH}\) |
| 23.78 | 0.385 |
| 24.02 | 0.455 |
Podemos aproximar la segunda derivada como\(\Delta (\Delta \text{pH} / \Delta V) / \Delta V\), o\(\Delta^2 \text{pH} / \Delta V^2\). Usando los dos puntos de nuestro cálculo de la primera derivada, la segunda derivada es
\[\frac{\Delta^{2} \mathrm{p} \mathrm{H}}{\Delta V^{2}}=\frac{0.455-0.385}{24.02-23.78}=0.292 \nonumber\]
que asignamos al promedio de los dos volúmenes, o 23.90 mL. Tenga en cuenta que calcular la primera derivada viene a expensas de perder una pieza de información (tres puntos se convierten en dos puntos), y calcular la segunda derivada viene a expensas de perder dos piezas de información.
Los métodos derivados son particularmente útiles cuando se valora una muestra que contiene más de un analito. Si confiamos en indicadores para ubicar los puntos finales, entonces generalmente debemos completar titulaciones separadas para cada analito para que podamos ver el cambio de color para cada punto final. Sin embargo, si registramos la curva de titulación, entonces una sola titulación es suficiente. La precisión con la que podemos localizar el punto final también hace que los métodos derivados sean atractivos para un analito que tiene una curva de titulación normal poco definida.
Los métodos derivados funcionan bien solo si registramos datos suficientes durante el rápido aumento del pH cerca del punto de equivalencia. Esto generalmente no es un problema si utilizamos un valorador automático, como el visto anteriormente en la Figura 9.1.5. Debido a que el pH cambia tan rápidamente cerca del punto de equivalencia, un cambio de varias unidades de pH en un lapso de varias gotas de valorador no es inusual, la titulación manual no proporciona suficientes datos para una curva de titulación de derivados útil. Una valoración manual contiene abundancia de datos durante las porciones de la curva de titulación más suavemente ascendentes antes y después del punto de equivalencia. Estos datos también contienen información sobre el punto de equivalencia de la curva de titulación.
Consideremos nuevamente la titulación de ácido acético, CH 3 COOH, con NaOH. En cualquier momento durante la titulación, el ácido acético está en equilibrio con H 3 O + y CH 3 COO —
\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l )\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]
para lo cual la constante de equilibrio es
\[K_{a}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \nonumber\]
Antes del punto de equivalencia las concentraciones de CH 3 COOH y CH 3 COO — son
\[[\text{CH}_3\text{COOH}] = \frac {(\text{mol CH}_3\text{COOH})_\text{initial} - (\text{mol NaOH})_\text{added}} {\text{total volume}} = \frac {M_a V_a - M_b V_b} {V_a + V_b} \nonumber\]
\[[\text{CH}_3\text{COO}^-] = \frac {(\text{mol NaOH})_\text{added}} {\text{total volume}} = \frac {M_b V_b} {V_a + V_b} \nonumber\]
Sustituir estas ecuaciones en la expresión K a y reorganizar nos deja con
\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left(M_{b} V_{b}\right) /\left(V_{a}+V_{b}\right)}{\left\{M_{a} V_{a}-M_{b} V_{b}\right\} /\left(V_{a}+V_{b}\right)} \nonumber\]
\[K_{a} M_{a} V_{a}-K_{a} M_{b} V_{b}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left(M_{b} V_{b}\right) \nonumber\]
\[\frac{K_{a} M_{a} V_{a}}{M_{b}}-K_{a} V_{b}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] V_{b} \nonumber\]
Finalmente, reconociendo que el volumen del punto de equivalencia es
\[V_{eq}=\frac{M_{a} V_{a}}{M_{b}} \nonumber\]
nos deja con la siguiente ecuación.
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \times V_{b}=K_{\mathrm{a}} V_{eq}-K_{\mathrm{a}} V_{b} \nonumber\]
Para volúmenes de valorante antes del punto de equivalencia, una gráfica de\(V_b \times [\text{H}_3\text{O}^+]\) versus V b es una línea recta con una intercepción x de V eq y una pendiente de — K a. La figura 9.2.9 d muestra un resultado típico. Este método de análisis de datos, que convierte una porción de una curva de titulación en línea recta, es una gráfica Gran.
Los valores de K a determinados por este método pueden tener un error sustancial si se ignora el efecto de la actividad. Véase el Capítulo 6.9 para una discusión de la actividad.
Encontrar el punto final mediante el monitoreo de la temperatura
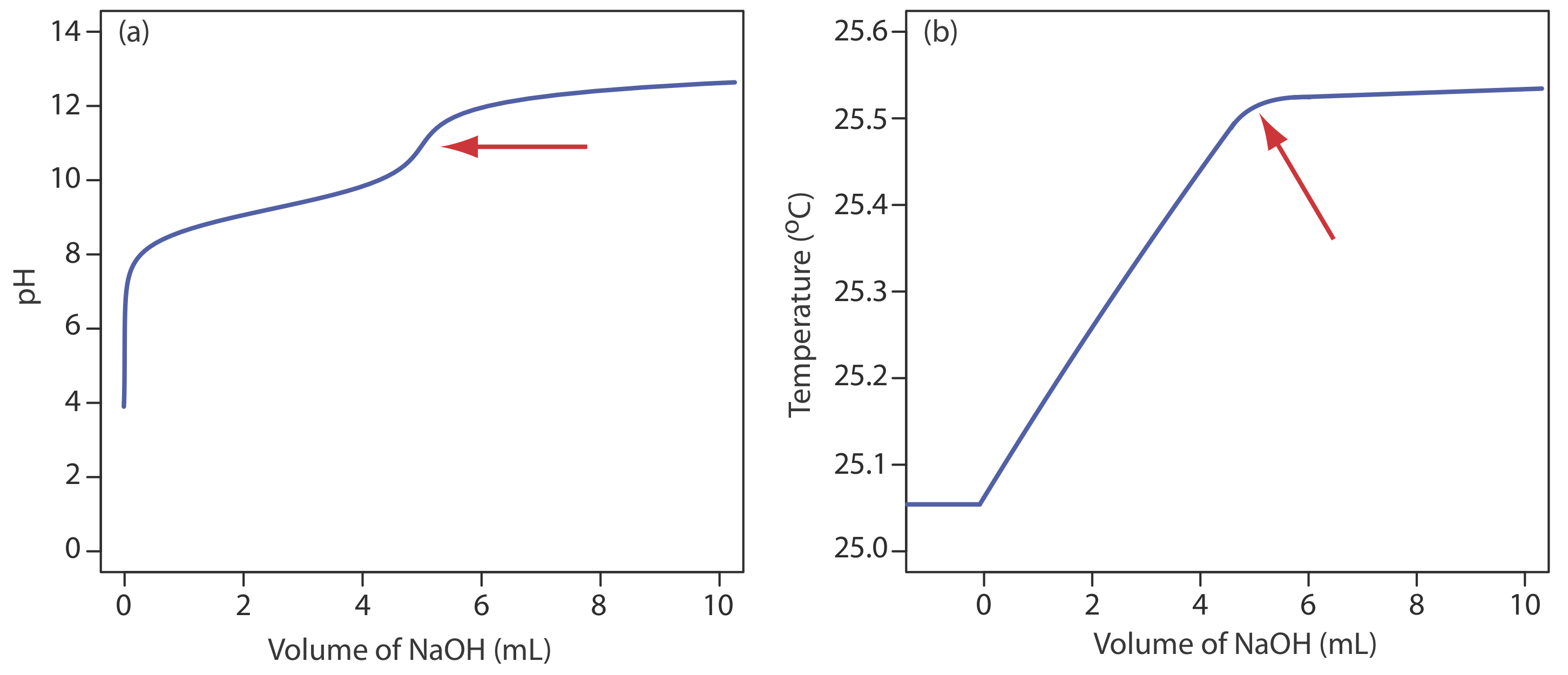
La reacción entre un ácido y una base es exotérmica. El calor generado por la reacción es absorbido por el titrand, lo que aumenta su temperatura. El monitoreo de la temperatura del titrand a medida que agregamos el valorante nos proporciona otro método para registrar una curva de titulación e identificar el punto final de la titulación (Figura 9.2.10 ).
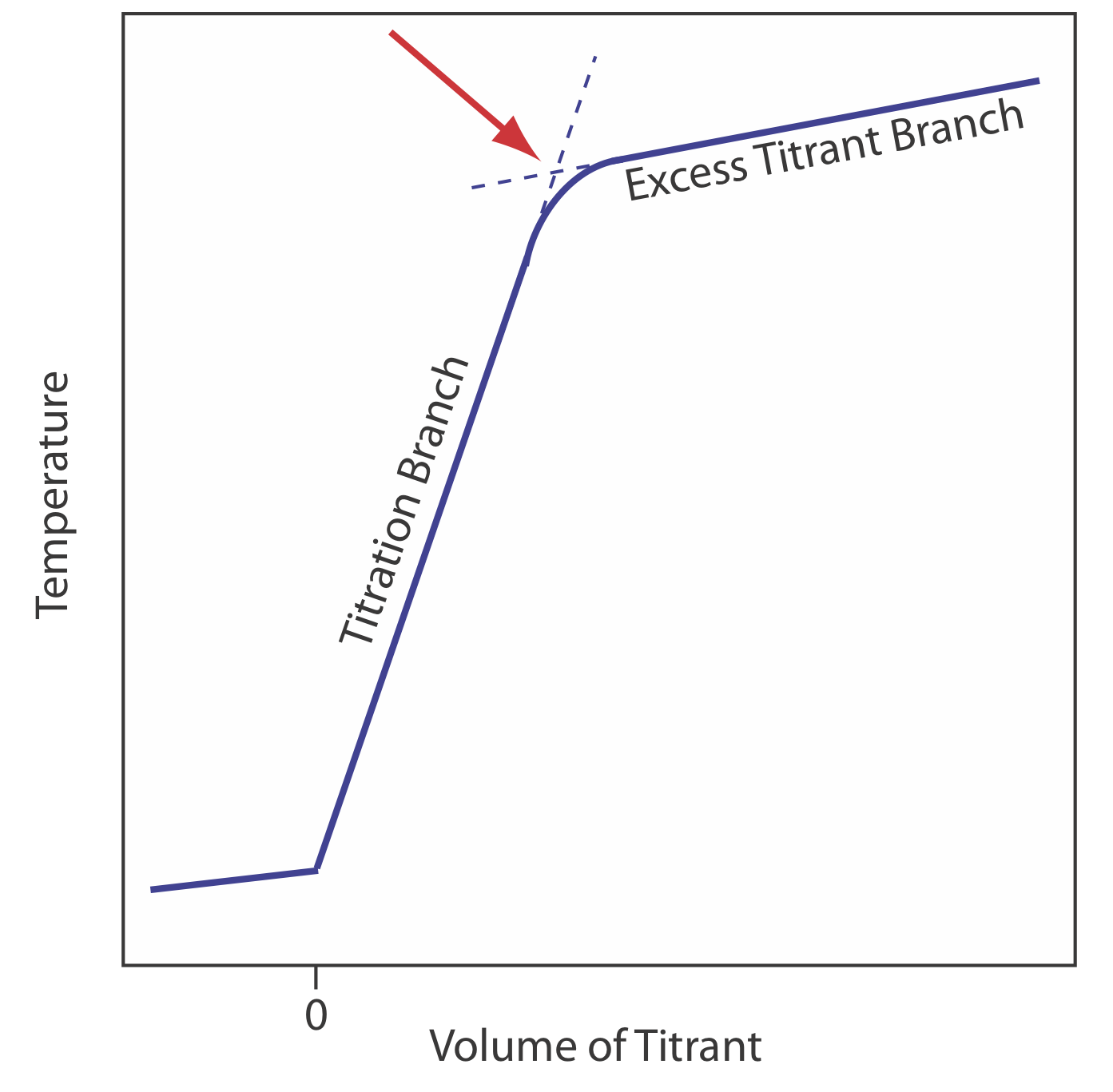
Antes de agregar el valorante, cualquier cambio en la temperatura de la titrand es el resultado del calentamiento o enfriamiento ya que se equilibra con el entorno. La adición de valorante inicia la reacción exotérmica ácido-base y aumenta la temperatura de la titrand. Esta parte de una curva de titulación termométrica se denomina rama de titulación. La temperatura continúa subiendo con cada adición de valorante hasta llegar al punto de equivalencia. Después del punto de equivalencia, cualquier cambio en la temperatura se debe a la entalpía de dilución del valorante y a la diferencia entre las temperaturas del valorante y el titrand. Idealmente, el punto de equivalencia es una intersección distinta de la rama de titulación y la rama de titulación en exceso. Como se muestra en la Figura 9.2.10 , sin embargo, una curva de titulación termométrica generalmente muestra curvatura cerca del punto de equivalencia debido a una reacción de neutralización incompleta o a la dilución excesiva del valorador y el valorante durante la titulación. Este último problema se minimiza mediante el uso de un valorante que es 10-100 veces más concentrado que el analito, aunque esto da como resultado un volumen de punto final muy pequeño y un error relativo mayor. Si es necesario, el punto final se encuentra por extrapolación.
Aunque no es un método común para monitorear una titulación ácido-base, una titulación termométrica tiene una clara ventaja sobre el monitoreo directo o indirecto del pH. Como se discutió anteriormente, el uso de un indicador o el monitoreo del pH está limitado por la magnitud de las constantes de equilibrio relevantes. Por ejemplo, la titulación del ácido bórico, H 3 BO 3, con NaOH no proporciona un punto final agudo al monitorear el pH porque el K a de ácido bórico\(5.8 \times 10^{-10}\) es demasiado pequeño (Figura 9.2.11 a). Debido a que la entalpía de neutralización del ácido bórico es bastante grande, —42.7 kJ/mol, su curva de titulación termométrica proporciona un punto final útil (Figura 9.2.11 b).
Titulaciones en Solventes No Acuosos
Hasta ahora hemos asumido que el valorante y el titrand son soluciones acuosas. Aunque el agua es el disolvente más común para la titrimetría ácido-base, cambiar a un disolvente no acuoso puede mejorar la viabilidad de una titulación.
Para un disolvente anfótero, SH, la constante de autoprotólisis, K s, relaciona la concentración de su forma protonada,\(\text{SH}_2^+\), a su forma desprotonada, S —
\[\begin{aligned} 2 \mathrm{SH} &\rightleftharpoons\mathrm{SH}_{2}^{+}+\mathrm{S}^{-} \\ K_{\mathrm{s}} &=\left[\mathrm{SH}_{2}^{+}\right][\mathrm{S}^-] \end{aligned} \nonumber\]
y el pH y el pOH del disolvente son
\[\begin{array}{l}{\mathrm{pH}=-\log \left[\mathrm{SH}_{2}^{+}\right]} \\ {\mathrm{pOH}=-\log \left[\mathrm{S}^{-}\right]}\end{array} \nonumber\]
Debe reconocer que K w es solo una forma específica de K s cuando el solvente es agua.
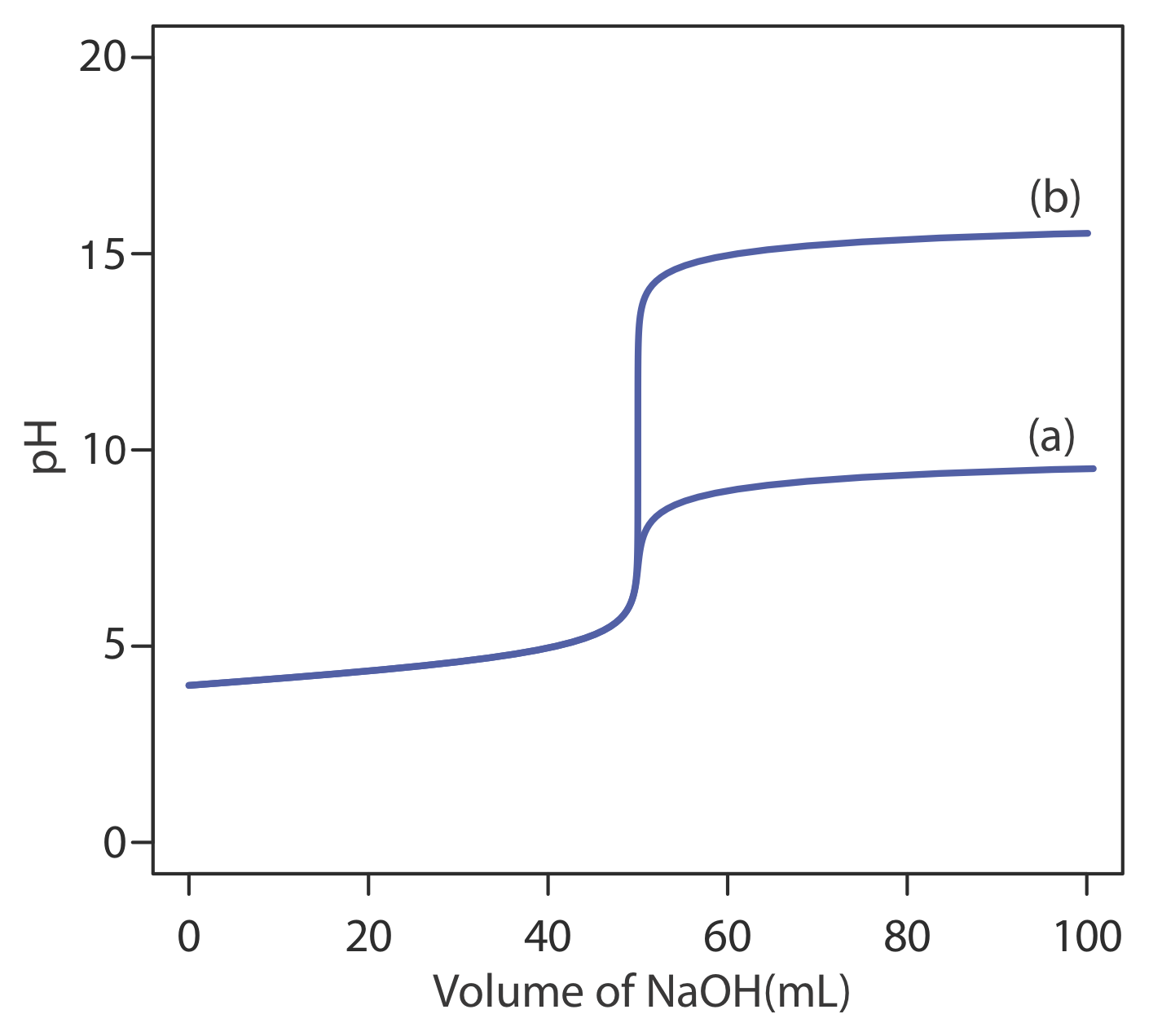
La limitación más importante que impone K s es el cambio en el pH durante una titulación. Para entender por qué esto es cierto, consideremos la titulación de 50.0 mL de HCl\(1.0 \times 10^{-4}\)\(1.0 \times 10^{-4}\) M usando NaOH M como valorante. Antes del punto de equivalencia, el pH es determinado por el ácido fuerte no titulado. Por ejemplo, cuando el volumen de NaOH es 90% de V eq, la concentración de H 3 O + es
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{M_{a} V_{a}-M_{b} V_{b}}{V_{a}+V_{b}} = \frac{\left(1.0 \times 10^{-4} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})-\left(1.0 \times 10^{-4} \ \mathrm{M}\right)(45.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+45.0 \ \mathrm{mL}} = 5.3 \times 10^{-6} \ \mathrm{M} \nonumber\]
y el pH es 5.3. Cuando el volumen de NaOH es 110% de V eq, la concentración de OH — es
\[\left[\mathrm{OH}^{-}\right]=\frac{M_{b} V_{b}-M_{a} V_{a}}{V_{a}+V_{b}} = \frac{\left(1.0 \times 10^{-4} \ \mathrm{M}\right)(55.0 \ \mathrm{mL})-\left(1.0 \times 10^{-4} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{55.0 \ \mathrm{mL}+50.0 \ \mathrm{mL}} = 4.8 \times 10^{-6} \ \mathrm{M} \nonumber\]
y el PoH es 5.3. El pH de la titrand es
\[\mathrm{pH}=\mathrm{p} K_{w}-\mathrm{pOH}=14.0-5.3=8.7 \nonumber\]
y el cambio en el pH de la titrand a medida que la titulación va de 90% a 110% de V eq es
\[\Delta \mathrm{pH}=8.7-5.3=3.4 \nonumber\]
Si realizamos la misma valoración en un disolvente anfiprótico no acuoso que tenga K s de\(1.0 \times 10^{-20}\), el pH después de agregar 45.0 mL de NaOH sigue siendo 5.3. Sin embargo, el pH después de agregar 55.0 mL de NaOH es
\[\mathrm{pH}=\mathrm{p} K_{s}-\mathrm{pOH}=20.0-5.3=14.7 \nonumber\]
En este caso el cambio en el pH
\[\Delta \mathrm{pH}=14.7-5.3=9.4 \nonumber\]
es significativamente mayor que la obtenida cuando la titulación se realiza en agua. La Figura 9.2.12 muestra las curvas de valoración tanto en los disolventes acuosos como en los no acuosos.
Otro parámetro que afecta la viabilidad de una titulación ácido-base es la constante de disociación de la titulación. Aquí, también, el solvente juega un papel importante. La fuerza de un ácido o una base es una medida relativa de lo fácil que es transferir un protón del ácido al disolvente o del disolvente a la base. Por ejemplo, HF, con una K a de\(6.8 \times 10^{-4}\), es mejor donante de protones que CH 3 COOH, para lo cual K a es\(1.75 \times 10^{-5}\).
El ácido más fuerte que puede existir en el agua es el ion hidronio, H 3 O +. HCl y HNO 3 son ácidos fuertes porque son mejores donantes de protones que H 3 O + y esencialmente donan todos sus protones a H 2 O, nivelando su fuerza ácida a la de H 3 O +. En un disolvente diferente HCl y HNO 3 pueden no comportarse como ácidos fuertes.
Si colocamos ácido acético en agua la reacción de disociación
\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}( l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]
no procede de manera significativa porque CH 3 COO — es una base más fuerte que H 2 O y H 3 O + es un ácido más fuerte que CH 3 COOH. Si colocamos el ácido acético en un disolvente que es una base más fuerte que el agua, como el amoníaco, entonces la reacción
\[\mathrm{CH}_{3} \mathrm{COOH}+\mathrm{NH}_{3}\rightleftharpoons\mathrm{NH}_{4}^{+}+\mathrm{CH}_{3} \mathrm{COO}^{-} \nonumber\]
procede en mayor medida. De hecho, tanto HCl como CH 3 COOH son ácidos fuertes en amoníaco.
Siendo iguales todas las demás cosas, la fuerza de un ácido débil aumenta si lo colocamos en un solvente que es más básico que el agua, y la fuerza de una base débil aumenta si lo colocamos en un solvente que es más ácido que el agua. En algunos casos, sin embargo, se observa el efecto contrario. Por ejemplo, el p K b para NH 3 es 4.75 en agua y es 6.40 en el ácido acético glacial más ácido. En contradicción con nuestras expectativas, el NH 3 es una base más débil en el disolvente más ácido. Una descripción completa del efecto del disolvente sobre la p K a del ácido débil o la p K b de una base débil está fuera del alcance de este texto. Debe tener en cuenta, sin embargo, que una titulación que no es factible en agua puede ser factible en un disolvente diferente.
Método Representativo 9.2.1: Determinación de Proteína en Pan
La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método típico de titulación ácido-base. Aunque cada método es único, la siguiente descripción de la determinación de proteína en el pan proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en el Método 13.86 publicado en Official Methods of Analysis, 8a Ed., Association of Official Agricultural Chemists: Washington, D. C., 1955.
Descripción de los métodos
Este método se basa en una determinación de% p/p de nitrógeno utilizando el método de Kjeldahl. La proteína en una muestra de pan se oxida a\(\text{NH}_4^+\) usar concentrado caliente H 2 SO 4. Después de hacer alcalina la solución, que se convierte\(\text{NH}_4^+\) en NH 3, el amoníaco se destila en un matraz que contiene una cantidad conocida de HCl. La cantidad de HCl sin reaccionar se determina mediante una retrotitulación usando un valorante estándar de base fuerte. Debido a que diferentes proteínas de cereales contienen cantidades similares de nitrógeno —en promedio hay 5.7 g de proteína por cada gramo de nitrógeno— multiplicamos el% w/w N determinado experimentalmente por un factor de 5.7 da el% w/w de proteína en la muestra.
Procedimiento
Transferir una muestra de pan de 2.0 g, previamente secada al aire y molida en polvo, a un matraz de digestión adecuado junto con 0.7 g de un catalizador de HgO, 10 g de K 2 SO 4 y 25 mL de H 2 SO 4 concentrado. Llevar la solución a ebullición. Continúe hirviendo hasta que la solución se vuelva transparente y luego hierva por al menos 30 minutos adicionales. Después de enfriar la solución por debajo de la temperatura ambiente, se retira el catalizador de Hg 2 + añadiendo 200 mL de H 2 O y 25 mL de 4% p/v K 2 S. Añadir unos gránulos de Zn para que sirvan como piedras de ebullición y 25 g de NaOH. Conecte rápidamente el matraz a un aparato de destilación y destile el NH 3 en un matraz colector que contenga una cantidad conocida de HCl estandarizado. La punta del condensador debe colocarse debajo de la superficie del ácido fuerte. Una vez completada la destilación, se valora el exceso de ácido fuerte con una solución estándar de NaOH usando rojo de metilo como indicador (Figura 9.2.13 ).
Preguntas
1. Oxidar la proteína convierte todo su nitrógeno en\(\text{NH}_4^+\). ¿Por qué no se determina la cantidad de nitrógeno valorando directamente el\(\text{NH}_4^+\) con una base fuerte?
Hay dos razones para no valorar directamente el ion amonio. Primero, debido a que\(\text{NH}_4^+\) es un ácido muy débil (su K a es\(5.6 \times 10^{-10}\)), su valoración con NaOH tiene un punto final mal definido. Segundo, aunque podamos determinar el punto final con exactitud y precisión aceptables, la solución también contiene una concentración sustancial de H 2 SO 4 sin reaccionar. La presencia de dos ácidos que difieren mucho en la concentración dificulta el análisis. Si la concentración del valorante es similar a la de H 2 SO 4, entonces el volumen del punto de equivalencia para la titulación de\(\text{NH}_4^+\) es demasiado pequeño para medirlo de manera confiable. Por otro lado, si la concentración del valorante es similar a la de\(\text{NH}_4^+\), el volumen necesario para neutralizar el H 2 SO 4 es irrazonablemente grande.
2. El amoníaco es un compuesto volátil como lo demuestra el fuerte olor de soluciones incluso diluidas. Esta volatilidad es una fuente potencial de error determinado. ¿Este error determinado es negativo o positivo?
Cualquier pérdida de NH 3 es pérdida de nitrógeno y, por lo tanto, una pérdida de proteína. El resultado es un error determinado negativo.
3. Identificar los pasos en este procedimiento que minimizan el error determinado a partir de la posible pérdida de NH 3.
Tres pasos específicos minimizan la pérdida de amoníaco: (1) la solución se enfría por debajo de la temperatura ambiente antes de agregar NaOH; (2) después de agregar NaOH, el matraz de digestión se conecta rápidamente al aparato de destilación; y (3) colocamos la punta del condensador debajo de la superficie del HCl para asegurar que el NH 3 reacciona con el HCl antes de que se pierda por volatilización.
4. ¿Cómo elimina K 2 S Hg 2 + y por qué es importante su eliminación?
La adición de sulfuro precipita Hg 2 + como HgS. Esto es importante porque NH 3 forma complejos estables con muchos iones metálicos, incluyendo Hg 2 +. Cualquier NH 3 que reaccione con Hg 2 + no se recoge durante la destilación, proporcionando otra fuente de error determinado.
Aplicaciones Cuantitativas
Aunque muchas aplicaciones cuantitativas de la titrimetría ácido-base han sido reemplazadas por otros métodos analíticos, algunas aplicaciones importantes continúan encontrando utilidad. En esta sección revisamos la aplicación general de la titrimetría ácido-base al análisis de compuestos inorgánicos y orgánicos, con énfasis en aplicaciones en análisis ambientales y clínicos. En primer lugar, sin embargo, se discute la selección y estandarización de titulantes ácidos y básicos.
Selección y estandarización de un valorante
Los titulantes ácidos fuertes más comunes son HCl, HClO 4 y H 2 SO 4. Las soluciones de estos titulantes generalmente se preparan diluyendo una solución madre concentrada disponible comercialmente. Debido a que la concentración de un ácido concentrado se conoce solo aproximadamente, la concentración del valorante se determina estandarizando contra una de las bases débiles estándar primarias enumeradas en la Tabla 9.2.4 .
Las concentraciones nominales de las soluciones madre concentradas son 12.1 M HCl, 11.7 M HClO 4 y 18.0 M H 2 SO 4. Las concentraciones reales de estos ácidos se dan como %p/v y varían ligeramente de lote a lote.
El valorante de base fuerte más común es el NaOH, el cual está disponible tanto como un sólido impuro como como una solución de aproximadamente 50% p/v. Las soluciones de NaOH se estandarizan contra cualquiera de los estándares primarios de ácido débil enumerados en la Tabla\(\PageIndex[4|\).
El uso de NaOH como valorante se complica por la contaminación potencial de la siguiente reacción entre CO 2 disuelto y OH —.
Cualquier solución en contacto con la atmósfera contiene una pequeña cantidad de CO 2 (ac) del equilibrio
\[\mathrm{CO}_{2}(g)\rightleftharpoons\mathrm{CO}_{2}(a q) \nonumber\]
Durante la titulación, el NaOH reacciona tanto con la titulación como con CO 2, lo que aumenta el volumen de NaOH necesario para alcanzar el punto final de la titulación. Esto no es un problema si el pH del punto final es inferior a 6. Por debajo de este pH el\(\text{CO}_3^{2-}\) de la reacción\ ref {9.7} reacciona con H 3 O + para formar ácido carbónico.
Combinando reacción\ ref {9.7} y reacción\ ref {9.8} da una reacción global que no incluye OH —.
\[\mathrm{CO}_{2}(a q)+\mathrm{H}_{2} \mathrm{O}(l ) \longrightarrow \mathrm{H}_{2} \mathrm{CO}_{3}(a q) \nonumber\]
En estas condiciones la presencia de CO 2 no afecta la cantidad de OH — utilizada en la titulación y no es una fuente de error determinado.
Si el pH del punto final está entre 6 y 10, sin embargo, la neutralización de\(\text{CO}_3^{2-}\) requiere un protón
\[\mathrm{CO}_{3}^{2-}(a q)+\mathrm{H}_{3} \mathrm{O}^{+}(a q) \rightarrow \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{HCO}_{3}^{-}(a q) \nonumber\]
y la reacción neta entre CO 2 y OH — es
\[\mathrm{CO}_{2}(a q)+\mathrm{OH}^{-}(a q) \rightarrow \mathrm{HCO}_{3}^{-}(a q) \nonumber\]
Bajo estas condiciones algo de OH — se consume en la neutralización de CO 2, lo que resulta en un determinado error. Podemos evitar el error determinado si utilizamos el mismo pH de punto final tanto para la estandarización de NaOH como para el análisis de nuestro analito, aunque esto no siempre es práctico.
El NaOH sólido siempre está contaminado con carbonato debido a su contacto con la atmósfera, y no podemos usarlo para preparar una solución de NaOH libre de carbonato. Las soluciones de NaOH libre de carbonato se preparan a partir de NaOH al 50% p/v porque el Na 2 CO 3 es insoluble en NaOH concentrado. Cuando se absorbe CO 2, el Na 2 CO 3 precipita y se asienta en el fondo del recipiente, lo que permite el acceso al NaOH libre de carbonato. Al prepelar una solución de NaOH, asegúrese de usar agua que esté libre de CO 2 disuelto. Brevemente hirviendo el agua expulsa CO 2; después de que se enfríe, el agua se emplea para preparar soluciones libres de carbonato de NaOH. Una solución de NaOH libre de carbonato es relativamente estable si limitamos su contacto con la atmósfera. Las soluciones estándar de hidróxido de sodio no se almacenan en botellas de vidrio ya que el NaOH reacciona con el vidrio para formar silicato; en su lugar, almacenar dichas soluciones en botellas de polietileno.
Análisis Inorgánico
La titrimetría ácido-base es un método estándar para el análisis cuantitativo de muchos ácidos y bases inorgánicos. Se utiliza una solución estándar de NaOH para determinar la concentración de ácidos inorgánicos, como H 3 PO 4 o H 3 AsO 4, y bases inorgánicas, como Na 2 CO 3 se analizan usando una solución estándar de HCl.
Si se trata de un ácido inorgánico o una base demasiado débil para ser analizada por una titulación ácido-base acuosa, es posible completar el análisis ajustando el disolvente o mediante un análisis indirecto. Por ejemplo, al analizar ácido bórico, H 3 BO 3, mediante titulación con NaOH, la precisión está limitada por la pequeña constante de disociación ácida del ácido bórico de\(5.8 \times 10^{-10}\). El valor de K a del ácido bórico aumenta\(1.5 \times 10^{-4}\) en presencia de manitol, ya que forma un complejo estable con el ion borato, lo que resulta en un punto final más nítido y una valoración más precisa. Del mismo modo, el análisis de sales de amonio está limitado por la pequeña constante de disociación ácida del ion amonio de\(5.7 \times 10^{-10}\). Podemos determinar\(\text{NH}_4^+\) indirectamente mediante el uso de una base fuerte para convertirlo en NH 3, el cual se retira por destilación y se titula con HCl. Debido a que\(\text{NH}_4^+\) NH 3 es una base débil más fuerte que un ácido débil (su K b es\(1.58 \times 10^{-5}\)), la titulación tiene un punto final más agudo.
Podemos analizar un analito inorgánico neutro si primero podemos convertirlo en un ácido o una base. Por ejemplo, podemos determinar la concentración de\(\text{NO}_3^-\) reduciéndola a NH 3 en una solución fuertemente alcalina usando la aleación de Devarda, una mezcla de 50% p/p de Cu, 45% p/p Al y 5% p/p de Zn.
\[3 \mathrm{NO}_{3}^{-}(a q)+8 \mathrm{Al}(s)+5 \mathrm{OH}^{-}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l) \rightarrow 8 \mathrm{AlO}_{2}^{-}(a q)+3 \mathrm{NH}_{3}(a q) \nonumber\]
El NH 3 se retira por destilación y se titula con HCl. Alternativamente, podemos valorar\(\text{NO}_3^-\) como una base débil colocándola en un disolvente ácido no acuoso, como ácido acético anhidro, y usando HClO 4 como valorante.
La titrimetría ácido-base continúa siendo catalogada como método estándar para la determinación de alcalinidad, acidez y CO 2 libre en aguas y aguas residuales. La alcalinidad es una medida de la capacidad de una muestra para neutralizar ácidos. Las fuentes más importantes de alcalinidad son OH —\(\text{HCO}_3^-\), y\(\text{CO}_3^{2-}\), aunque otras bases débiles, como el fosfato, pueden contribuir a la alcalinidad general. La alcalinidad total se determina valorando a un pH de punto final fijo de 4.5 (o al punto final verde de bromocresol) usando una solución estándar de HCl o H 2 SO 4. Los resultados se reportan como mg CaCo 3 /L.
Aunque una variedad de bases fuertes y bases débiles pueden contribuir a la alcalinidad de una muestra, una sola titulación no puede distinguir entre las posibles fuentes. El reporte de la alcalinidad total como si CaCo 3 fuera la única fuente proporciona un medio para comparar las capacidades de neutralización ácida de diferentes muestras.
Cuando las fuentes de alcalinidad se limitan a OH —, y\(\text{HCO}_3^-\)\(\text{CO}_3^{2-}\), titulaciones separadas a un pH de 4.5 (o el punto final verde de bromocresol) y un pH de 8.3 (o el punto final de fenolftaleína) nos permiten determinar qué especies están presentes y sus respectivas concentraciones. Las curvas de valoración para OH —\(\text{HCO}_3^-\), y se\(\text{CO}_3^{2-}\) muestran en la Figura 9.2.14 . Para una solución que contiene OH — alcalinidad solamente, el volumen de ácido fuerte necesario para alcanzar cada uno de los dos puntos finales es idéntico (Figura 9.2.14 a). Cuando la única fuente de alcalinidad es\(\text{CO}_3^{2-}\), el volumen de ácido fuerte necesario para alcanzar el punto final a un pH de 4.5 es exactamente el doble del necesario para alcanzar el punto final a un pH de 8.3 (Figura 9.2.14 b). Si una solución contiene solo\(\text{HCO}_3^-\) alcalinidad, el volumen de ácido fuerte necesario para alcanzar el punto final a un pH de 8.3 es cero, pero que para el punto final de pH 4.5 es mayor que cero (Figura 9.2.14 c).
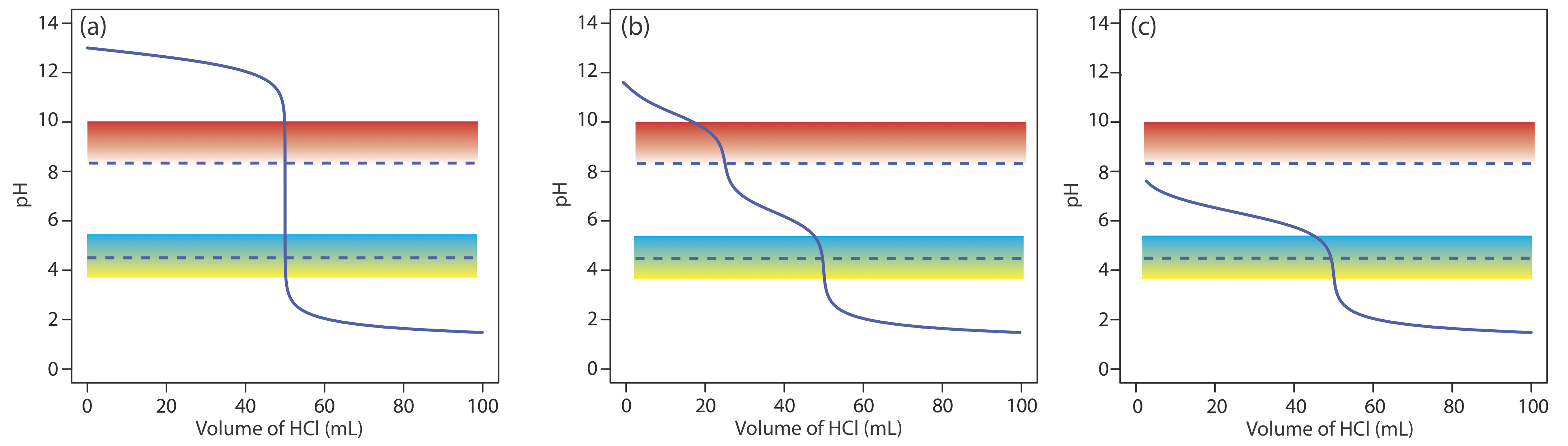
Una mezcla de OH — y\(\text{CO}_3^{2-}\) o una mezcla de\(\text{HCO}_3^-\) y\(\text{CO}_3^{2-}\) también es posible. Consideremos, por ejemplo, una mezcla de OH — y\(\text{CO}_3^{2-}\). El volumen de ácido fuerte para valorar OH — es el mismo si valoramos a un pH de 8.3 o a un pH de 4.5. La titulación\(\text{CO}_3^{2-}\) a un pH de 4.5, sin embargo, requiere el doble de ácido fuerte que la titulación a un pH de 8.3. En consecuencia, cuando valoramos una mezcla de estos dos iones, el volumen de ácido fuerte necesario para alcanzar un pH de 4.5 es menor al doble del necesario para alcanzar un pH de 8.3. Para una mezcla de\(\text{HCO}_3^-\) y\(\text{CO}_3^{2-}\) el volumen de ácido fuerte necesario para alcanzar un pH de 4.5 es más del doble del necesario para alcanzar un pH de 8.3. El cuadro 9.2.5 resume la relación entre las fuentes de alcalinidad y los volúmenes de titulante necesarios para alcanzar los dos puntos finales.
Una mezcla de OH — y\(\text{HCO}_3^-\) es inestable con respecto a la formación de\(\text{CO}_3^{2-}\). El problema 15 en los problemas de fin de capítulo te pide que expliques por qué esto es cierto.
La acidez es una medida de la capacidad de una muestra de agua para neutralizar la base y se divide en ácido fuerte y acidez ácida débil. La fuerte acidez ácida de ácidos inorgánicos como HCl, HNO 3 y H 2 SO 4 es común en efluentes industriales y en el drenaje ácido de minas. La acidez ácida débil generalmente está dominada por la formación de H 2 CO 3 a partir de CO 2 disuelto, pero también incluye contribuciones de iones metálicos hidrolizables como Fe 3 +, Al 3+ y Mn 2 +. Además, la acidez ácida débil puede incluir un aporte de ácidos orgánicos.
La acidez se determina valorando con una solución estándar de NaOH a un pH fijo de 3.7 (o el punto final azul de bromotimol) y a un pH fijo de 8.3 (o el punto final de fenolftaleína). La titulación a un pH de 3.7 proporciona una medida de acidez ácida fuerte, y la titulación a un pH de 8.3 proporciona una medida de la acidez total. La acidez ácida débil es la diferencia entre la acidez total y la acidez ácida fuerte. Los resultados se expresan como la cantidad de CaCo 3 que puede ser neutralizada por la acidez de la muestra. Un enfoque alternativo para determinar acidez fuerte y acidez ácida débil es obtener una curva de titulación potenciométrica y usar una gráfica Gran para determinar los dos puntos de equivalencia. Este enfoque se ha utilizado, por ejemplo, para determinar las formas de acidez en los aerosoles atmosféricos [Ferek, R. J.; Lazrus, A. L.; Haagenson, P. L.; Winchester, J. W. Environ. Sci. Tecnol. 1983, 17, 315—324].
Como es el caso de la alcalinidad, la acidez se reporta como mg CaCo 3 /L.
El agua en contacto ya sea con la atmósfera o con sedimentos que contienen carbonato contiene CO libre 2 en equilibrio con CO 2 (g) y con H acuoso 2 CO 3,\(\text{HCO}_3^-\) y\(\text{CO}_3^{2-}\). La concentración de CO 2 libre se determina valorando con una solución estándar de NaOH al punto final de fenolftaleína, o a un pH de 8.3, con resultados reportados como mg de CO 2/L. Este análisis es esencialmente el mismo que para la determinación de la acidez total y se utiliza únicamente para muestras de agua que no contengan acidez ácida fuerte.
El CO 2 libre es lo mismo que el CO 2 (aq).
Análisis Orgánico
La titrimetría ácido-base sigue teniendo un papel pequeño pero importante para el análisis de compuestos orgánicos en laboratorios farmacéuticos, bioquímicos, agrícolas y ambientales. Quizás la valoración ácido-base más empleada es el análisis de Kjeldahl para nitrógeno orgánico. Ejemplos de analitos determinados por un análisis de Kjeldahl incluyen cafeína y sacarina en productos farmacéuticos, proteínas en alimentos y el análisis de nitrógeno en fertilizantes, lodos y sedimentos. Cualquier nitrógeno presente en un estado de oxidación —3 se oxida cuantitativamente a\(\text{NH}_4^+\). Debido a que algunos compuestos heterocíclicos aromáticos, como la piridina, son difíciles de oxidar, se utiliza un catalizador para asegurar una oxidación cuantitativa. El nitrógeno en otros estados de oxidación, como nitrógenos nitro y azo, se oxidan a N 2, lo que da como resultado un error determinado negativo. Incluyendo un agente reductor, como el ácido salicílico, convierte este nitrógeno a un estado de oxidación —3, eliminando esta fuente de error. La Tabla 9.2.6 proporciona ejemplos adicionales en los que un elemento se convierte cuantitativamente en un ácido o base valorable.
Varios grupos funcionales orgánicos son ácidos débiles o bases débiles. Los grupos funcionales carboxílicos (—COOH), sulfónicos (—SO 3 H) y fenólicos (—C 6 H 5 OH) son ácidos débiles que se titulan exitosamente en solventes acuosos o no acuosos. El hidróxido de sodio es el valorante de elección para soluciones acuosas. Las titulaciones no acuosas a menudo se llevan a cabo en un disolvente básico, como la etilendiamina, utilizando hidróxido de tetrabutilamónico, (C 4 H 9) 4 NOH, como valorante. Las aminas alifáticas y aromáticas son bases débiles que se valoran usando HCl en soluciones acuosas, o HClO 4 en ácido acético glacial. Otros grupos funcionales se analizan indirectamente después de una reacción que produce o consume un ácido o una base. Los ejemplos típicos se muestran en la Tabla 9.2.7 .
Muchos compuestos farmacéuticos son ácidos débiles o bases débiles que se analizan mediante una titulación de ácido-base acuosa o no acuosa; los ejemplos incluyen ácido salicílico, fenobarbital, cafeína y sulfanilamida. Los aminoácidos y proteínas se analizan en ácido acético glacial usando HClO 4 como valorante. Por ejemplo, un procedimiento para determinar la cantidad de proteína disponible nutricionalmente utiliza una titulación ácido-base de residuos de lisina [(a) Molnár-Perl, I.; Pintée-Szakács, M. Anal. Chim. Acta 1987, 202, 159—166; b) Barbosa, J.; Bosch, E.; Cortina, J. L.; Rosés, M. Anal. Chim. Acta 1992, 256, 177—181].
Cálculos cuantitativos
La relación cuantitativa entre el valorador y el valorante está determinada por la estequiometría de la reacción de titulación. Si el titrand es poliprótico, entonces debemos saber a qué punto de equivalencia estamos titulando. El siguiente ejemplo ilustra cómo podemos usar un diagrama de escalera para determinar la estequiometría de una reacción de titulación.
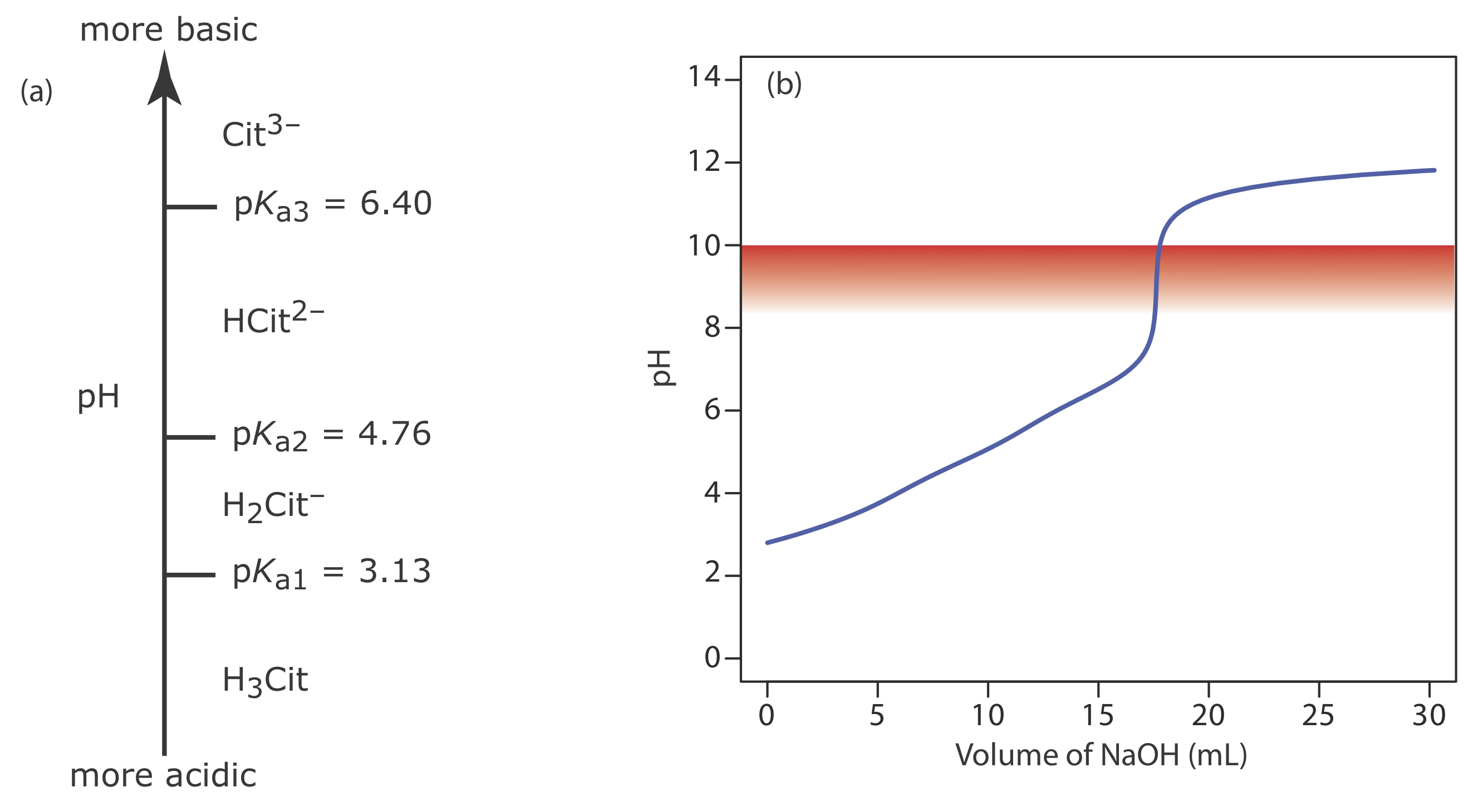
Una muestra de 50.00-mL de una bebida cítrica requiere 17.62 mL de NaOH 0.04166 M para alcanzar el punto final de fenolftaleína. Expresar la acidez de la muestra en gramos de ácido cítrico, C 6 H 8 O 7, por 100 mL.
Solución
Debido a que el ácido cítrico es un ácido triprótico débil, primero debemos determinar si el punto final de fenolftaleína corresponde al primer, segundo o tercer punto de equivalencia. El diagrama de escalera de ácido cítrico se muestra en la Figura {{template.index (ID:15)} a. Con base en este diagrama de escalera, el primer punto de equivalencia se encuentra entre un pH de 3.13 y un pH de 4.76, el segundo punto de equivalencia está entre un pH de 4.76 y un pH de 6.40, y el tercer punto de equivalencia es mayor que un pH de 6.40. Debido a que el pH del punto final de la fenolftaleína es 8.3—10.0 (ver Tabla {{Template.index (ID:3)}}), la titulación debe proceder al tercer punto de equivalencia y la reacción de titulación es
\[ \mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{7}(a q)+3 \mathrm{OH}^{-}(a q) \longrightarrow \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}_{7}^{3-}(a q)+3 \mathrm{H}_{2} \mathrm{O}(l) \nonumber\]
Para alcanzar el punto de equivalencia, cada mol de ácido cítrico consume tres moles de NaOH; así
\[(0.04166 \ \mathrm{M} \ \mathrm{NaOH})(0.01762 \ \mathrm{L} \ \mathrm{NaOH})=7.3405 \times 10^{-4} \ \mathrm{mol} \ \mathrm{NaOH} \nonumber\]
\[7.3405 \times 10^{-4} \ \mathrm{mol} \ \mathrm{NaOH} \times \frac{1 \ \mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{7}}{3 \ \mathrm{mol} \ \mathrm{NaOH}}= 2.4468 \times 10^{-4} \ \mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{7} \nonumber\]
\[2.4468 \times 10^{-4} \ \mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{7} \times \frac{192.1 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{7}}{\mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{7}}=0.04700 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{8} \mathrm{O}_{7} \nonumber\]
Debido a que esta es la cantidad de ácido cítrico en una muestra de 50.00 mL, la concentración de ácido cítrico en la bebida cítrica es de 0.09400 g/100 mL. La curva de titulación completa se muestra en la Figura 9.2.15 b.
Su empresa recibió recientemente un envío de ácido salicílico, C 7 H 6 O 3, para su uso en la producción de ácido acetilsalicílico (aspirina). Puedes aceptar el envío solo si el ácido salicílico es más del 99% puro. Para evaluar la pureza del envío, se disuelve una muestra de 0.4208-g en agua y se valora hasta el punto final de fenolftaleína, utilizando 21.92 mL de NaOH 0.1354 M. Reporte la pureza del envío como %w/w C 7 H 6 O 3. El ácido salicílico es un ácido diprótico débil con valores p K a de 2.97 y 13.74.
- Responder
-
Debido a que el ácido salicílico es un ácido diprótico débil, primero debemos determinar a qué punto de equivalencia se está titulando. Utilizando como guía los valores p K a de ácido salicílico, el pH en el primer punto de equivalencia se encuentra entre 2.97 y 13.74, y los segundos puntos de equivalencia se encuentran a un pH mayor a 13.74. De la Tabla 9.2.3 , el punto final de la fenolftaleína está en el rango de pH 8.3—10.0. La titulación, por lo tanto, es hasta el primer punto de equivalencia para el cual los moles de NaOH son iguales a los moles de ácido salicílico; así
\[(0.1354 \ \mathrm{M})(0.02192 \ \mathrm{L})=2.968 \times 10^{-3} \ \mathrm{mol} \ \mathrm{NaOH} \nonumber\]
\[2.968 \times 10^{-3} \ \mathrm{mol} \ \mathrm{NaOH} \times \frac{1 \ \mathrm{mol} \ \mathrm{C}_{7} \mathrm{H}_{6} \mathrm{O}_{3}}{\mathrm{mol} \ \mathrm{NaOH}} \times \frac{138.12 \ \mathrm{g} \ \mathrm{C}_{7} \mathrm{H}_{6} \mathrm{O}_{3}}{\mathrm{mol} \ \mathrm{C}_{7} \mathrm{H}_{6} \mathrm{O}_{3}}=0.4099 \ \mathrm{g} \ \mathrm{C}_{7} \mathrm{H}_{6} \mathrm{O}_{3} \nonumber\]
\[\frac{0.4099 \ \mathrm{g} \ \mathrm{C}_{7} \mathrm{H}_{6} \mathrm{O}_{3}}{0.4208 \ \mathrm{g} \text { sample }} \times 100=97.41 \ \% \mathrm{w} / \mathrm{w} \ \mathrm{C}_{7} \mathrm{H}_{6} \mathrm{O}_{3} \nonumber\]
Debido a que la pureza de la muestra es inferior al 99%, rechazamos el envío.
En un análisis indirecto el analito participa en una o más reacciones preliminares, una de las cuales produce o consume ácido o base. A pesar de la complejidad adicional, los cálculos son sencillos.
La pureza de una preparación farmacéutica de sulfanilamida, C 6 H 4 N 2 O 2 S, se determina oxidando el azufre a SO 2 y burbujeándolo a través de H 2 O 2 para producir H 2 SO 4. El ácido se valora hasta el punto final de azul de bromotimol usando una solución estándar de NaOH. Calcular la pureza de la preparación dado que una muestra de 0.5136 g requiere 48.13 mL de NaOH 0.1251 M.
Solución
El punto final del azul de bromotimol tiene un rango de pH de 6.0—7.6. El ácido sulfúrico es un ácido diprótico, con un p K a2 de 1.99 (el primer valor K a es muy grande y la reacción de disociación ácida va a completarse, razón por la cual H 2 SO4 es un ácido fuerte). La titulación, por lo tanto, procede al segundo punto de equivalencia y la reacción de titulación es
\[\mathrm{H}_{2} \mathrm{SO}_{4}(a q)+2 \mathrm{OH}^{-}(a q) \longrightarrow 2 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{SO}_{4}^{2-}(a q) \nonumber\]
Usando los resultados de la titulación, hay
\[(0.1251 \ \mathrm{M} \ \mathrm{NaOH})(0.04813 \ \mathrm{L} \ \mathrm{NaOH})=6.021 \times 10^{-3} \ \mathrm{mol} \ \mathrm{NaOH} \nonumber\]
\[6.012 \times 10^{-3} \text{ mol NaOH} \times \frac{1 \text{ mol} \mathrm{H}_{2} \mathrm{SO}_{4}} {2 \text{ mol NaOH}} = 3.010 \times 10^{-3} \text{ mol} \mathrm{H}_{2} \mathrm{SO}_{4} \nonumber\]
\[3.010 \times 10^{-3} \ \mathrm{mol} \ \mathrm{H}_{2} \mathrm{SO}_{4} \times \frac{1 \ \mathrm{mol} \text{ S}}{\mathrm{mol} \ \mathrm{H}_{2} \mathrm{SO}_{4}} \times \ \frac{1 \ \mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{4} \mathrm{N}_{2} \mathrm{O}_{2} \mathrm{S}}{\mathrm{mol} \text{ S}} \times \frac{168.17 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{4} \mathrm{N}_{2} \mathrm{O}_{2} \mathrm{S}}{\mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{4} \mathrm{N}_{2} \mathrm{O}_{2} \mathrm{S}}= 0.5062 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{4} \mathrm{N}_{2} \mathrm{O}_{2} \mathrm{S} \nonumber\]
producido cuando el SO 2 se burbujea a través de H 2 O 2. Debido a que todo el azufre en H 2 SO 4 proviene de la sulfanilamida, podemos usar una conservación de masa para determinar la cantidad de sulfanilamida en la muestra.
\[\frac{0.5062 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{4} \mathrm{N}_{2} \mathrm{O}_{2} \mathrm{S}}{0.5136 \ \mathrm{g} \text { sample }} \times 100=98.56 \ \% \mathrm{w} / \mathrm{w} \ \mathrm{C}_{6} \mathrm{H}_{4} \mathrm{N}_{2} \mathrm{O}_{2} \mathrm{S} \nonumber\]
La concentración de NO 2 en el aire se determina haciendo pasar la muestra a través de una solución de H 2 O 2, que oxida NO 2 a HNO 3, y titulando el HNO 3 con NaOH. Cuál es la concentración de NO 2, en mg/L, si una muestra de aire de 5.0 L requiere 9.14 mL de NaOH 0.01012 M para alcanzar el punto final del rojo de metilo
- Responder
-
Los moles de HNO 3 producidos al tirar de la muestra a través de H 2 O 2 son
\[(0.01012 \ \mathrm{M})(0.00914 \ \mathrm{L}) \times \frac{1 \ \mathrm{mol} \ \mathrm{HNO}_{3}}{\mathrm{mol} \ \mathrm{NaOH}}=9.25 \times 10^{-5} \ \mathrm{mol} \ \mathrm{HNO}_{3} \nonumber\]
Una conservación de la masa sobre nitrógeno requiere que cada mol de NO 2 produzca un mol de HNO 3; así, la masa de NO 2 en la muestra es
\[9.25 \times 10^{-5} \ \mathrm{mol} \ \mathrm{HNO}_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{NO}_{2}}{\mathrm{mol} \ \mathrm{HNO}_{3}} \times \frac{46.01 \ \mathrm{g} \ \mathrm{NO}_{2}}{\mathrm{mol} \ \mathrm{NO}_{2}}=4.26 \times 10^{-3} \ \mathrm{g} \ \mathrm{NO}_{2} \nonumber\]
y la concentración de NO 2 es
\[\frac{4.26 \times 10^{-3} \ \mathrm{g} \ \mathrm{NO}_{2}}{5 \ \mathrm{L} \text { air }} \times \frac{1000 \ \mathrm{mg}}{\mathrm{g}}=0.852 \ \mathrm{mg} \ \mathrm{NO}_{2} \ \mathrm{L} \text { air } \nonumber\]
Para una valoración posterior debemos considerar dos reacciones ácido-base. Nuevamente, los cálculos son sencillos.
La cantidad de proteína en una muestra de queso se determina mediante un análisis de Kjeldahl para nitrógeno. Después de digerir una muestra de queso de 0.9814-g, el nitrógeno se oxida\(\text{NH}_4^+\), se convierte en NH 3 con NaOH, y el NH 3 se destila en un matraz de recolección que contiene 50.00 mL de HCl 0.1047 M. El exceso de HCl se vuelve a valorar con NaOH 0.1183 M, requiriendo 22.84 mL para alcanzar el punto final del azul de bromotimol. Reporte el% w/w de proteína en el queso asumiendo que hay 6.38 gramos de proteína por cada gramo de nitrógeno en la mayoría de los productos lácteos.
Solución
El HCl en el matraz de recolección reacciona con dos bases
\[\mathrm{HCl}(a q)+\mathrm{NH}_{3}(a q) \rightarrow \mathrm{NH}_{4}^{+}(a q)+\mathrm{Cl}^{-}(a q) \nonumber\]
\[\mathrm{HCl}(a q)+\mathrm{OH}^{-}(a q) \rightarrow \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{Cl}^{-}(a q) \nonumber\]
El frasco de colección contiene originalmente
\[(0.1047 \ \mathrm{M \ HCl})(0.05000 \ \mathrm{L \ HCl})=5.235 \times 10^{-3} \mathrm{mol} \ \mathrm{HCl} \nonumber\]
de los cuales
\[(0.1183 \ \mathrm{M} \ \mathrm{NaOH})(0.02284 \ \mathrm{L} \ \mathrm{NaOH}) \times \frac{1 \ \mathrm{mol} \ \mathrm{HCl}}{\mathrm{mol} \ \mathrm{NaOH}}=2.702 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} \nonumber\]
reaccionar con NaOH. La diferencia entre los moles totales de HCl y los moles de HCl que reaccionan con NaOH son los moles de HCl que reaccionan con NH 3.
\[5.235 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl}-2.702 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} =2.533 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} \nonumber\]
Debido a que todo el nitrógeno en NH 3 proviene de la muestra de queso, utilizamos una conservación de masa para determinar los gramos de nitrógeno en la muestra.
\[2.533 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} \times \frac{1 \ \mathrm{mol} \ \mathrm{NH}_{3}}{\mathrm{mol} \ \mathrm{HCl}} \times \frac{14.01 \ \mathrm{g} \ \mathrm{N}}{\mathrm{mol} \ \mathrm{NH}_{3}}=0.03549 \ \mathrm{g} \ \mathrm{N} \nonumber\]
La masa de proteína, por lo tanto, es
\[0.03549 \ \mathrm{g} \ \mathrm{N} \times \frac{6.38 \ \mathrm{g} \text { protein }}{\mathrm{g} \ \mathrm{N}}=0.2264 \ \mathrm{g} \text { protein } \nonumber\]
y el% p/p de proteína es
\[\frac{0.2264 \ \mathrm{g} \text { protein }}{0.9814 \ \mathrm{g} \text { sample }} \times 100=23.1 \ \% \mathrm{w} / \mathrm{w} \text { protein } \nonumber\]
La piedra caliza consiste principalmente en CaCo 3, con trazas de óxidos de hierro y otros óxidos metálicos. Para determinar la pureza de una piedra caliza, se disuelve una muestra de 0.5413-g utilizando 10.00 mL de HCl 1.396 M. Después de calentar para expulsar CO 2, el exceso de HCl se tituló al punto final de fenolftaleína, requiriendo 39.96 mL de NaOH 0.1004 M. Reporte la pureza de la muestra como %w/w CaCo 3.
- Responder
-
El total de moles de HCl utilizados en este análisis es
\[(1.396 \ \mathrm{M})(0.01000 \ \mathrm{L})=1.396 \times 10^{-2} \ \mathrm{mol} \ \mathrm{HCl} \nonumber\]
Del total de moles de HCl
\[(0.1004 \ \mathrm{M} \ \mathrm{NaOH})(0.03996 \ \mathrm{L}) \times \frac{1 \ \mathrm{mol} \ \mathrm{HCl}}{\mathrm{mol} \ \mathrm{NaOH}} =4.012 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} \nonumber\]
se consumen en la valoración posterior con NaOH, lo que significa que
\[ 1.396 \times 10^{-2} \ \mathrm{mol} \ \mathrm{HCl}-4.012 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} \\ =9.95 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} \nonumber\]
reaccionar con el CaCo 3. Debido a que\(\text{CO}_3^{2-}\) es dibásico, cada mol de CaCo 3 consume dos moles de HCl; así
\[9.95 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HCl} \times \frac{1 \ \mathrm{mol} \ \mathrm{CaCO}_{3}}{2 \ \mathrm{mol} \ \mathrm{HCl}} \times \\ \frac{100.09 \ \mathrm{g} \ \mathrm{CaCO}_{3}}{\mathrm{mol} \ \mathrm{CaCO}_{3}}=0.498 \ \mathrm{g} \ \mathrm{CaCO}_{3} \nonumber\]
\[\frac{0.498 \ \mathrm{g} \ \mathrm{CaCO}_{3}}{0.5143 \ \mathrm{g} \text { sample }} \times 100=96.8 \ \% \mathrm{w} / \mathrm{w} \ \mathrm{CaCO}_{3} \nonumber\]
Anteriormente notamos que podemos usar una titulación ácido-base para analizar una mezcla de ácidos o bases titulando a más de un punto de equivalencia. La concentración de cada analito se determina contabilizando su contribución a cada punto de equivalencia.
La alcalinidad de las aguas naturales suele ser controlada por OH —\(\text{HCO}_3^-\), y\(\text{CO}_3^{2-}\), presente singularmente o en combinación. Titular una muestra de 100.0 mL a un pH de 8.3 requiere 18.67 mL de HCl 0.02812 M. Una segunda alícuota de 100.0-mL requiere 48.12 mL del mismo valorante para alcanzar un pH de 4.5. Identificar las fuentes de alcalinidad y sus concentraciones en miligramos por litro.
Solución
Debido a que el volumen de titulante para alcanzar un pH de 4.5 es más del doble del necesario para alcanzar un pH de 8.3, sabemos por la Tabla 9.2.5 , que la alcalinidad de la muestra está controlada por\(\text{CO}_3^{2-}\) y\(\text{HCO}_3^-\). Titulación a un pH de 8.3 neutraliza\(\text{CO}_3^{2-}\) a\(\text{HCO}_3^-\)
\[\mathrm{CO}_{3}^{2-}(a q)+\mathrm{HCl}(a q) \rightarrow \mathrm{HCO}_{3}^{-}(a q)+\mathrm{Cl}^{-}(a q) \nonumber\]
pero no hay reacción entre el valorante y\(\text{HCO}_3^-\) (ver Figura 9.2.14 ). La concentración de\(\text{CO}_3^{2-}\) en la muestra, por lo tanto, es
\[{(0.02812 \ \mathrm{M \ HCl})(0.01867 \ \mathrm{L \ HCl}) \times} {\frac{1 \ \mathrm{mol} \ \mathrm{CO}_3^{2-}}{\mathrm{mol} \ \mathrm{HCl}}=5.250 \times 10^{-4} \ \mathrm{mol} \ \mathrm{CO}_{3}^{2-}} \nonumber\]
\[\frac{5.250 \times 10^{-4} \ \mathrm{mol} \ \mathrm{CO}_{3}^{2-}}{0.1000 \ \mathrm{L}} \times \frac{60.01 \ \mathrm{g} \ \mathrm{CO}_{3}^{2-}}{\mathrm{mol} \ \mathrm{CO}_{3}^{2-}} \times \frac{1000 \ \mathrm{mg}}{\mathrm{g}}=315.1 \ \mathrm{mg} / \mathrm{L} \nonumber\]
Titulación a un pH de 4.5 neutraliza\(\text{CO}_3^{2-}\) a H 2 CO 3 y neutraliza\(\text{HCO}_3^-\) a H 2 CO 3 (ver Figura 9.2.14 ).
\[\begin{array}{l}{\mathrm{CO}_{3}^{2-}(a q)+2 \mathrm{HCl}(a q) \rightarrow \mathrm{H}_{2} \mathrm{CO}_{3}(a q)+2 \mathrm{Cl}^{-}(a q)} \\ {\mathrm{HCO}_{3}^{-}(a q)+\mathrm{HCl}(a q) \rightarrow \mathrm{H}_{2} \mathrm{CO}_{3}(a q)+\mathrm{Cl}^{-}(a q)}\end{array} \nonumber\]
Debido a que sabemos cuántos moles\(\text{CO}_3^{2-}\) hay en la muestra, podemos calcular el volumen de HCl que consume.
\[{5.250 \times 10^{-4} \ \mathrm{mol} \ \mathrm{CO}_{3}^{2-} \times \frac{2 \ \mathrm{mol} \ \mathrm{HCl}}{\mathrm{mol} \ \mathrm{CO}_{3}^{2-}} \times} {\frac{1 \ \mathrm{L} \ \mathrm{HCl}}{0.02812 \ \mathrm{mol} \ \mathrm{HCl}} \times \frac{1000 \ \mathrm{mL}}{\mathrm{L}}=37.34 \ \mathrm{mL} \ \mathrm{HCl}} \nonumber\]
Esto deja 48.12 ml—37.34 mL, o 10.78 mL de HCl para reaccionar\(\text{HCO}_3^-\). La cantidad de\(\text{HCO}_3^-\) en la muestra es
\[{(0.02812 \ \mathrm{M \ HCl})(0.01078 \ \mathrm{L} \ \mathrm{HCl}) \times} {\frac{1 \ \mathrm{mol} \ \mathrm{H} \mathrm{CO}_{3}^{-}}{\mathrm{mol} \ \mathrm{HCl}}=3.031 \times 10^{-4} \ \mathrm{mol} \ \mathrm{HCO}_{3}^{-}} \nonumber\]
La muestra contiene 315.1\(\text{CO}_3^{2-}\) mg/L y 185.0\(\text{HCO}_3^-\) mg/L
Las muestras que contienen una mezcla de los ácidos débiles monopróticos 2—cloruro de metilanilinio (C 7 H 10 NCl, p K a = 4.447) y 3—nitrofenol (C 6 H 5 NO 3, p K a = 8.39) pueden analizarse mediante titulación con NaOH. Una muestra de 2.006-g requiere 19.65 mL de NaOH 0.200 M para alcanzar el punto final de bromocresol púrpura y 48.41 mL de NaOH 0.200 M para alcanzar el punto final de fenolftaleína. Reporte el% w/w de cada compuesto en la muestra.
- Responder
-
De los dos analitos, el 2-metilanilinio es el ácido más fuerte y es el primero en reaccionar con el valorante. La valoración al punto final de bromocresol púrpura, por lo tanto, proporciona información sobre la cantidad de 2-metilanilinio en la muestra.
\[(0.200\ \mathrm{M} \ \mathrm{NaOH} )(0.01965 \ \mathrm{L}) \times \frac{1 \ \mathrm{mol} \ \mathrm{C}_{7} \mathrm{H}_{10} \mathrm{NCl}}{\mathrm{mol} \ \mathrm{NaOH}} \times \frac{143.61 \ \mathrm{g} \ \mathrm{C}_{7} \mathrm{H}_{10} \mathrm{NCl}}{\mathrm{mol} \ \mathrm{C}_{7} \mathrm{H}_{10} \mathrm{NCl}}=0.564 \ \mathrm{g} \ \mathrm{C}_{7} \mathrm{H}_{10} \mathrm{NCl} \nonumber\]
\[\frac{0.564 \ \mathrm{g} \ \mathrm{C}_{7} \mathrm{H}_{10} \mathrm{NCl}}{2.006 \ \mathrm{g} \text { sample }} \times 100=28.1 \ \% \mathrm{w} / \mathrm{w} \ \mathrm{C}_{7} \mathrm{H}_{10} \mathrm{NCl} \nonumber\]
Titulación desde el punto final de bromocresol púrpura hasta el punto final de fenolftaleína, un total de 48.41 mL — 19.65 mL = 28.76 mL, da la cantidad de NaOH que reacciona con 3-nitrofenol. La cantidad de 3-nitrofenol en la muestra, por lo tanto, es
\[(0.200 \ \mathrm{M} \ \mathrm{NaOH}) (0.02876 \ \mathrm{L}) \times \frac{1 \ \mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NO}_{3}}{\mathrm{mol} \ \mathrm{NaOH}} \times \frac{139.11 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NO}_{3}}{\mathrm{mol} \ \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NO}_{3}}=0.800 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NO}_{3} \nonumber\]
\[\frac{0.800 \ \mathrm{g} \ \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NO}_{3}}{2.006 \ \mathrm{g} \text { sample }} \times 100=39.8 \ \% \mathrm{w} / \mathrm{w} \ \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NO}_{3} \nonumber\]
Aplicaciones Cualitativas
El Ejemplo 9.5 muestra cómo podemos usar una titulación ácido-base para determinar las formas de alcalinidad en las aguas y sus concentraciones. Podemos extender este enfoque a otros sistemas. Por ejemplo, si valoramos una muestra al punto final de naranja de metilo y al punto final de fenolftaleína usando un ácido fuerte o una base fuerte, podemos determinar cuáles de las siguientes especies están presentes y sus concentraciones: H 3 PO 4,\(\text{H}_2\text{PO}_4^-\),\(\text{HPO}_4^{2-}\),\(\text{PO}_4^{3-}\), HCl, y NaOH. Como se indica en la Tabla 9.2.8 , cada especie o mezcla de especies tiene una relación única entre los volúmenes de titulante necesarios para alcanzar estos dos puntos finales. Nótese que las mezclas que contengan tres o más de estas especies no son posibles.
Usa un diagrama de escalera para convencerte de que las mezclas que contienen tres o más de estas especies son inestables.
Aplicaciones de Caracterización
Además de un análisis cuantitativo y un análisis cualitativo, también podemos utilizar una titulación ácido-base para caracterizar las propiedades químicas y físicas de la materia. Dos aplicaciones de caracterización útiles son la determinación del peso equivalente de un compuesto y la determinación de su constante de disociación ácida o su constante de disociación de bases.
Pesos Equivalentes
Supongamos que valoramos una muestra de un ácido débil impuro a un punto final bien definido usando una base fuerte monoprótica como valorante. Si asumimos que la titulación implica la transferencia de n protones, entonces los moles de titulante necesarios para alcanzar el punto final son
\[\text { moles titrant }=\frac{n \text { moles titrant }}{\text { moles analyte }} \times \text { moles analyte } \nonumber\]
Si conocemos la identidad del analito, podemos usar esta ecuación para determinar la cantidad de analito en la muestra
\[\text { grams analyte }=\text { moles titrant } \times \frac{1 \text { mole analyte }}{n \text { moles analyte }} \times F W \text { analyte } \nonumber\]
donde FW es el peso de la fórmula del analito.
Pero, ¿y si no conocemos la identificación del analito? Si valoramos una muestra pura del analito, podemos obtener alguna información útil que puede ayudarnos a establecer su identidad. Debido a que no conocemos el número de protones que se titulan, dejamos n = 1 y reemplazamos el peso de la fórmula del analito por su peso equivalente (EW)
\[\text { grams analyte }=\text { moles titrant } \times \frac{1 \text { equivalent analyte }}{1 \text { mole analyte }}=E W \text { analyte } \nonumber\]
donde
\[F W=n \times E W \nonumber\]
Una muestra de 0.2521-g de un ácido débil desconocido se titula con NaOH 0.1005 M, requiriendo 42.68 mL para alcanzar el punto final de fenolftaleína. Determinar el peso equivalente del compuesto. ¿Cuál de los siguientes compuestos es más probable que sea el ácido débil desconocido?
| ácido | fórmula | peso de la fórmula (g/mol) | tipo |
|---|---|---|---|
| ácido ascórbico | C 8 H 8 O 6 | 176.1 | monoprótico |
| ácido malónico | C 3 H 4 O 4 | 104.1 | diprótico |
| ácido succínico | C 4 H 6 O4 | 118.1 | diprótico |
| ácido cítrico | C 6 H 8 O 7 | 192.1 | triprótico |
Solución
Los moles de NaOH necesarios para alcanzar el punto final son
\[(0.1005 \ \mathrm{M} \ \mathrm{NaOH})(0.04268 \ \mathrm{L} \ \mathrm{NaOH})=4.289 \times 10^{-3} \ \mathrm{mol} \ \mathrm{NaOH} \nonumber\]
Los equivalentes de ácido débil son los mismos que los moles de NaOH utilizados en la titulación; así, el peso equivalente del analito es
\[E W=\frac{0.2521 \ \mathrm{g}}{4.289 \times 10^{-3} \text { equivalents }}=58.78 \ \mathrm{g} / \mathrm{equivalent} \nonumber\]
Los pesos de fórmula posibles para el ácido débil son 58.78 g/mol (n = 1), 117.6 g/mol (n = 2) y 176.3 g/mol (n = 3). Si el analito es un ácido débil monoprótico, entonces su peso de fórmula es de 58.78 g/mol, eliminando como posibilidad el ácido ascórbico. Si se trata de un ácido diprótico débil, entonces el peso de la fórmula del analito es 58.78 g/mol o 117.6 g/mol, dependiendo de si el ácido débil se tituló a su primer o segundo punto de equivalencia. El ácido succínico, con un peso de fórmula de 118.1 g/mol es una posibilidad, pero el ácido malónico no lo es. Si el analito es un ácido triprótico débil, entonces su peso de fórmula es 58.78 g/mol, 117.6 g/mol, o 176.3 g/mol. Ninguno de estos valores está cerca del peso de fórmula para el ácido cítrico, eliminándolo como posibilidad. Solo el ácido succínico proporciona una posible coincidencia.
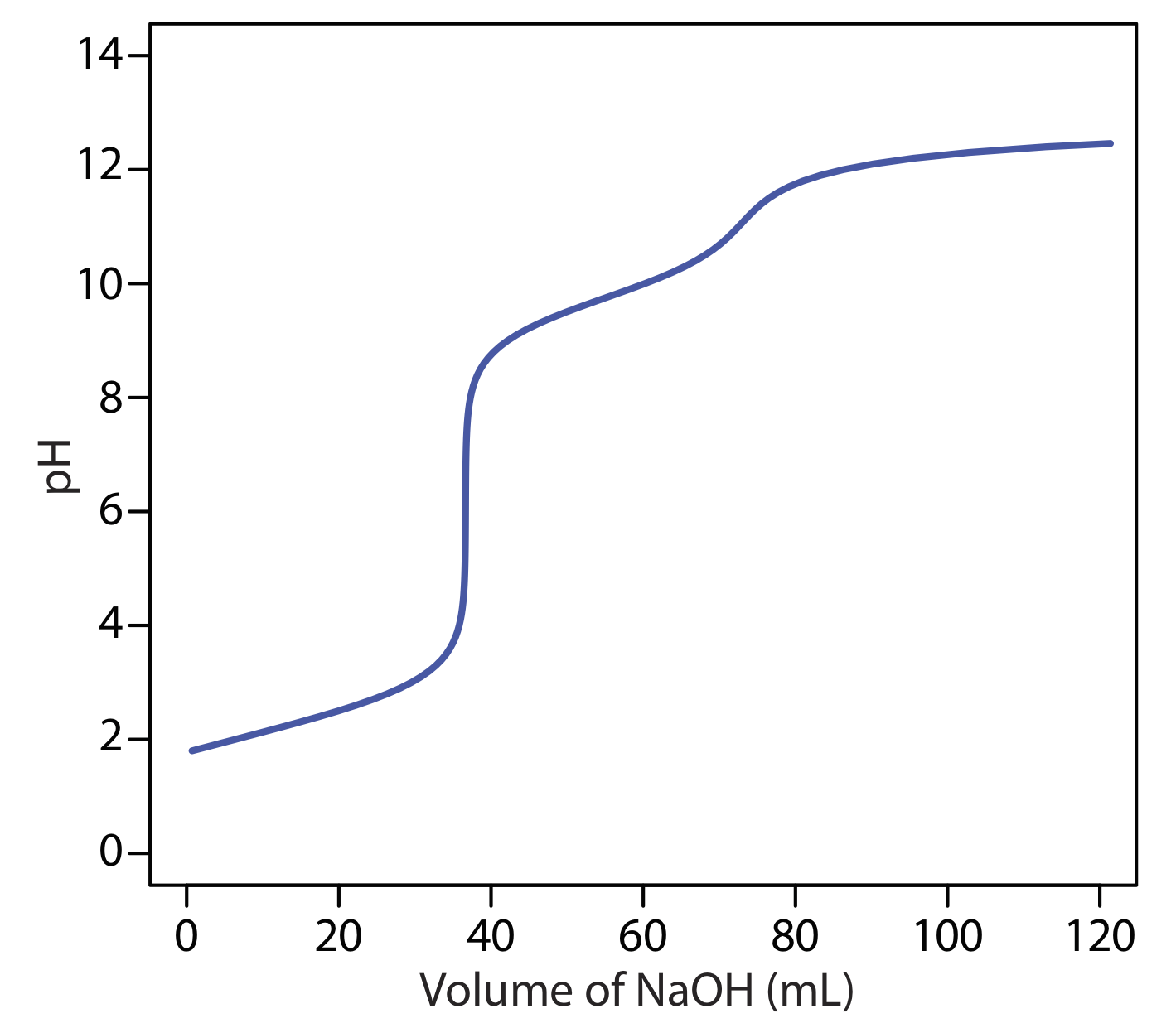
La Figura 9.2.16 muestra la curva de valoración potenciométrica para la valoración de una muestra de 0.500-g de un ácido débil desconocido. El valorante es NaOH 0.1032 M. ¿Cuál es el peso equivalente del ácido débil?
- Responder
-
El primero de los dos puntos finales visibles es aproximadamente 37 mL de NaOH. El peso equivalente del analito, por lo tanto, es
\[(0.1032 \ \mathrm{M} \ \mathrm{NaOH})(0.037 \ \mathrm{L}) \times \frac{1 \text { equivalent }}{\mathrm{mol} \ \mathrm{NaOH}}=3.8 \times 10^{-3} \text { equivalents } \nonumber\]
\[E W=\frac{0.5000 \ \mathrm{g}}{3.8 \times 10^{-3} \text { equivalents }}=1.3 \times 10^{2} \ \mathrm{g} / \mathrm{equivalent} \nonumber\]
Constantes de equilibrio
Otra aplicación de la titrimetría ácido-base es la determinación de una constante de disociación de un ácido débil o de una base débil. Consideremos, por ejemplo, una solución de ácido acético, CH 3 COOH, para la cual la constante de disociación es
\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \nonumber\]
Cuando las concentraciones de CH 3 COOH y CH 3 COO — son iguales, la expresión de K a se reduce a K a = [H 3 O +], o pH = p K a. Si valoramos una solución de ácido acético con NaOH, el pH es igual al p K a cuando el volumen de NaOH es aproximadamente 1⁄2 V eq. Como se muestra en la Figura 9.2.17 , una curva de titulación potenciométrica proporciona una estimación razonable de p K a de ácido acético.
Recordemos que pH = p K a es un escalón en un diagrama de escalera, que divide el eje del pH en dos regiones, una donde el ácido débil es la especie predominante, y otra donde su base débil conjugada es la especie predominante.
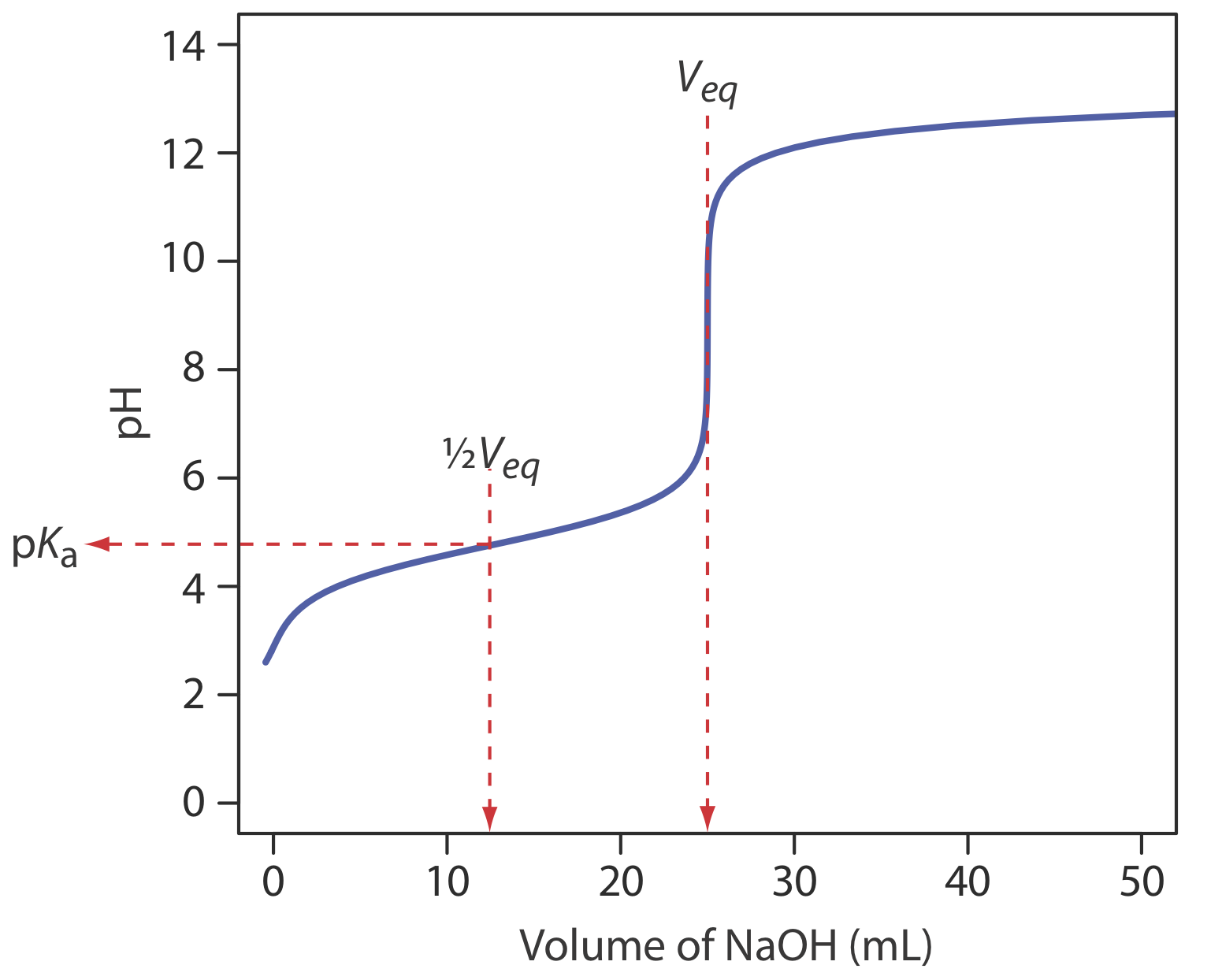
Este método proporciona una estimación razonable para la p K a de un ácido débil si el ácido no es ni demasiado fuerte ni demasiado débil. Estas limitaciones son fáciles de apreciar si consideramos dos casos limitantes. Para el primer caso limitante, supongamos que el ácido débil, HA, está más del 50% disociado antes de que comience la titulación (un valor K a relativamente grande); en este caso la concentración de HA antes del punto de equivalencia siempre es menor que la concentración de A — y hay ningún punto en la curva de titulación donde [HA] = [A —]. En el otro extremo, si el ácido es demasiado débil, entonces menos del 50% del ácido débil reacciona con el valorante en el punto de equivalencia. En este caso la concentración de HA antes del punto de equivalencia siempre es mayor que la de A —. Determinar la p K a por el método del punto de media equivalencia sobreestima su valor si el ácido es demasiado fuerte y subestima su valor si el ácido es demasiado débil.
Utilice la curva de valoración potenciométrica de la Figura 9.2.16 para estimar los valores de p K a para el ácido débil en el Ejercicio 9.2.10 .
- Responder
-
A 1⁄2 V eq, o aproximadamente 18.5 mL, el pH es aproximadamente 2.2; así, estimamos que la p K a del analito es 2.2.
Un segundo enfoque para determinar la p K a de un ácido débil es usar una parcela Gran. Por ejemplo, anteriormente en este capítulo derivamos la siguiente ecuación para la titulación de un ácido débil con una base fuerte.
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \times V_{b}=K_{a} V_{e q}-K_{a} V_{b} \nonumber\]
Una gráfica de [H 3 O +]\(\times\) V b versus V b para volúmenes menores que el punto de equivalencia produce una línea recta con una pendiente de — K a. Se han desarrollado otras linealizaciones que utilizan toda la curva de titulación o que no requieren suposiciones [(a) González, A. G.; Asuero, A. G. Anal. Chim. Acta 1992, 256, 29—33; b) Papanastasiou, G.; Ziogas, I.; Kokkindis, G. Anal. Chim. Acta 1993, 277, 119—135]. Este enfoque para determinar una constante de acidez se ha utilizado para estudiar las propiedades ácido-base de los ácidos húmicos, que son ácidos orgánicos de gran peso molecular de origen natural con múltiples sitios ácidos. En un estudio se encontró que un ácido húmico tenía seis sitios titulables, tres los cuales se identificaron como ácidos carboxílicos, dos los cuales se creían eran aminas secundarias o terciarias, y uno el cual se identificó como un grupo fenólico [Alexio, L. M.; Godinho, O. E. S.; da Costa, W. F. Anal. Chim. Acta 1992, 257, 35—39].
Los valores de K a determinados por este método pueden tener un error sustancial si se ignora el efecto de la actividad. Véase el Capítulo 6.9 para una discusión de actividad.
Evaluación de la Titrimetría Ácido-Base
Escala de Operación
En una valoración ácido-base, el volumen de valorante necesario para alcanzar el punto de equivalencia es proporcional a los moles de titulación. Debido a que el pH del valorador o del valorante es una función de su concentración, el cambio en el pH en el punto de equivalencia y, por lo tanto, la viabilidad de una titulación ácido-base, depende de sus respectivas concentraciones. La Figura 9.2.18 , por ejemplo, muestra una serie de curvas de titulación para la titulación de varias concentraciones de HCl con soluciones equimolares NaOH. Para concentraciones de titrand y valorante menores de 10 —3 M, el cambio en el pH en el punto final es demasiado pequeño para proporcionar un resultado preciso y preciso.
La titrimetría ácido-base es un ejemplo de una técnica de análisis total en la que la señal es proporcional a la cantidad absoluta de analito. Consulte el Capítulo 3 para una discusión de la diferencia entre las técnicas de análisis total y las técnicas de concentración.
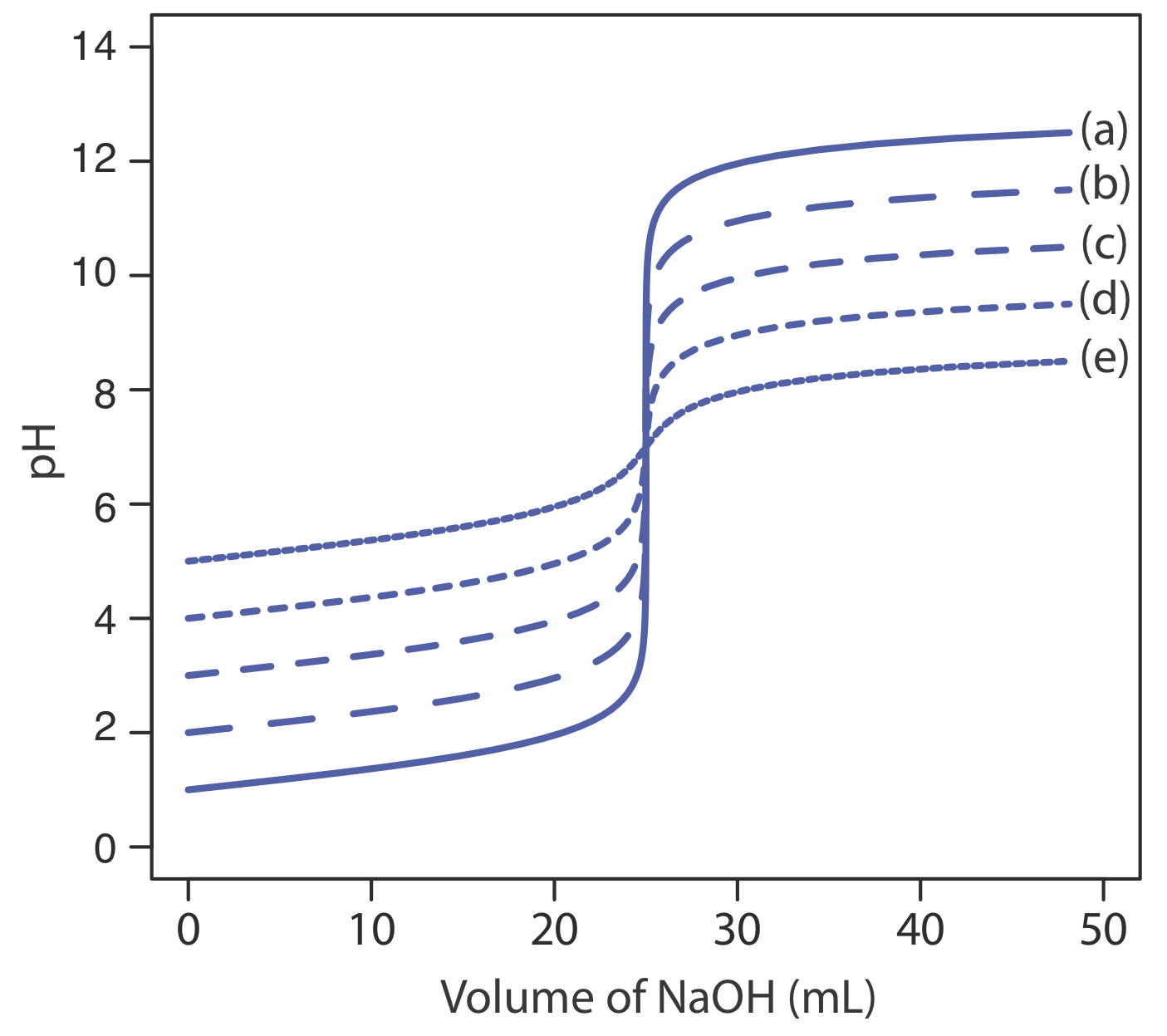
Una concentración mínima de 10 —3 M pone límites a la menor cantidad de analito que podemos analizar con éxito. Por ejemplo, supongamos que nuestro analito tiene un peso de fórmula de 120 g/mol. Para monitorear con éxito el punto final de la titulación usando un indicador o una sonda de pH, el campo de valoración necesita un volumen inicial de aproximadamente 25 mL. Si asumimos que el peso de la fórmula del analito es de 120 g/mol, entonces cada muestra debe contener al menos 3 mg de analito. Por esta razón, las titulaciones ácido-base generalmente se limitan a analitos mayores y menores. Podemos extender el análisis de gases para rastrear analitos al extraer un gran volumen del gas a través de una solución de recolección adecuada.
Necesitamos un volumen de titrand suficiente para cubrir la punta de la sonda de pH o para permitir una fácil observación del color del indicador. Un volumen de 25 mL no es una estimación irrazonable del volumen mínimo.
Un objetivo de la química analítica es extender los análisis a muestras más pequeñas. Aquí se describen dos enfoques interesantes para la titulación de muestras μL y pL. En un diseño experimental (Figura 9.2.19 ), se mantienen muestras de 20—100 μL por acción capilar entre un electrodo de pH de superficie plana y una etapa de muestra de acero inoxidable [Steele, A.; Hieftje, G. M. Anal. Chem. 1984, 56, 2884—2888]. El valorante se agrega usando las oscilaciones de un dispositivo cerámico piezoeléctrico para mover una varilla de vidrio en ángulo dentro y fuera de un tubo conectado a un depósito que contiene el valorante. Cada vez que se retira el tubo de vidrio se libera una microgotita de aproximadamente 2 nL de valorante. Las microgotas se dejan caer sobre la muestra, con la mezcla realizada girando la etapa de muestra a 120 rpm. Se dispensa un total de 450 microgotas, con un volumen combinado de 0.81—0.84 μL entre cada medición de pH. De esta manera se construye una curva de titulación. Este método se ha utilizado para valorar soluciones de HCl 0.1 M y CH 3 COOH 0.1 M con NaOH 0.1 M. Los errores absolutos variaron de un mínimo de +0.1% a un máximo de — 4.1%, con desviaciones estándar relativas de 0.15% a 4.7%. Muestras tan pequeñas como 20 μL fueron tituladas exitosamente.
Otro enfoque realiza la titulación ácido-base en una sola gota de solución [(a) Gratzl, M.; Yi, C. Anal. Chem. 1993, 65, 2085—2088; b) Yi, C.; Gratzl, M. Anal. Chem. 1994, 66, 1976—1982; c) Hui, K. Y.; Gratzl, M. Anal. Chem. 1997, 69, 695—698; d) Yi, C.; Huang, D.; Gratzl, M. Anal. Chem. 1996, 68, 1580—1584; e) Xie, H.; Gratzl, M. Anal. Chem. 1996, 68, 3665—3669]. El valorante se administra usando una microbureta fabricada a partir de una micropipeta capilar de vidrio (Figura 9.2.20 ). La microbureta tiene una punta de 1-2 μm llena con una membrana de gel de agar. La punta de la microbureta se coloca dentro de una gota de la solución de muestra, la cual se suspende en heptano, y se deja que el titulante se difunda en la muestra. El progreso de la titulación se monitorea mediante un indicador ácido-base y se mide el tiempo necesario para llegar al punto final. La velocidad de difusión del valorante desde la microbureta se determina mediante una calibración previa. Una vez calibrado el tiempo de punto final se convierte en un volumen de punto final. Las muestras generalmente consisten en volúmenes de picolitros (10 —12 litros), siendo la muestra más pequeña 0.7 pL. La precisión de las titulaciones es de aproximadamente 2%.
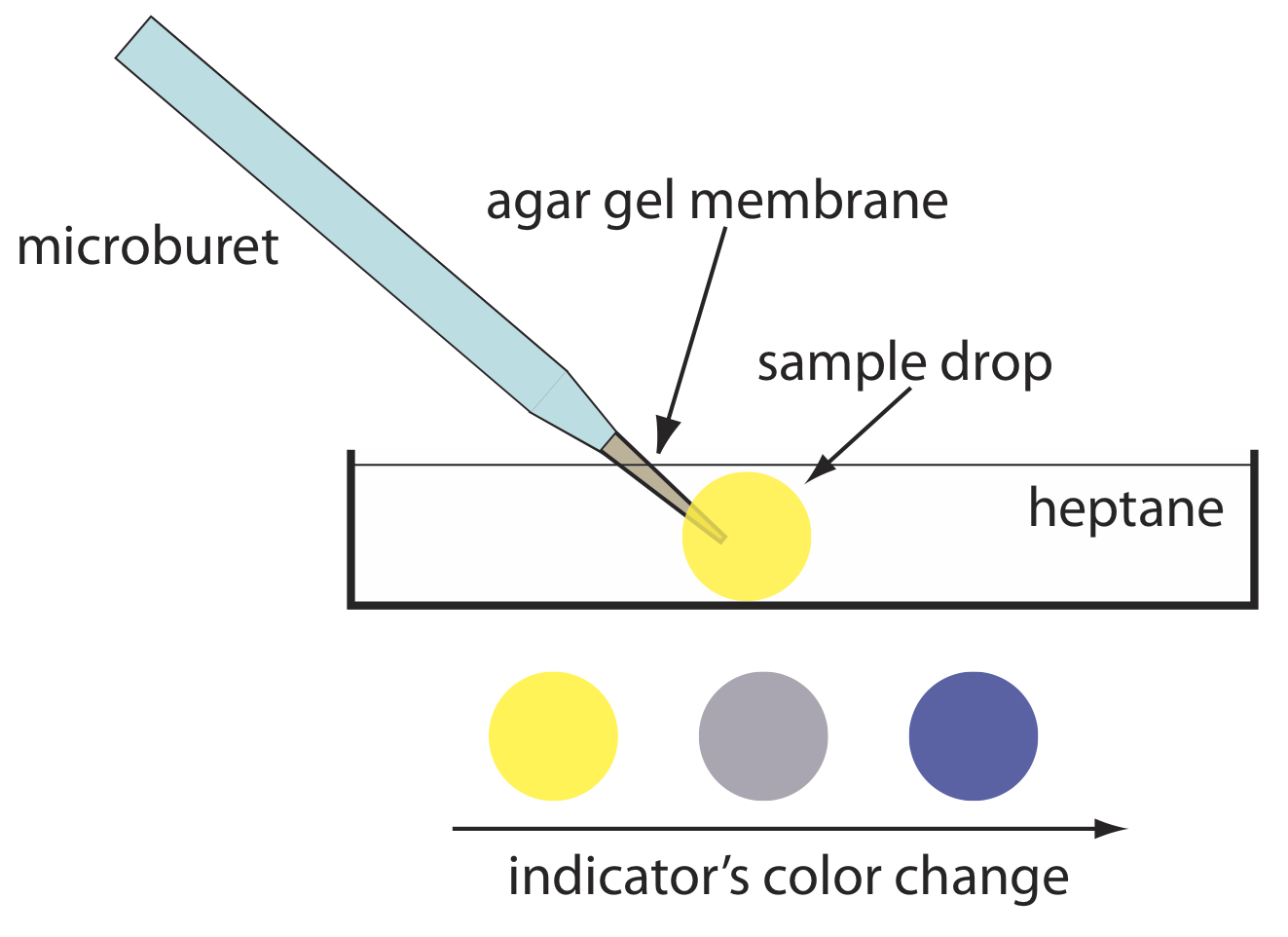
Las titulaciones realizadas con volúmenes de muestra de microlitros o picolitros requieren una menor cantidad absoluta de analito. Por ejemplo, se han realizado valoraciones difusionales en tan solo 29 femtomoles (10 —15 moles) de ácido nítrico. Sin embargo, el analito debe estar presente en la muestra a un nivel mayor o menor para que la titulación dé resultados precisos y precisos.
Precisión
Cuando se trabaja con una macro-mayor o una macro-menor, una titulación ácido-base puede lograr un error relativo de 0.1— 0.2%. La principal limitación a la precisión es la diferencia entre el punto final y el punto de equivalencia.
Precisión
La precisión relativa de una titulación ácido-base depende principalmente de la precisión con la que podemos medir el volumen del punto final y la precisión en la detección del punto final. En condiciones óptimas, una valoración ácido-base tiene una precisión relativa de 0.1— 0.2%. Podemos mejorar la precisión relativa utilizando la mayor bureta posible y asegurando que usamos la mayor parte de su capacidad para llegar al punto final. Una bureta de menor volumen es una mejor opción cuando se usan reactivos costosos, cuando la eliminación de desechos es una preocupación o cuando debemos completar la titulación rápidamente para evitar reacciones químicas competitivas. Un valorador automático es particularmente útil para valoraciones que requieren pequeños volúmenes de valorante porque proporciona una precisión significativamente mejor (típicamente alrededor de ± 0.05% del volumen de la bureta).
La precisión de detección del punto final depende de cómo se mide y de la pendiente de la curva de titulación en el punto final. Con un indicador la precisión de la señal del punto final suele ser ±0.03—0.10 mL. Los puntos finales potenciométricos suelen ser más precisos.
Sensibilidad
Para una valoración ácido-base podemos escribir la siguiente ecuación analítica general para expresar el volumen del valorante en términos de la cantidad de titulacion
\[\text { volume of titrant }=k \times \text { moles of titrand } \nonumber\]
donde k, la sensibilidad, está determinada por la estequiometría entre el campo de valoración y el valorante. Consideremos, por ejemplo, la determinación de ácido sulfuroso, H 2 SO 3, valorando con NaOH al primer punto de equivalencia
\[\mathrm{H}_{2} \mathrm{SO}_{3}(a q)+\mathrm{OH}^{-}(a q) \rightarrow \mathrm{H}_{2} \mathrm{O}(l )+\mathrm{HSO}_{3}^{-}(a q) \nonumber\]
En el punto de equivalencia la relación entre los moles de NaOH y los moles de H 2 SO 3 es
\[\mathrm{mol} \ \mathrm{NaOH}=\mathrm{mol} \ \mathrm{H}_{2} \mathrm{SO}_{3} \nonumber\]
Sustituyendo la molaridad y el volumen del valorante por los moles de NaOH y reordenando
\[M_{\mathrm{NaOH}} \times V_{\mathrm{NNOH}}=\mathrm{mol} \ \mathrm{H}_{2} \mathrm{SO}_{3} \nonumber\]
\[V_{\mathrm{NaOH}}=\frac{1}{M_{\mathrm{NaOH}}} \times \mathrm{mol} \ \mathrm{H}_{2} \mathrm{SO}_{3} \nonumber\]
encontramos que k es
\[k=\frac{1}{M_{\mathrm{NaOH}}} \nonumber\]
Hay dos formas en las que podemos mejorar la sensibilidad de una titulación. El primero, y más obvio, es disminuir la concentración del titulante porque es inversamente proporcional a la sensibilidad, k. El segundo enfoque, que sólo se aplica si la titrand es multiprótica, consiste en valorar a un punto de equivalencia posterior. Si valoramos H 2 SO 3 a su segundo punto de equivalencia
\[ \mathrm{H}_{2} \mathrm{SO}_{3}(a q)+2 \mathrm{OH}^{-}(a q) \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{SO}_{3}^{2-}(a q)\nonumber\]
entonces cada mol de H 2 SO 3 consume dos moles de NaOH
\[\mathrm{mol} \ \mathrm{NaOH}=2 \times \mathrm{mol} \ \mathrm{H}_{2} \mathrm{SO}_{3} \nonumber\]
y la sensibilidad se vuelve
\[k=\frac{2}{M_{\mathrm{NaOH}}} \nonumber\]
En la práctica, sin embargo, cualquier mejora en la sensibilidad se compensa con una disminución en la precisión del punto final si un mayor volumen de valorador requiere que rellenemos la bureta. Por esta razón, los procedimientos estándar de titulación ácido-base se escriben para asegurar que una titulación utilice 60— 100% del volumen de la bureta.
Selectividad
Los titulantes ácido-base no son selectivos. Un valorante de base fuerte, por ejemplo, reacciona con todos los ácidos de una muestra, independientemente de sus fortalezas individuales. Si la titrand contiene un analito y un interferente, entonces la selectividad depende de sus fuerzas ácidas relativas. Consideremos dos situaciones limitantes.
Si el analito es un ácido más fuerte que el interferente, entonces el valorante reaccionará con el analito antes de que comience a reaccionar con el interferente. La viabilidad del análisis depende de si la reacción del valorante con el interferente afecta la ubicación exacta del punto de equivalencia del analito. Si las constantes de disociación ácida son sustancialmente diferentes, el punto final para el analito se puede determinar con precisión. Por el contrario, si las constantes de disociación ácida para el analito y el interferente son similares, entonces puede que no haya un punto final preciso para el analito. En este último caso no es posible realizar un análisis cuantitativo para el analito.
En la segunda situación limitante el analito es un ácido más débil que el interferente. En este caso, el volumen de valorante necesario para alcanzar el punto de equivalencia del analito está determinado por la concentración tanto del analito como del interferente. Para dar cuenta de la contribución del interferente al punto final, debe estar disponible un punto final para el interferente. Nuevamente, si las constantes de disociación ácida para el analito y el interferente son significativamente diferentes, entonces la determinación del analito es posible. Sin embargo, si las constantes de disociación ácida son similares, solo hay un único punto de equivalencia y no podemos separar las contribuciones del analito y del interferente al volumen del punto de equivalencia.
Tiempo, Costo y Equipo
Las titulaciones ácido-base requieren menos tiempo que la mayoría de los procedimientos gravimétricos, pero más tiempo que muchos métodos instrumentales de análisis, particularmente cuando se analizan muchas muestras. Con un valorador automático, sin embargo, las preocupaciones sobre el tiempo de análisis son menos significativas. Al realizar una valoración manualmente, nuestro equipo necesita, una bureta y, tal vez, un medidor de pH, son pocos en número, son económicos, están disponibles de forma rutinaria y son fáciles de mantener. Los valoradores automáticos están disponibles por entre $3000 y $10 000.