9.3: Titulación de complejación
- Page ID
- 75401
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los primeros ejemplos de titulaciones de complejación metal-ligando son las determinaciones de Liebig, en la década de 1850, de cianuro y cloruro utilizando, respectivamente, Ag + y Hg 2 + como valorante. Las aplicaciones analíticas prácticas de la titrimetría de complejación fueron lentas de desarrollarse debido a que muchos metales y ligandos forman una serie de complejos metal-ligando. La valoración de CN de Liebig con Ag + fue exitosa porque forman un complejo único y estable de\(\text{Ag(CN)}_2^-\), lo que resulta en un único punto final de fácil identificación. Otros complejos metal-ligando, tales como\(\text{CdI}_4^{2-}\), no son analíticamente útiles porque forman una serie de complejos metal-ligando (CdI +, CdI 2 (aq)\(\text{CdI}_3^-\) y\(\text{CdI}_4^{2-}\)) que producen una secuencia de puntos finales poco definidos.
Recordemos que una curva de valoración ácido-base para un ácido débil diprótico tiene un único punto final si sus dos valores K a no son suficientemente diferentes. Véase la Figura 9.2.6 para un ejemplo.
En 1945, Schwarzenbach introdujo los ácidos aminocarboxílicos como ligandos multidentados. El más utilizado de estos nuevos ligandos, el ácido etilendiaminotetraacético o EDTA, forma un fuerte complejo 1:1 con muchos iones metálicos. La disponibilidad de un ligando que da un único punto final fácilmente identificado hizo de la titrimetría de complejación un método analítico práctico.
Química y Propiedades del EDTA
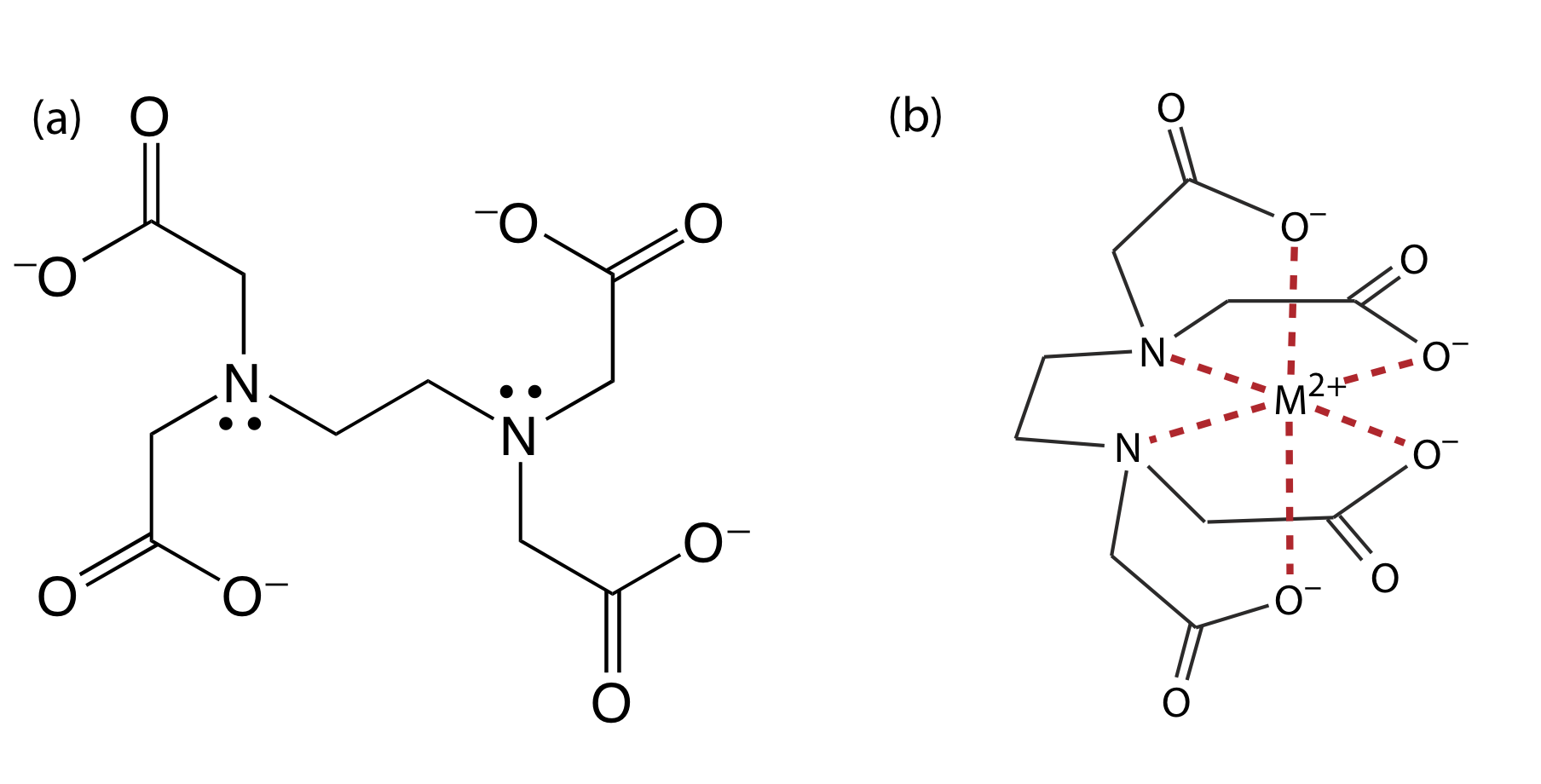
El ácido etilendiaminotetraacético, o EDTA, es un ácido aminocarboxílico. El EDTA, cuya estructura se muestra en la Figura 9.3.1 a en su forma completamente desprotonada, es un ácido de Lewis con seis sitios de unión, los cuatro grupos carboxilato cargados negativamente y los dos grupos amino terciarios, que pueden donar hasta seis pares de electrones a un ion metálico. El complejo metal-ligando resultante, en el que EDTA forma una estructura tipo jaula alrededor del ion metálico (Figura 9.3.1 b), es muy estable. El número real de sitios de coordinación depende del tamaño del ion metálico, sin embargo, todos los complejos metal-EDTA tienen una estequiometría 1:1.
Constantes de Formación Metal—EDTA
Para ilustrar la formación de un complejo metal-EDTA, consideremos la reacción entre Cd 2 + y EDTA
donde Y 4— es una notación taquigráfica para la forma completamente desprotonada de EDTA que se muestra en la Figura {{template.Index (ID:1)} a. Debido a que la constante de formación de la reacción
es grande, su posición de equilibrio se encuentra muy a la derecha. Las constantes de formación para otros complejos metal-EDTA se encuentran en el Apéndice 12.
El EDTA es un ácido débil
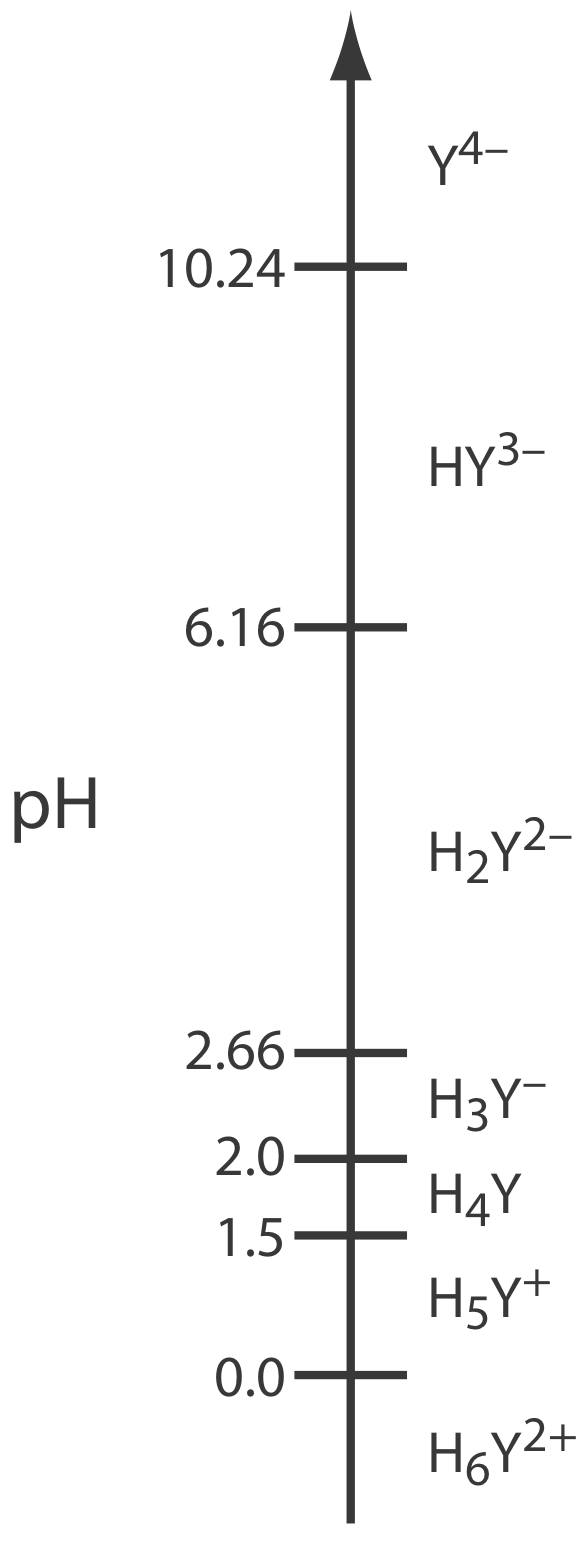
Además de sus propiedades como ligando, el EDTA también es un ácido débil. La forma completamente protonada de EDTA, H 6 Y 2+, es un ácido débil hexaprótico con sucesivos valores p K a de
\[\mathrm{p} K_\text{a1}=0.0 \quad \mathrm{p} K_\text{a2}=1.5 \quad \mathrm{p} K_\text{a3}=2.0 \nonumber\]
\[\mathrm{p} K_\text{a4}=2.66 \quad \mathrm{p} K_\text{a5}=6.16 \quad \mathrm{p} K_\text{a6}=10.24 \nonumber\]
Los primeros cuatro valores son para los protones de ácido carboxílico y los dos últimos valores son para los protones de amonio. La Figura 9.3.2 muestra un diagrama de escalera para EDTA. La forma específica de EDTA en reacción\ ref {9.1} es la especie predominante solo cuando el pH es más básico que 10.24.
Constantes condicionales de formación de metal-ligando
La constante de formación para CdY 2— en la Ecuación\ ref {9.2} asume que EDTA está presente como Y 4—. Debido a que el EDTA tiene muchas formas, cuando preparamos una solución de EDTA la conocemos concentración total, C EDTA, no la concentración de una forma específica, como Y 4—. Para usar la Ecuación\ ref {9.2}, necesitamos reescribirla en términos de C EDTA.
A cualquier pH, un balance de masas sobre EDTA requiere que su concentración total sea igual a las concentraciones combinadas de cada una de sus formas.
\[C_{\mathrm{EDTA}}=\left[\mathrm{H}_{6} \mathrm{Y}^{2+}\right]+\left[\mathrm{H}_{5} \mathrm{Y}^{+}\right]+\left[\mathrm{H}_{4} \mathrm{Y}\right]+\left[\mathrm{H}_{3} \mathrm{Y}^-\right]+\left[\mathrm{H}_{2} \mathrm{Y}^{2-}\right]+\left[\mathrm{HY}^{3-}\right]+\left[\mathrm{Y}^{4-}\right] \nonumber\]
Para corregir la constante de formación de las propiedades ácido-base del EDTA necesitamos calcular la fracción,\(\alpha_{\text{Y}^{4-}}\), de EDTA que está presente como Y 4—.
\[\alpha_{\text{Y}^{4-}}=\frac{\left[\text{Y}^{4-}\right]}{C_\text{EDTA}} \label{9.3}\]
El cuadro 9.3.1 proporciona valores de\(\alpha_{\text{Y}^{4-}}\) para los niveles de pH seleccionados. Resolviendo la Ecuación\ ref {9.3} para [Y 4—] y sustituyendo en la Ecuación\ ref {9.2} para la constante de formación CdY 2—
\[K_{\mathrm{f}}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] (\alpha_{\mathrm{Y}^{4-}}) C_{\mathrm{EDTA}}} \nonumber\]
y reorganizar da
donde\(K_f^{\prime}\) es una constante de formación condicional dependiente del pH. Como se muestra en la Tabla 9.3.2 , la constante de formación condicional para CDy 2— se vuelve más pequeña y el complejo se vuelve menos estable a pH más ácidos.
EDTA compite con otros ligandos
Para mantener un pH constante durante una titulación de complejación, generalmente se agrega un agente tampón. Si uno de los componentes del tampón es un ligando que se une con Cd 2 +, entonces el EDTA debe competir con el ligando por Cd 2 +. Por ejemplo, un\(\text{NH}_4^+ / \text{NH}_3\) tampón incluye NH 3, que forma varios complejos estables de Cd 2 + -NH 3. Debido a que el EDTA forma un complejo más fuerte con Cd 2 + que el NH 3, desplaza al NH 3; sin embargo, la estabilidad del complejo Cd 2 + —EDTA disminuye.
Podemos dar cuenta del efecto de un agente complejante auxiliar, como NH 3, de la misma manera que se contabilizó el efecto del pH. Antes de agregar EDTA, el balance de masas en Cd 2 +, C Cd, es
\[C_{\mathrm{Cd}} = \left[\mathrm{Cd}^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{2}^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right] + \left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{4}^{2+}\right] \nonumber\]
y la fracción de Cd 2 + no complejado,\(\alpha_{Cd^{2+}}\), es
\[\alpha_{\mathrm{Cd}^{2+}}=\frac{\left[\mathrm{Cd}^{2+}\right]}{C_{\mathrm{Cd}}} \label{9.5}\]
El valor de\(\alpha_{\mathrm{Cd}^{2+}}\) depende de la concentración de NH 3. Contraste esto con\(\alpha_{\text{Y}^{4-}}\), que depende del pH.
Resolviendo la Ecuación\ ref {9.5} para [Cd 2+] y sustituyendo en Ecuación\ ref {9.4} da
\[K_{f}^{\prime}=K_{f} \times \alpha_{Y^{4-}} = \frac {[\text{CdY}^{2-}]} {\alpha_{\text{Cd}^{2+}} C_\text{Cd} C_\text{EDTA}} \nonumber\]
Debido a que la concentración de NH 3 en un buffer es esencialmente constante, podemos reescribir esta ecuación
para dar una constante de formación condicional,\(K_f^{\prime \prime}\), que da cuenta tanto del pH como de la concentración del agente complejante auxiliar. La Tabla 9.3.3 proporciona valores de\(\alpha_{\text{M}^{2+}}\) para varios iones metálicos cuando NH 3 es el agente complejante.
Curvas de valoración de EDTA complejométricas
Ahora que sabemos algo sobre las propiedades químicas del EDTA, estamos listos para evaluar su utilidad como valorante. Para ello necesitamos conocer la forma de una curva de valoración complejométrica. En el capítulo 9.2 aprendimos que una curva de valoración ácido-base muestra cómo cambia el pH de la titrand a medida que agregamos el valorante. El resultado análogo para una titulación de complejación muestra el cambio en pM, donde M es la concentración del ión metálico, en función del volumen de EDTA. En esta sección aprenderemos a calcular una curva de titulación utilizando los cálculos de equilibrio del Capítulo 6. También aprenderemos a trazar una buena aproximación de cualquier curva de titulación de complejación usando un número limitado de cálculos simples.
pM = —log [M 2+]
Cálculo de la curva de valoración
Calculemos la curva de valoración para 50.0 mL de\(5.00 \times 10^{-3}\) M Cd 2 + usando un valorante de 0.0100 M EDTA. Además, supongamos que el valor está tamponado a un pH de 10 usando un tampón que es 0.0100 M en NH 3.
Debido a que el pH es 10, parte del EDTA está presente en formas distintas a Y4—. Además, EDTA competirá con NH 3 por el Cd 2 +. Para evaluar la curva de titulación, por lo tanto, primero necesitamos calcular la constante de formación condicional para CDy 2—. De la Tabla 9.3.1 y la Tabla 9.3.3 encontramos que\(\alpha_{\text{Y}^{4-}}\) es 0.367 a un pH de 10, y que\(\alpha_{\text{Cd}^{2+}}\) es 0.0881 cuando la concentración de NH 3 es 0.0100 M. Usando estos valores, la constante de formación condicional es
\[K_{f}^{\prime \prime}=K_{f} \times \alpha_{\text{Y}^{4-}} \times \alpha_{\text{Cd}^{2+}}=\left(2.9 \times 10^{16}\right)(0.367)(0.0881)=9.4 \times 10^{14} \nonumber\]
Debido a que\(K_f^{\prime \prime}\) es tan grande, podemos tratar la reacción de titulación
\[\mathrm{Cd}^{2+}(a q)+\mathrm{Y}^{4-}(a q) \longrightarrow \mathrm{CdY}^{2-}(a q) \nonumber\]
como si procediera a su finalización.
La siguiente tarea es determinar el volumen de EDTA necesario para alcanzar el punto de equivalencia. En el punto de equivalencia sabemos que los moles de EDTA añadidos deben ser iguales a los moles de Cd 2 + en nuestra muestra; así
\[\operatorname{mol} \mathrm{EDTA}=M_{\mathrm{EDTA}} \times V_{\mathrm{EDTA}}=M_{\mathrm{Cd}} \times V_{\mathrm{Cd}}=\mathrm{mol} \ \mathrm{Cd}^{2+} \nonumber\]
Sustituyendo en valores conocidos, encontramos que requiere
\[V_{eq}=V_{\mathrm{EDTA}}=\frac{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{EDTA}}}=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{0.0100 \ \mathrm{M}}=25.0 \ \mathrm{mL} \nonumber\]
de EDTA para alcanzar el punto de equivalencia.
Antes del punto de equivalencia, Cd 2+ está presente en exceso y PcD se determina por la concentración de Cd 2 + sin reaccionar. Debido a que no todos los Cd 2 + sin reaccionar son libres —algunos están complejados con NH 3 — debemos dar cuenta de la presencia de NH 3. Por ejemplo, después de agregar 5.0 mL de EDTA, la concentración total de Cd 2 + es
\[C_{\mathrm{Cd}} = \frac {(\text{mol Cd}^{2+})_\text{initial} - (\text{mol EDTA})_\text{added}} {\text{total volume}} = \frac {M_\text{Cd}V_\text{Cd} - M_\text{EDTA}V_\text{EDTA}} {V_\text{Cd} + V_\text{EDTA}} \nonumber\]
\[C_{\mathrm{Cd}}=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})-(0.0100 \ \mathrm{M})(5.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+5.0 \ \mathrm{mL}} \nonumber\]
\[C_{\mathrm{Cd}}=3.64 \times 10^{-3} \ \mathrm{M} \nonumber\]
Para calcular la concentración de Cd 2 + libre utilizamos la Ecuación\ ref {9.5}
\[\left[\mathrm{Cd}^{2+}\right]=\alpha_{\mathrm{Cd}^{2+}} \times C_{\mathrm{Cd}}=(0.0881)\left(3.64 \times 10^{-3} \ \mathrm{M}\right)=3.21 \times 10^{-4} \ \mathrm{M} \nonumber\]
que da un PcD de
\[\mathrm{pCd}=-\log \left[\mathrm{Cd}^{2+}\right]=-\log \left(3.21 \times 10^{-4}\right)=3.49 \nonumber\]
En el punto de equivalencia todo Cd 2 + inicialmente en la titrand ahora está presente como CDy 2—. La concentración de Cd2 +, por lo tanto, está determinada por la disociación del complejo CdY 2—. Primero, calculamos la concentración de CDy 2—.
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(\mathrm{mol} \ \mathrm{Cd}^{2+}\right)_{\mathrm{initial}}}{\text { total volume }} = \frac {M_\text{Cd}V_\text{Cd}} {V_\text{Cd} + V_\text{EDTA}} \nonumber\]
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+25.0 \ \mathrm{mL}}=3.33 \times 10^{-3} \ \mathrm{M} \nonumber\]
A continuación, resolvemos la concentración de Cd 2 + en equilibrio con CdY 2—.
\[K_{\mathrm{f}}^{\prime \prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{C_{\mathrm{Cd}} C_{\mathrm{EDTA}}}=\frac{3.33 \times 10^{-3}-x}{(x)(x)}=9.5 \times 10^{14} \nonumber\]
\[x=C_{\mathrm{Cd}}=1.87 \times 10^{-9} \ \mathrm{M} \nonumber\]
Al calcular que [CdY 2—] en el punto de equivalencia es\(3.33 \times 10^{-3}\) M, asumimos que la reacción entre Cd 2 + y EDTA fue a su finalización. Aquí dejamos que el sistema se relaje de nuevo al equilibrio, aumentando C Cd y C EDTA de 0 a x, y disminuyendo la concentración de CdY 2— por x.
Una vez más, para encontrar la concentración de Cd no complejado debemos dar cuenta de la presencia de NH 3; así
\[\left[\mathrm{Cd}^{2+}\right]=\alpha_{\mathrm{Cd}^{2+}} \times C_{\mathrm{Cd}}=(0.0881)\left(1.87 \times 10^{-9} \ \mathrm{M}\right)=1.64 \times 10^{-10} \ \mathrm{M} \nonumber\]
y PcD es 9.78 en el punto de equivalencia.
Después del punto de equivalencia, EDTA está en exceso y la concentración de Cd 2 + se determina por la disociación del complejo CdY 2—. Primero, calculamos las concentraciones de CdY 2— y de EDTA sin reaccionar. Por ejemplo, después de agregar 30.0 mL de EDTA la concentración de CdY 2— es
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(\mathrm{mol} \mathrm{Cd}^{2+}\right)_{\mathrm{initial}}}{\text { total volume }} = \frac{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{V_{\mathrm{Cd}}+V_{\mathrm{EDTA}}} \nonumber\]
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+30.0 \ \mathrm{mL}}=3.12 \times 10^{-3} \ \mathrm{M} \nonumber\]
y la concentración de EDTA es
\[C_{\mathrm{EDTA}} = \frac {(\text{mol EDTA})_\text{added} - (\text{mol Cd}^{2+})_\text{initial}} {\text{total volume}} = \frac{M_{\mathrm{EDTA}} V_{\mathrm{EDTA}}-M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{V_{\mathrm{Cd}}+V_{\mathrm{EDTA}}} \nonumber\]
\[C_{\text{EDTA}} = \frac {(0.0100 \text{ M})(30.0 \text{ mL}) - (5.00 \times 10^{-3} \text{ M})(50.0 \text{ mL})} {50.0 \text{ mL} + 30.0 \text{ mL}} \nonumber\]
\[C_{\mathrm{EDTA}}=6.25 \times 10^{-4} \ \mathrm{M} \nonumber\]
Sustituyendo en Ecuación\ ref {9.6} y resolviendo [Cd 2 +] da
\[\frac{\left[\mathrm{CdY}^{2-}\right]}{C_{\mathrm{Cd}} C_{\mathrm{EDTA}}} = \frac{3.12 \times 10^{-3} \ \mathrm{M}}{C_{\mathrm{Cd}}\left(6.25 \times 10^{-4} \ \mathrm{M}\right)} = 9.5 \times 10^{14} \nonumber\]
\[C_{\text{Cd}} = 5.27 \times 10^{-15} \text{ M} \nonumber\]
\[ \left[ \text{Cd}^{2+} \right] = \alpha_{\text{Cd}^{2+}} \times C_{\text{Cd}} = (0.0881)(5.27 \times 10^{-15} \text{ M}) = 4.64 \times 10^{-16} \text{ M} \nonumber\]
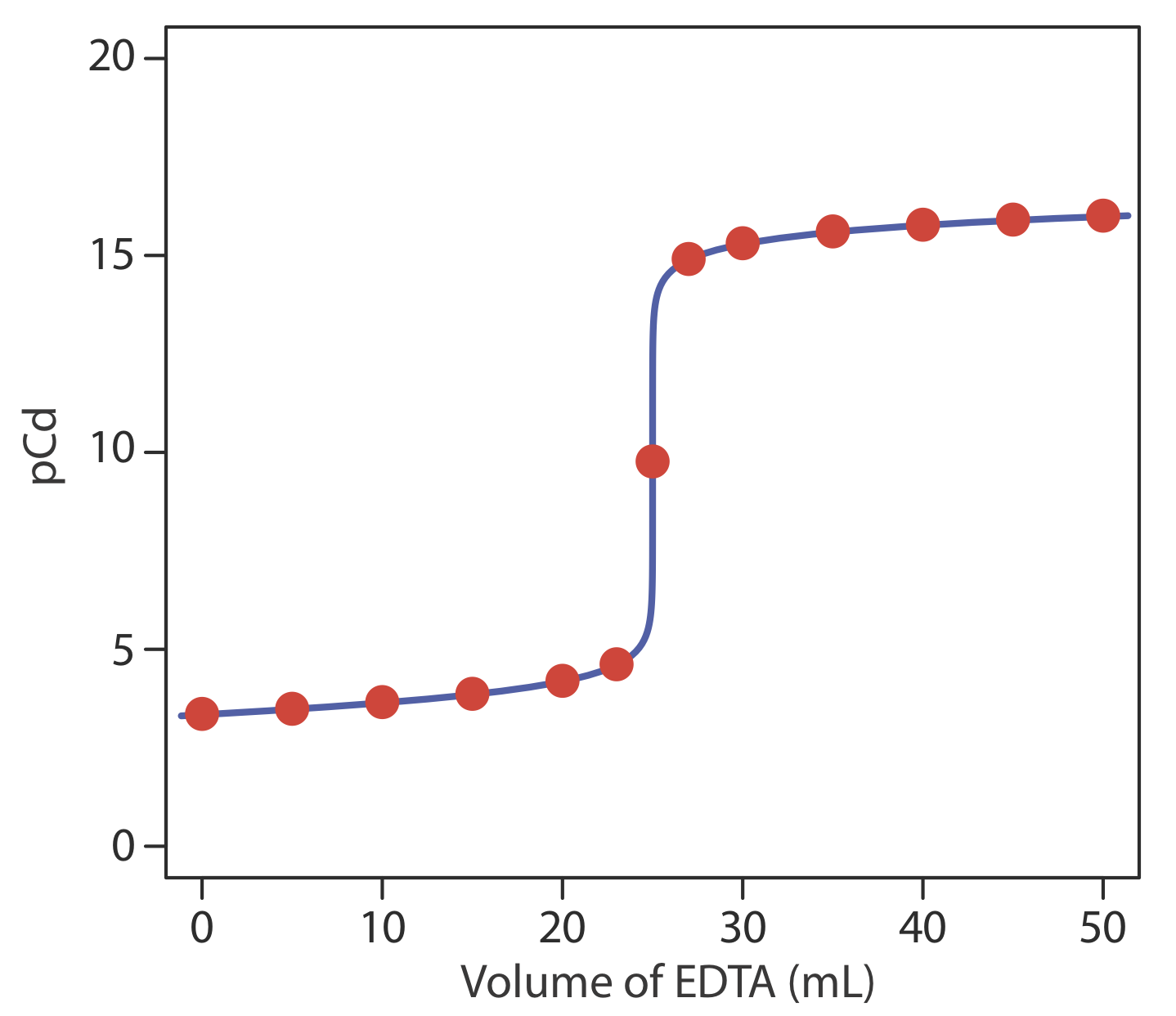
un PcD de 15.33. La Tabla 9.3.4 y la Figura 9.3.3 muestran resultados adicionales para esta valoración.
Después del punto de equilibrio conocemos las concentraciones de equilibrio de CdY 2 - y de EDTA en todas sus formas, C EDTA. Podemos resolver para C Cd usando\(K_f^{\prime \prime}\) y luego calcular [Cd 2 +] usando\(\alpha_{\text{Cd}^{2+}}\). Debido a que utilizamos la misma constante de formación condicional\(K_f^{\prime \prime}\),, para otros cálculos en esta sección, este es el enfoque que se utiliza aquí también. Existe un segundo método para calcular [Cd 2 +] después del punto de equivalencia. Debido a que el cálculo utiliza solo [CDy 2 -] y C EDTA, podemos usar\(K_f^{\prime}\) en lugar de\(K_f^{\prime \prime}\); así
\[\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}}=\alpha_{\mathrm{Y}^{4-}} \times K_{\mathrm{f}} \nonumber\]
\[\frac{3.13 \times 10^{-3} \ \mathrm{M}}{\left[\mathrm{Cd}^{2+}\right]\left(6.25 \times 10^{-4}\right)}=(0.367)\left(2.9 \times 10^{16}\right) \nonumber\]
Resolviendo da [Cd 2 +] =\(4.71 \times 10^{-16}\) M y un PcD de 15.33. Utilizaremos este enfoque cuando aprendamos a bosquejar una curva de titulación complejométrica.
Calcular las curvas de titulación para la titulación de 50.0 mL de\(5.00 \times 10^{-3}\) M Cd 2 + con EDTA 0.0100 M (a) a un pH de 10 y (b) a un pH de 7. Ninguna titulación incluye un agente complejante auxiliar. Compara tus resultados con la Figura 9.3.3 y comenta el efecto del pH en la titulación de Cd 2 + con EDTA.
- Responder
-
Comencemos con los cálculos a un pH de 10 donde parte del EDTA está presente en formas distintas a Y4—. Para evaluar la curva de titulación, por lo tanto, necesitamos la constante de formación condicional para CDy 2—, que, de la Tabla 9.3.2 es\(K_f^{\prime} = 1.1 \times 10^{16}\). Obsérvese que la constante de formación condicional es mayor en ausencia de un agente complejante auxiliar.
El punto de equivalencia de la titulación requiere
\[V_{e q}=V_{\mathrm{EDTA}}=\frac{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{EDTA}}}=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{(0.0100 \ \mathrm{M})}=25.0 \ \mathrm{mL} \nonumber\]
de EDTA.
Antes del punto de equivalencia, Cd 2+ está presente en exceso y PcD se determina por la concentración de Cd 2 + sin reaccionar. Por ejemplo, después de agregar 5.00 mL de EDTA, la concentración total de Cd 2 + es
\[\left[\mathrm{Cd}^{2+}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})-(0.0100 \ \mathrm{M})(5.00 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+5.00 \ \mathrm{mL}} \nonumber\]
lo que da [Cd 2 +] como\(3.64 \times 10^{-3}\) y PcD como 2.43.
En el punto de equivalencia todo Cd 2 + inicialmente en la titrand ahora está presente como CDy 2—. La concentración de Cd2 +, por lo tanto, está determinada por la disociación del complejo CdY 2—. Primero, calculamos la concentración de CDy 2—.
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+25.00 \ \mathrm{mL}}=3.33 \times 10^{-3} \ \mathrm{M} \nonumber\]
A continuación, resolvemos la concentración de Cd 2 + en equilibrio con CdY 2—.
\[K_{f}^{\prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}}=\frac{3.33 \times 10^{-3}-x}{(x)(x)}=1.1 \times 10^{16} \nonumber\]
Resolviendo da [Cd 2 +] como\(5.50 \times 10^{-10}\) M o un PcD de 9.26 en el punto de equivalencia.
Después del punto de equivalencia, EDTA está en exceso y la concentración de Cd 2 + se determina por la disociación del complejo CdY 2—. Primero, calculamos las concentraciones de CdY 2— y de EDTA sin reaccionar. Por ejemplo, después de agregar 30.0 mL de EDTA
\[\left[\mathrm{CdY}^{2-}\right]=\frac{\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+30.00 \ \mathrm{mL}}=3.12 \times 10^{-3} \ \mathrm{M} \nonumber\]
\[C_{\mathrm{EDTA}}=\frac{(0.0100 \ \mathrm{M})(30.00 \ \mathrm{mL})-\left(5.00 \times 10^{-3} \ \mathrm{M}\right)(50.0 \ \mathrm{mL})}{50.0 \ \mathrm{mL}+30.00 \ \mathrm{mL}} \nonumber\]
\[C_{\mathrm{EDTA}}=6.25 \times 10^{-4} \ \mathrm{M} \nonumber\]
Sustituir en la ecuación la constante de formación condicional
\[K_{f}^{\prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}}=\frac{3.12 \times 10^{-3} \ \mathrm{M}}{(\mathrm{x})\left(6.25 \times 10^{-4} \ \mathrm{M}\right)}=1.1 \times 10^{16} \nonumber\]
y resolviendo para [Cd 2 +] da\(4.54 \times 10^{-16}\) M o un PcD de 15.34.
Los cálculos a un pH de 7 son idénticos, excepto que la constante de formación condicional para CdY 2— es\(1.5 \times 10^{13}\) en lugar de\(1.1 \times 10^{16}\). La siguiente tabla resume los resultados de estas dos titulaciones así como los resultados de la Tabla 9.3.4 para la valoración de Cd 2 + a pH 10 en presencia de 0.0100 M NH 3 como agente complejante auxiliar.
Volumen de EDTA (mL)
PcD a pH 10
PcD a pH 10 w/ 0.0100 M NH 3
PcD a pH 7
0 2.30
3.36
2.30
5.00
2.43
3.49
2.43
10.0 2.60
3.66
2.60
15.0 2.81
3.87
2.81
20.0 3.15
4.20
3.15
23.0 3.56
4.62
3.56
25.0 9.26
9.77
7.83
27.0 14.94 14.95 12.08
30.0 15.34 15.33 12.48 35.0 15.61 15.61 12.78 40.0 15.76 15.76 12.95 45.0 15.86 15.86 13.08 50.0 15.94 15.94 13.18 Examinar estos resultados nos permite sacar varias conclusiones. Primero, en ausencia de un agente complejante auxiliar la curva de titulación antes del punto de equivalencia es independiente del pH (compárese las columnas 2 y 4). En segundo lugar, para cualquier pH, la curva de titulación después del punto de equivalencia es la misma independientemente de que esté presente un agente complejante auxiliar (compárese las columnas 2 y 3). En tercer lugar, el mayor cambio en el pH a través del punto de equivalencia ocurre a pH más altos y en ausencia de un agente complejante auxiliar. Por ejemplo, de 23.0 mL a 27.0 mL de EDTA el cambio en PcD es 11.38 a un pH de 10, 10.33 a un pH de 10 en presencia de 0.0100 M NH 3, y 8.52 a un pH de 7.
Dibujar una curva de valoración con EDTA
Para evaluar la relación entre el punto de equivalencia de una titulación y su punto final, necesitamos construir solo una aproximación razonable de la curva de titulación exacta. En esta sección demostramos un método sencillo para esbozar una curva de titulación de complejación. Nuestro objetivo es esbozar la curva de valoración rápidamente, utilizando el menor número posible de cálculos. Vamos a utilizar la titulación de 50.0 mL de\(5.00 \times 10^{-3}\) M Cd 2 + con EDTA 0.0100 M en presencia de 0.0100 M NH 3 para ilustrar nuestro enfoque. Este es el mismo ejemplo que usamos en el desarrollo de los cálculos para una curva de titulación de complejación. Puedes revisar los resultados de ese cálculo en la Tabla 9.3.4 y Figura 9.3.3 .
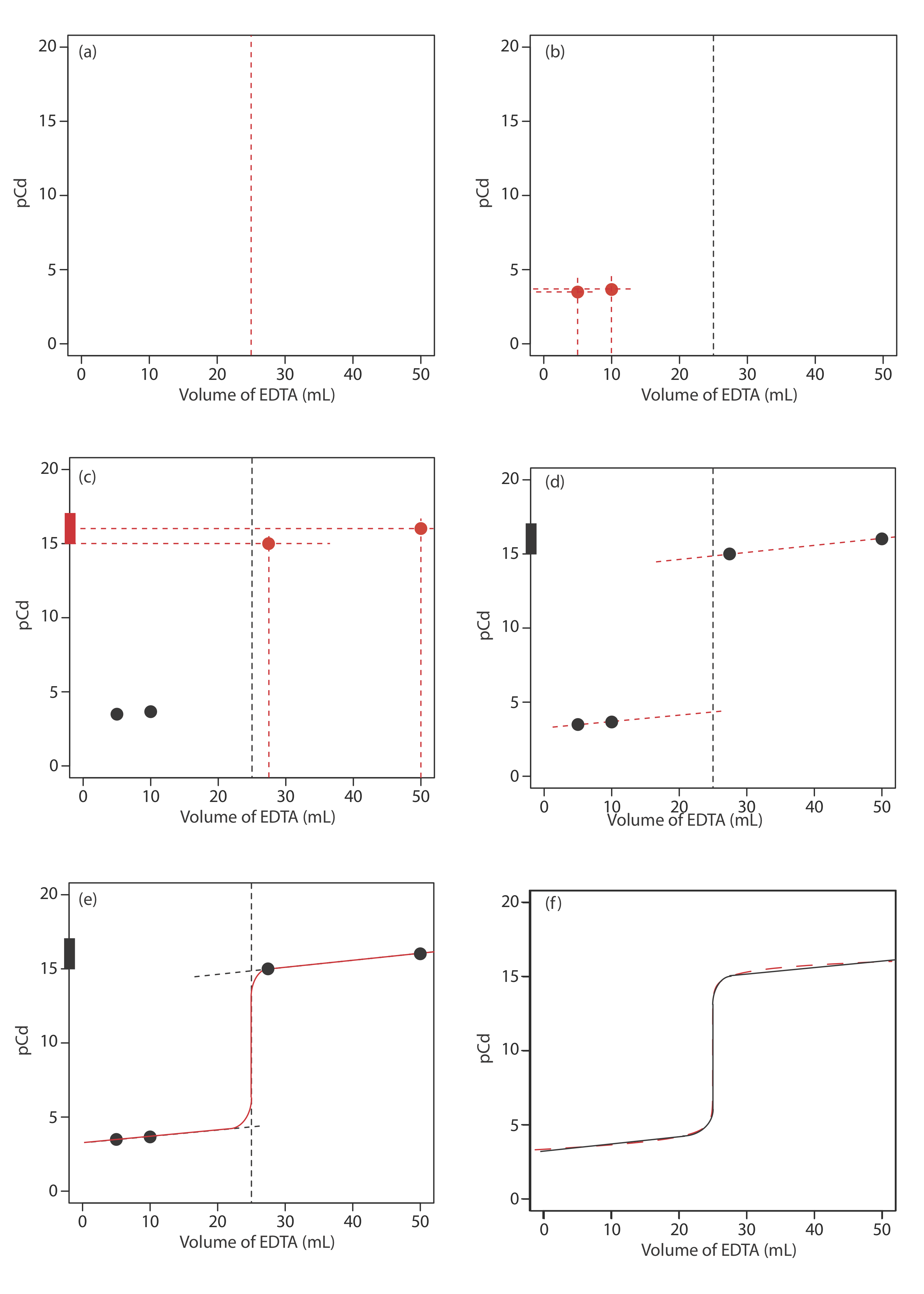
Comenzamos calculando el volumen del punto de equivalencia de la titulación, el cual, como determinamos anteriormente, es de 25.0 mL. A continuación, dibujamos nuestros ejes, colocando PcD en el eje y y el volumen del valorante en el eje x. Para indicar el volumen del punto de equivalencia, dibujamos una línea vertical que cruza el eje x a 25.0 mL de EDTA. La figura 9.3.4 a muestra el resultado del primer paso en nuestro boceto.
Antes del punto de equivalencia, Cd 2 + está presente en exceso y PcD se determina por la concentración de Cd 2 + sin reaccionar. Debido a que no todos los Cd 2 + sin reaccionar son libres —algunos están complejados con NH 3 — debemos dar cuenta de la presencia de NH 3. Los cálculos son sencillos, como vimos antes. La Figura 9.3.4 b muestra la PcD después de agregar 5.00 mL y 10.0 mL de EDTA.
El tercer paso para esbozar nuestra curva de valoración es sumar dos puntos después del punto de equivalencia. Aquí la concentración de Cd 2 + es controlada por la disociación del complejo Cd 2 + —EDTA. Comenzando con la constante de formación condicional
\[K_{f}^{\prime}=\frac{\left[\mathrm{CdY}^{2-}\right]}{\left[\mathrm{Cd}^{2+}\right] C_{\mathrm{EDTA}}} = \alpha_{\text{Y}^{4-}} \times K_{f}=(0.367)\left(2.9 \times 10^{16}\right)=1.1 \times 10^{16} \nonumber\]
tomamos el tronco de cada lado y reorganizamos, llegando a
\[\begin{array}{c}{\log K_{f}^{\prime}=-\log \left[\mathrm{Cd}^{2+}\right]+\log \frac{\left[\mathrm{CdY}^{2-}\right]}{C_{\mathrm{EDTA}}}} \\ {\mathrm{pCd}=\log K_{f}^{\prime}+\log \frac{C_{\mathrm{EDTA}}}{\left[\mathrm{CdY}^{2-}]\right.}}\end{array} \nonumber\]
Recordemos que podemos usar cualquiera de nuestras dos posibles constantes de formación condicional,\(K_f^{\prime}\) o bien\(K_f^{\prime \prime}\), para determinar la composición del sistema en equilibrio.
Obsérvese que después del punto de equivalencia, el título es un tampón de complejación metal-ligando, con PcD determinado por C EDTA y [CdY 2—]. El búfer está en su límite inferior de\(\text{pCd} = \log{K_f^{\prime}} - 1\) cuando
\[\frac{C_{\mathrm{EDTA}}}{\left[\mathrm{CdY}^{2-}\right]} = \frac {(\text{mole EDTA})_\text{added} - (\text{mol Cd}^{2+})_\text{initial}} {(\text{mol Cd}^{2+})_\text{initial}} = \frac {1} {10} \nonumber\]
Haciendo sustituciones adecuadas y resolviendo, encontramos que
\[\frac{M_{\mathrm{EDTA}} V_{\mathrm{EDTA}}-M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{Cd}} V_{\mathrm{Cd}}}=\frac{1}{10} \nonumber\]
\[M_{\mathrm{EDTA}} V_{\mathrm{EDTA}}-M_{\mathrm{Cd}} V_{\mathrm{Cd}}=0.1 \times M_{\mathrm{Cd}} V_{\mathrm{Cd}} \nonumber\]
\[V_{\mathrm{EDTA}}=\frac{1.1 \times M_{\mathrm{Cd}} V_{\mathrm{Cd}}}{M_{\mathrm{EDTA}}}=1.1 \times V_{e q} \nonumber\]
Así, cuando la titulación alcanza el 110% del volumen del punto de equivalencia, PcD es\(\log{K_f^{\prime}} - 1\). Un cálculo similar debería convencerte de que PcD es\(\log{K_f^{\prime}} + 1\) cuando el volumen de EDTA es\(2 \times V_\text{eq}\).
La figura 9.3.4 c muestra el tercer paso en nuestro boceto. Primero, agregamos un diagrama de escalera para el complejo CDy 2—, incluyendo su rango de búfer, usando su\(\log{K_f^{\prime}}\) valor de 16.04. A continuación, sumamos dos puntos, uno para PcD al 110% de V eq (un PcD de 15.04 a 27.5 mL) y uno para PcD al 200% de V eq (un PcD de 16.04 a 50.0 mL).
A continuación, dibujamos una línea recta a través de cada par de puntos, extendiendo cada línea a través de la línea vertical que indica el volumen del punto de equivalencia (Figura 9.3.4 d). Finalmente, completamos nuestro boceto dibujando una curva suave que conecta los tres segmentos de línea recta (Figura 9.3.4 e). Una comparación de nuestro boceto con la curva de titulación exacta (Figura 9.3.4 f) muestra que están muy de acuerdo.
Nuestro tratamiento aquí es general y se aplica a cualquier titulación de complejación usando EDTA como valorante.
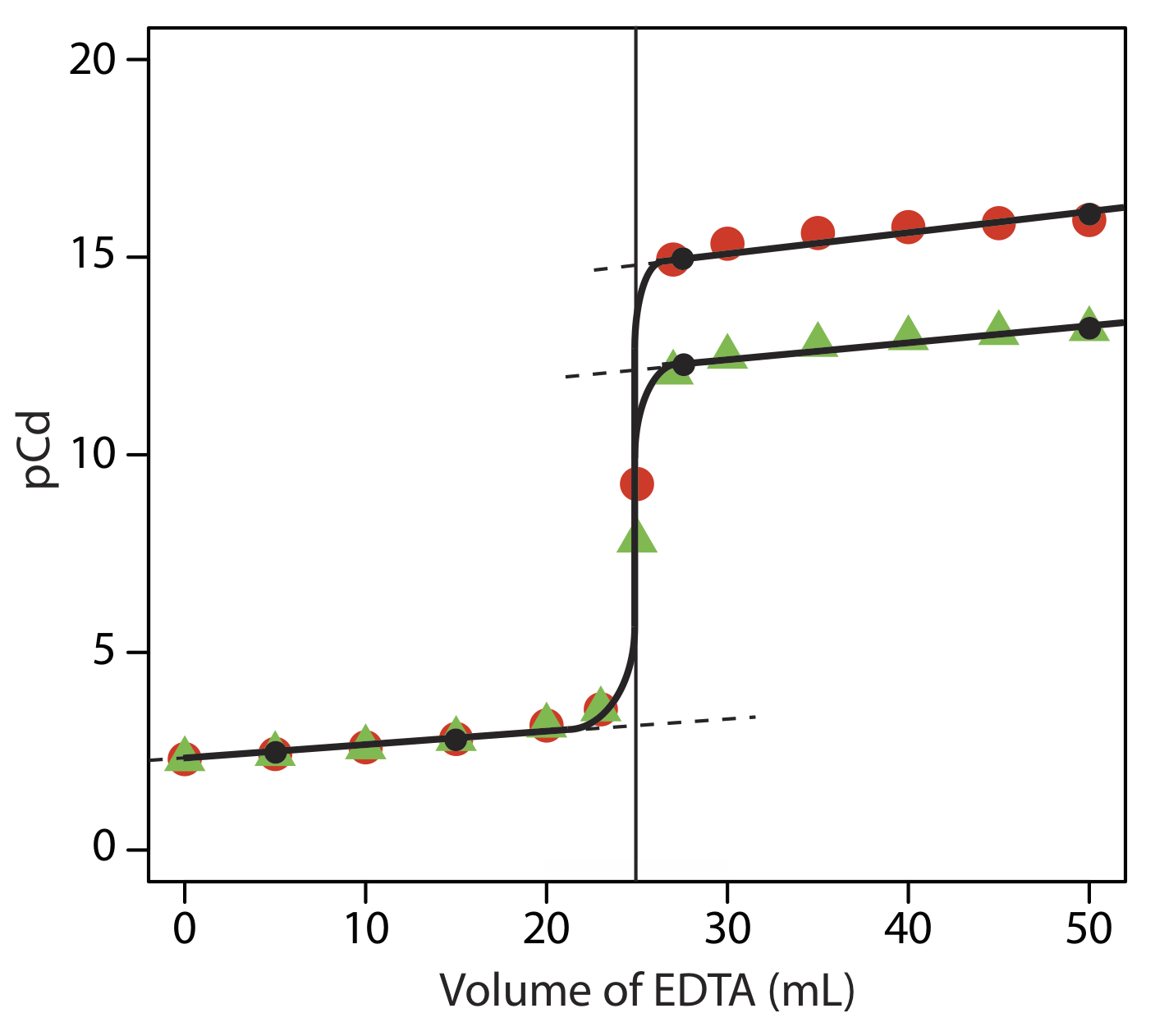
Esbozar curvas de titulación para la titulación de 50.0 mL de\(5.00 \times 10^{-3}\) M Cd 2 + con EDTA 0.0100 M (a) a un pH de 10 y (b) a un pH de 7. Compara tus bocetos con las curvas de valoración calculadas del Ejercicio 9.3.1 .
- Responder
-
La siguiente figura muestra un boceto de las curvas de valoración. Los dos puntos negros antes del punto de equivalencia (V EDTA = 5 mL, PCD= 2.43 y V EDTA = 15 mL, PCD= 2.81) son los mismos para ambos pHs y tomados de los resultados del Ejercicio 9.3.1 . Los dos puntos negros después del punto de equivalencia para un pH de 7 (V EDTA = 27.5 mL, PCD= 12.2 y V EDTA = 50 mL, PCD= 13.2) se trazan usando el\(\log{K_f^{\prime}}\) de 13.2 para CdY 2 -. Los dos puntos después del punto de equivalencia para un pH de 10 (V EDTA = 27.5 mL, PCD= 15.0 y V EDTA = 50 mL, PCD= 16.0) se trazan usando el\(\log{K_f^{\prime}}\) de 16.0 para CdY 2 -. Los puntos en rojo son los cálculos del Ejercicio 9.3.1 para un pH de 10, y los puntos en verde son los cálculos del Ejercicio 9.3.1 para un pH de 7.
Selección y Evaluación del Punto Final
El punto de equivalencia de una titulación de complejación ocurre cuando reaccionamos cantidades estequiométricamente equivalentes del título y el valorante. Como es el caso de una valoración ácido-base, estimamos el punto de equivalencia para una titulación de complejación usando un punto final experimental. Hay una variedad de métodos disponibles para localizar el punto final, incluidos indicadores y sensores que responden a un cambio en las condiciones de la solución.
Encontrar el punto final con un indicador
La mayoría de los indicadores para las titulaciones de complejación son colorantes orgánicos, conocidos como indicadores metalocrómicos, que forman complejos estables con iones metálicos. El indicador, In m —, se agrega a la solución de la titrand donde forma un complejo estable con el ion metálico, MiN n —. A medida que agregamos EDTA reacciona primero con iones metálicos libres, y luego desplaza el indicador de MiN n —.
\[\text{MIn}^{n-}(aq) + \text{Y}^{4-}(aq) \rightarrow \text{MY}^{2-}(aq) + \text{In}^{m-}(aq) \nonumber\]
Si MiN n — e In m — tienen diferentes colores, entonces el cambio de color indica el punto final.
La precisión del punto final de un indicador depende de la resistencia del complejo metal-indicador en relación con la resistencia del complejo metal-EDTA. Si el complejo metal-indicador es demasiado fuerte, el cambio de color ocurre después del punto de equivalencia. Sin embargo, si el complejo metal-indicador es demasiado débil, el punto final ocurre antes de llegar al punto de equivalencia.
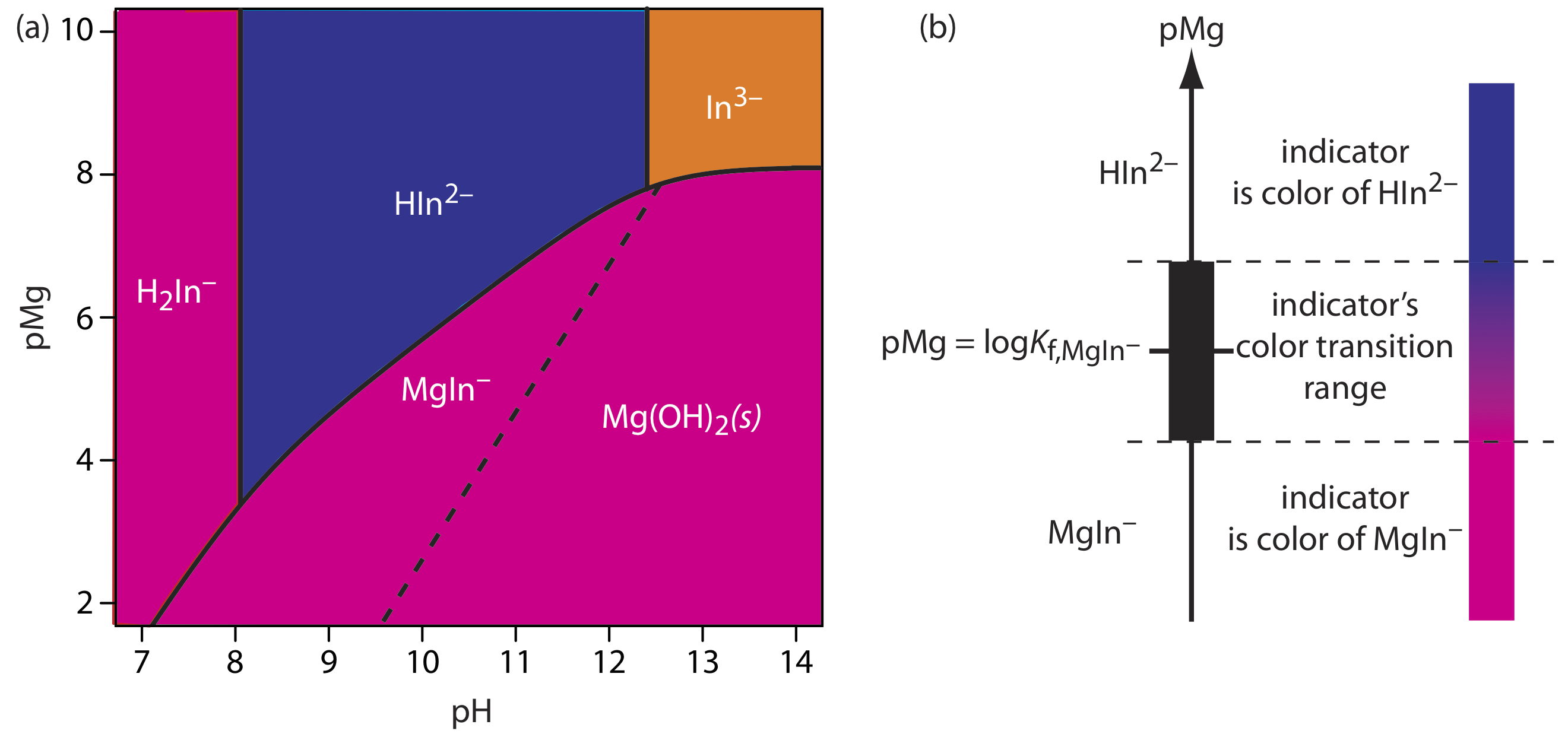
La mayoría de los indicadores metalocrómicos también son ácidos débiles. Una consecuencia de esto es que la constante de formación condicional para el complejo metal-indicador depende del pH de la titrand. Esto proporciona cierto control sobre el error de titulación de un indicador, ya que podemos ajustar la fuerza de un complejo metal-indicador ajustando el pH al que realizamos la titulación. Desafortunadamente, debido a que el indicador es un ácido débil, el color del indicador no complejado también puede cambiar con el pH. La Figura 9.3.5 , por ejemplo, muestra el color del indicador calmagite en función del pH y pMg, donde H 2 In —, HIn 2— e In 3— son formas diferentes del indicador no complejado, y MgIn — es el Mg 2 + —complejo de calmagita. Debido a que el color del complejo metal-indicador de la calmagita es rojo, su uso como indicador metalocrómico tiene un rango de pH práctico de aproximadamente 8.5—11 donde el indicador no complejado, HiN 2—, tiene un color azul.
El cuadro 9.3.5 proporciona ejemplos de indicadores metalocrómicos y los iones metálicos y las condiciones de pH para las que son útiles. Incluso si no existe un indicador adecuado, a menudo es posible completar una titulación de EDTA introduciendo una pequeña cantidad de un complejo de metal secundario-EDTA si el ion metálico secundario forma un complejo más fuerte con el indicador y un complejo más débil con EDTA que el analito. Por ejemplo, la calmagita tiene un punto final pobre al valorar Ca 2 + con EDTA. Agregar una pequeña cantidad de Mg 2 + —EDTA a la titrand da un punto final más nítido. Debido a que Ca 2 + forma un complejo más fuerte con EDTA, desplaza Mg 2 +, que luego forma el complejo Mg 2 + —calmagita de color rojo. En el punto final de la titulación, EDTA desplaza Mg 2 + del complejo Mg 2 + —calmagita, señalando el punto final por la presencia de la forma azul del indicador no complejado.
Encontrar el punto final mediante el monitoreo de la absorbancia
Una limitación importante al usar un indicador metalocrómico es que debemos poder ver el cambio de color del indicador en el punto final. Esto puede ser difícil si la solución ya está coloreada. Por ejemplo, cuando se valora Cu 2 + con EDTA, se usa amoníaco para ajustar el pH del titrand. El\(\text{Cu(NH}_3)_2^{4+}\) complejo intensamente coloreado oscurece el color del indicador, dificultando una determinación precisa del punto final. Otras especies absorbentes presentes dentro de la matriz de muestra también pueden interferir. Esto suele ser un problema a la hora de analizar muestras clínicas, como sangre, o muestras ambientales, como las aguas naturales.
Si al menos una especie en una titulación de complejación absorbe radiación electromagnetica, entonces podemos identificar el punto final monitoreando la absorbancia de la titrand a una longitud de onda cuidadosamente seleccionada. Por ejemplo, podemos identificar el punto final para una titulación de Cu 2 + con EDTA en presencia de NH 3 mediante el monitoreo de la absorbancia del titrand a una longitud de onda de 745 nm, donde el\(\text{Cu(NH}_3)_2^{4+}\) complejo absorbe fuertemente. Al inicio de la titulación la absorbancia se encuentra en un máximo. A medida que añadimos EDTA, sin embargo, la reacción
\[\text{Cu(NH}_3)_4^{2+}(aq) + \text{Y}^{4-} \rightleftharpoons \text{CuY}^{2-}(aq) + 4\text{NH}_3(aq) \nonumber\]
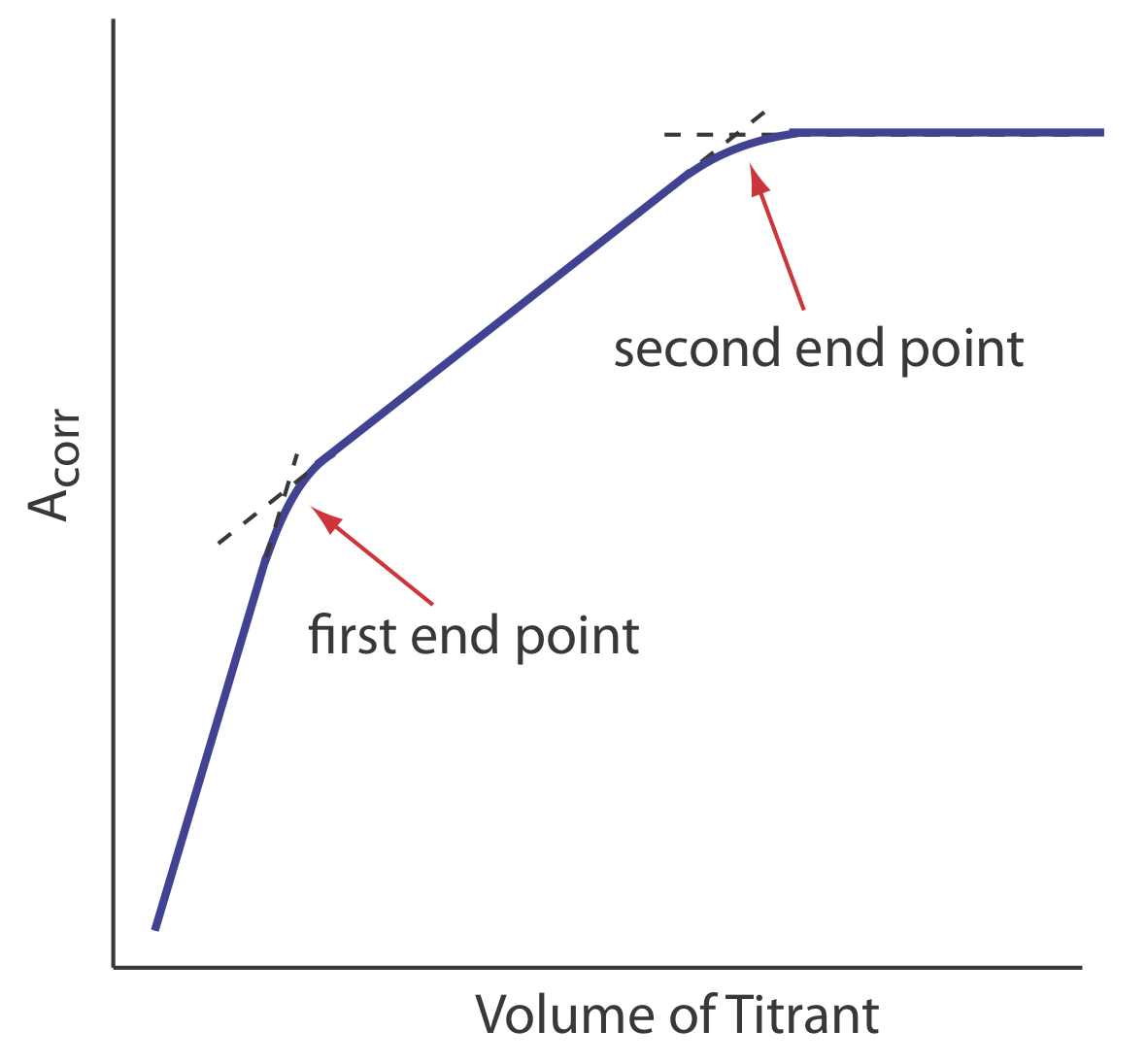
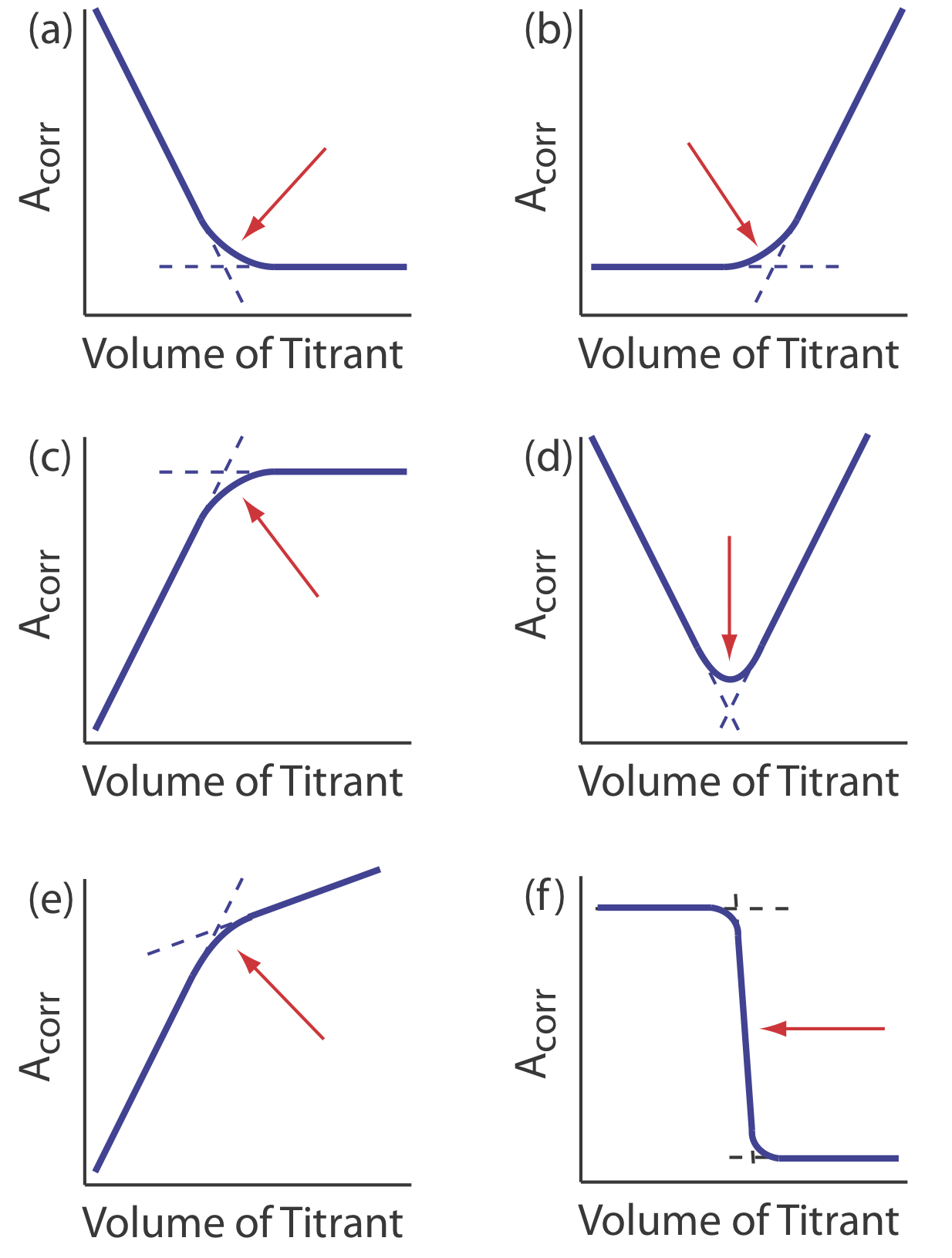
disminuye la concentración de\(\text{Cu(NH}_3)_2^{4+}\) y disminuye la absorbancia hasta alcanzar el punto de equivalencia. Después del punto de equivalencia la absorbancia esencialmente permanece sin cambios. La curva de valoración espectrofotométrica resultante se muestra en la Figura {{template.Index (ID:6)} a. Obsérvese que el eje y de la curva de titulación no es la absorbancia medida, A meas, sino una absorbancia corregida, A corr
\[A_\text{corr} = A_\text{meas} \times \frac {V_\text{EDTA} + V_\text{Cu}} {V_\text{Cu}} \nonumber\]
donde V EDTA y V Cu son, respectivamente, los volúmenes de EDTA y Cu. La corrección de la absorbancia para la dilución de la titrand asegura que la curva de valoración espectrofotométrica consiste en segmentos lineales que podemos extrapolar para encontrar el punto final. Otras curvas de valoración espectrofotométricas comunes se muestran en las Figuras 9.3.6 b-f.
Método Representativo 9.3.1: Determinación de la Dureza del Agua y Aguas Residuales
La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método titrimétrico típico de complejación. Aunque cada método es único, la siguiente descripción de la determinación de la dureza del agua proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en el Método 2340C publicado en Standard Methods for the Examination of Water and Wastewater, 20th Ed., American Public Health Association: Washington, D. C., 1998.
Descripción del Método
La definición operativa de dureza del agua es la concentración total de cationes en una muestra que puede formar un complejo insoluble con jabón. Aunque la mayoría de los iones metálicos divalentes y trivalentes contribuyen a la dureza, los dos iones metálicos más importantes son Ca 2 + y Mg 2 +. La dureza se determina titulando con EDTA a un pH tamponado de 10. La calmagita se utiliza como indicador. La dureza se reporta como mg CaCo 3 /L.
Procedimiento
Seleccionar un volumen de muestra que requiera menos de 15 mL de titulante para mantener el tiempo de análisis por debajo de 5 minutos y, si es necesario, diluir la muestra a 50 mL con agua destilada. Ajustar el pH de la muestra añadiendo 1—2 mL de un tampón pH 10 que contiene una pequeña cantidad de Mg 2 + —EDTA. Agregar 1—2 gotas de indicador y valorar con una solución estándar de EDTA hasta alcanzar el punto final rojo a azul (Figura 9.3.7 ).

Preguntas
1. ¿Por qué la muestra está tamponada a un pH de 10? ¿Qué problemas podría esperar a un pH más alto o a un pH más bajo?
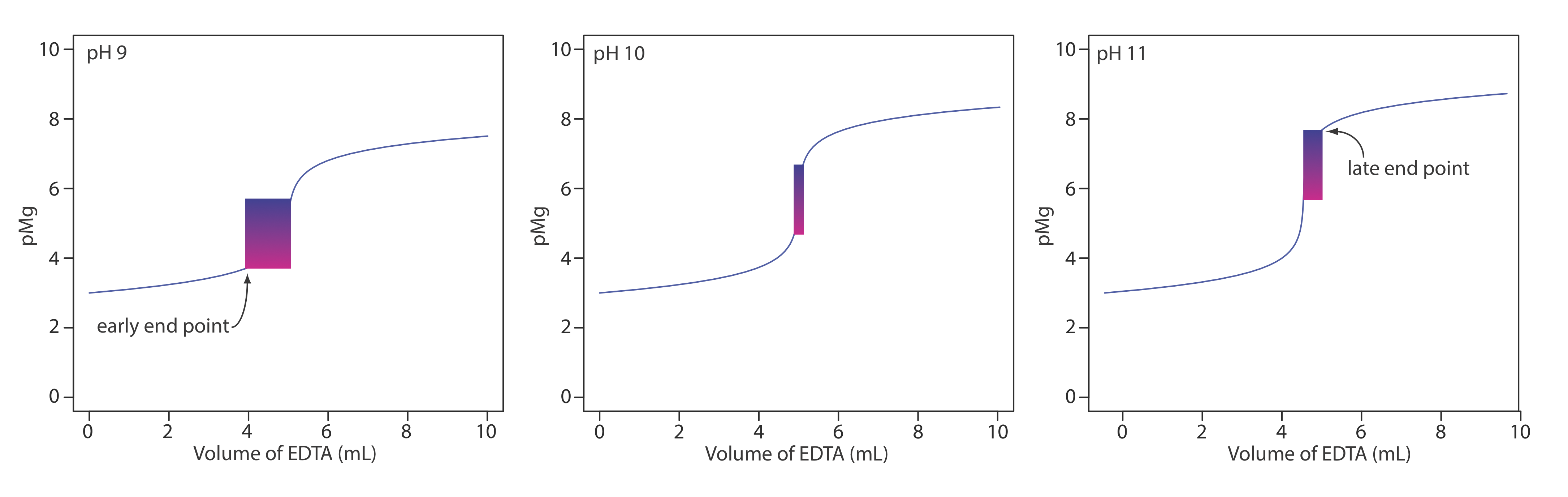
De los dos cationes primarios que contribuyen a la dureza, Mg 2 + forma el complejo más débil con EDTA y es el último catión en reaccionar con el valorante. La calmagita es un indicador útil porque da un punto final distinto al valorar Mg 2 + (ver Tabla 9.3.5 ). Debido a las propiedades ácido-base de la calmagita, el rango de valores de PMg sobre el cual el indicador cambia de color depende del pH de la titrand (Figura 9.3.5 ). La Figura 9.3.8 muestra la curva de titulación para una solución de 50 mL de 10 —3 M Mg 2 + con EDTA 10 —2 M a pH de 9, 10 y 11. Superpuesto en cada curva de titulación se encuentra el rango de condiciones para las cuales el analista promedio observará el punto final. A un pH de 9 es posible un punto final temprano, lo que da como resultado un error determinado negativo. Un punto final tardío y un error determinado positivo son posibles si el pH es 11.
2. ¿Por qué se agrega una pequeña cantidad del complejo Mg 2 + —EDTA al tampón?
El punto final de la titulación es señalado por el indicador calmagite. El punto final del indicador con Mg 2 + es distinto, pero su cambio de color al valorar Ca 2 + no proporciona un buen punto final (consulte la Tabla 9.3.5 ). Si la muestra no contiene ningún Mg 2 + como fuente de dureza, entonces el punto final de la titulación está mal definido, lo que lleva a un resultado inexacto e impreciso. Agregar una pequeña cantidad de Mg 2 + —EDTA al tampón asegura que el título incluya al menos algo de Mg 2 +. Debido a que Ca 2 + forma un complejo más fuerte con EDTA, desplaza Mg 2 + del complejo Mg 2 + —EDTA, liberando el Mg 2 + para unirse con el indicador. Este desplazamiento es estequiométrico, por lo que la concentración total de cationes de dureza permanece inalterada. El desplazamiento por EDTA de Mg 2 + del complejo Mg 2 + —indicador señala el punto final de la titulación.
3. ¿Por qué el procedimiento especifica que la titulación no toma más de 5 minutos?
Una limitación de tiempo sugiere que hay una interferencia cinética controlada, posiblemente derivada de una reacción química competitiva. En este caso la interferencia es la posible precipitación de CaCo 3 a un pH de 10.
Aplicaciones Cuantitativas
Aunque muchas aplicaciones cuantitativas de la titrimetría de complejación han sido reemplazadas por otros métodos analíticos, algunas aplicaciones importantes continúan encontrando relevancia. En la sección revisamos la aplicación general de la titrimetría de complejación con énfasis en aplicaciones a partir del análisis de agua y aguas residuales. Primero, sin embargo, discutimos la selección y estandarización de los titulantes de complejación.
Selección y Estandarización de Titulantes
El EDTA es un valorante versátil que se puede utilizar para analizar prácticamente todos los iones metálicos. Si bien el EDTA es el valorante habitual cuando el título es un ion metálico, no se puede utilizar para valorar aniones, para lo cual Ag + o Hg 2 + son titulantes adecuados.
Las soluciones de EDTA se preparan a partir de su sal disódica soluble, Na 2 H 2 Y•2H 2 O, y se estandarizan valorando contra una solución elaborada a partir del patrón primario CaCo 3. Las soluciones de Ag + y Hg 2 + se preparan utilizando AgnO 3 y Hg (NO 3) 2, ambos estándares secundarios. La estandarización se logra valorando contra una solución preparada a partir de NaCl de grado estándar primario.
Analitos inorgánicos
La titrimetría de complejación continúa siendo catalogada como un método estándar para la determinación de la dureza, Ca 2+, CN — y Cl — en aguas y aguas residuales. La evaluación de la dureza se describió anteriormente en el Método Representativo 9.3.1. La determinación de Ca 2 + se complica por la presencia de Mg 2 +, que también reacciona con EDTA. Para evitar una interferencia el pH se ajusta a 12—13, el cual precipita Mg 2 + como Mg (OH) 2. La valoración con EDTA usando murexide o Eriocromo Azul Negro R como indicador da la concentración de Ca 2 +.
El cianuro se determina en concentraciones mayores a 1 mg/L haciendo la muestra alcalina con NaOH y valorando con una solución estándar de AgnO 3 para formar el\(\text{Ag(CN)}_2^-\) complejo soluble. El punto final se determina utilizando p-dimetilaminobencalrodamina como indicador, con la solución cambiando de color amarillo a salmón en presencia de exceso de Ag +.
El cloruro se determina valorando con Hg (NO 3) 2, formando HgCl 2 (ac). La muestra se acidifica a un pH de 2.3—3.8 y la difenilcarbazona, que forma un complejo coloreado con exceso de Hg 2 +, sirve como indicador. Se agrega el indicador de pH xileno cianol FF para asegurar que el pH esté dentro del rango deseado. La solución inicial es un azul verdoso, y la titulación se lleva a cabo hasta un punto final púrpura.
Cálculos cuantitativos
La relación cuantitativa entre el valorador y el valorante está determinada por la estequiometría de la reacción de titulación. Para una titulación con EDTA, la estequiometría es siempre 1:1.
La concentración de una solución de EDTA se determina estandarizando contra una solución de Ca 2 + preparada usando un estándar primario de CaCo 3. Una muestra de 0.4071 g de CaCo 3 se transfiere a un matraz aforado de 500 ml, se disuelve usando un mínimo de HCl 6 M y se diluye a volumen. Después de transferir una porción de 50.00-mL de esta solución a un matraz Erlenmeyer de 250 mL, el pH se ajusta añadiendo 5 mL de un tampón NH 3 —NH 4 Cl pH 10 que contiene una pequeña cantidad de Mg 2 + —EDTA. Después de agregar calmagita como indicador, la solución se titula con el EDTA, requiriendo 42.63 mL para llegar al punto final. Reportar la concentración molar de EDTA en el titulante.
Solución
El estándar primario de Ca 2+ tiene una concentración de
\[\frac {0.4071 \text{ g CaCO}_3}{0.5000 \text{ L}} \times \frac {1 \text{ mol Ca}^{2+}}{100.09 \text{ g CaCO}_3} = 8.135 \times 10^{-3} \text{ M Ca}^{2+} \nonumber\]
Los moles de Ca 2+ en la titrand es
\[8.135 \times 10^{-3} \text{ M Ca}^{2+} \times 0.05000 \text{ L} = 4.068 \times 10^{-4} \text{ mol Ca}^{2+} \nonumber\]
lo que significa que se utilizan\(4.068 \times 10^{-4}\) moles de EDTA en la titulación. La molaridad del EDTA en el valorante es
\[\frac {4.068 \times 10^{-4} \text{ mol Ca}^{2+}}{0.04263 \text{ L}} = 9.543 \times 10^{-3} \text{ M EDTA} \nonumber\]
Se analiza la dureza de una muestra de 100.0 mL utilizando el procedimiento descrito en el Método Representativo 9.3.1, requiriendo 23.63 mL de EDTA 0.0109 M. Reporte la dureza de la muestra como mg CaCo 3 /L.
- Responder
-
En un análisis de dureza tratamos la muestra como si Ca 2 + fuera el único ion metálico que reacciona con EDTA. Los gramos de Ca 2 + en la muestra, por lo tanto, son
\[(0.0109 \text{ M EDTA})(0.02363 \text{ L}) \times \frac {1 \text{ mol Ca}^{2+}}{\text{mol EDTA}} = 2.58 \times 10^{-4} \text{ mol Ca}^{2+} \nonumber\]
\[2.58 \times 10^{-4} \text{ mol Ca}^{2+} \times \frac {1 \text{ mol CaCO}_3}{\text{mol Ca}^{2+}} \times \frac {100.09 \text{ g CaCO}_3}{\text{mol CaCO}_3} = 0.0258 \text{ g CaCO}_3 \nonumber\]
y la dureza de la muestra es
\[\frac {0.0258 \text{ g CaCO}_3}{0.1000 \text{ L}} \times \frac {1000 \text{ mg}}{\text{g}} = 258 \text{ g CaCO}_3\text{/L} \nonumber\]
Como se muestra en el siguiente ejemplo, podemos extender este cálculo a reacciones de complejación que utilizan otros titulantes.
La concentración de Cl — en una muestra de 100.0-mL de agua de un acuífero de agua dulce se prueba para detectar la invasión de agua de mar valorando con 0.0516 M Hg (NO 3) 2. La muestra se acidifica y se titula hasta el punto final de difenilcarbazona, requiriendo 6.18 mL del valorante. Reportar la concentración de Cl —, en mg/L, en el acuífero.
Solución
La reacción entre Cl — y Hg 2 + produce un complejo metal-ligando de HgCl 2 (ac). Cada mol de Hg 2 + reacciona con 2 moles de Cl —; así
\[\frac {0.0516 \text{ mol Hg(NO}_3)_2}{\text{L}} \times 0.00618 \text{ L} \times \frac {2 \text{ mol Cl}^-}{\text{mol Hg(NO}_3)_2} \times \frac {35.453 \text{ g Cl}^-}{\text{mol Cl}^-} = 0.0226 \text{ g Cl}^- \nonumber\]
están en la muestra. La concentración de Cl — en la muestra es
\[\frac {0.0226 \text{ g Cl}^-}{0.1000 \text{ L}} \times \frac {1000 \text{ mg}}{\text{g}} = 226 \text{ mg/L} \nonumber\]
Una muestra de 0.4482 g de NaCN impuro se titula con AgnO 3 0.1018 M, requiriendo 39.68 mL para llegar al punto final. Reportan la pureza de la muestra como% w/w de NaCN.
- Responder
-
La titulación de CN — con Ag + produce el complejo metal-ligando\(\text{Ag(CN)}_2^-\); así, cada mol de AgnO 3 reacciona con dos moles de NaCN. Los gramos de NaCN en la muestra son
\[(0.1018 \text{ M AgNO}_3)(0.03968 \text{ L}) \times \frac {2 \text{ mol NaCN}}{\text{mol AgNO}_3} \times \frac {49.01 \text{ g NaCN}}{\text{mol NaCN}} = 0.3959 \text{ g NaCN} \nonumber\]
y la pureza de la muestra es
\[\frac {0.3959 \text{ g NaCN}}{0.4482 \text{ g sample}} \times 100 = 88.33 \text{% w/w NaCN} \nonumber\]
Finalmente, son posibles titulaciones complejas que involucran múltiples analitos o retrotitulaciones.
Una aleación de cromel que contiene Ni, Fe y Cr se analiza mediante una titulación de complejación usando EDTA como valorante. Una muestra de 0.7176 g de la aleación se disuelve en HNO 3 y se diluye a 250 mL en un matraz aforado. Una alícuota de 50.00-mL de la muestra, tratada con pirofosfato para enmascarar el Fe y el Cr, requiere 26.14 mL de EDTA 0.05831 M para alcanzar el punto final del mureóxido. Se trata una segunda alícuota de 50.00-mL con hexacetetramina para enmascarar el Cr. La titulación con EDTA 0.05831 M requiere 35.43 mL para alcanzar el punto final del mureóxido. Finalmente, se trata una tercera alícuota de 50.00-mL con 50.00 mL de EDTA 0.05831 M, y se vuelve a valorar al punto final de mureóxido con 6.21 mL de 0.06316 M Cu 2 +. Reporte los porcentajes en peso de Ni, Fe y Cr en la aleación.
Solución
La estequiometría entre EDTA y cada ion metálico es 1:1. Para cada una de las tres titulaciones, por lo tanto, podemos escribir una ecuación que relacione los moles de EDTA con los moles de iones metálicos que se titulan.
valoración 1: mol Ni = mol
Titulación de EDTA 2: mol Ni +mol Fe = mol
Titulación de EDTA 3: mol Ni + mol Fe + mol Cr + mol Cu = mol EDTA
Utilizamos la primera titulación para determinar los moles de Ni en nuestra porción de 50.00-mL de la aleación disuelta. La titulación utiliza
\[\frac {0.05831 \text{ mol EDTA}}{\text{L}} \times 0.02614 \text{ L} = 1.524 \times 10^{-3} \text{ mol EDTA} \nonumber\]
lo que significa que la muestra contiene\(1.524 \times 10^{-3}\) mol de Ni.
Habiendo determinado los moles de EDTA que reaccionan con Ni, utilizamos la segunda titulación para determinar la cantidad de Fe en la muestra. La segunda titulación utiliza
\[\frac {0.05831 \text{ mol EDTA}}{\text{L}} \times 0.03543 \text{ L} = 2.066 \times 10^{-3} \text{ mol EDTA} \nonumber\]
de los cuales se utilizan\(1.524 \times 10^{-3}\) moles para valorar Ni. Esto deja\(5.42 \times 10^{-4}\) mol de EDTA para reaccionar con Fe; así, la muestra contiene\(5.42 \times 10^{-4}\) mol de Fe.
Finalmente, podemos usar la tercera titulación para determinar la cantidad de Cr en la aleación. La tercera titulación utiliza
\[\frac {0.05831 \text{ mol EDTA}}{\text{L}} \times 0.0500 \text{ L} = 3.926 \times 10^{-3} \text{ mol EDTA} \nonumber\]
de los cuales los\(1.524 \times 10^{-3}\) moles se usan para valorar Ni y los\(5.42 \times 10^{-4}\) moles se usan para valorar el Fe. Esto deja\(8.50 \times 10^{-4}\) mol de EDTA para reaccionar con Cu y Cr. La cantidad de EDTA que reacciona con el Cu es
\[\frac {0.06316 \text{ mol Cu}^{2+}}{\text{L}} \times 0.006211 \text{ L} \times \frac {1 \text{ mol EDTA}}{\text{mol Cu}^{2+}} = 3.92 \times 10^{-4} \text{ mol EDTA} \nonumber\]
dejando\(4.58 \times 10^{-4}\) mol de EDTA para reaccionar con Cr. La muestra, por lo tanto, contiene\(4.58 \times 10^{-4}\) mol de Cr.
Habiendo determinado los moles de Ni, Fe y Cr en una porción de 50.00-mL de la aleación disuelta, podemos calcular el% w/w de cada analito en la aleación.
\[\frac {1.524 \times 10^{-3} \text{ mol Ni}}{50.00 \text{ mL}} \times \frac {58.69 \text{ g Ni}}{\text{mol Ni}} = 0.4472 \text{ g Ni} \nonumber\]
\[\frac {0.4472 \text{ g Ni}}{0.7176 \text{ g sample}} \times 100 = 62.32 \text{% w/w Ni} \nonumber\]
\[\frac {5.42 \times 10^{-4} \text{ mol Fe}}{50.00 \text{ mL}} \times \frac {55.845 \text{ g Fe}}{\text{mol Fe}} = 0.151 \text{ g Fe} \nonumber\]
\[\frac {0.151 \text{ g Fe}}{0.7176 \text{ g sample}} \times 100 = 21.0 \text{% w/w Fe} \nonumber\]
\[\frac {4.58 \times 10^{-4} \text{ mol Cr}}{50.00 \text{ mL}} \times \frac {51.996 \text{ g Cr}}{\text{mol Cr}} = 0.119 \text{ g Cr} \nonumber\]
\[\frac {0.119 \text{ g Cr}}{0.7176 \text{ g sample}} \times 100 = 16.6 \text{% w/w Cr} \nonumber\]
Se puede utilizar una titulación de complejación indirecta con EDTA para determinar la concentración de sulfato,\(\text{SO}_4^{2-}\), en una muestra. Se disuelve una muestra de 0.1557 g en agua y cualquier sulfato presente se precipita como BaSO 4 añadiendo Ba (NO 3) 2. Después de filtrar y enjuagar el precipitado, se disuelve en 25.00 mL de EDTA 0.02011 M. El exceso de EDTA se titula con 0.01113 M Mg 2 +, requiriendo 4.23 mL para llegar al punto final. Calcular el% w/w Na 2 SO 4 en la muestra.
- Responder
-
Los moles totales de EDTA utilizados en este análisis son
\[(0.02011 \text{ M EDTA})(0.02500 \text{ L}) = 5.028 \times 10^{-4} \text{ mol EDTA} \nonumber\]
De ello,
\[(0.01113 \text{ M Mg}^{2+})(0.00423 \text{ L}) \times \frac {1 \text{ mol EDTA}}{\text{mol Mg}^{2+}} = 4.708 \times 10^{-5} \text{ mol EDTA} \nonumber\]
se consumen en la valoración posterior con Mg 2 +, lo que significa que
\[5.028 \times 10^{-4} \text{ mol EDTA} - 4.708 \times 10^{-5} \text{ mol EDTA} = 4.557 \times 10^{-4} \text{ mol EDTA} \nonumber\]
reaccionar con el BasO 4. Cada mol de BaSO 4 reacciona con un mol de EDTA; así
\[4.557 \times 10^{-4} \text{ mol EDTA} \times \frac {1 \text{ mol BaSO}_4}{\text{mol EDTA}} \times \frac {1 \text{ mol Na}_2\text{SO}_4}{\text{mol BaSO}_4} \times \frac {142.04 \text{ g Na}_2\text{SO}_4}{\text{mol Na}_2\text{SO}_4} = 0.06473 \text{ g Na}_2\text{SO}_4 \nonumber\]
\[\frac{0.06473 \text{ g Na}_2\text{SO}_4}{0.1557 \text{ g sample}} \times 100 = 41.57 \text{% w/w Na}_2\text{SO}_4 \nonumber\]
Evaluación de Titrimetría de Complexión
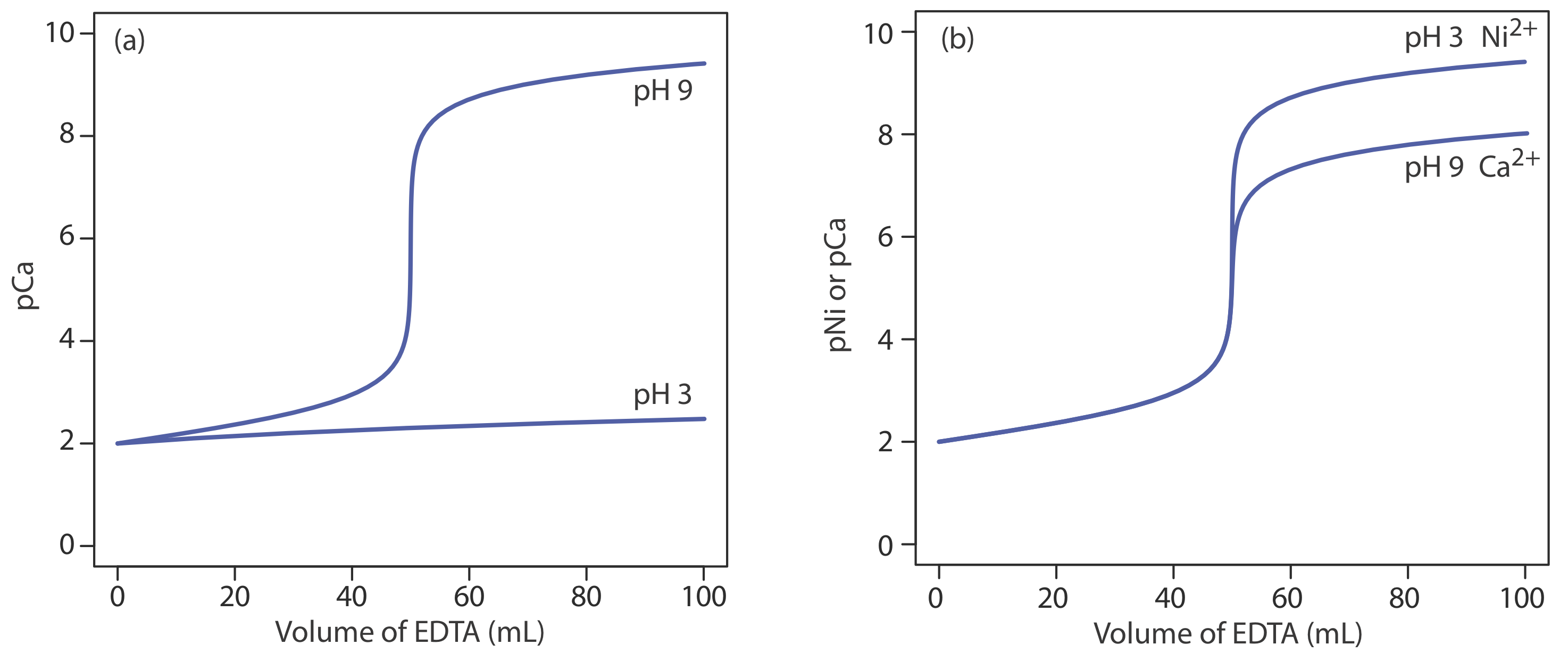
La escala de operaciones, precisión, precisión, sensibilidad, tiempo y costo de una titulación de complejación son similares a las descritas anteriormente para las titulaciones ácido-base. Las titulaciones de complejación, sin embargo, son más selectivas. Aunque el EDTA forma complejos fuertes con la mayoría de los iones metálicos, controlando cuidadosamente el pH de la titrand podemos analizar muestras que contienen dos o más analitos. La razón por la que podemos usar pH para proporcionar selectividad se muestra en la Figura {{template.index (ID:9)} a. Una titulación de Ca 2 + a un pH de 9 tiene una ruptura clara en la curva de titulación porque la constante de formación condicional para CaY 2— de\(2.6 \times 10^9\) es lo suficientemente grande como para asegurar que la reacción de Ca 2 + y EDTA va a su finalización. A un pH de 3, sin embargo, la constante de formación condicional de 1.23 es tan pequeña que muy poco Ca 2 + reacciona con el EDTA. Supongamos que necesitamos analizar una mezcla de Ni 2 + y Ca 2 +. Ambos analitos reaccionan con EDTA, pero sus constantes de formación condicional difieren significativamente. Si ajustamos el pH a 3 podemos valorar Ni 2 + con EDTA sin valorar Ca 2 + (Figura {{Template.index (ID:9)}} b). Cuando se completa la titulación, ajustamos el pH del titrand a 9 y valoramos el Ca 2 + con EDTA.
Una valoración espectrofotométrica es un enfoque particularmente útil para analizar una mezcla de analitos. Por ejemplo, como se muestra en la Figura 9.3.10 , podemos determinar la concentración de dos iones metálicos si existe una diferencia entre la absorbancia de los dos complejos metal-ligando.