9.6: Problemas
- Page ID
- 75402
Algunos de los problemas que siguen requieren una o más constantes de equilibrio o potenciales de estado estándar. Para su comodidad, aquí hay hipervínculos a los apéndices que contienen estas constantes:
Apéndice 10: Productos de solubilidad
Apéndice 11: Constantes de disociación ácida
1. Calcular o esbozar curvas de valoración para las siguientes titulaciones ácido-base.
(a) 25.0 mL de NaOH 0.100 M con HCl 0.0500 M
b) 50,0 mL de HCOOH 0.0500 M con NaOH 0.100 M
(c) 50,0 mL de NH 3 0.100 M con HCl 0.100 M
d) 50,0 mL de etilendiamina 0.0500 M con HCl 0.100 M
(e) 50,0 mL de ácido cítrico 0.0400 M con NaOH 0.120 M
f) 50.0 mL de 0.0400 M H 3 PO 4 con NaOH 0.120 M
2. Localizar el (los) punto (s) de equivalencia para cada curva de titulación en el problema 1 y, cuando sea factible, calcular el pH en el punto de equivalencia. ¿Cuál es la relación estequiométrica entre los moles de ácido y los moles de base para cada uno de estos puntos de equivalencia?
3. Sugerir un indicador visual apropiado para cada una de las titulaciones en el problema 1.
4. Para esbozar la curva de valoración para un ácido débil aproximamos el pH al 10% del volumen del punto de equivalencia como p K a — 1, y el pH al 90% del volumen del punto de equivalencia como p K a + 1. Demostrar que estos supuestos son razonables.
5. El ácido tartárico, H 2 C 4 H 4 O 6, es un ácido diprótico débil con una p K a1 de 3.0 y una p K a2 de 4.4. Supongamos que tiene una muestra de ácido tartárico impuro (pureza > 80%), y que planea determinar su pureza valorando con una solución de NaOH 0.1 M usando un indicador para señalar el punto final. Describa cómo llevará a cabo el análisis, prestando especial atención a la cantidad de muestra a utilizar, el rango de pH deseado para el indicador y cómo calculará el% w/w de ácido tartárico. Suponga que su bureta tiene una capacidad máxima de 50 mL.
6. Los siguientes datos para la titulación de un ácido débil monoprótico con una base fuerte se recolectaron mediante un valorador automático. Prepare curvas de valoración normal, primera derivada, segunda derivada y Gran plot para estos datos, y localice el punto de equivalencia para cada una.
| volumen de NaOH (mL) | pH | volumen de NaOH (mL) | pH |
|---|---|---|---|
|
0.25 |
3.0 | 49.95 | 7.8 |
|
0.86 |
3.2 | 49.97 | 8.0 |
|
1.63 |
3.4 | 49.98 | 8.2 |
|
2.72 |
3.6 | 49.99 | 8.4 |
|
4.29 |
3.8 | 50.00 | 8.7 |
|
6.54 |
4.0 | 50.01 | 9.1 |
|
9.67 |
4.2 | 50.02 | 9.4 |
| 13.79 | 4.4 | 50.04 | 9.6 |
| 18.83 | 4.6 | 50.06 | 9.8 |
| 24.47 | 4.8 | 50.10 | 10.0 |
| 30.15 | 5.0 | 50.16 | 10.2 |
| 35.33 | 5.2 | 50.25 | 10.4 |
| 39.62 | 5.4 | 50.40 | 10.6 |
| 42.91 | 5.6 | 50.63 | 10.8 |
| 45.28 | 5.8 | 51.01 | 11.0 |
| 46.91 | 6.0 | 51.61 | 11.2 |
| 48.01 | 6.2 | 52.58 | 11.4 |
| 48.72 | 6.4 | 54.15 | 11.6 |
| 49.19 | 6.6 | 56.73 | 11.8 |
| 49.48 | 6.8 | 61.11 | 12.0 |
| 49.67 | 7.0 | 68.83 | 12.2 |
| 49.79 | 7.2 | 83.54 | 12.4 |
| 49.87 | 7.4 | 116.14 | 12.6 |
| 49.92 | 7.6 |
7. Schwartz publicó los siguientes datos simulados para la valoración de una solución\(1.02 \times 10^{-4}\) M de un ácido débil monoprótico (p K a = 8.16) con NaOH\(1.004 \times 10^{-3}\) M [Schwartz, L. M. J. Chem. Educ. 1992, 69, 879—883]. La simulación supone que se usa una pipeta de 50 mL para transferir una porción de la solución de ácido débil al recipiente de titulación. Una calibración de la pipeta muestra que entrega un volumen de sólo 49.94 mL. Preparar curvas de valoración normal, primera derivada, segunda derivada y Gran plot para estos datos, y determinar el punto de equivalencia para cada uno. ¿Cómo se comparan estos puntos de equivalencia con el punto de equivalencia esperado? Comentar sobre la utilidad de cada curva de titulación para el análisis de soluciones muy diluidas de ácidos muy débiles.
| mL de NaOH | pH | mL de NaOH | pH |
|---|---|---|---|
|
0.03 |
6.212 |
4.79 |
8.858 |
|
0.09 |
6.504 | 4.99 | 8.926 |
|
0.29 |
6.936 | 5.21 |
8.994 |
|
0.72 |
7.367 | 5.41 | 9.056 |
| 1.06 | 7.567 | 5.61 | 9.118 |
| 1.32 | 7.685 | 5.85 | 9.180 |
| 1.53 | 7.776 | 6.05 | 9.231 |
| 1.76 | 7.863 | 6.28 | 9.283 |
| 1.97 | 7.938 | 6.47 | 9.327 |
| 2.18 | 8.009 | 6.71 | 9.374 |
| 2.38 | 8.077 | 6.92 | 9.414 |
| 2.60 | 8.146 | 7.15 | 9.451 |
| 2.79 | 8.208 | 7.36 | 9.484 |
| 3.01 | 8.273 | 7.56 | 9.514 |
| 3.19 | 8.332 | 7.79 | 9.545 |
| 3.41 | 8.398 | 7.99 | 9.572 |
| 3.60 | 8.458 | 8.21 | 9.599 |
| 3.80 | 8.521 | 8.44 | 9.624 |
| 3.99 | 8.584 | 8.64 | 9.645 |
| 4.18 | 8.650 | 8.84 | 9.666 |
| 4.40 | 8.720 | 9.07 | 9.688 |
| 4.57 | 8.784 | 9.27 | 9.706 |
8. Calcular o bosquejar la curva de titulación para una solución de 50.0 mL de un ácido débil monoprótico 0.100 M (p K a = 8.0) con base fuerte 0.1 M en un solvente no acuoso con K s =\(10^{-20}\). Se puede suponer que el cambio en el disolvente no afecta a los ácidos débiles p K a. Compare su curva de valoración con la curva de valoración cuando el agua es el disolvente.
9. Se sigue espectrofotométricamente la titulación de una mezcla de p-nitrofenol (p K a = 7.0) y m-nitrofenol (p K a = 8.3). Ninguno de los ácidos absorbe a una longitud de onda de 545 nm, pero sus respectivas bases conjugadas sí absorben a esta longitud de onda. El ion m-nitrofenolato tiene una mayor absorbancia que una solución equimolar del ion p-nitrofenolato. Esbozar la curva de valoración espectrofotométrica para una mezcla de 50.00-mL compuesta por p-nitrofenol 0.0500 M y m-nitrofenol 0.0500 M con NaOH 0.100 M. Compara tu resultado con las curvas de valoración potenciométrica esperadas.
10. Se realiza un análisis cuantitativo para anilina (C 6 H 5 NH 2, K b =\(3.94 \times 10^{-10}\)) mediante titulación ácido-base utilizando ácido acético glacial como disolvente y HClO 4 como valorante. Un volumen conocido de muestra que contiene 3—4 mmol de anilina se transfiere a un matraz Erlenmeyer de 250 ml y se diluye a aproximadamente 75 mL con ácido acético glacial. Se agregan dos gotas de un indicador de violeta de metilo, y la solución se titula con HClO 4 0.1000 M previamente estandarizado (preparado en ácido acético glacial usando HClO4 anhidro) hasta alcanzar el punto final. Los resultados se reportan como partes por millón de anilina.
(a) Explique por qué esta titulación se realiza utilizando ácido acético glacial como disolvente en lugar de usar agua.
(b) Un problema con el uso de ácido acético glacial como disolvente es su coeficiente relativamente alto de expansión térmica de 0.11%/o C. Por ejemplo, 100.00 mL de ácido acético glacial a 25 o C ocupa 100.22 mL a 27 o C. ¿Cuál es el efecto sobre la concentración reportada de anilina si la estandarización de HClO 4 se realiza a una temperatura que es menor que la para el análisis de lo desconocido?
c) El procedimiento contempla una muestra que contenga 3—4 mililitros de anilina. ¿Por qué es necesario este requisito?
Algunos de los problemas que siguen requieren una o más constantes de equilibrio o potenciales de estado estándar. Para su comodidad, aquí hay hipervínculos a los apéndices que contienen estas constantes:
Apéndice 10: Productos de solubilidad
Apéndice 11: Constantes de disociación ácida
11. Usando un diagrama de escalera, explique por qué la presencia de CO 2 disuelto conduce a un error determinado para la estandarización de NaOH si el pH del punto final está entre 6—10, pero no un error determinado si el pH del punto final es menor que 6.
12. La acidez de una muestra de agua se determina valorando a pH de punto final fijo de 3.7 y 8.3, proporcionando la primera una medida de la concentración de ácido fuerte y la segunda una medida de las concentraciones combinadas de ácido fuerte y ácido débil. Dibuje una curva de valoración para una mezcla de HCl 0.10 M y H 2 CO 3 0.10 M con base fuerte 0.20 M, y utilícela para justificar la elección de estos puntos finales.
13. El ácido etilendiaminotetraacético, H 4 Y, es un ácido débil con constantes sucesivas de disociación ácida de 0.010,\(2.19 \times 10^{-3}\),\(6.92 \times 10^{-7}\), y\(5.75 \times 10^{-11}\). La siguiente figura muestra una curva de titulación para H 4 Y con NaOH. ¿Cuál es la relación estequiométrica entre H 4 Y y NaOH en el punto de equivalencia marcado con la flecha roja?
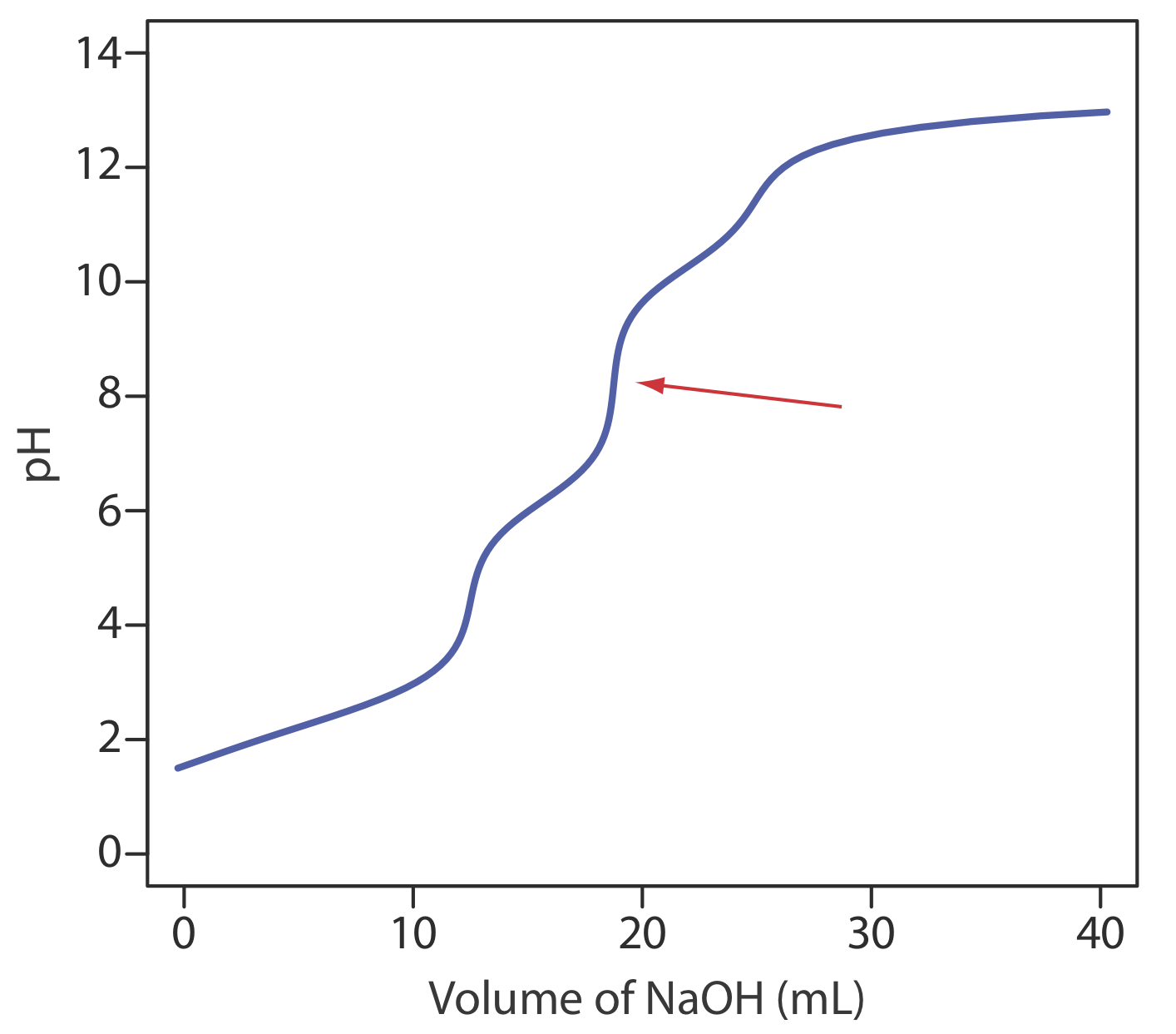
14. Se ha descrito un método de Gran plot para el análisis cuantitativo de una mezcla que consiste en un ácido fuerte y un ácido débil monoprótico [(a) Boiani, J. A. J. Chem. Educ. 1986, 63, 724—726; b) Castillo, C. A.; Jaramillo, A. J. Chem. Educ. 1989, 66, 341]. Una mezcla de 50.00-mL de HCl y CH 3 COOH se transfiere a un matraz Erlenmeyer y se valora usando una pipeta digital para agregar alícuotas sucesivas de 1.00-mL de NaOH 0.09186 M. El progreso de la titulación es monitoreado registrando el pH después de cada adición de valorante. Utilizando los dos trabajos enumerados anteriormente como referencia, se prepara una gráfica Gran para los siguientes datos y se determinan las concentraciones de HCl y CH 3 COOH.
| mL de NaOH | pH | mL de NaOH | pH | mL de NaOH | pH |
|---|---|---|---|---|---|
|
1.00 |
1.83 |
24.00 |
4.45 |
47.00 |
12.14 |
|
2.00 |
1.86 |
25.00 |
4.53 |
48.00 |
12.17 |
|
3.00 |
1.89 |
26.00 |
4.61 |
49.00 |
12.20 |
|
4.00 |
1.92 |
27.00 |
4.69 |
50.00 |
12.23 |
|
5.00 |
1.95 |
28.00 |
4.76 |
51.00 |
12.26 |
|
6.00 |
1.99 |
29.00 |
4.84 |
52.00 |
12.28 |
|
7.00 |
2.03 |
30.00 |
4.93 |
53.00 |
12.30 |
|
8.00 |
2.10 |
31.00 |
5.02 |
54.00 |
12.32 |
|
9.00 |
2.18 |
32.00 |
5.13 |
55.00 |
12.34 |
|
10.00 |
2.31 | 33.00 |
5.23 |
56.00 |
12.36 |
| 11.00 | 2.51 | 34.00 |
5.37 |
57.00 |
12.38 |
| 12.00 | 2.81 | 35.00 |
5.52 |
58.00 |
12.39 |
| 13.00 | 3.16 | 36.00 |
5.75 |
59.00 |
12.40 |
| 14.00 | 3.36 | 37.00 |
6.14 |
60.00 |
12.42 |
| 15.00 | 3.54 | 38.00 |
10.30 |
61.00 | 12.43 |
| 16.00 | 3.69 | 39.00 | 11.31 | 62.00 | 12.44 |
| 17.00 | 3.81 | 40.00 | 11.58 | 63.00 | 12.45 |
| 18.00 | 3.93 | 41.00 | 11.74 | 64.00 | 12.47 |
| 19.00 | 4.02 | 42.00 | 11.85 | 65.00 | 12.48 |
| 20.00 | 4.14 | 43.00 | 11.93 | 66.00 | 12.49 |
| 21.00 | 4.22 | 44.00 | 12.00 | 67.00 | 12.50 |
| 22.00 | 4.30 | 45.00 | 12.05 | 68.00 | 12.51 |
| 23.00 | 4.38 | 46.00 | 12.10 | 69.00 | 12.52 |
15. Explique por qué no es posible que una muestra de agua tenga simultáneamente OH —y\(\text{HCO}_3^-\) como fuentes de alcalinidad—.
16. Para cada una de las muestras a—e, determinar las fuentes de alcalinidad (OH —,\(\text{HCO}_3^-\),\(\text{CO}_3^{2-}\)) y sus respectivas concentraciones en partes por millón En cada caso se titula una muestra de 25.00-mL con HCl 0.1198 M a los puntos finales de verde de bromocresol y fenolftaleína.
| muestra | volumen de HCl (mL) a fenolftaleína punto final | volumen de HCl (mL) al punto final del verde de bromocresol |
|---|---|---|
| a | 21.36 | 21.38 |
| b | 5.67 | 21.13 |
| c | 0.00 | 14.28 |
| d | 17.12 | 34.26 |
| e | 21.36 | 25.69 |
17. Una muestra puede contener cualquiera de los siguientes: HCl, NaOH, H 3 PO 4\(\text{H}_2\text{PO}_4^-\),\(\text{HPO}_4^{2-}\), o\(\text{PO}_4^{3-}\). La composición de una muestra se determina valorando una porción de 25.00 mL con HCl 0.1198 M o NaOH 0.1198 M a la fenolftaleína y a los puntos finales de naranja de metilo. Para cada una de las siguientes muestras, determinar qué especies están presentes y sus respectivas concentraciones molares.
| muestra | titulante | volumen (mL) a fenoftaleína punto final | volumen (mL) a naranja de metilo punto final |
|---|---|---|---|
| a | HCl | 11.54 | 35.29 |
| b | NaOH | 19.79 | 9.89 |
| c | HCl | 22.76 | 22.78 |
| d | NaOH | 39.42 | 17.48 |
18. La proteína en una muestra de 1.2846-g de un cereal de avena se determina mediante un análisis de Kjeldahl. La muestra se digiere con H 2 SO 4, la solución resultante se basifica con NaOH y el NH 3 se destila en 50.00 mL de HCl 0.09552 M. El exceso de HCl se vuelve a valorar usando 37.84 mL de NaOH 0.05992 M. Dado que las proteínas en los granos tienen un promedio de 17.54% w/w de N, reportan el% w/w de proteína en la muestra.
19. La concentración de SO 2 en el aire se determina burbujeando una muestra de aire a través de una trampa que contiene H 2 O 2. La oxidación de SO 2 por H 2 O 2 da como resultado la formación de H 2 SO 4, que luego se determina valorando con NaOH. En un análisis típico, se pasa una muestra de aire a través de la trampa de peróxido a una velocidad de 12.5 L/min durante 60 min y se requirió 10.08 mL de NaOH 0.0244 M para alcanzar el punto final de fenolftaleína. Calcular el μL/L SO 2 en la muestra de aire. La densidad de SO 2 a la temperatura de la muestra de aire es de 2.86 mg/mL.
20. La concentración de CO 2 en el aire se determina mediante una valoración indirecta ácido-base. Se burbujea una muestra de aire a través de una solución que contiene un exceso de Ba (OH) 2, precipitando BaCo 3. El exceso de Ba (OH) 2 se vuelve a valorar con HCl. En un análisis típico se burbujea una muestra de aire de 3.5 l a través de 50.00 mL de 0.0200 M Ba (OH) 2. La valoración posterior con HCl 0.0316 M requiere 38.58 mL para alcanzar el punto final. Determinar las ppm de CO 2 en la muestra de aire dado que la densidad de CO 2 a la temperatura de la muestra es de 1.98 g/L.
Algunos de los problemas que siguen requieren una o más constantes de equilibrio o potenciales de estado estándar. Para su comodidad, aquí hay hipervínculos a los apéndices que contienen estas constantes:
Apéndice 10: Productos de solubilidad
Apéndice 11: Constantes de disociación ácida
21. La pureza de una preparación sintética de metiletilcetona, C 4 H 8 O, se determina haciéndola reaccionar con clorhidrato de hidroxilamina, liberando HCl (ver reacción en la Tabla 9.2.7). En un análisis típico se diluye una muestra de 3.00-mL a 50.00 mL y se trata con un exceso de clorhidrato de hidroxilamina. El HCl liberado se valora con NaOH 0.9989 M, requiriendo 32.68 mL para llegar al punto final. Reportan el porcentaje de pureza de la muestra dado que la densidad de metiletilcetona es de 0.805 g/mL.
22. Las grasas animales y los aceites vegetales son triésteres formados a partir de la reacción entre glicerol (1,2,3-propanotriol) y tres ácidos grasos de cadena larga. Uno de los métodos utilizados para caracterizar una grasa o un aceite es la determinación de su número de saponificación. Cuando se trata con KOH acuoso hirviendo, un éster saponifica en el alcohol parental y ácidos grasos (como iones carboxilato). El número de saponificación es el número de miligramos de KOH requeridos para saponificar 1.000 gramos de la grasa o el aceite. En un análisis típico se agrega una muestra de 2.085-g de mantequilla a 25.00 mL de KOH 0.5131 M. Una vez completada la saponificación, el exceso de KOH se vuelve a titular con 10.26 mL de HCl 0.5000 M. ¿Cuál es el número de saponificación para esta muestra de mantequilla?
23. Una muestra de 250.0-mg de un ácido orgánico débil se disuelve en un solvente apropiado y se titula con NaOH 0.0556 M, requiriendo 32.58 mL para llegar al punto final. Determinar el peso equivalente del compuesto.
24. La siguiente figura muestra una curva de titulación potenciométrica para una muestra de 0.4300-g de un aminoácido purificado que se disolvió en 50.00 mL de agua y se tituló con NaOH 0.1036 M. Identificar el aminoácido a partir de las posibilidades enumeradas en la tabla.
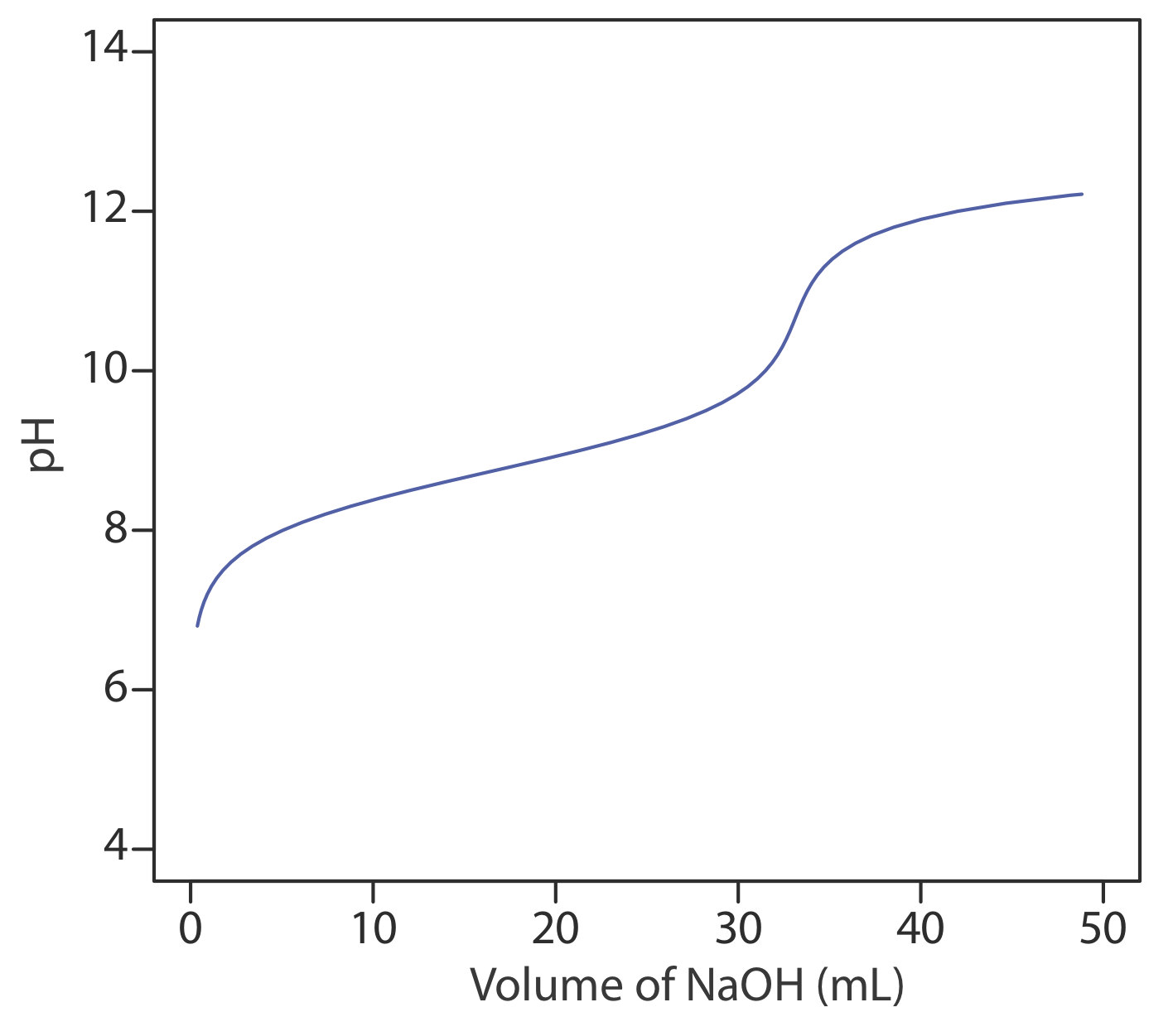
| aminoácido | peso de la fórmula (g/mol) | K a |
|---|---|---|
| alanina | 89.1 | \(1.35 \times 10^{-10}\) |
| glicina | 75.1 | \(1.67 \times 10^{-10}\) |
| metionina | 149.2 | \(8.9 \times 10^{-10}\) |
| taurina | 125.2 | \(1.8 \times 10^{-9}\) |
| asparagina | 150 | \(1.9 \times 10^{-9}\) |
| leucina | 131.2 | \(1.79 \times 10^{-10}\) |
| fenilalanina | 166.2 | \(4.9 \times 10^{-10}\) |
| valina | 117.2 | \(1.91 \times 10^{-10}\) |
25. Mediante su curva de titulación, se determina la constante de disociación ácida para el ácido débil en el problema 9.6.
26. ¿En qué parte de la escala de operaciones pertenecen las técnicas de microtitulación discutidas en el Capítulo 9.7?
27. Se puede usar una titulación ácido-base para determinar el peso equivalente de un analito, pero no puede usarse para determinar su peso de fórmula. Explique por qué.
28. La soda de lavado comercial es aproximadamente del 30— 40% w/w Na 2 CO 3. Un procedimiento para el análisis cuantitativo de la soda de lavado contiene las siguientes instrucciones:
Transfiera una muestra de aproximadamente 4 g de la soda de lavado a un matraz aforado de 250 ml. Disolver la muestra en aproximadamente 100 mL de H 2 O y luego diluir hasta la marca. Usando una pipeta, transferir una alícuota de 25 mL de esta solución a un matraz Erlenmeyer de 125 mL y agregar 25-mL de H 2 O y 2 gotas de indicador verde de bromocresol. Titular la muestra con HCl 0.1 M hasta el punto final del indicador.
¿Qué modificaciones, en su caso, son necesarias si se quiere adaptar este procedimiento para evaluar la pureza del Na 2 CO 3 comercial que es > 98% puro?
29. Una variedad de errores sistemáticos y aleatorios son posibles al estandarizar una solución de NaOH contra el ácido débil primario estándar de ftalato de potasio (KHP). Identificar, con justificación, si las siguientes son fuentes de error sistemático o error aleatorio, o si no afectan al error. Si el error es sistemático, entonces indique si la molaridad determinada experimentalmente para el NaOH es demasiado alta o demasiado baja. La reacción de estandarización es
\[\text{C}_8\text{H}_5\text{O}_4^-(aq) + \text{OH}^-(aq) \rightarrow \text{C}_8\text{H}_4\text{O}_4^-(aq) + \text{H}_2\text{O}(l) \nonumber\]
(a) La balanza utilizada para pesar KHP no está correctamente calibrada y siempre lee 0.15 g demasiado bajo.
b) El indicador para la titulación cambia de color entre un pH de 3—4.
c) Una burbuja de aire, que se aloja en la punta de la bureta al inicio del análisis, se desaloja durante la titulación.
(d) Las muestras de KHP se pesan en matraces Erlenmeyer separados, pero el saldo se alquitranó solo para el primer matraz.
(e) El KHP no se seca antes de ser utilizado.
f) El NaOH no se seca antes de ser utilizado.
(g) El procedimiento establece que la muestra de KHP debe disolverse en 25 mL de agua, pero accidentalmente se disuelve en 35 mL de agua.
30. La concentración de ácido o-ftálico en un disolvente orgánico, tal como n-butanol, se determina mediante una titulación ácido-base usando NaOH acuoso como valorante. A medida que se agrega el valorante, el ácido o-ftálico se extrae en la solución acuosa donde reacciona con el valorante. El valorante se agrega lentamente para permitir el tiempo suficiente para que se lleve a cabo la extracción.
a) ¿Qué tipo de error espera si la titulación se lleva a cabo con demasiada rapidez?
b) Proponer un método alternativo de titulación ácido-base que permita una determinación más rápida de la concentración de ácido o-ftálico en n-butanol.
Algunos de los problemas que siguen requieren una o más constantes de equilibrio o potenciales de estado estándar. Para su comodidad, aquí hay hipervínculos a los apéndices que contienen estas constantes:
Apéndice 10: Productos de solubilidad
Apéndice 11: Constantes de disociación ácida
31. Calcular o bosquejar curvas de titulación para 50.0 mL de 0.100 Mg 2 + con EDTA 0.100 M a un pH de 7 y 10. Localice el punto de equivalencia para cada curva de titulación.
32. Calcular o bosquejar curvas de titulación para 25.0 mL de 0.0500 M Cu 2 + con EDTA 0.025 M a un pH de 10 y en presencia de 10 —3 M y 10 —1 M NH 3. Localice el punto de equivalencia para cada curva de titulación.
33. Esbozar la curva de valoración espectrofotométrica para la valoración de una mezcla de\(5.00 \times 10^{-3}\) M Bi 3 + y\(5.00 \times 10^{-3}\) M Cu 2 + con EDTA 0.0100 M. Supongamos que solo el complejo Cu 2 + —EDTA absorbe a la longitud de onda seleccionada.
34. La titulación con EDTA de mezclas de Ca 2 + y Mg 2 + se puede seguir termométricamente porque la formación del complejo Ca 2 + —EDTA es exotérmica y la formación del complejo Mg 2 + —EDTA es endotérmica. Dibuje la curva de valoración termométrica para una mezcla de\(5.00 \times 10^{-3}\) M Ca 2 + y\(5.00 \times 10^{-3}\) M Mg 2 + usando EDTA 0.0100 M como valorante. Los calores de formación para CaY 2— y MgY 2— son, respectivamente, —23.9 kJ/mol y 23.0 kJ/mol.
35. El EDTA es un miembro de una clase de ligandos de aminocarboxilato que forman complejos 1:1 muy estables con iones metálicos. La siguiente tabla proporciona los valores de log K f para los complejos de seis de dichos ligandos con Ca 2 + y Mg 2 +. ¿Qué ligando es la mejor opción para una valoración directa de Ca 2 + en presencia de Mg 2 +?
| ligando | Mg2+ | Ca2+ |
|---|---|---|
| EDTA: ácido etilendiaminotetraacético | 8.7 | 10.7 |
| HEDTA: Ácido N-hidroxietilendiametriacético | 7.0 | 8.0 |
| EEDTA: ácido etileterdiaminatetraacético | 8.3 | 10.0 |
| EGTA: ácido etilenoglicol-bis (\(\beta\)-aminoetiléter) -N, N'-tetraacético | 5.4 | 10.9 |
| DTPA: ácido dietilenetriaminpentaacético | 9.0 | 107 |
| CyDTA: ácido cicloeanodiaminatetraacético | 10.3 | 12.3 |
36. La cantidad de calcio en los fluidos fisiológicos se determina mediante una titulación complejométrica con EDTA. En uno de esos análisis se basifica una muestra de 0.100 mL de un suero sanguíneo mediante la adición de 2 gotas de NaOH y se titula con EDTA 0.00119 M, requiriendo 0.268 mL para llegar al punto final. Reportar la concentración de calcio en la muestra como miligramos Ca por 100 mL.
37. Después de retirar las membranas de una cáscara de huevo, la cáscara se seca y su masa se registra como 5.613 g. La cáscara de huevo se transfiere a un vaso de precipitados de 250 ml y se disuelve en 25 mL de HCl 6 M. Después de filtrar, la solución que contiene la cáscara de huevo disuelta se diluye a 250 mL en un matraz aforado. Se coloca una alícuota de 10.00 ml en un matraz Erlenmeyer de 125 ml y se tamponó a un pH de 10. La titulación con EDTA 0.04988 M requiere 44.11 mL para llegar al punto final. Determinar la cantidad de calcio en la cáscara de huevo como %w/w CaCo 3.
38. La concentración de cianuro, CN —, en un baño de galvanoplastia de cobre se determina mediante una titulación complejométrica usando Ag + como valorante, formando el\(\text{Ag(CN)}_2^-\) complejo soluble. En un análisis típico, una muestra de 5.00 mL de un baño de galvanoplastia se transfiere a un matraz Erlenmeyer de 250 mL, y se trata con 100 mL de H 2 O, 5 mL de NaOH al 20% p/v y 5 mL de KI al 10% p/v. La muestra se titula con AgnO 3 0.1012 M, requiriendo 27.36 mL para alcanzar el punto final como lo señala la formación de un precipitado amarillo de AgI. Reportar la concentración de cianuro como partes por millón de NaCN.
39. Antes de la introducción del EDTA, la mayoría de las titulaciones de complejación usaban Ag + o CN, como valorante. El análisis para Cd 2 +, por ejemplo, se realizó indirectamente agregando un exceso de KCN para formar\(\text{Cd(CN)}_4^{2-}\), y retrotitulando el exceso de CN — con Ag +, formando\(\text{Ag(CN)}_2^-\). En uno de esos análisis se disuelve una muestra de 0.3000-g de un mineral y se trata con 20.00 mL de KCN 0.5000 M. El exceso de CN — requiere 13.98 mL de 0.1518 M AgnO 3 para llegar al punto final. Determinar el% w/w de Cd en el mineral.
40. Las soluciones que contienen Fe 3 + y Al 3 + se analizan selectivamente para Fe 3 + mediante tamponamiento a pH 2 y titulación con EDTA. Luego se eleva el pH de la solución a 5 y se agrega un exceso de EDTA, dando como resultado la formación del complejo Al 3 + —EDTA. El exceso de EDTA es retrotitulado usando una solución estándar de Fe 3 +, proporcionando un análisis indirecto para Al 3 +.
(a) A un pH de 2, verificar que la formación del complejo Fe 3 + —EDTA sea favorable, y que la formación del complejo Al 3 + —EDTA no sea favorable.
(b) Una alícuota de 50.00-mL de una muestra que contiene Fe 3 + y Al 3 + se transfiere a un matraz Erlenmeyer de 250 mL y se tampola a un pH de 2. Se agrega una pequeña cantidad de ácido salicílico, formando el complejo soluble de Fe 3 + —ácido salicílico de color rojo. La solución se titula con EDTA 0.05002 M, requiriendo 24.82 mL para alcanzar el punto final como lo indica la desaparición del color rojo del complejo Fe 3 + —ácido salicílico. La solución se tampona a un pH de 5 y se añaden 50.00 mL de EDTA 0.05002 M. Después de asegurar que la formación del complejo Al 3 + —EDTA es completa, el exceso de EDTA se vuelve a titular con 0.04109 M Fe 3 +, requiriendo 17.84 mL para alcanzar el punto final como lo señala la reaparición del Fe 3 + — de color rojo complejo de ácido salicílico. Reportan las concentraciones molares de Fe 3 + y A l3 + en la muestra.
Algunos de los problemas que siguen requieren una o más constantes de equilibrio o potenciales de estado estándar. Para su comodidad, aquí hay hipervínculos a los apéndices que contienen estas constantes:
Apéndice 10: Productos de solubilidad
Apéndice 11: Constantes de disociación ácida
41. Prada y sus colegas describieron un método indirecto para determinar el sulfato en muestras naturales, como agua de mar y efluentes industriales [Prada, S.; Guekezian, M.; Suarez-Iha, M. E. V. Anal. Chim. Acta 1996, 329, 197—202]. El método consiste en tres etapas: precipitar el sulfato como PbSO 4; disolver el PbSO 4 en una solución amónica de EDTA en exceso para formar el complejo PBy 2— soluble; y titulación del exceso de EDTA con una solución estándar de Mg 2 +. Se conocen las siguientes reacciones y constantes de equilibrio
\[\text{PbSO}_4(s) \rightleftharpoons \text{Pb}^{2+}(aq) + \text{SO}_4^{2-}(aq) \quad K_\text{sp} = 1.6 \times 10^{-8} \nonumber\]
\[\text{Pb}^{2+}(aq) + \text{Y}^{4-}(aq) \rightleftharpoons \text{PbY}^{2-}(aq) \quad K_\text{f} = 1.1 \times 10^{18} \nonumber\]
\[\text{Mg}^{2+}(aq) + \text{Y}^{4-}(aq) \rightleftharpoons \text{MgY}^{2-}(aq) \quad K_\text{f} = 4.9 \times 10^{8} \nonumber\]
\[\text{Zn}^{2+}(aq) + \text{Y}^{4-}(aq) \rightleftharpoons \text{ZnY}^{2-}(aq) \quad K_\text{f} = 3.2 \times 10^{16} \nonumber\]
a) Verificar que un precipitado de PbSO 4 se disuelva en una solución de Y 4—.
(b) Sporek propuso un método similar utilizando Zn 2 + como valorante y encontró que la precisión frecuentemente era pobre [Sporek, K. F. Anal. Chem. 1958, 30, 1030—1032]. Una explicación es que Zn 2 + podría reaccionar con el complejo PbY 2—, formando ZnY 2—. Demuestre que esto podría ser un problema al usar Zn 2 + como valorante, pero que no es un problema al usar Mg 2 + como valorante. ¿Tal desplazamiento de Pb 2 + por Zn 2 + conduciría al reporte de demasiado o muy poco sulfato?
(c) En un análisis típico, se lleva una muestra de 25.00 mL de un efluente industrial mediante el procedimiento utilizando 50.00 mL de EDTA 0.05000 M. Titular el exceso de EDTA requiere 12.42 mL de 0.1000 M Mg 2 +. Reportar la concentración molar de\(\text{SO}_4^{2-}\) en la muestra de efluente.
42. El Cuadro 9.3.1 proporciona valores para la fracción de EDTA presente como Y 4—,\(\alpha_{\text{Y}^{4-}}\). Los valores de\(\alpha_{\text{Y}^{4-}}\) se calculan usando la ecuación
\[\alpha_{\text{Y}^{4-}} = \frac{[\text{Y}^{4-}]}{C_\text{EDTA}} \nonumber\]
donde [Y 4-] es la concentración del EDTA completamente desprotonado y C EDTA es la concentración total de EDTA en todas sus formas
\[C_\text{EDTA} = [\text{H}_6\text{Y}^{2+}]+[\text{H}_5\text{Y}^{+}]+[\text{H}_4\text{Y}]+ [\text{H}_3\text{Y}^{-}] + [\text{H}_2\text{Y}^{2-}] + [\text{H}_\text{Y}^{3-}] + [\text{Y}^{4-}] \nonumber\]
\[\text{H}_6\text{Y}^{2+} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_5\text{Y}^{+}(aq) \quad K_\text{a1} \nonumber\]
\[\text{H}_5\text{Y}^{+} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_4\text{Y}(aq) \quad K_\text{a2} \nonumber\]
\[\text{H}_4\text{Y} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_3\text{Y}^{-}(aq) \quad K_\text{a3} \nonumber\]
\[\text{H}_3\text{Y}^{-} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_2\text{Y}^{2-}(aq) \quad K_\text{a4} \nonumber\]
\[\text{H}_2\text{Y}^{2-} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}\text{Y}^{3-}(aq) \quad K_\text{a5} \nonumber\]
\[\text{H}\text{Y}^{2-} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{Y}^{4-}(aq) \quad K_\text{a6} \nonumber\]
para demostrar que
\[\alpha_{\text{Y}^{4-}} = \frac{K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4}K_\text{a5}K_\text{a6}}{d} \nonumber\]
donde
\[d = [\text{H}_3\text{O}^+]^6 + [\text{H}_3\text{O}^+]^5K_\text{a1} + [\text{H}_3\text{O}^+]^4K_\text{a1}K_\text{a2} + [\text{H}_3\text{O}^+]^3K_\text{a1}K_\text{a2}K_\text{a3} + [\text{H}_3\text{O}^+]^2K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4} + [\text{H}_3\text{O}^+]K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4}K_\text{a5} + K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4}K_\text{a5}K_\text{a6} \nonumber\]
43. Calcular o esbozar las curvas de valoración para las siguientes reacciones de valoración redox a 25 o C. Supongamos que el analito inicialmente está presente a una concentración de 0.0100 M y que se toma una muestra de 25.0 mL para su análisis. El valorante, que es la especie audaz en cada reacción, tiene una concentración de 0.0100 M.
(a) V 2+ (aq) + Ce 4 + (aq)\(\rightarrow\) V 3+ (aq) + Ce 3 + (aq)
(b) Sn 2 + (aq) + 2 Ce 4 + (aq)\(\rightarrow\) Sn 4 + (aq) +2Ce 3 + (aq)
(c) 5Fe 2 + (aq) +\(\mathbf{MnO}_\mathbf{4}^\mathbf{-}\) (aq) + (aq) + 8H + (aq)\(\rightarrow\) 5Fe 3 + (aq) + Mn 2 + (aq) +4H 2 O (l) a un pH de 1
44. ¿Cuál es el punto de equivalencia para cada titulación en el problema 43?
45. Sugerir un indicador apropiado para cada titulación en el problema 43.
46. El contenido de hierro de un mineral se determina mediante una titulación redox que utiliza K 2 Cr 2 O 7 como valorante. Una muestra del mineral se disuelve en HCl concentrado usando Sn 2 + para acelerar su disolución reduciendo Fe 3 + a Fe 2 +. Después de disolver la muestra, Fe 2 + y cualquier exceso de Sn 2 + se oxidan a Fe 3 + y Sn 4 + usando\(\text{MnO}_4^-\). Luego, el hierro se reduce cuidadosamente a Fe 2 + agregando un exceso de 2—3 gotas de Sn 2 +. Se agrega una solución de HgCl 2 y, si se forma un precipitado blanco de Hg 2 Cl 2, el análisis se continúa valorando con K 2 Cr 2 O 7. La muestra se descarta sin completar el análisis si no se forma un precipitado de Hg 2 Cl 2 o si se forma un precipitado gris (debido a Hg).
(a) Explique por qué la muestra se descarta si no se forma un precipitado blanco de Hg 2 Cl 2 o si se forma un precipitado gris.
b) ¿Se introduce un error determinado si el analista olvida agregar Sn 2 + en el paso donde se disuelve el mineral de hierro?
c) ¿Se introduce un error determinado si el hierro no se oxida cuantitativamente de nuevo a Fe 3 + por el\(\text{MnO}_4^-\)?
47. La cantidad de Cr 3 + en una sal inorgánica se determina mediante una titulación redox. Una porción de muestra que contiene aproximadamente 0.25 g de Cr 3 + se pesa con precisión y se disuelve en 50 mL de H 2 O. El Cr 3 + se oxida\(\text{Cr}_2\text{O}_7^{2-}\) añadiendo 20 mL de AgnO 3 0.1 M, que sirve como catalizador, y 50 mL de 10% p/v (NH 4) 2 S 2 O 8, que sirve como agente oxidante. Una vez completada la reacción, la solución resultante se hierve durante 20 minutos para destruir el exceso\(\text{S}_2\text{O}_8^{2-}\), se enfría a temperatura ambiente y se diluye a 250 mL en un matraz aforado. Una porción de 50 ml de la solución resultante se transfiere a un matraz Erlenmeyer, se trata con 50 mL de una solución estándar de Fe 2 +, y se acidifica con 200 mL de H 1 M 2 SO 4, reduciendo el\(\text{Cr}_2\text{O}_7^{2-}\) a Cr 3 +. El exceso de Fe 2 + se determina luego mediante una retrotitulación con una solución estándar de K 2 Cr 2 O 7 usando un indicador apropiado. Los resultados se reportan como %w/w Cr 3 +.
a) Hay varios lugares en el procedimiento donde se especifica el volumen de un reactivo (ver texto en cursiva). Cuál de estas mediciones se debe realizar utilizando una pipeta volumétrica.
(b) El exceso de peroxidisulfato,\(\text{S}_2\text{O}_8^{2-}\) se destruye hirviendo la solución. ¿Cuál es el efecto sobre el% w/w reportado de Cr 3 + si alguna de las no\(\text{S}_2\text{O}_8^{2-}\) se destruye durante este paso?
(c) Las soluciones de Fe 2 + experimentan una lenta oxidación de aire a Fe 3 +. ¿Cuál es el efecto sobre el% p/p reportado de Cr 3 + si la solución estándar de Fe 2 + se permite inadvertidamente oxidarse parcialmente?
48. La concentración exacta de H 2 O 2 en una solución que es nominalmente 6% p/v H 2 O 2 se determina mediante una valoración redox utilizando\(\text{MnO}_4^-\) como valorante. Una alícuota de 25 ml de la muestra se transfiere a un matraz aforado de 250 ml y se diluye a volumen con agua destilada. Se agrega una alícuota de 25 mL de la muestra diluida a un matraz Erlenmeyer, se diluye con 200 mL de agua destilada, y se acidifica con 20 mL de 25% v/v H 2 SO 4. La solución resultante se titula con una solución estándar de KMnO 4 hasta que persiste un color rosado tenue por 30 s. Los resultados se reportan como% p/v H 2 O 2.
(a) Muchas soluciones comercialmente disponibles de H 2 O 2 contienen un estabilizador inorgánico u orgánico para evitar la autodescomposición del peróxido a H 2 O y O 2. ¿Qué efecto tiene la presencia de este estabilizador sobre el% p/v reportado H 2 O 2 si también reacciona con\(\text{MnO}_4^-\)?
b) El agua destilada de laboratorio a menudo contiene trazas de material orgánico disuelto con el que pueden reaccionar\(\text{MnO}_4^-\). Describir un método sencillo para corregir esta interferencia potencial.
(c) Qué modificaciones al procedimiento, en su caso, son necesarias si la muestra tiene una concentración nominal de 30% p/v H 2 O 2.
49. La cantidad de hierro en un meteorito se determina mediante una valoración redox utilizando KMnO 4 como valorante. Una muestra de 0.4185 g se disuelve en ácido y el Fe 3+ liberado se reduce cuantitativamente a Fe 2+ usando un reductor Walden. La titulación con 0.02500 M KMnO 4 requiere 41.27 mL para llegar al punto final. Determinar el% w/w Fe 2 O 3 en la muestra de meteorito.
50. En condiciones básicas,\(\text{MnO}_4^-\) se utiliza como valorante para el análisis de Mn 2 +, formando MnO 2 tanto el analito como el valorante. En el análisis de una muestra mineral para manganeso, se disuelve una muestra de 0.5165-g y el manganeso se reduce a Mn 2 +. La solución se basifica y se titula con 0.03358 M de KMnO 4, requiriendo 34.88 mL para llegar al punto final. Calcular el% w/w de Mn en la muestra mineral.
Algunos de los problemas que siguen requieren una o más constantes de equilibrio o potenciales de estado estándar. Para su comodidad, aquí hay hipervínculos a los apéndices que contienen estas constantes:
Apéndice 10: Productos de solubilidad
Apéndice 11: Constantes de disociación ácida
51. La cantidad de uranio en un mineral se determina mediante una valoración redox indirecta. El análisis se realiza disolviendo el mineral en ácido sulfúrico y reduciendo\(\text{UO}_2^+\) a U 4+ con un reductor Walden. La solución se trata con un exceso de Fe 3 +, formando Fe 2 + y U 6+. El Fe 2 + se titula con una solución estándar de K 2 Cr 2 O 7. En un análisis típico se pasa una muestra de 0.315 g de mineral a través del reductor Walden y se trata con 50.00 mL de 0.0125 M Fe 3 +. La valoración de espalda con 0.00987 M K 2 Cr 2 O 7 requiere 10.52 mL. ¿Cuál es el %w/w U en la muestra?
52. El espesor de la placa de cromo en un auto guardabarros se determina disolviendo una sección de 30.0-cm 2 en ácido y oxidando Cr 3 + a\(\text{Cr}_2\text{O}_7^{2-}\) con peroxidisulfato. Después de eliminar el exceso de peroxidisulfato por ebullición, se agregan 500.0 mg de Fe (NH 4) 2 (SO 4) 2 •6H 2 O, reduciendo el\(\text{Cr}_2\text{O}_7^{2-}\) a Cr 3 +. El exceso de Fe 2 + se vuelve a valorar, requiriendo 18.29 mL de 0.00389 M K 2 Cr 2 O 7 para llegar al punto final. Determinar el grosor promedio de la placa de cromo dado que la densidad de Cr es de 7.20 g/cm 3.
53. La concentración de CO en el aire se determina haciendo pasar un volumen conocido de aire a través de un tubo que contiene I 2 O 5, formando CO 2 e I 2. El I 2 se retira del tubo destilándolo en una solución que contiene un exceso de KI, produciendo\(\text{I}_3^-\). El\(\text{I}_3^-\) se valora con una solución estándar de Na 2 S 2 O 3. En un análisis típico se muestrea una muestra de aire de 4.79-L como se describe aquí, requiriendo 7.17 mL de 0.00329 M Na 2 S 2 O 3 para llegar al punto final. Si el aire tiene una densidad de\(1.23 \times 10^{-3}\) g/mL, determine las partes por millón de CO en el aire.
54. El nivel de oxígeno disuelto en una muestra de agua se determina mediante el método Winkler. En un análisis típico se basifica una muestra de 100.0-mL y se trata con una solución de MnSO 4, dando como resultado la formación de MnO 2. Se agrega un exceso de KI y la solución se acidifica, dando como resultado la formación de Mn 2 + e I 2. El I 2 liberado se titula con una solución de 0.00870 M Na 2 S 2 O 3, requiriendo 8.90 mL para alcanzar el punto final del indicador de almidón. Calcular la concentración de oxígeno disuelto como partes por millón O 2.
55. Calcular o bosquejar la curva de titulación para la titulación de 50.0 mL de 0.0250 M KI con 0.0500 M AgnO 3. Prepare curvas de titulación separadas usando PaG y pI en el eje y.
56. Calcular o bosquejar la curva de titulación para la valoración de una mezcla de 25.0 mL de 0.0500 M KI y 0.0500 M KSCN usando 0.0500 M AgnO 3 como valorante.
57. El análisis para Cl — usando el método Volhard requiere una valoración posterior. Se agrega una cantidad conocida de AgnO 3, precipitando AgCl. El Ag + sin reaccionar se determina por retrotitulación con KSCN. Sin embargo, existe una complicación porque AgCl es más soluble que AgSCn.
a) ¿Por qué las solubilidades relativas de AgCl y AgSCn conducen a un error de titulación?
b) ¿El error de valoración resultante es un error determinado positivo o negativo?
c) ¿Cómo podría modificar el procedimiento para eliminar esta fuente de error determinado?
d) ¿Esta fuente de error determinado es motivo de preocupación cuando se utiliza el método Volhard para determinar Br —?
58. Voncina y sus compañeros de trabajo sugieren que una titulación de precipitación puede ser monitoreada midiendo el pH en función del volumen de valorante si el valorante es una base débil [Vonckina, D. B.; Dobcnik, D.; Gomis, S. Anal. Chim. Acta 1992, 263, 147—153]. Por ejemplo, al valorar Pb 2 + con K 2 CrO 4 la solución que contiene el analito inicialmente se acidifica a un pH de 3.50 usando HNO 3. Antes del punto de equivalencia la concentración de\(\text{CrO}_4^{2-}\) es controlada por el producto de solubilidad de PbCRo 4. Después del punto de equivalencia la concentración de\(\text{CrO}_4^{2-}\) está determinada por la cantidad de exceso de titulante. Considerando las reacciones que controlan la concentración de\(\text{CrO}_4^{2-}\), esbozar la curva de titulación esperada de pH versus volumen de titulante.
59. Una muestra de 0.5131 g que contiene KBr se disuelve en 50 mL de agua destilada. La titulación con 0,04614 M AgnO 3 requiere 25.13 mL para alcanzar el punto final de Mohr. Una valoración en blanco requiere 0.65 mL para alcanzar el mismo punto final. Reporte el %w/w de KBr en la muestra.
60. Se analiza una muestra de 0.1093-g de Na 2 CO 3 impuro por el método de Volhard. Después de agregar 50.00 mL de 0.06911 M AgnO 3, la muestra se vuelve a valorar con 0.05781 M KSCN, requiriendo 27.36 mL para llegar al punto final. Reportar la pureza de la muestra de Na 2 CO 3.
61. Una muestra de 0.1036-g que contiene solo BacL 2 y NaCl se disuelve en 50 mL de agua destilada. La titulación con 0.07916 M AgnO 3 requiere 19.46 mL para alcanzar el punto final de Fajans. Reporte el% w/w BaCl 2 en la muestra.
Algunos de los problemas que siguen requieren una o más constantes de equilibrio o potenciales de estado estándar. Para su comodidad, aquí hay hipervínculos a los apéndices que contienen estas constantes:
Apéndice 10: Productos de solubilidad
Apéndice 11: Constantes de disociación ácida