9.4: Titulaciones redox
- Page ID
- 75417
Las titulaciones analíticas mediante reacciones de oxidación-reducción se introdujeron poco después del desarrollo de la titulación ácido-base. La valoración redox más temprana aprovechó el poder oxidante del cloro. En 1787, Claude Berthollet introdujo un método para el análisis cuantitativo del agua clorada (una mezcla de Cl 2, HCl y HOCl) basado en su capacidad para oxidar el índigo, un tinte que es incoloro en su estado oxidado. En 1814, Joseph Gay-Lussac desarrolló un método similar para determinar el cloro en polvo blanqueador. En ambos métodos el punto final es un cambio de color. Antes del punto de equivalencia la solución es incolora debido a la oxidación del índigo. Después del punto de equivalencia, sin embargo, el índigo sin reaccionar imparte un color permanente a la solución.
El número de métodos de valoración redox aumentó a mediados del siglo XIX con la introducción de\(\text{MnO}_4^-\)\(\text{Cr}_2\text{O}_7^{2-}\), e I 2 como titulantes oxidantes, y de Fe 2 + y\(\text{S}_2\text{O}_3^{2-}\) como titulantes reductores. Incluso con la disponibilidad de estos nuevos titulantes, la titulación redox fue lenta de desarrollarse debido a la falta de indicadores adecuados. Un valorante puede servir como indicador propio si su forma oxidada y sus formas reducidas difieren significativamente en color. Por ejemplo, el\(\text{MnO}_4^-\) ion intensamente púrpura sirve como indicador propio ya que su forma reducida, Mn 2 +, es casi incolora. Otros titulantes requieren un indicador separado. El primer indicador de este tipo, la difenilamina, se introdujo en la década de 1920. Otros indicadores redox pronto siguieron, incrementando la aplicabilidad de la titrimetría redox.
Curvas de valoración redox
Para evaluar una valoración redox necesitamos conocer la forma de su curva de valoración. En una titulación ácido-base o una titulación de complejación, la curva de titulación muestra cómo cambia la concentración de H 3 O + (como pH) o M n + (como pM) a medida que se agrega el valorante. Para una valoración redox es conveniente monitorear el potencial de la reacción de titulación en lugar de la concentración de una especie.
Puede recordar del Capítulo 6 que la ecuación de Nernst relaciona el potencial de una solución con las concentraciones de reactivos y productos que participan en la reacción redox. Consideremos, por ejemplo, una titulación en la que un valorando en estado reducido, A rojo, reacciona con un valorante en estado oxidado, B ox.
\[A_{red} + B_{ox} \rightleftharpoons B_{red} + A_{ox} \nonumber\]
donde A buey es la forma oxidada del titrand, B rojo es la forma reducida del valorante, y la estequiometría entre los dos es 1:1. El potencial de la reacción, E rxn, es la diferencia entre los potenciales de reducción para cada media reacción.
\[E_{rxn} = E_{B_{ox}/B_{red}} - E_{A_{ox}/A_{red}} \nonumber\]
Después de cada adición de valorante, la reacción entre el valorador y el valorante alcanza un estado de equilibrio. Debido a que el potencial en equilibrio es cero, los potenciales de reducción del valor y del valorante son idénticos.
\[E_{B_{ox}/B_{red}} = E_{A_{ox}/A_{red}} \nonumber\]
Esta es una observación importante ya que nos permite utilizar cualquiera de las medias reacciones para monitorear el progreso de la titulación.
Antes del punto de equivalencia, la mezcla de titulación consiste en cantidades apreciables de las formas oxidadas y reducidas de la titrand. La concentración de valorante sin reaccionar, sin embargo, es muy pequeña. El potencial, por lo tanto, es más fácil de calcular si usamos la ecuación de Nernst para la media reacción del título
\[E_{rxn} = E_{A_{ox}/A_{red}}^{\circ} - \frac{RT}{nF}\ln{\frac{[A_{red}]}{[A_{ox}]}} \nonumber\]
Después del punto de equivalencia es más fácil calcular el potencial usando la ecuación de Nernst para la media reacción del valorante.
\[E_{rxn} = E_{B_{ox}/B_{red}}^{\circ} - \frac{RT}{nF}\ln{\frac{[B_{red}]}{[B_{ox}]}} \nonumber\]
Aunque la ecuación de Nernst está escrita en términos del potencial de estado estándar de la media reacción, a menudo se usa en su lugar un potencial formal dependiente de la matriz. Consulte el Apéndice 13 para conocer los potenciales de estado estándar y los potenciales formales para medias reacciones seleccionadas.
Cálculo de la Curva de Titulación
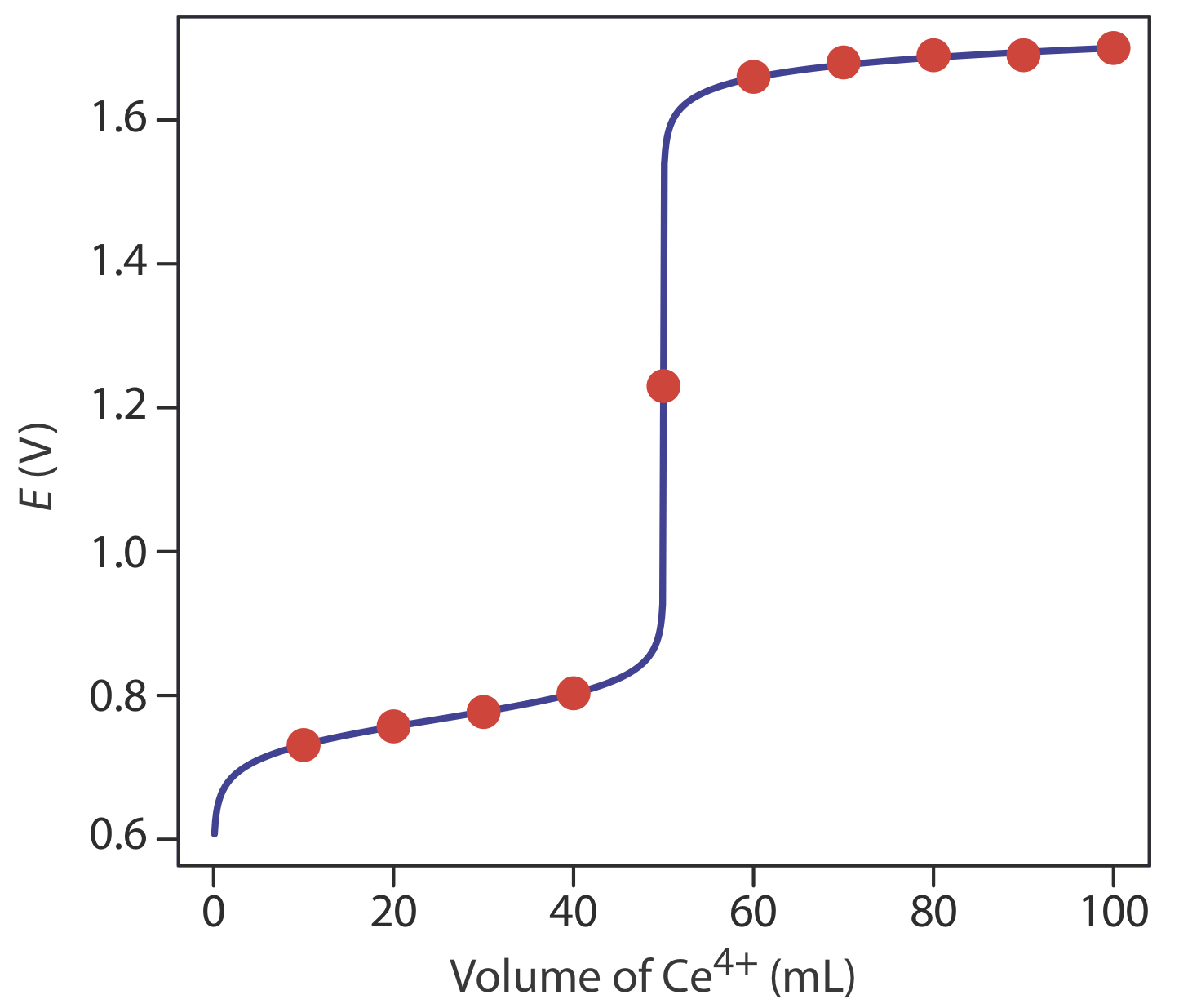
Calculemos la curva de titulación para la titulación de 50.0 mL de 0.100 M Fe 2 + con 0.100 M Ce 4 + en una matriz de 1 M HClO 4. La reacción en este caso es
Debido a que la constante de equilibrio para la reacción\ ref {9.1} es muy grande —es aproximadamente\(6 \times 10^{15}\) — podemos suponer que el analito y el valorante reaccionan completamente.
En 1 M HClO 4, el potencial formal para la reducción de Fe 3 + a Fe 2 + es +0.767 V, y el potencial formal para la reducción de Ce 4 + a Ce 3 + es +1.70 V.
La primera tarea es calcular el volumen de Ce necesario para alcanzar el punto de equivalencia de la titulación. Por la estequiometría de la reacción sabemos que
\[\text{mol Fe}^{2+} = M_\text{Fe}V_\text{Fe} = M_\text{Ce}V_\text{Ce} = \text{mol Ce}^{4+} \nonumber\]
Resolviendo para el volumen de Ce 4 + da el volumen del punto de equivalencia como
\[V_{eq} = V_\text{Ce} = \frac{M_\text{Fe}V_\text{Fe}}{M_\text{Ce}} = \frac{(0.100 \text{ M})(50.0 \text{ mL})}{(0.100 \text{ M})} = 50.0 \text{ mL} \nonumber\]
Antes del punto de equivalencia, la concentración de Fe 2 + sin reaccionar y la concentración de Fe 3 + son fáciles de calcular. Por esta razón encontramos el potencial usando la ecuación de Nernst para la media reacción de Fe 3 + /Fe 2 +.
\[E = +0.767 \text{ V} - 0.05916 \log{\frac{[\text{Fe}^{2+}]}{[\text{Fe}^{3+}]}} \label{9.2}\]
Por ejemplo, las concentraciones de Fe 2 + y Fe 3 + después de agregar 10.0 mL de valorante son
\[[\text{Fe}^{2+}] = \frac{(\text{mol Fe}^{2+})_\text{initial} - (\text{mol Ce}^{4+})_\text{added}}{\text{total volume}} = \frac{M_\text{Fe}V_\text{Fe} - M_\text{Ce}V_\text{Ce}}{V_\text{Fe} + V_\text{Ce}} \nonumber\]
\[[\text{Fe}^{2+}] = \frac{(0.100 \text{ M})(50.0 \text{ mL}) - (0.100 \text{ M})(10.0 \text{ mL})}{50.0 \text{ mL} + 10.0 \text{ mL}} = 6.67 \times 10^{-2} \text{ M} \nonumber\]
\[[\text{Fe}^{3+}] = \frac{(\text{mol Ce}^{4+})_\text{added}}{\text{total volume}} = \frac{M_\text{Ce}V_\text{Ce}}{V_\text{Fe} + V_\text{Ce}} \nonumber\]
\[[\text{Fe}^{3+}] = \frac{(0.100 \text{ M})(10.0 \text{ mL})}{50.0 \text{ mL} + 10.0 \text{ mL}} = 1.67 \times 10^{-2} \text{ M} \nonumber\]
Sustituir estas concentraciones en la Ecuación\ ref {9.2} da el potencial como
\[E = +0.767 \text{ V} - 0.05916 \log{\frac{6.67 \times 10^{-2}}{1.67 \times 10^{-2}}} = +0.731 \text{ V} \nonumber\]
Después del punto de equivalencia, la concentración de Ce 3 + y la concentración de exceso de Ce 4 + son fáciles de calcular. Por esta razón encontramos el potencial usando la ecuación de Nernst para la media reacción de Ce 4 + /Ce 3+ de manera similar a la utilizada anteriormente para calcular potenciales antes del punto de equivalencia.
\[E = +1.70 \text{ V} - 0.05916 \log{\frac{[\text{Ce}^{3+}]}{[\text{Ce}^{4+}]}} \label{9.3}\]
Por ejemplo, después de agregar 60.0 mL de valorante, las concentraciones de Ce 3 + y Ce 4 + son
\[[\text{Ce}^{3+}] = \frac{(\text{mol Fe}^{2+})_\text{initial}}{\text{total volume}} = \frac{M_\text{Fe}V_\text{Fe}}{V_\text{Fe}+V_\text{Ce}} \nonumber\]
\[[\text{Ce}^{3+}] = \frac{(0.100 \text{ M})(50.0 \text{ mL})}{50.0 \text{ mL} + 60.0 \text{ mL}} = 4.55 \times 10^{-2} \text{ M} \nonumber\]
\[[\text{Ce}^{4+}] = \frac{(\text{mol Ce}^{4+})_\text{added}-(\text{mol Fe}^{2+})_\text{initial}}{\text{total volume}} = \frac{M_\text{Ce}V_\text{Ce}-M_\text{Fe}V_\text{Fe}}{V_\text{Fe}+V_\text{Ce}} \nonumber\]
\[[\text{Ce}^{4+}] = \frac{(0.100 \text{ M})(60.0 \text{ mL})-(0.100 \text{ M})(50.0 \text{ mL})}{50.0 \text{ mL} + 60.0 \text{ mL}} = 9.09 \times 10^{-3} \text{ M} \nonumber\]
Sustituir estas concentraciones en la Ecuación\ ref {9.3} da un potencial de
\[E = +1.70 \text{ V} - 0.05916 \log{\frac{4.55 \times 10^{-2} \text{ M}}{9.09 \times 10^{-3} \text{ M}}} = +1.66 \text{ V} \nonumber\]
En el punto de equivalencia de la titulación, el potencial, E eq, en la Ecuación\ ref {9.2} y la Ecuación\ ref {9.3} son idénticos. Sumando las ecuaciones juntas para dar
\[2E_{eq} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} - 0.05916 \log{\frac{[\text{Fe}^{2+}][\text{Ce}^{3+}]}{[\text{Fe}^{3+}][\text{Ce}^{4+}]}} \nonumber\]
Porque [Fe 2 +] = [Ce 4 +] y [Ce 3 +] = [Fe 3+] en el punto de equivalencia, el término logarítmico tiene un valor de cero y el potencial del punto de equivalencia es
\[E_{eq} = \frac{E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ}}{2} = \frac{0.767 \text{ V} + 1.70 \text{ V}}{2} = +1.23 \text{ V} \nonumber\]
Los resultados adicionales para esta curva de titulación se muestran en la Tabla 9.4.1 y la Figura 9.4.1 .
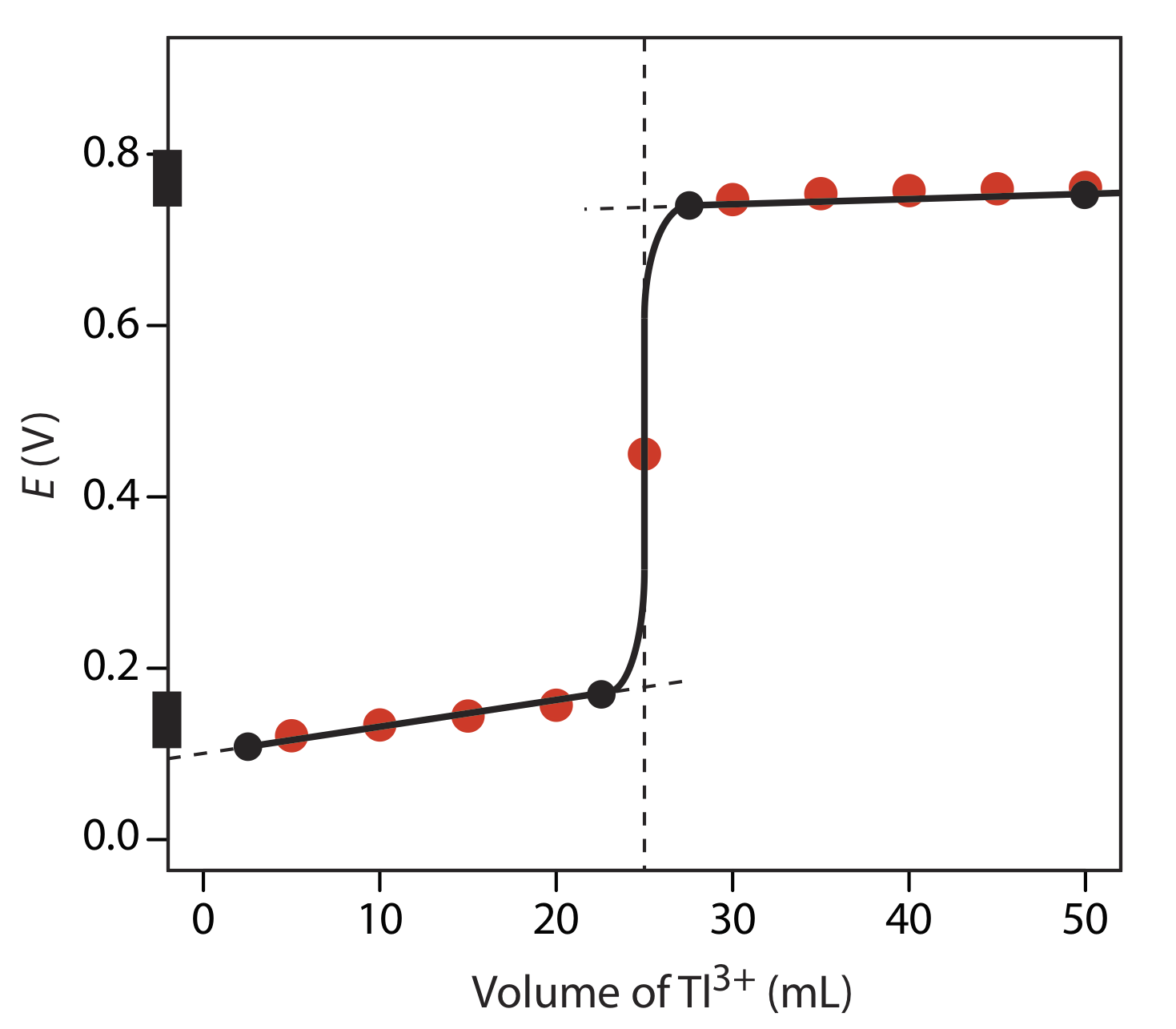
Calcular la curva de titulación para la titulación de 50.0 mL de 0.0500 M Sn 2 + con 0.100 M Tl 3 +. Tanto el titrand como el valorante son 1.0 M en HCl. La reacción de titulación es
\[\text{Sn}^{2+}(aq) + \text{Tl}^{3+} \rightleftharpoons \text{Tl}^+(aq) + \text{Sn}^{4+}(aq) \nonumber\]
- Contestar
-
El volumen de Tl 3 + necesario para alcanzar el punto de equivalencia es
\[V_{eq} = V_\text{Tl} = \frac{M_\text{Sn}V_\text{Sn}}{M_\text{Tl}} = \frac{(0.050 \text{ M})(50.0 \text{ mL})}{(0.100 \text{ M})} = 25.0 \text{ mL} \nonumber\]
Antes del punto de equivalencia, la concentración de Sn 2 + sin reaccionar y la concentración de Sn 4 + son fáciles de calcular. Por esta razón encontramos el potencial usando la ecuación de Nernst para la semirreacción de Sn 4 + /Sn 2+. Por ejemplo, las concentraciones de Sn 2 + y Sn 4 + después de agregar 10.0 mL de valorante son
\[[\text{Sn}^{2+}] = \frac{(0.050 \text{ M})(50.0 \text{ mL}) - (0.100 \text{ M})(10.0 \text{ mL})}{50.0 \text{ mL} + 10.0 \text{ mL}} = 0.0250 \text{ M} \nonumber\]
\[[\text{Sn}^{4+}] = \frac{(0.100 \text{ M})(10.0 \text{ mL})}{50.0 \text{ mL} + 10.0 \text{ mL}} = 0.0167 \text{ M} \nonumber\]
y el potencial es
\[E = +0.139 \text{ V} - \frac{0.05916}{2} \log{\frac{0.0250 \text{ M}}{0.0167 \text{ M}}} = +0.134 \text{ V} \nonumber\]
Después del punto de equivalencia, la concentración de Tl + y la concentración de exceso de Tl 3 + son fáciles de calcular. Por esta razón encontramos el potencial usando la ecuación de Nernst para la media reacción Tl 3 + /Tl +. Por ejemplo, después de agregar 40.0 mL de valorante, las concentraciones de Tl+ y Tl 3 + son
\[[\text{Tl}^{+}] = \frac{(0.050 \text{ M})(50.0 \text{ mL})}{50.0 \text{ mL} + 40.0 \text{ mL}} = 0.0278 \text{ M} \nonumber\]
\[[\text{Tl}^{3+}] = \frac{(0.100 \text{ M})(40.0 \text{ mL}) - (0.050 \text{ M})(50.0 \text{ mL})}{50.0 \text{ mL} + 40.0 \text{ mL}} = 0.0167 \text{ M} \nonumber\]
y el potencial es
\[E = +0.77 \text{ V} - \frac{0.05916}{2} \log{\frac{0.0278 \text{ M}}{0.0167 \text{ M}}} = +0.76 \text{ V} \nonumber\]
En el punto de equivalencia de la titulación, el potencial, E eq, potencial es
\[E_{eq} = \frac{0.139 \text{ V} + 0.77 \text{ V}}{2} = +0.45 \text{ V} \nonumber\]
Aquí se muestran algunos resultados adicionales.
volumen de Tl 3 + (mL) E (V) volumen de Tl 3 + (mL) E (V) 5.00 0.121 30.0 0.75 10.0 0.134 35.0 0.75 15.0 0.144 40.0 0.76 20.0 0.157 45.0 0.76 25.0 0.45
Croquizar una curva de valoración redox
Para evaluar la relación entre el punto de equivalencia de una titulación y su punto final necesitamos construir solo una aproximación razonable de la curva de titulación exacta. En esta sección demostramos un método sencillo para esbozar una curva de valoración redox. Nuestro objetivo es esbozar la curva de valoración rápidamente, utilizando el menor número posible de cálculos. Usemos la titulación de 50.0 mL de 0.100 M Fe 2 + con 0.100 M Ce 4 + en una matriz de 1 M HClO 4.
Este es el mismo ejemplo que utilizamos en el desarrollo de los cálculos para una curva de valoración redox. Puedes revisar los resultados de ese cálculo en Tabla 9.4.1 y Figura 9.4.1 .
Comenzamos calculando el volumen del punto de equivalencia de la titulación, que, como determinamos anteriormente, es de 50.0 mL. A continuación, dibujamos nuestros ejes, colocando el potencial, E, en el eje y y el volumen del valorante en el eje x. Para indicar el volumen del punto de equivalencia, dibujamos una línea vertical que cruza el eje x a 50.0 mL de Ce 4 +. La figura 9.4.2 a muestra el resultado del primer paso en nuestro boceto.
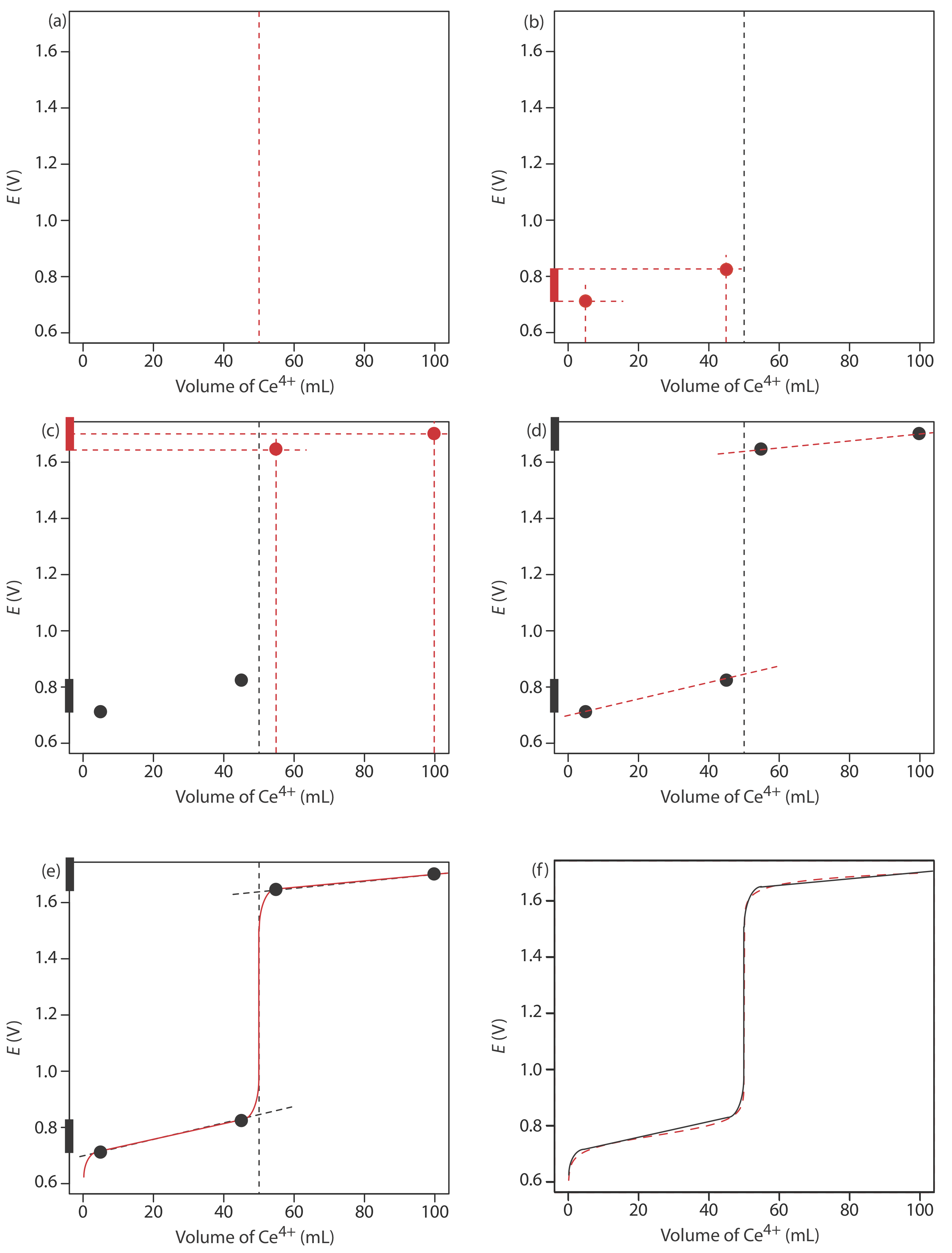
Antes del punto de equivalencia, el potencial es determinado por un búfer redox de Fe 2 + y Fe 3 +. Aunque podemos calcular el potencial usando la ecuación de Nernst, podemos evitar este cálculo si hacemos una suposición simple. Puede recordar del Capítulo 6 que un búfer redox opera sobre un rango de potenciales que se extiende aproximadamente ± (0.05916/ n) unidad a cada lado de\(E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ}\). El potencial en el límite inferior del búfer es
\[E = E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} - 0.05916 \nonumber\]
cuando la concentración de Fe 2 + es\(10 \times\) mayor que la de Fe 3 +. El búfer alcanza su potencial superior de
\[E = E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + 0.05916 \nonumber\]
cuando la concentración de Fe 2 + es\(10 \times\) menor que la de Fe 3 +. El tampón redox abarca un rango de volúmenes desde aproximadamente el 10% del volumen del punto de equivalencia hasta aproximadamente el 90% del volumen del punto de equivalencia. La figura 9.4.2 b muestra el segundo paso de nuestro boceto. Primero, superponemos un diagrama de escalera para Fe en el eje y, utilizando su\(E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ}\) valor de 0.767 V e incluyendo el rango de potenciales del búfer. A continuación, sumamos puntos para el potencial al 10% de V eq (un potencial de 0.708 V a 5.0 mL) y para el potencial al 90% de V eq (un potencial de 0.826 V a 45.0 mL).
Se utilizó un enfoque similar al esbozar la curva de valoración ácido-base para la titulación de ácido acético con NaOH; ver Capítulo 9.2 para más detalles.
El tercer paso para esbozar nuestra curva de valoración es sumar dos puntos después del punto de equivalencia. Aquí el potencial es controlado por un tampón redox de Ce 3 + y Ce 4 +. El búfer redox se encuentra en su límite inferior de
\[E = E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} - 0.05916 \nonumber\]
cuando el valorante alcanza 110% del volumen del punto de equivalencia y el potencial es\(E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ}\) cuando el volumen de Ce es\(2 \times V_{eq}\).
Se utilizó un enfoque similar al esbozar la curva de titulación de complejación para la titulación de Mg 2 + con EDTA; ver Capítulo 9.3 para más detalles.
La figura 9.4.2 c muestra el tercer paso en nuestro boceto. Primero, superponemos un diagrama de escalera para Ce en el eje y, usando su\(E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ}\) valor de 1.70 V e incluyendo el rango del búfer. A continuación, sumamos puntos que representan el potencial al 110% de V eq (un valor de 1.66 V a 55.0 mL) y al 200% de V eq (un valor de 1.70 V a 100.0 mL).
A continuación, dibujamos una línea recta a través de cada par de puntos, extendiendo la línea a través de la línea vertical que indica el volumen del punto de equivalencia (Figura 9.4.2 d). Finalmente, completamos nuestro boceto dibujando una curva suave que conecta los tres segmentos de línea recta (Figura 9.4.2 e). Una comparación de nuestro boceto con la curva de titulación exacta (Figura 9.4.2 f) muestra que están muy de acuerdo.
Dibuje la curva de titulación para la titulación de 50.0 mL de 0.0500 M Sn 4 + con 0.100 M Tl +. Tanto el titrand como el valorante son 1.0 M en HCl. La reacción de titulación es
\[\text{Sn}^{2+}(aq) + \text{Tl}^{3+}(aq) \rightleftharpoons \text{Tl}^{+}(aq) + \text{Sn}^{4+}(aq) \nonumber\]
Compara tu boceto con tu curva de valoración calculada del Ejercicio 9.4.1 .
- Contestar
-
En la siguiente figura se muestra un boceto de la curva de titulación. Los dos puntos antes del punto de equivalencia
V Tl = 2.5 mL, E = +0.109 V y V Tl = 22.5 mL, E = +0.169 V
se representan usando el tampón redox para Sn 4 + /Sn 2+, que abarca un rango de potencial de +0.139 ± 0.5916/2. Los dos puntos después del punto de equivalencia
V Tl = 27.5 mL, E = +0.74 V y V Tl = 50 mL, E = +0.77 V
se representan usando el tampón redox para Tl 3 + /Tl +, que abarca el rango de potencial de +0.139 ± 0.5916/2. Los puntos negros y la curva son el boceto aproximado de la curva de titulación. Los puntos en rojo son los cálculos del Ejercicio 9.4.1 .
Selección y Evaluación del Punto Final
El punto de equivalencia de una titulación redox ocurre cuando reaccionamos con cantidades estequiométricamente equivalentes de titrand y valorante. Como es el caso de las titulaciones ácido-base y las titulaciones de complejación, estimamos el punto de equivalencia de una valoración redox utilizando un punto final experimental. Hay una variedad de métodos disponibles para localizar el punto final de una valoración redox, incluidos indicadores y sensores que responden a un cambio en las condiciones de la solución.
Dónde está el Punto de Equivalencia
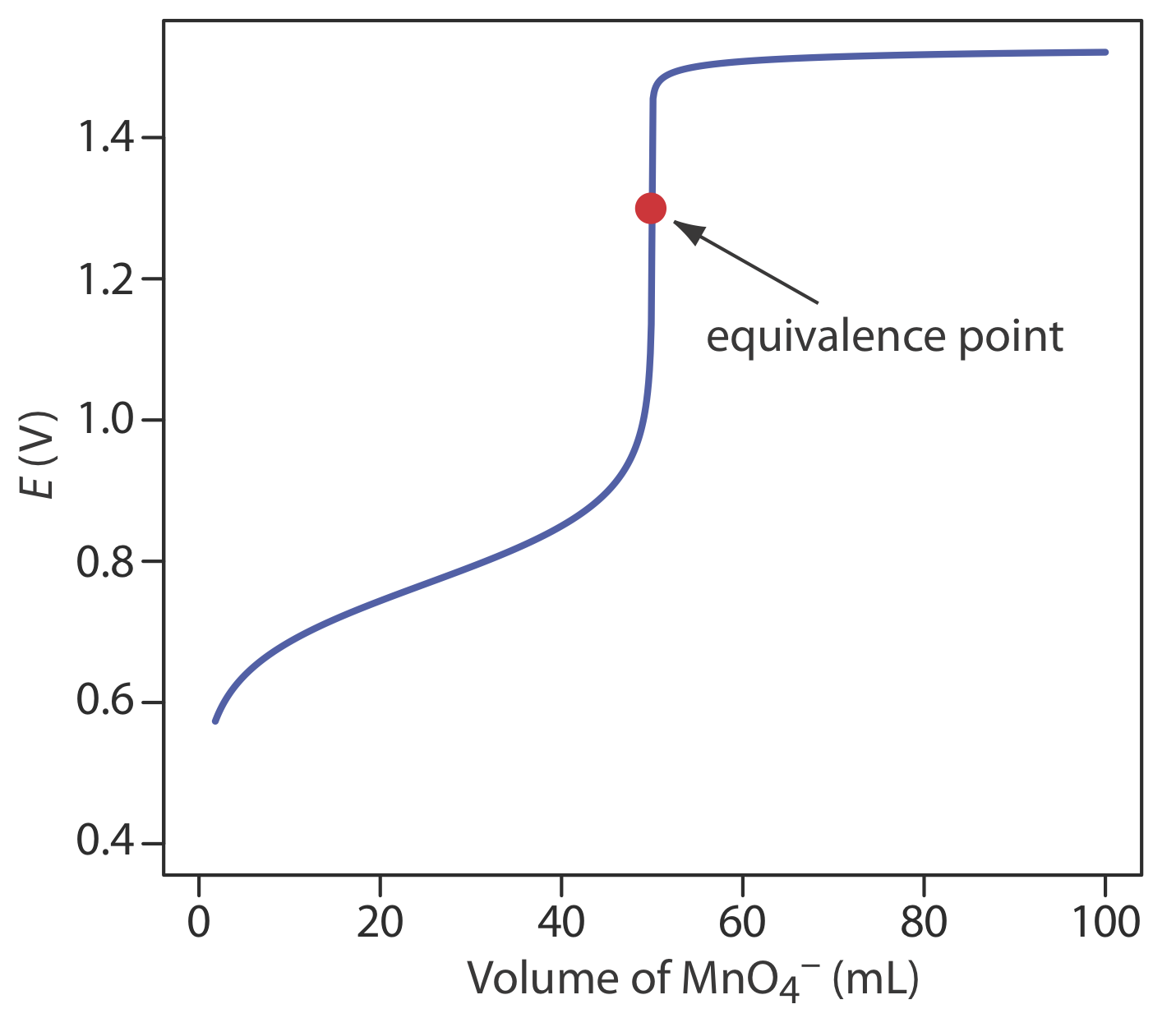
Para una valoración ácido-base o una valoración complejométrica, el punto de equivalencia es casi idéntico al punto de inflexión en la parte pronunciada de la curva de valoración. Si miras hacia atrás en la Figura 9.2.2 y la Figura 9.3.3, verá que el punto de inflexión se encuentra en medio de esta subida pronunciada en la curva de titulación, lo que hace que sea relativamente fácil encontrar el punto de equivalencia cuando dibuje estas curvas de titulación. A esto lo llamamos punto de equivalencia simétrica. Si la estequiometría de una valoración redox es 1:1 —es decir, un mol de valorante reacciona con cada mol de titulación—entonces el punto de equivalencia es simétrico. Si la estequiometría de la reacción de titulación no es 1:1, entonces el punto de equivalencia está más cerca de la parte superior o de la parte inferior de la fuerte subida de la curva de titulación. En este caso tenemos un punto de equivalencia asimétrica.
Derivar una ecuación general para el potencial del punto de equivalencia al valorar Fe 2 + con\(\text{MnO}_4^-\).
\[5\text{Fe}^{2+}(aq) + \text{MnO}_4^-(aq) + 8\text{H}^+(aq) \rightarrow 5\text{Fe}^{3+}(aq) + \text{Mn}^{2+}(aq) + 4\text{H}_2\text{O}(l) \nonumber\]
Solución
Las medias reacciones para la oxidación de Fe 2 + y la reducción de\(\text{MnO}_4^-\) son
\[\text{Fe}^{2+}(aq) \rightarrow \text{Fe}^{3+}(aq) + e^- \nonumber\]
\[\text{MnO}_4^-(aq) + 8\text{H}^+(aq) + 5 e^- \rightarrow \text{Mn}^{2+}(aq) + 4\text{H}_2\text{O}(l) \nonumber\]
para lo cual las ecuaciones de Nernst son
\[E = E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} - 0.5916 \log{\frac{[\text{Fe}^{2+}]}{[\text{Fe}^{3+}]}} \nonumber\]
\[E = E_{\text{MnO}_4^{-}/\text{Mn}^{2+}}^{\circ} - \frac{0.5916}{5} \log{\frac{[\text{Mn}^{2+}]}{[\text{MnO}_4^{-}][\text{H}^+]^8}} \nonumber\]
Antes de sumar estas dos ecuaciones debemos multiplicar la segunda ecuación por 5 para que podamos combinar los términos logarítmicos; así
\[6E_{eq} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + 5E_{\text{MnO}_4^{-}/\text{Mn}^{2+}}^{\circ} - 0.05916 \log{\frac{[\text{Fe}^{2+}][\text{Mn}^{2+}]}{[\text{Fe}^{3+}][\text{MnO}_4^{-}][\text{H}^+]^8}} \nonumber\]
En el punto de equivalencia sabemos que
\[[\text{Fe}^{2+}] = 5 \times [\text{MnO}_4^-] \text{ and } [\text{Fe}^{3+}] = 5 \times [\text{Mn}^{2+}] \nonumber\]
Sustituir estas igualdades en la ecuación anterior y reordenarlo nos da una ecuación general para el potencial en el punto de equivalencia.
\[6E_{eq} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + 5E_{\text{MnO}_4^{-}/\text{Mn}^{2+}}^{\circ} - 0.05916 \log{\frac{5[\text{MnO}_4^{-}][\text{Mn}^{2+}]}{5[\text{Mn}^{2+}][\text{MnO}_4^{-}][\text{H}^+]^8}} \nonumber\]
\[E_{eq} = \frac{E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + 5E_{\text{MnO}_4^{-}/\text{Mn}^{2+}}^{\circ}}{6} - \frac{0.05916}{6} \log{\frac{1}{[\text{H}^+]^8}} \nonumber\]
\[E_{eq} = \frac{E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + 5E_{\text{MnO}_4^{-}/\text{Mn}^{2+}}^{\circ}}{6} + \frac{0.05916 \times 8}{6} \log{[\text{H}^+]} \nonumber\]
\[E_{eq} = \frac{E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} + 5E_{\text{MnO}_4^{-}/\text{Mn}^{2+}}^{\circ}}{6} - 0.07888 \text{pH} \nonumber\]
Nuestra ecuación para el punto de equivalencia tiene dos términos. El primer término es un promedio ponderado de los potenciales de estado estándar del valorante y del valorante, en el que los factores de ponderación son el número de electrones en sus respectivas medias reacciones. El segundo término muestra que E eq para esta titulación es dependiente del pH. A un pH de 1 (en H 2 SO 4), por ejemplo, el punto de equivalencia tiene un potencial de
\[E_{eq} = \frac{0.768 + 5 \times 1.51}{6} - 0.07888 \times 1 = 1.31 \text{ V} \nonumber\]
La figura 9.4.3 muestra una curva de titulación típica para la titulación de Fe 2 + con\(\text{MnO}_4^-\). Tenga en cuenta que el punto de equivalencia de la titulación es asimétrico.
Derivar una ecuación general para el potencial del punto de equivalencia para la titulación de U 4+ con Ce 4 +. La reacción desequilibrada es
\[\text{Ce}^{4+}(aq) + \text{U}^{4+}(aq) \rightarrow \text{UO}_2^{2+}(aq) + \text{Ce}^{3+}(aq) \nonumber\]
¿Cuál es el potencial del punto de equivalencia si el pH es 1?
- Contestar
-
Las dos medias reacciones son
\[\text{Ce}^{4+}(aq) + e^- \rightarrow \text{Ce}^{3+}(aq) \nonumber\]
\[\text{U}^{4+}(aq) +2\text{H}_2\text{O}(l) \rightarrow \text{UO}_2^{2+}(aq)) + 4\text{H}^+(aq) +2e^- \nonumber\]
para lo cual las ecuaciones de Nernst son
\[E = E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} - 0.05916 \log{\frac{[\text{Ce}^{3+}]}{[\text{Ce}^{4+}]}} \nonumber\]
\[E = E_{\text{UO}_2^{2+}/\text{U}^{4+}}^{\circ} - \frac{0.05916}{2} \log{\frac{[\text{U}^{4+}]}{[\text{UO}_2^{2+}][\text{H}^+]^4}} \nonumber\]
Antes de sumar estas dos ecuaciones debemos multiplicar la segunda ecuación por 2 para que podamos combinar los términos logarítmicos; así
\[3E = E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} + 2E_{\text{UO}_2^{2+}/\text{U}^{4+}}^{\circ} - 0.05916 \log{\frac{[\text{Ce}^{3+}][\text{U}^{4+}]}{[\text{Ce}^{4+}][\text{UO}_2^{2+}][\text{H}^+]^4}} \nonumber\]
En el punto de equivalencia sabemos que
\[[\text{Ce}^{3+}] = 2 \times [\text{UO}_2^{2+}] \text{ and } [\text{Ce}^{4+}] = 2 \times [\text{U}^{4+}] \nonumber\]
Sustituir estas igualdades en la ecuación anterior y reordenarlo nos da una ecuación general para el potencial en el punto de equivalencia.
\[3E = E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} + 2E_{\text{UO}_2^{2+}/\text{U}^{4+}}^{\circ} - 0.05916 \log{\frac{2[\text{UO}_2^{2+}][\text{U}^{4+}]}{2[\text{U}^{4+}][\text{UO}_2^{2+}][\text{H}^+]^4}} \nonumber\]
\[E = \frac{E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} + 2E_{\text{UO}_2^{2+}/\text{U}^{4+}}^{\circ}}{3} - \frac{0.05916}{3} \log{\frac{1}{[\text{H}^+]^4}} \nonumber\]
\[E = \frac{E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} + 2E_{\text{UO}_2^{2+}/\text{U}^{4+}}^{\circ}}{3} + \frac{0.05916 \times 4}{3} \log{[\text{H}^+]^4} \nonumber\]
\[E = \frac{E_{\text{Ce}^{4+}/\text{Ce}^{3+}}^{\circ} + 2E_{\text{UO}_2^{2+}/\text{U}^{4+}}^{\circ}}{3} - 0.07888\text{pH} \nonumber\]
A un pH de 1 el punto de equivalencia tiene un potencial de
\[E = \frac{1.72 + 2 \times 0.327}{3} - 0.07888 \times 1 = +0.712 \text{ V} \nonumber\]
Encontrar el punto final con un indicador
Se utilizan tres tipos de indicadores para señalar el punto final de una valoración redox. Las formas oxidadas y reducidas de algunos titulantes, como\(\text{MnO}_4^-\), tienen diferentes colores. Una solución de\(\text{MnO}_4^-\) es intensamente púrpura. En una solución ácida, sin embargo, la forma reducida del permanganato, Mn 2 +, es casi incolora. Cuando se usa\(\text{MnO}_4^-\) como valorante, la solución del titrand permanece incolora hasta el punto de equivalencia. La primera gota de exceso\(\text{MnO}_4^-\) produce un tinte permanente de púrpura, señalando el punto final.
Algunos indicadores forman un compuesto coloreado con una forma específica oxidada o reducida del valorante o del titrand. El almidón, por ejemplo, forma un complejo de color púrpura oscuro con\(\text{I}_3^-\). Podemos usar este color distinto para señalar la presencia de exceso\(\text{I}_3^-\) como titulante, un cambio de color de incoloro a púrpura, o la finalización de una reacción que consume\(\text{I}_3^-\) como título, un cambio de color de púrpura a incoloro. Otro ejemplo de un indicador específico es el tiocianato, SCN —, que forma el complejo soluble de color rojo de Fe (SCN) 2+ en presencia de Fe 3 +.
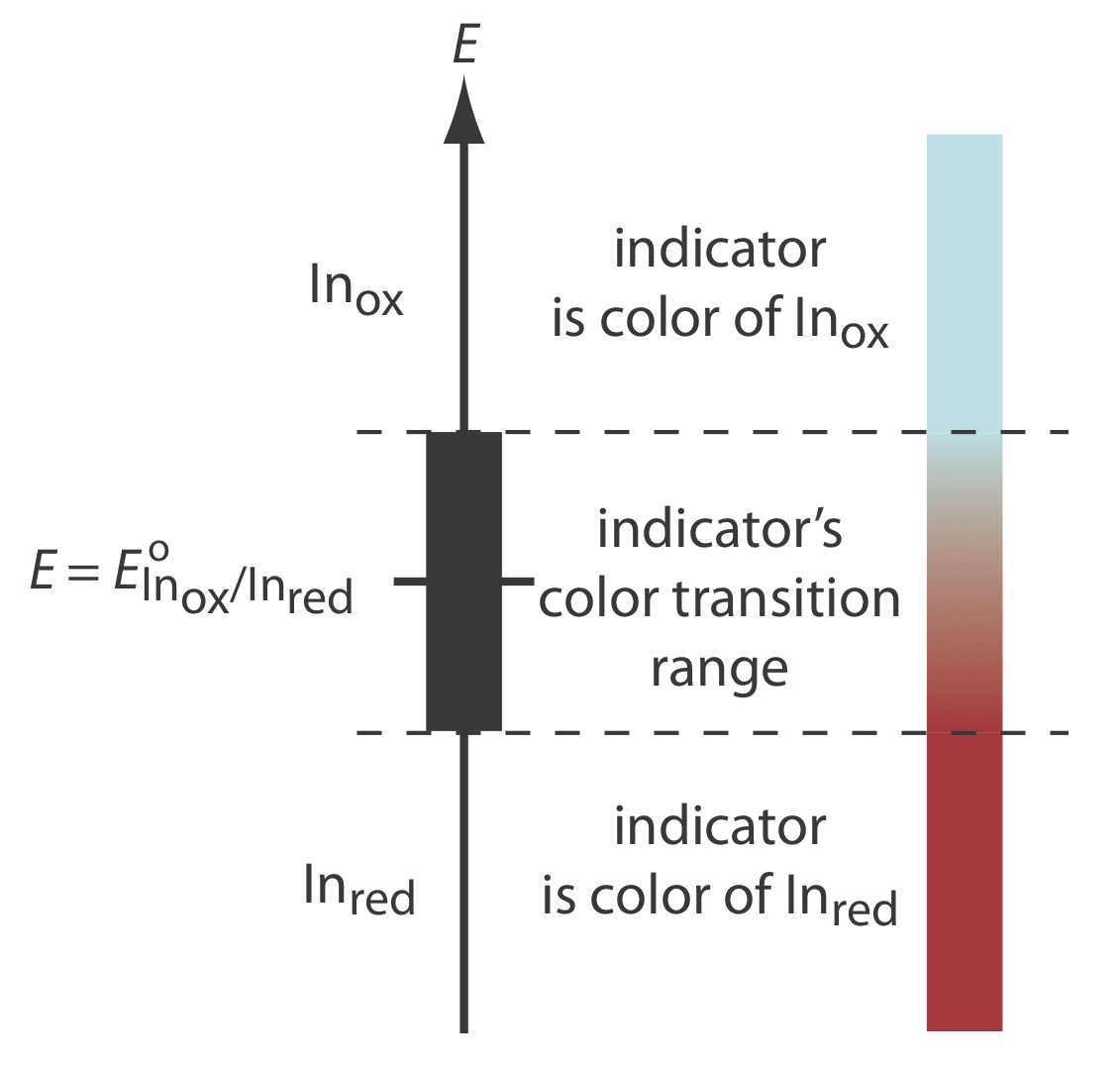
La clase de indicadores más importante son las sustancias que no participan en la titulación redox, pero cuyas formas oxidadas y reducidas difieren en color. Cuando agregamos un indicador redox a la titrand, el indicador imparte un color que depende del potencial de la solución. A medida que el potencial de la solución cambia con la adición de valorante, el indicador eventualmente cambia el estado de oxidación y cambia de color, señalando el punto final.
Para comprender la relación entre el potencial y el color de un indicador, considere su media reacción de reducción
\[\text{In}_\text{ox} + ne^- \rightleftharpoons \text{In}_\text{red} \nonumber\]
donde En buey y En rojo son, respectivamente, las formas oxidadas y reducidas del indicador.
Por simplicidad, En buey y En rojo se muestran sin cargas específicas. Debido a que hay un cambio en el estado de oxidación, En buey y En rojo no pueden ser ambos neutros.
La ecuación de Nernst para esta media reacción es
\[E = E_{\text{In}_\text{ox}/\text{In}_\text{red}}^{\circ} - \frac{0.05916}{n} \log{\frac{[\text{In}_\text{red}]}{[\text{In}_\text{ox}]}} \nonumber\]
Como se muestra en la Figura 9.4.4 , si asumimos que el color del indicador cambia del de En buey al de En rojo cuando la relación [En rojo]/[En buey] cambia de 0.1 a 10, entonces el punto final ocurre cuando el potencial de la solución está dentro del rango
\[E = E_{\text{In}_\text{ox}/\text{In}_\text{red}}^{\circ} \pm \frac{0.05916}{n} \nonumber\]
Este es el mismo enfoque que tomamos al considerar los indicadores ácido-base y los indicadores de complejación.
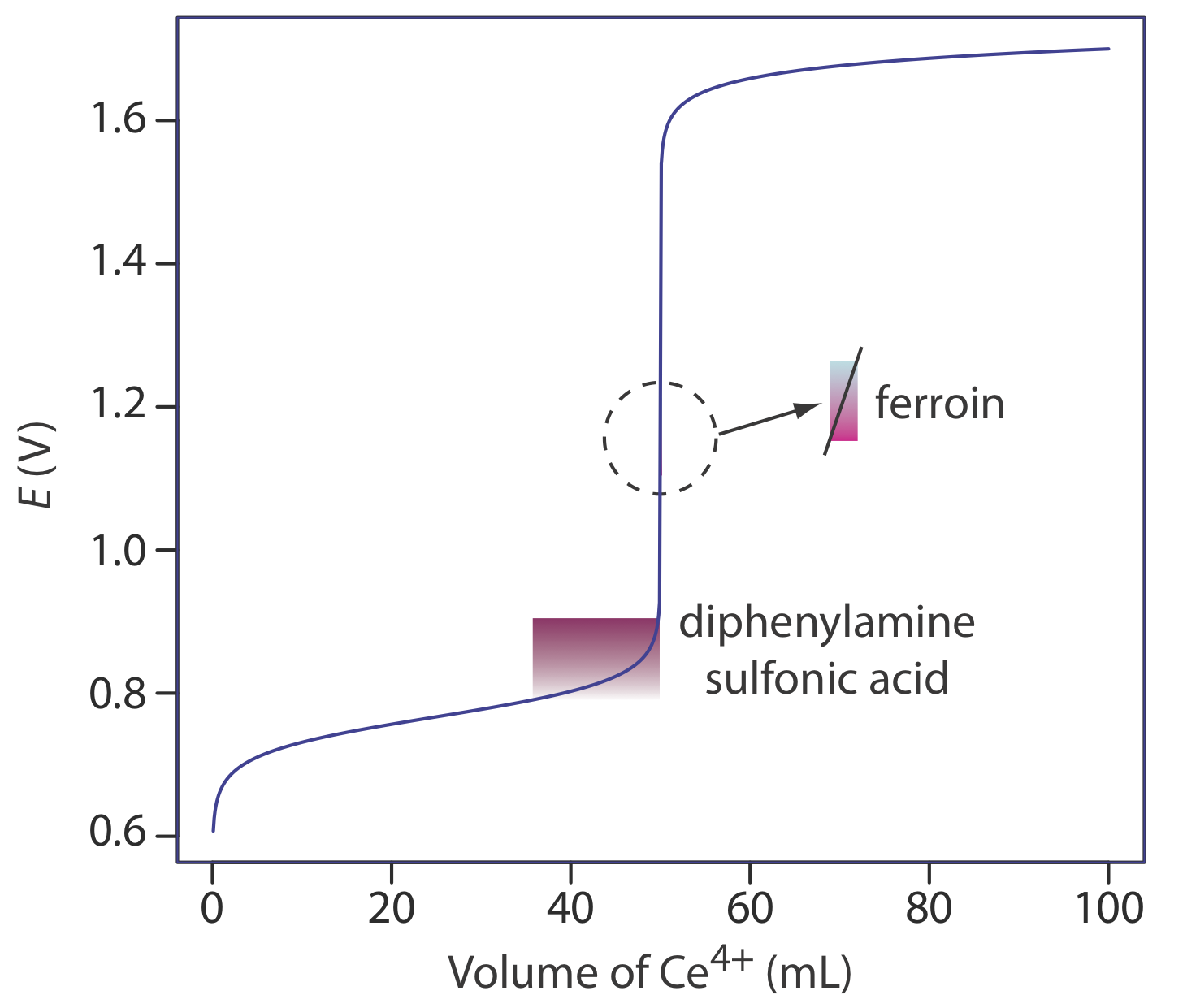
Una lista parcial de indicadores redox se muestra en la Tabla 9.4.2 . En la Figura 9.4.5 se muestran ejemplos de un indicador apropiado e inapropiado para la titulación de Fe 2 + con Ce 4 +.
Otros métodos para encontrar el punto final
Otro método para localizar el punto final de una valoración redox es una valoración potenciométrica en la que monitoreamos el cambio en el potencial mientras agregamos el valorante a la banda de valoración. El punto final se encuentra examinando visualmente la curva de titulación. El diseño experimental más simple para una valoración potenciométrica consiste en un electrodo indicador de Pt cuyo potencial está gobernado por la media reacción redox del valorador o del valorante, y un electrodo de referencia que tiene un potencial fijo. Otros métodos para localizar el punto final de la titulación incluyen valoraciones termométricas y valoraciones espectrofotométricas.
Serás una discusión más a fondo sobre la potenciometría en el Capítulo 11.
Método Representativo 9.4.1: Determinación de Cloro Residual Total
La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método típico de valoración redox. Aunque cada método es único, la siguiente descripción de la determinación del cloro total residual en el agua proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en el Método 4500-Cl B publicado en Standard Methods for the Examination of Water and Wastewater, 20th Ed., American Public Health Association: Washington, D. C., 1998.
Descripción del Método
La cloración de un suministro público de agua produce varias especies que contienen cloro, cuya concentración combinada se denomina cloro residual total. El cloro está presente en una variedad de estados químicos, incluyendo el cloro residual libre, que consiste en Cl 2, HOCl y OCl —, y el cloro residual combinado, que consiste en NH 2 Cl, NHCl 2 y NCl 3. El cloro residual total se determina usando el poder oxidante del cloro para convertir I — a\(\text{I}_3^-\). La cantidad de\(\text{I}_3^-\) formado se determina luego valorando con Na 2 S 2 O 3 usando almidón como indicador. Independientemente de su forma, el residuo de cloro total se reporta como si Cl 2 es la única fuente de cloro, y se reporta como mg Cl/L.
Procedimiento
Seleccionar un volumen de muestra que requiera menos de 20 mL de Na 2 S 2 O 3 para llegar al punto final. Usando ácido acético glacial, acidificar la muestra a un pH entre 3 y 4, y agregar aproximadamente 1 gramo de KI. Titular con Na 2 S 2 O 3 hasta que el color amarillo de\(\text{I}_3^-\) comience a desaparecer. Agregar 1 mL de una solución indicadora de almidón y continuar titulando hasta que desaparezca el color azul del\(\text{I}_3^-\) complejo starch— (Figura 9.4.6 ). Use una titulación en blanco para corregir el volumen de valorante necesario para alcanzar el punto final para las impurezas del reactivo.
Preguntas
1. ¿Es este un ejemplo de un análisis directo o indirecto?
Este es un análisis indirecto porque las especies que contienen cloro no reaccionan con el valorante. En cambio, el cloro residual total oxida I — a\(\text{I}_3^-\), y la cantidad de\(\text{I}_3^-\) se determina valorando con Na 2 S 2 O 3.
2. ¿Por qué el procedimiento se basa en un análisis indirecto en lugar de valorar directamente las especies que contienen cloro usando KI como valorante?
Debido a que el cloro residual total consta de seis especies diferentes, una titulación con I — no tiene un solo punto de equivalencia bien definido. Al convertir el cloro residual en una cantidad equivalente de\(\text{I}_3^-\), la titulación indirecta con Na 2 S 2 O 3 tiene un único punto de equivalencia útil. Incluso si el cloro residual total es de una sola especie, como el HOCl, una titulación directa con KI no es práctica. Debido a que el producto de la titulación\(\text{I}_3^-\),, imparte un color amarillo, el color de la titrand cambiaría con cada adición de valorante, dificultando la búsqueda de un indicador adecuado.
3. Tanto los agentes oxidantes como los reductores pueden interferir con este análisis. Explicar el efecto de cada tipo de interferente sobre el cloro residual total.
Un interferente que es un agente oxidante convierte I — a adicional\(\text{I}_3^-\). Debido a que este extra\(\text{I}_3^-\) requiere un volumen adicional de Na 2 S 2 O 3 para llegar al punto final, sobrestimamos el cloro residual total. Si el interferente es un agente reductor, vuelve a disminuir a I —algunos de los\(\text{I}_3^-\) producidos por la reacción entre el cloro residual total y el yoduro; como resultado, subestimamos el cloro residual total.
Aplicaciones Cuantitativas
Aunque muchas aplicaciones cuantitativas de la titrimetría redox han sido reubicadas por otros métodos analíticos, algunas aplicaciones importantes continúan encontrando relevancia. En esta sección revisamos la aplicación general de la titrimetría redox con énfasis en aplicaciones ambientales, farmacéuticas e industriales. Comenzamos, sin embargo, con una breve discusión sobre la selección y caracterización de los titulantes redox y los métodos para controlar el estado de oxidación de la titrand.
Ajuste del estado de oxidación del campo de valoración
Si se va a utilizar una valoración redox en un análisis cuantitativo, la titulación inicialmente debe estar presente en un solo estado de oxidación. Por ejemplo, el hierro se determina mediante una titulación redox en la que Ce 4 + oxida Fe 2 + a Fe 3 +. Dependiendo de la muestra y el método de preparación de la muestra, el hierro inicialmente puede estar presente tanto en los estados de oxidación +2 como +3. Antes de la titulación, debemos reducir cualquier Fe 3 + a Fe 2 + si queremos determinar la concentración total de hierro en la muestra. Este tipo de pretratamiento se realiza usando un agente reductor auxiliar o agente oxidante.
Un metal que es fácil de oxidar, como Zn, Al y Ag, puede servir como agente reductor auxiliar. El metal, como alambre enrollado o polvo, se agrega a la muestra donde reduce el valor. Debido a que cualquier agente reductor auxiliar sin reaccionar reaccionará con el valorante, se elimina antes de comenzar la titulación retirando el alambre enrollado o filtrando.
Un método alternativo para usar un agente reductor auxiliar es inmovilizarlo en una columna. Para preparar una columna de reducción se empaqueta una lechada acuosa del metal finalmente dividido en un tubo de vidrio equipado con un tapón poroso en la parte inferior. La muestra se coloca en la parte superior de la columna y se mueve a través de la columna bajo la influencia de la gravedad o succión al vacío. La longitud de la columna de reducción y el caudal se seleccionan para asegurar la reducción completa del analito.
Se utilizan dos columnas de reducción comunes. En el reductor Jones la columna se rellena con zinc amalgamado, Zn (Hg), el cual se prepara colocando brevemente gránulos de Zn en una solución de HgCl 2. Oxidación de zinc
\[\text{Zn(Hg)}(s) \rightarrow \text{Zn}^{2+}(aq) + \text{Hg}(l) + 2e^- \nonumber\]
proporciona los electrones para reducir la titrand. En el reductor Walden la columna se rellena con metal Ag granular. La solución que contiene el titrand se acidifica con HCl y se hace pasar a través de la columna donde se produce la oxidación de la plata
\[\text{Ag}(s) + \text{Cl}^- (aq) \rightarrow \text{AgCl}(s) + e^- \nonumber\]
proporciona los electrones necesarios para reducir la titrand. Table 9.4.3 proporciona un resumen de varias aplicaciones de columnas de reducción.
Se utilizan varios reactivos como agentes oxidantes auxiliares, entre ellos peroxidisulfato amónico, (NH 4) 2 S 2 O 8, y peróxido de hidrógeno, H 2 O 2. El peroxidisulfato es un poderoso agente oxidante
\[\text{S}_2\text{O}_8^{2-}(aq) + 2e^- \rightarrow 2\text{SO}_4^{2-}(aq) \nonumber\]
que sea capaz de oxidar Mn 2 + a\(\text{MnO}_4^-\), Cr 3 + a\(\text{Cr}_2\text{O}_7^{2-}\), y Ce 3 + a Ce 4 +. El exceso de peroxidisulfato se destruye hirviendo brevemente la solución. La reducción del peróxido de hidrógeno en una solución ácida
\[\text{H}_2\text{O}_2(aq) + 2\text{H}^+(aq) + 2e^- \rightarrow 2\text{H}_2\text{O}(l) \nonumber\]
proporciona otro método para oxidar un grupo de titulación. El exceso de H 2 O 2 se destruye hirviendo brevemente la solución.
Selección y estandarización de un valorante
Si se va a utilizar cuantitativamente, la concentración del valorante debe permanecer estable durante el análisis. Debido a que un valorante en estado reducido es susceptible a la oxidación del aire, la mayoría de las titulaciones redox utilizan un agente oxidante como valorante. Hay varios titulantes oxidantes comunes, incluyendo\(\text{MnO}_4^-\), Ce 4 +,\(\text{Cr}_2\text{O}_7^{2-}\), y\(\text{I}_3^-\). El titulante que se usa a menudo depende de la facilidad con la que oxida el titrand. Una titrand que es un agente reductor débil necesita un valorante oxidante fuerte si la reacción de titulación va a tener un punto final adecuado.
Los dos titulantes oxidantes más fuertes son\(\text{MnO}_4^-\) y Ce 4 +, para lo cual las medias reacciones de reducción son
\[\text{MnO}_4^-(aq) + 8\text{H}^+(aq) + 5e^- \rightleftharpoons \text{Mn}^{2+}(aq) + 4\text{H}_2\text{O}(l) \nonumber\]
\[\text{Ce}^{4+}(aq) + e^- \rightleftharpoons \text{Ce}^{3+}(aq) \nonumber\]
Una solución de Ce 4 + en 1 M H 2 SO 4 generalmente se prepara a partir del estándar primario de nitrato de amonio de cerio, Ce (NO 3) 4 •2NH 4 NO 3. Cuando se prepara usando un material de grado reactivo, como Ce (OH) 4, la solución se estandariza contra un agente reductor estándar primario como Na 2 C 2 O 4 o Fe 2 + (preparado a partir de alambre de hierro) usando ferroína como indicador. A pesar de su disponibilidad como estándar primario y su facilidad de preparación, el Ce 4 + no se usa con tanta frecuencia como\(\text{MnO}_4^-\) porque es más caro.
Las reacciones de estandarización son
\[\text{Ce}^{4+}(aq) + \text{Fe}^{2+}(aq) \rightarrow \text{Fe}^{3+}(aq) + \text{Ce}^{3+}(aq) \nonumber\]
\[2\text{Ce}^{4+}(aq) + \text{H}_2\text{C}_2\text{O}_4(aq) \rightarrow 2\text{Ce}^{3+}(aq) + 2\text{CO}_2(g) + 2\text{H}^+(aq) \nonumber\]
Una solución de\(\text{MnO}_4^-\) se prepara a partir de KMnO 4, que no está disponible como estándar primario. Una solución acuosa de permanganato es termodinámicamente inestable debido a su capacidad para oxidar el agua.
\[4\text{MnO}_4^-(aq) + 2\text{H}_2\text{O}(l) \rightleftharpoons 4\text{MnO}_2(s) + 3\text{O}_2 (g) + 4\text{OH}^-(aq) \nonumber\]
Esta reacción es catalizada por la presencia de MnO 2, Mn 2 +, calor, luz y la presencia de ácidos y bases. Se prepara una solución moderadamente estable de permanganato hirviéndola durante una hora y filtrándola a través de un filtro de vidrio sinterizado para eliminar cualquier MnO 2 sólido que precipite. La estandarización se logra frente a un agente reductor estándar primario como Na 2 C 2 O 4 o Fe 2 + (preparado a partir de alambre de hierro), con el color rosa del exceso\(\text{MnO}_4^-\) señalando el punto final. Una solución de\(\text{MnO}_4^-\) preparado de esta manera es estable por 1—2 semanas, aunque se debe volver a verificar la estandarización periódicamente.
Las reacciones de estandarización son
\[\text{MnO}_4^-(aq) + 5\text{Fe}^{2+}(aq) + 8\text{H}^+(aq) \rightarrow \text{Mn}^{2+}(aq) + 5\text{Fe}^{3+}(aq) + 4\text{H}_2\text{O}(l) \nonumber\]
\[2\text{MnO}_4^-(aq) + 5\text{H}_2\text{C}_2\text{O}_4(aq) + 6\text{H}^+(aq) \rightarrow 2\text{Mn}^{2+}(aq) + 10\text{CO}_2(g) + 8\text{H}_2\text{O}(l) \nonumber\]
El dicromato de potasio es un agente oxidante relativamente fuerte cuyas principales ventajas son su disponibilidad como estándar primario y su estabilidad a largo plazo cuando está en solución. Sin embargo, no es un agente oxidante tan fuerte como\(\text{MnO}_4^-\) el Ce 4 +, lo que lo hace menos útil cuando el título es un agente reductor débil. Su media reacción de reducción es
\[\text{Cr}_2\text{O}_7^{2-}(aq) + 14\text{H}^+(aq) + 6e^- \rightleftharpoons 2\text{Cr}^{3+}(aq) + 7\text{H}_2\text{O}(l) \nonumber\]
Si bien una solución de\(\text{Cr}_2\text{O}_7^{2-}\) es naranja y una solución de Cr 3 + es verde, ninguno de los dos colores es lo suficientemente intenso como para servir como indicador útil. El ácido difenilaminosulfónico, cuya forma oxidada es rojo-violeta y la forma reducida es incolora, da una señal de punto final muy distinta con\(\text{Cr}_2\text{O}_7^{2-}\).
El yodo es otro importante valorante oxidante. Debido a que es un agente oxidante más débil que\(\text{MnO}_4^-\), Ce 4 +\(\text{Cr}_2\text{O}_7^{2-}\), y, es útil solo cuando la titrand es un agente reductor más fuerte. Esta aparente limitación, sin embargo, hace que I 2 sea un valorante más selectivo para el análisis de un agente reductor fuerte en presencia de un agente reductor más débil. La media reacción de reducción para I 2 es
\[\text{I}_2(aq) + 2e^- \rightleftharpoons 2\text{I}^-(aq) \nonumber\]
Debido a que el yodo no es muy soluble en agua, las soluciones se preparan añadiendo un exceso de I —. La reacción de complejación
\[\text{I}_2(aq) + \text{I}^-(aq) \rightleftharpoons \text{I}_3^-(aq) \nonumber\]
aumenta la solubilidad de I 2 formando el ion triyoduro más soluble,\(\text{I}_3^-\). A pesar de que el yodo está presente como\(\text{I}_3^-\) en lugar de I 2, el número de electrones en la media reacción de reducción no se ve afectado.
\[\text{I}_3^-(aq) + 2e^-(aq) \rightleftharpoons 3\text{I}^-(aq) \nonumber\]
Las soluciones de\(\text{I}_3^-\) normalmente se estandarizan contra Na 2 S 2 O 3 usando almidón como indicador específico para\(\text{I}_3^-\).
La reacción de estandarización es
\[\text{I}_3^-(aq) + 2\text{S}_2\text{O}_3^{2-}(aq) \rightarrow 3\text{I}^-(aq) + 2\text{S}_4\text{O}_6^{2-} (aq) \nonumber\]
Un valorante oxidante tal como\(\text{MnO}_4^-\), Ce 4 +\(\text{Cr}_2\text{O}_7^{2-}\), y\(\text{I}_3^-\), se usa cuando el título está en un estado reducido. Si la titrand está en estado oxidado, primero podemos reducirla con un agente reductor auxiliar y luego completar la titulación usando un valorante oxidante. Alternativamente, podemos valorarlo usando un valorante reductor. El yoduro es un agente reductor relativamente fuerte que podría servir como valorante reductor excepto que sus soluciones son susceptibles a la oxidación al aire de I — a\(\text{I}_3^-\).
\[3\text{I}^-(aq) \rightleftharpoons \text{I}_3^- (aq) + 2e^- \nonumber\]
Una solución recién preparada de KI es transparente, pero después de unos días puede mostrar una tenue coloración amarilla debido a la presencia de\(\text{I}_3^-\).
En cambio, agregar un exceso de KI reduce el valor y libera una cantidad estequiométrica de\(\text{I}_3^-\). La cantidad de\(\text{I}_3^-\) producto se determina luego mediante una retrotitulación usando tiosulfato\(\text{S}_2\text{O}_3^{2-}\),, como valorante reductor.
\[2\text{S}_2\text{O}_3^{2-}(aq) \rightleftharpoons \text{S}_4\text{O}_6^{2-}(aq) + 2e^- \nonumber\]
Las soluciones de\(\text{S}_2\text{O}_3^{2-}\) se preparan usando Na 2 S 2 O 3 •5H 2 O y se estandarizan antes de su uso. La estandarización se logra disolviendo una porción cuidadosamente pesada del estándar primario KIO 3 en una solución ácida que contiene un exceso de KI. La reacción entre\(\text{IO}_3^-\) y yo —
\[\text{IO}_3^-(aq) + 8\text{I}^-(aq) + 6\text{H}^+(aq) \rightarrow 3\text{I}_3^-(aq) + 3\text{H}_2\text{O}(l) \nonumber\]
libera una cantidad estequiométrica de I-3. Al valorar esto\(\text{I}_3^-\) con tiosulfato, utilizando almidón como indicador visual, podemos determinar la concentración de\(\text{S}_2\text{O}_3^{2-}\) en el valorante.
La titulación de estandarización es
\[\text{I}_3^-(aq) + 2\text{S}_2\text{O}_3^{2-}(aq) \rightarrow 3\text{I}^-(aq) + \text{S}_4\text{O}_6^{2-}(aq) \nonumber\]
que es la misma reacción utilizada para estandarizar soluciones de\(\text{I}_3^-\). Este enfoque para estandarizar soluciones de\(\text{S}_2\text{O}_2^{3-}\) es similar al utilizado en la determinación del residuo de cloro total descrito en el Método Representativo 9.4.1.
Aunque el tiosulfato es uno de los pocos titulantes reductores que no se oxida fácilmente por contacto con el aire, está sujeto a una lenta descomposición en bisulfito y azufre elemental. Si se usa durante un periodo de varias semanas, se restandardiza periódicamente una solución de tiosulfato. Varias formas de bacterias son capaces de metabolizar el tiosulfato, lo que conduce a un cambio en su concentración. Este problema se minimiza al agregar un conservante como HgI 2 a la solución.
Otro valorante reductor útil es el sulfato de amonio ferroso, Fe (NH 4) 2 (SO 4) 2 •6H 2 O, en el que el hierro está presente en el estado de oxidación +2. Una solución de Fe 2 + es susceptible a la oxidación al aire, pero cuando se prepara en 0.5 M H 2 SO 4 permanece estable hasta un mes. Es recomendable la reandardización periódica con K 2 Cr 2 O 7. El sulfato de amonio ferroso se utiliza como valorante en un análisis directo del titrand, o bien, se agrega al título en exceso y la cantidad de Fe 3 + producida se determina por retrotitulación con una solución estándar de Ce 4 + o\(\text{Cr}_2\text{O}_7^{2-}\).
Análisis Inorgánico
Una de las aplicaciones más importantes de la titrimetría redox es evaluar la cloración de los suministros públicos de agua. El Método Representativo 9.4.1, por ejemplo, describe un enfoque para determinar el cloro residual total usando el poder oxidante del cloro para oxidar I — a\(\text{I}_3^-\). La cantidad de\(\text{I}_3^-\) se determina valorando de nuevo con\(\text{S}_2\text{O}_3^{2-}\).
La eficiencia de la cloración depende de la forma de las especies clorantes. Hay dos contribuciones al residuo de cloro total: el cloro residual libre y el residuo de cloro combinado. El residuo de cloro libre incluye formas de cloro que están disponibles para desinfectar el suministro de agua. Ejemplos de especies que contribuyen al residuo de cloro libre incluyen Cl 2, HOCl y OCl —. El cloro residual combinado incluye aquellas especies en las que el cloro está en su forma reducida y, por lo tanto, ya no es capaz de proporcionar desinfección. Las especies que contribuyen al cloro residual combinado son NH 2 Cl, NHCl 2 y NCl 3.
Cuando se mezcla una muestra de agua clorada libre de yoduro con un exceso del indicador N, N-dietil - p-fenilendiamina (DPD), el cloro libre oxida una porción estequiométrica de DPD a su forma de color rojo. El DPD oxidado se vuelve a valorar a su forma incolora usando sulfato de amonio ferroso como valorante. El volumen de valorante es proporcional al cloro residual libre.
Habiendo determinado el cloro libre residual en la muestra de agua, se agrega una pequeña cantidad de KI, que cataliza la reducción de monocloramina, NH 2 Cl, y oxida una porción del DPD de nuevo a su forma de color rojo. Al valorar el DPD oxidado con sulfato de amonio ferroso se obtiene la cantidad de NH 2 Cl en la muestra. La cantidad de dicloramina y tricloramina se determina de manera similar.
Los métodos descritos anteriormente para determinar el residuo de cloro total, libre o combinado también se utilizan para establecer la demanda de cloro de un suministro de agua. La demanda de cloro se define como la cantidad de cloro necesaria para reaccionar completamente con cualquier sustancia que pueda ser oxidada por el cloro, manteniendo al mismo tiempo el cloro residual deseado. Se determina añadiendo progresivamente mayores cantidades de cloro a un conjunto de muestras extraídas del suministro de agua y determinando el cloro residual total, libre o combinado.
Otro ejemplo importante de la titrimetría redox, que encuentra aplicaciones tanto en la salud pública como en el análisis ambiental, es la determinación del oxígeno disuelto. En aguas naturales, como lagos y ríos, el nivel de O 2 disuelto es importante por dos razones: es el oxidante más fácilmente disponible para la oxidación biológica de contaminantes inorgánicos y orgánicos; y es necesario para el soporte de la vida acuática. En una planta de tratamiento de aguas residuales disuelto O 2 es esencial para la oxidación aeróbica de materiales de desecho. Si la concentración de O 2 disuelto cae por debajo de un valor crítico, las bacterias aerobias son reemplazadas por bacterias anaerobias, y la oxidación de los desechos orgánicos produce gases indeseables, como CH 4 y H 2 S.
Un método estándar para determinar O 2 disuelto en aguas naturales y aguas residuales es el método Winkler. Se recolecta una muestra de agua sin exponerla a la atmósfera, lo que podría cambiar la concentración de O 2 disuelto. La muestra primero se trata con una solución de MnSO 4 y luego con una solución de NaOH y KI. En estas condiciones alcalinas el oxígeno disuelto oxida Mn 2 + a MnO 2.
\[2\text{Mn}^{2+}(aq) + 4\text{OH}^-(aq) + \text{O}_2(g) \rightarrow 2\text{MnO}_2(s) + 2\text{H}_2\text{O}(l) \nonumber\]
Una vez completada la reacción, la solución se acidifica con H 2 SO 4. Bajo las condiciones ahora ácidas, I — es oxidado\(\text{I}_3^-\) por MnO 2.
\[\text{MnO}_2(s) + 3\text{I}^-(aq) + 4\text{H}^+(aq) \rightarrow \text{Mn}^{2+}(aq) + \text{I}_3^-(aq) + 2\text{H}_2\text{O}(l) \nonumber\]
La cantidad de\(\text{I}_3^-\) esa forma se determina valorando con el\(\text{S}_2\text{O}_3^{2-}\) uso de almidón como indicador. El método Winkler está sujeto a una variedad de interferencias y se han propuesto varias modificaciones al procedimiento original. Por ejemplo,\(\text{NO}_2^-\) interfiere porque reduce\(\text{I}_3^-\) a I —bajo condiciones ácidas. Esta interferencia se elimina mediante la adición de azida sódica, NaN 3, que reduce\(\text{NO}_2^-\) a N 2. Otros agentes reductores, como Fe 2 +, se eliminan pretratando la muestra con KMnO 4 y destruyendo cualquier exceso de permanganato con K 2 C 2 O 4.
Otro ejemplo importante de la titrimetría redox es la determinación de agua en disolventes no acuosos. El valorante para este análisis se conoce como reactivo de Karl Fischer y consiste en una mezcla de yodo, dióxido de azufre, piridina y metanol. Debido a que la concentración de piridina es suficientemente grande, I 2 y SO 2 reaccionan con piridina (py) para formar los complejos Py•I 2 y Py•SO 2. Cuando se agrega a una muestra que contiene agua, I 2 se reduce a I — y SO 2 se oxida a SO 3.
\[\text{py}\cdot\text{I}_2 + \text{py}\cdot\text{SO}_2 + \text{H}_2\text{O} + 2\text{py} \rightarrow 2\text{py}\cdot\text{HI} + \text{py}\cdot\text{SO}_3 \nonumber\]
Se incluye metanol para evitar la reacción posterior de Py•SO 3 con agua. El punto final de la titulación se señala cuando la solución cambia del color amarillo del producto al color marrón del reactivo de Karl Fischer.
Análisis Orgánico
La titrimetría redox también se utiliza para el análisis de analitos orgánicos. Un ejemplo importante es la determinación de la demanda química de oxígeno (DQO) de aguas naturales y aguas residuales. La DQO es una medida de la cantidad de oxígeno necesaria para oxidar completamente toda la materia orgánica en una muestra a CO 2 y H 2 O. Debido a que no se intenta corregir la materia orgánica que se descompone biológicamente, o para la cinética de descomposición lenta, la DQO siempre sobreestima a la verdadera demanda de oxígeno de la muestra. La determinación de la DQO es particularmente importante en el manejo de las instalaciones industriales de tratamiento de aguas residuales donde se utiliza para monitorear la liberación de desechos ricos en orgánicos a los sistemas de alcantarillado municipal o al medio ambiente.
La DQO de una muestra se determina calentándola a reflujo en presencia de exceso de K 2 Cr 2 O 7, que sirve como agente oxidante. La solución se acidifica con H 2 SO 4, utilizando Ag 2 SO 4 para catalizar la oxidación de ácidos grasos de bajo peso molecular. Se agrega sulfato mercúrico, HGSO 4, para complejar cualquier cloruro que esté presente, lo que evita la precipitación del catalizador Ag + como AgCl. En estas condiciones, la eficiencia para oxidar la materia orgánica es del 95— 100%. Después de reflujo durante dos horas, la solución se enfría a temperatura ambiente y el exceso\(\text{Cr}_2\text{O}_7^{2-}\) se determina mediante una retrotitulación utilizando sulfato de amonio ferroso como valorante y ferroína como indicador. Debido a que es difícil eliminar completamente todas las trazas de materia orgánica de los reactivos, se realiza una titulación en blanco. La diferencia en la cantidad de sulfato de amonio ferroso necesario para valorar la muestra y el blanco es proporcional a la DQO.
El yodo se ha utilizado como un valorante oxidante para una serie de compuestos de interés farmacéutico. Anteriormente notamos que la reacción de\(\text{S}_2\text{O}_3^{2-}\) con\(\text{I}_3^-\) produce el ion tetrationato,\(\text{S}_4\text{O}_6^{2-}\). El ion tetrationato es en realidad un dímero que consiste en dos iones tiosulfato conectados a través de un enlace disulfuro (—S—S—). De la misma manera,\(\text{I}_3^-\) se utiliza para valorar mercaptanos de fórmula general RSH, formando el dímero RSSR como producto. El aminoácido cisteína también se puede valorar con\(\text{I}_3^-\). El producto de esta titulación es la cistina, que es un dímero de cisteína. El triyoduro también se utiliza para el análisis del ácido ascórbico (vitamina C) al oxidar el grupo funcional enediol a una alfa dicetona
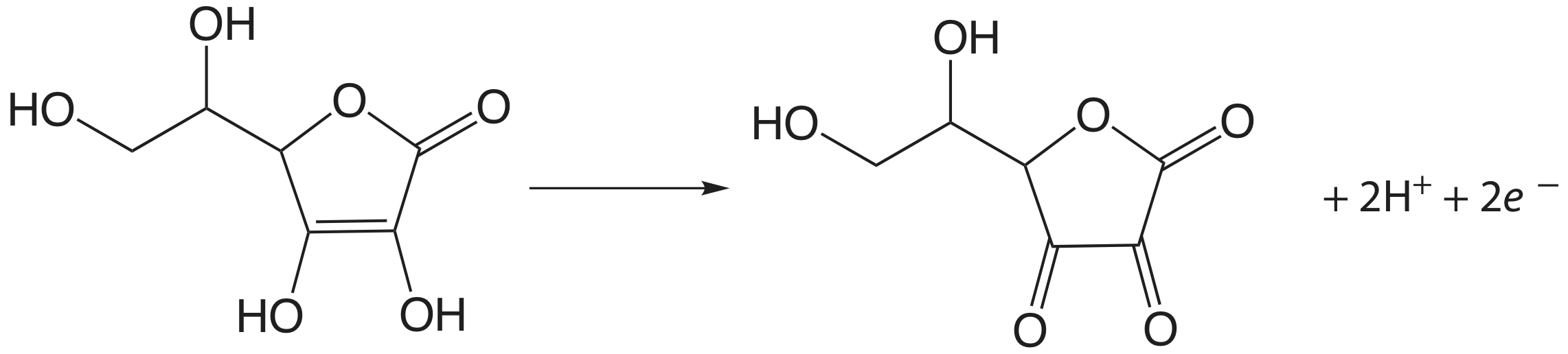
y para el análisis de azúcares reductores, como la glucosa, oxidando el grupo funcional aldehído a un ion carboxilato en una solución básica.
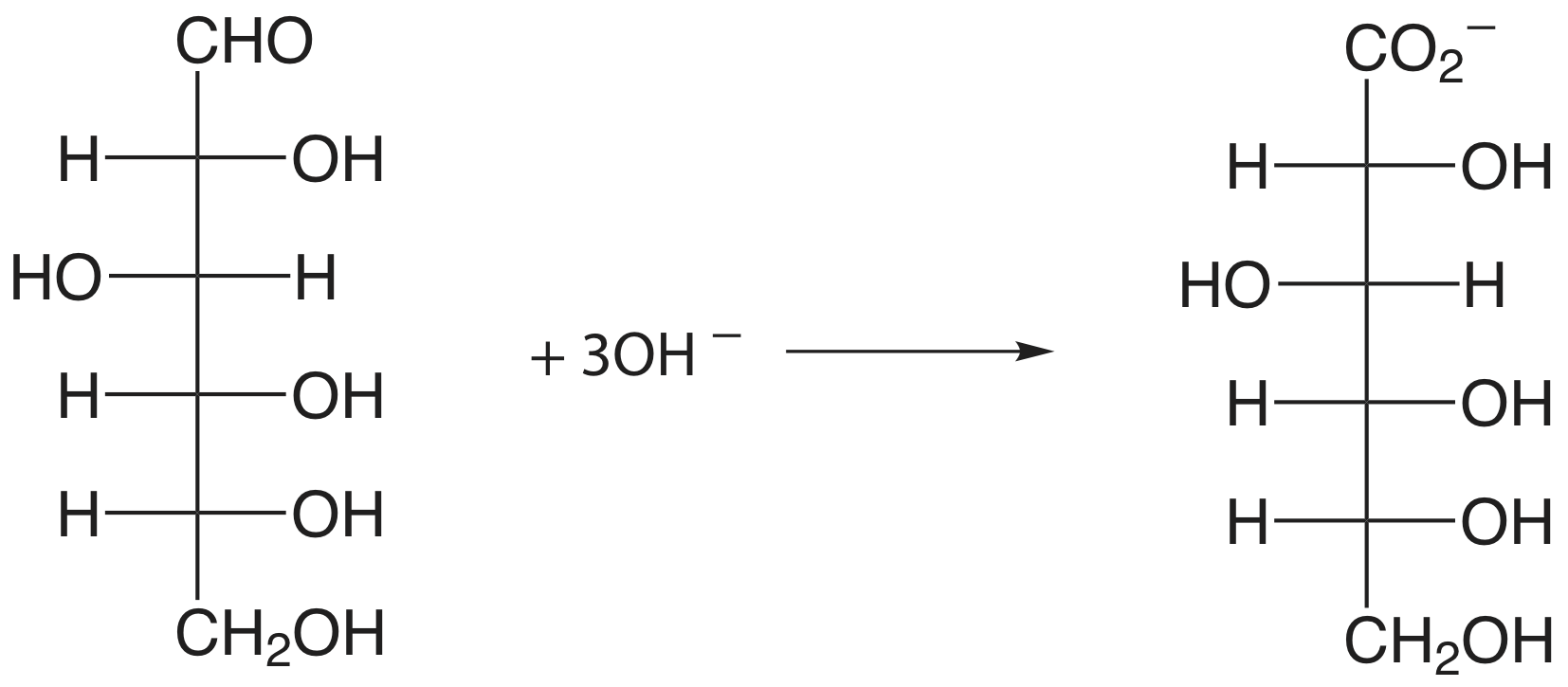
Un compuesto orgánico que contiene un grupo funcional hidroxilo, carbonilo o amina adyacente a un grupo hidoxilo o carbonilo se puede oxidar usando metaperyodato\(\text{IO}_4^-\),, como valorante oxidante.
\[\text{IO}_4^-(aq) + \text{H}_2\text{O}(l) + 2e^- \rightleftharpoons \text{IO}_3^-(aq) + 2\text{OH}^-(aq) \nonumber\]
Una oxidación de dos electrones escinde el enlace C-C entre los dos grupos funcionales con grupos hidroxilo oxidados a aldehídos o cetonas, grupos carbonilo oxidados a ácidos carboxílicos y aminas oxidadas a un aldehído y una amina (amoníaco si es una amina primaria). El análisis se realiza añadiendo un exceso conocido de\(\text{IO}_4^-\) a la solución que contiene el analito y permitiendo que la oxidación tenga lugar durante aproximadamente una hora a temperatura ambiente. Cuando se completa la oxidación, se agrega un exceso de KI, lo que convierte cualquier que no haya reaccionado\(\text{IO}_4^-\) en\(\text{IO}_3^-\) y\(\text{I}_3^-\).
\[\text{IO}_4^-(aq) + 3\text{I}^-(aq) + \text{H}_2\text{O}(l) \rightarrow \text{IO}_3^-(aq) + \text{I}_3^-(aq) + 2\text{OH}^-(aq) \nonumber\]
Luego\(\text{I}_3^-\) se determina valorando con el\(\text{S}_2\text{O}_3^{2-}\) uso de almidón como indicador.
Cálculos cuantitativos
La relación cuantitativa entre el valorador y el valorante está determinada por la estequiometría de la reacción de titulación. Si no estás seguro de la reacción equilibrada, puedes deducir su estequiometría recordando que los electrones en una reacción redox se conservan.
La cantidad de Fe en una muestra de 0.4891-g de un mineral se determina valorando con K 2 Cr 2 O 7. Después de disolver la muestra en HCl, el hierro se lleva a un estado de oxidación +2 usando un reductor Jones. La valoración al punto final del ácido difenilaminosulfónico requiere 36.92 mL de 0.02153 M K 2 Cr 2 O 7. Reporte el contenido de hierro del mineral como %w/w Fe 2 O 3.
Solución
Debido a que no se nos proporciona la reacción de titulación, utilizaremos una conservación de electrones para deducir la estequiometría. Durante la titulación el analito se oxida de Fe 2 + a Fe 3 +, y el valorante se reduce de\(\text{Cr}_2\text{O}_7^{2-}\) a Cr 3 +. Oxidar Fe 2 + a Fe 3 + requiere un solo electrón. La reducción\(\text{Cr}_2\text{O}_7^{2-}\), en la que cada cromo está en el estado de oxidación +6, a Cr 3+ requiere tres electrones por cromo, para un total de seis electrones. Una conservación de electrones para la titulación, por lo tanto, requiere que cada mol de K 2 Cr 2 O 7 reaccione con seis moles de Fe 2 +.
Los moles de K 2 Cr 2 O 7 utilizados para alcanzar el punto final son
\[(0.02153 \text{ M})(0.03692 \text{ L}) = 7.949 \times 10^{-4} \text{ mol K}_2\text{Cr}_2\text{O}_7 \nonumber\]
lo que significa que la muestra contiene
\[7.949 \times 10^{-4} \text{ mol K}_2\text{Cr}_2\text{O}_7 \times \frac{6 \text{ mol Fe}^{2+}}{\text{mol K}_2\text{Cr}_2\text{O}_7} = 4.769 \times 10^{-3} \text{ mol Fe}^{2+} \nonumber\]
Así, el% p/p de Fe 2 O 3 en la muestra de mineral es
\[4.769 \times 10^{-3} \text{ mol Fe}^{2+} \times \frac{1 \text{ mol Fe}_2\text{O}_3}{2 \text{ mol Fe}^{2+}} \times \frac{159.69 \text{g Fe}_2\text{O}_3}{\text{mol Fe}_2\text{O}_3} = 0.3808 \text{ g Fe}_2\text{O}_3 \nonumber\]
\[\frac{0.3808 \text{ g Fe}_2\text{O}_3}{0.4891 \text{ g sample}} \times 100 = 77.86 \text{% w/w Fe}_2\text{O}_3 \nonumber\]
Aunque podemos deducir la estequiometría entre el valorante y el valor en el Ejemplo 9.4.2 sin equilibrar la reacción de titulación, la reacción equilibrada
\[\text{K}_2\text{Cr}_2\text{O}_7(aq) + 6\text{Fe}^{2+}(aq) + 14\text{H}^+(aq) \rightarrow 2\text{Cr}^{3+}(aq) + 2\text{K}^+(aq) + 6\text{Fe}^{3+}(aq) + 7\text{H}_2\text{O}(l) \nonumber\]
proporciona información útil. Por ejemplo, la presencia de H + nos recuerda que la reacción debe realizarse en una solución ácida.
La pureza de una muestra de oxalato de sodio, Na 2 C 2 O 4, se determina valorando con una solución estándar de KMnO 4. Si una muestra de 0.5116-g requiere 35.62 mL de 0.0400 M KMnO 4 para alcanzar el punto final de la titulación, cuál es el% w/w de Na 2 C 2 O 4 en la muestra.
- Contestar
-
Debido a que no se nos proporciona una reacción equilibrada, usemos una conservación de electrones para deducir la estequiometría. Oxidante\(\text{C}_2\text{O}_4^{2-}\), en el que cada carbono tiene un estado de oxidación +3, a CO 2, en el que el carbono tiene un estado de oxidación de +4, requiere un electrón por carbono o un total de dos electrones por cada mol de\(\text{C}_2\text{O}_4^{2-}\). La reducción\(\text{MnO}_4^-\), en la que cada manganeso se encuentra en el estado de oxidación +7, a Mn 2 + requiere cinco electrones. Una conservación de electrones para la titulación, por lo tanto, requiere que dos moles de KMnO 4 (10 moles de e -) reaccionen con cinco moles de Na 2 C 2 O 4 (10 moles de e -).
Los moles de KMnO 4 utilizados para llegar al punto final son
\[(0.0400 \text{ M KMnO}_4)(0.03562 \text{ L})=1.42 \times 10^{-3} \text{ mol KMnO}_4 \nonumber\]
lo que significa que la muestra contiene
\[1 .42 \times 10^{-3} \text{ mol KMnO}_4 \times \frac{5 \text{ mol Na}_2\text{C}_2\text{O}_4}{2 \text{ mol KMnO}_4} = 3.55 \times 10^{-3} \text{ mol Na}_2\text{C}_2\text{O}_4 \nonumber\]
Así, el% p/p de Na 2 C 2 O 4 en la muestra de mineral es
\[3.55 \times 10^{-3} \text{ mol Na}_2\text{C}_2\text{O}_4 \times \frac{134.00 \text{ g Na}_2\text{C}_2\text{O}_4}{\text{mol Na}_2\text{C}_2\text{O}_4} = 0.476 \text{ g Na}_2\text{C}_2\text{O}_4 \nonumber\]
\[\frac{0.476 \text{ g Na}_2\text{C}_2\text{O}_4}{0.5116 \text{ g sample}} \times 100 = 93.0 \text{% w/w Na}_2\text{C}_2\text{O}_4 \nonumber\]
Como se muestra en los siguientes dos ejemplos, podemos extender fácilmente este enfoque a un análisis que requiera un análisis indirecto o una retrotitulación.
Una muestra de 25.00 ml de un blanqueador líquido se diluye a 1000 mL en un matraz aforado. Una porción de 25 ml de la muestra diluida se transfiere mediante pipeta a un matraz Erlenmeyer que contiene un exceso de KI, reduciendo el OCl — a Cl — y produciendo\(\text{I}_3^-\). El liberado\(\text{I}_3^-\) se determina valorando con 0.09892 M Na 2 S 2 O 3, requiriendo 8.96 mL para alcanzar el punto final del indicador de almidón. Reporte el% p/v de NaOCl en la muestra de lejía.
Solución
Para determinar la estequiometría entre el analito, NaOCl, y el valorante, Na 2 S 2 O 3, debemos considerar tanto la reacción entre OCl —e I —, como la valoración de\(\text{I}_3^-\) con Na 2 S 2 O 3.
Primero, en la reducción de OCl —a Cl — el estado de oxidación del cloro cambia de +1 a —1, requiriendo dos electrones. La oxidación de tres I —para formar\(\text{I}_3^-\) libera dos electrones a medida que el estado de oxidación de cada yodo cambia de —1 en I — a —1⁄3 pulgadas\(\text{I}_3^-\). Una conservación de electrones, por lo tanto, requiere que cada mol de OCl —produzca un mol de\(\text{I}_3^-\).
Segundo, en la reacción de titulación,\(\text{I}_3^-\) se reduce a I —y\(\text{S}_2\text{O}_3^{2-}\) se oxida a\(\text{S}_4\text{O}_6^{2-}\). Reducir\(\text{I}_3^-\) a 3I — requiere dos elecciones ya que cada yodo cambia de un estado de oxidación de —1⁄3 a —1. Al oxidar\(\text{S}_2\text{O}_3^{2-}\) a\(\text{S}_4\text{O}_6^{2-}\), cada azufre cambia su estado de oxidación de +2 a +2.5, liberando un electrón por cada uno\(\text{S}_2\text{O}_3^{2-}\). Una conservación de electrones, por lo tanto, requiere que cada mol de\(\text{I}_3^-\) reaccione con dos moles de\(\text{S}_2\text{O}_3^{2-}\).
Finalmente, debido a que cada mol de OCl — produce un mol de\(\text{I}_3^-\), y cada mol de\(\text{I}_3^-\) reacciona con dos moles de\(\text{S}_2\text{O}_3^{2-}\), sabemos que cada mol de NaOCl en la muestra finalmente resulta en el consumo de dos moles de Na 2 S 2 O 3.
Los moles de Na 2 S 2 O 3 utilizados para alcanzar el punto final de la titulación son
\[(0.09892 \text{ M})(0.00896 \text{ L}) = 8.86 \times 10^{-4} \text{ mol Na}_2\text{S}_2\text{O}_3 \nonumber\]
lo que significa que la muestra contiene
\[8.86 \times 10^{-4} \text{ mol Na}_2\text{S}_2\text{O}_3 \times \frac{1 \text{ mol NaOCl}}{\text{mol Na}_2\text{S}_2\text{O}_3} \times \frac{74.44 \text{ g NaOCl}}{\text{mol NaOCl}} = 0.03299 \text{ g NaOCl} \nonumber\]
Así, el% p/v de NaOCl en la muestra diluida es
\[\frac{0.03299 \text{ g NaOCl}}{25.00 \text{ mL}} \times 100 = 0.132 \text{% w/v NaOCl} \nonumber\]
Debido a que el blanqueador se diluyó por un factor de\(40 \times\) (25 mL a 1000 mL), la concentración de NaOCl en el blanqueador es de 5.28% p/v.
Las reacciones equilibradas para este análisis son:
\[\text{OCl}^-(aq) + 3\text{I}^-(aq) + 2\text{H}^+(aq) \rightarrow \text{I}_3^-(aq) + \text{Cl}^-(aq) + \text{H}_2\text{O}(l) \nonumber\]
\[\text{I}_3^-(aq) + 2\text{S}_2\text{O}_3^{2-}(aq) \rightarrow \text{S}_4\text{O}_6^{2-}(aq) + 3\text{I}^-(aq) \nonumber\]
La cantidad de ácido ascórbico, C 6 H 8 O 6, en el jugo de naranja se determina oxidando ácido ascórbico a ácido deshidroascórbico, C 6 H 6 O 6, con una cantidad conocida de\(\text{I}_3^-\), y retrotitulando el exceso\(\text{I}_3^-\) con Na 2 S 2 O 3. Se trata una muestra de 5.00-mL de jugo de naranja filtrado con 50.00 mL de 0.01023\(\text{I}_3^-\) M. Una vez completada la oxidación, se necesitan 13.82 mL de 0.07203 M Na 2 S 2 O 3 para alcanzar el punto final del indicador de almidón. Reporte la concentración de ácido ascórbico en mg/100 mL.
Solución
Para una retrotitulación necesitamos determinar la estequiometría entre\(\text{I}_3^-\) y el analito, C 6 H 8 O 6, y entre\(\text{I}_3^-\) y el valorante, Na 2 S 2 O 3. El último es fácil porque sabemos por Example 9.4.3 que cada mol de\(\text{I}_3^-\) reacciona con dos moles de Na 2 S 2 O 3.
Al oxidar ácido ascórbico a ácido deshidroascórbico, el estado de oxidación del carbono cambia de +2⁄3 en C 6 H 8 O 6 a +1 en C 6 H 6 O 6. Cada carbono libera 1⁄3 de un electrón, o un total de dos electrones por ácido ascórbico. Como aprendimos en Ejemplo 9.4.3 , la reducción\(\text{I}_3^-\) requiere de dos electrones; así, una conservación de electrones requiere que cada mol de ácido ascórbico consuma un mol de\(\text{I}_3^-\).
Los moles totales de los\(\text{I}_3^-\) que reaccionan con C 6 H 8 O 6 y con Na 2 S 2 O 3 es
\[(0.01023 \text{ M})(0.05000 \text{ L}) = 5.115 \times 10^{-4} \text{ mol I}_3^- \nonumber\]
La valoración posterior consume
\[0.01382 \text{ L Na}_2\text{S}_2\text{O}_3 \times \frac{0.07203 \text{ mol Na}_2\text{S}_2\text{O}_3}{\text{ L Na}_2\text{S}_2\text{O}_3} \times \frac{1 \text{ mol I}_3^-}{2 \text{ mol Na}_2\text{S}_2\text{O}_3} = 4.977 \times 10^{-4} \text{ mol I}_3^- \nonumber\]
Restar los moles de los\(\text{I}_3^-\) que reaccionan con Na 2 S 2 O 3 del total de moles\(\text{I}_3^-\) da los moles que reaccionan con ácido ascórbico.
\[5.115 \times 10^{-4} \text{ mol I}_3^- - 4.977 \times 10^{-4} \text{ mol I}_3^- = 1.38 \times 10^{-5} \text{ mol I}_3^- \nonumber\]
Los gramos de ácido ascórbico en la muestra de 5.00-mL de jugo de naranja es
\[1.38 \times 10^{-5} \text{ mol I}_3^- \times \frac{1 \text{ mol C}_6\text{H}_8\text{O}_6}{\text{mol I}_3^-} \times \frac{176.12 \text{ g C}_6\text{H}_8\text{O}_6}{\text{mol C}_6\text{H}_8\text{O}_6} = 2.43 \times 10^{-3} \text{ g C}_6\text{H}_8\text{O}_6 \nonumber\]
Hay 2.43 mg de ácido ascórbico en la muestra de 5.00-mL, o 48.6 mg por cada 100 mL de jugo de naranja.
Las reacciones equilibradas para este análisis son:
\[\text{C}_6\text{H}_8\text{O}_6(aq) + \text{I}_3^- (aq) \rightarrow 3\text{I}^-(aq) + \text{C}_6\text{H}_6\text{O}_6(aq) + 2\text{H}^+(aq) \nonumber\]
\[\text{I}_3^-(aq) + 2\text{S}_2\text{O}_3^{2-}(aq) \rightarrow \text{S}_4\text{O}_6^{2-}(aq) + 3\text{I}^-(aq) \nonumber\]
Se realiza un análisis cuantitativo para etanol, C 2 H 6 O, mediante una retrovaloración redox. El etanol se oxida a ácido acético, C 2 H 4 O 2, utilizando dicromato en exceso\(\text{Cr}_2\text{O}_7^{2-}\), el cual se reduce a Cr 3 +. El exceso de dicromato se titula con Fe 2 +, dando como productos Cr 3 + y Fe 3 +. En un análisis típico, una muestra de 5.00-mL de un brandy se diluye a 500 mL en un matraz aforado. Se toma una muestra de 10.00 mL y el etanol se retira por destilación y se recoge en 50.00 mL de una solución acidificada de 0.0200 M K 2 Cr 2 O7. Una retrovaloración del no reaccionado\(\text{Cr}_2\text{O}_7^{2-}\) requiere 21.48 mL de 0.1014 M Fe 2 +. Calcular el% p/v de etanol en el brandy.
- Contestar
-
Para una retrotitulación necesitamos determinar la estequiometría entre\(\text{Cr}_2\text{O}_7^{2-}\) y el analito, C 2 H 6 O, y entre\(\text{Cr}_2\text{O}_7^{2-}\) y el valorante, Fe 2 +. Al oxidar etanol a ácido acético, el estado de oxidación del carbono cambia de —2 en C 2 H 6 O a 0 en C 2 H 4 O 2. Cada carbono libera dos electrones, o un total de cuatro electrones por C 2 H 6 O. En reducción\(\text{Cr}_2\text{O}_7^{2-}\), en la que cada cromo tiene un estado de oxidación de +6, a Cr 3 +, cada cromo pierde tres electrones, para un total de seis electrones por\(\text{Cr}_2\text{O}_7^{2-}\). La oxidación de Fe 2 + a Fe 3 + requiere un electrón. Una conservación de electrones requiere que cada mol de K 2 Cr 2 O 7 (6 moles de e —) reaccione con seis moles de Fe 2 + (6 moles de e —), y que cuatro moles de K 2 Cr 2 O 7 (24 moles de e —) reaccionan con seis moles de C 2 H 6 O (24 moles de e —).
El total de moles de K 2 Cr 2 O 7 que reaccionan con C 2 H 6 O y con Fe 2 + es
\[(0.0200 \text{ M K}_2\text{Cr}_2\text{O}_7)(0.05000 \text{ L})=1.00 \times 10^{-3} \text{ mol K}_2\text{Cr}_2\text{O}_7 \nonumber\]
La valoración posterior con Fe 2 + consume
\[(0.1014 \text{ M Fe}^{2+})(0.02148 \text{ L}) \times \frac{1 \text{ mol K}_2\text{Cr}_2\text{O}_7}{6 \text{ mol Fe}^{2+}} = 3.63 \times 10^{-4} \text{ mol K}_2\text{Cr}_2\text{O}_7 \nonumber\]
Restar los moles de K 2 Cr 2 O 7 que reaccionan con Fe 2 + de los moles totales de K 2 Cr 2 O 7 da los moles que reaccionan con el analito.
\[(1.00 \times 10^{-3} \text{ mol K}_2\text{Cr}_2\text{O}_7) - (3.63 \times 10^{-4} \text{ mol K}_2\text{Cr}_2\text{O}_7) = 6.37 \times 10^{-4} \text{ mol K}_2\text{Cr}_2\text{O}_7 \nonumber\]
Los gramos de etanol en la muestra de 10.00-mL de brandy diluido es
\[6.37 \times 10^{-4} \text{ mol K}_2\text{Cr}_2\text{O}_7 \times \frac{6 \text{ mol C}_2\text{H}_6\text{O}}{4 \text{ mol K}_2\text{Cr}_2\text{O}_7} \times \frac{46.07 \text{ g C}_2\text{H}_6\text{O}}{\text{mol C}_2\text{H}_6\text{O}} = 0.0440 \text{ g C}_2\text{H}_6\text{O} \nonumber\]
El %p/v C 2 H 6 O en el brandy es
\[\frac{0.0440 \text{ g C}_2\text{H}_6\text{O}}{10.0 \text{ mL diluted brandy}} \times \frac{500.0 \text{ mL diluted brandy}}{5.00 \text{ mL brandy}} \times 100 = 44.0 \text{% w/v C}_2\text{H}_6\text{O} \nonumber\]
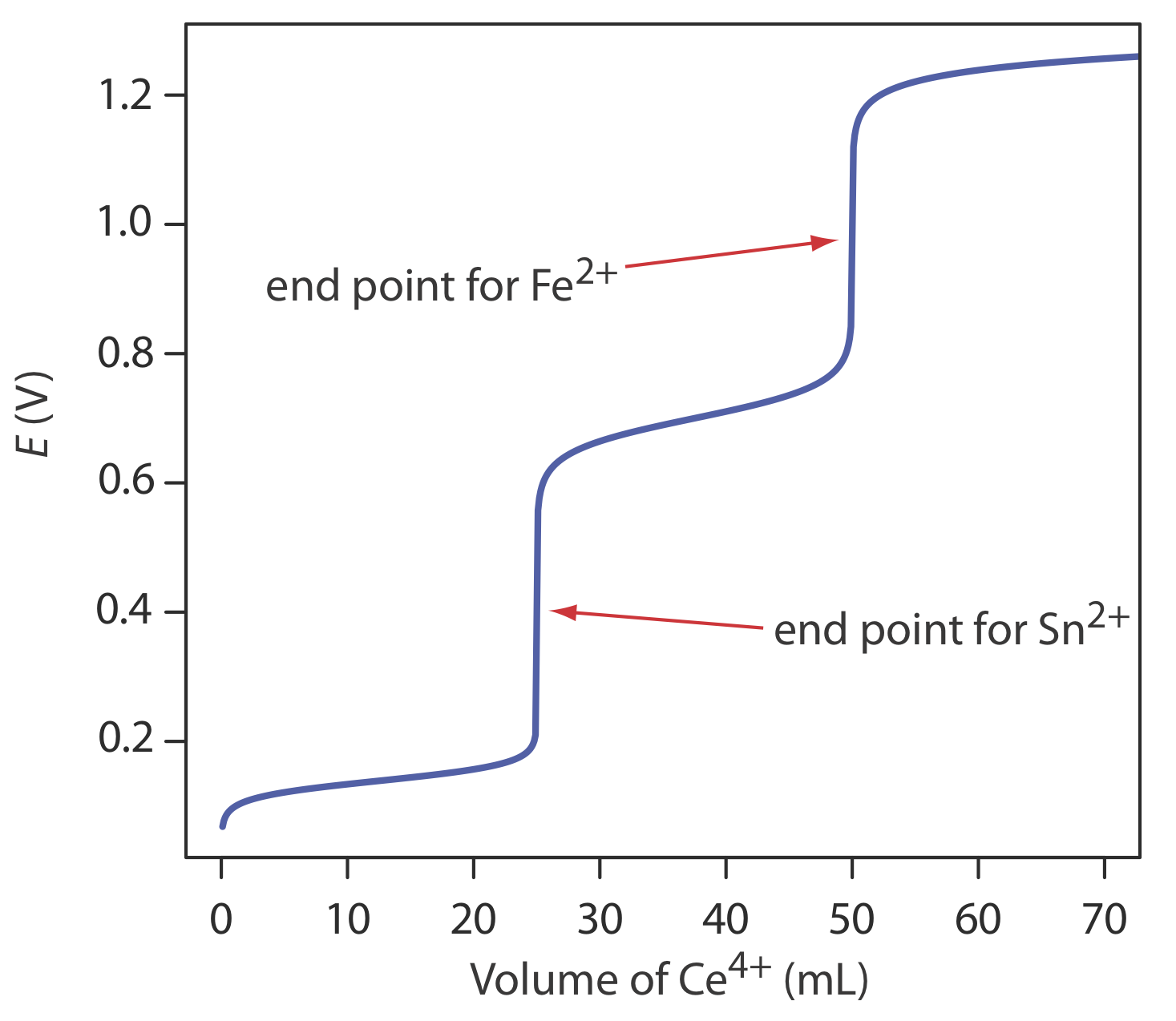
Evaluación de la Titrimetría Redox
La escala de operaciones, precisión, precisión, sensibilidad, tiempo y costo de una valoración redox son similares a las descritas anteriormente en este capítulo para una valoración ácido-base o de complejación. Al igual que con una valoración ácido-base, podemos extender una valoración redox al análisis de una mezcla de analitos si hay una diferencia significativa en sus potenciales de oxidación o reducción. La Figura 9.4.7 muestra un ejemplo de la curva de titulación para una mezcla de Fe 2 + y Sn 2 + usando Ce 4 + como valorante. Una valoración de una mezcla de analitos es posible si sus potenciales de estado estándar o potenciales formales difieren en al menos 200 mV.
