10.4: Una breve introducción a la probabilidad

Hemos hablado del hecho de que la función de onda puede interpretarse como una probabilidad, pero este es un buen momento para formalizar algunos conceptos y entender lo que realmente queremos decir con eso.

Empecemos por revisar (o aprender) algunos conceptos en teoría de probabilidad. En primer lugar, una variable aleatoria es una variable cuyo valor está sujeto a variaciones por casualidad. Por ejemplo, podríamos definir una variable que iguale el número de días que llueve en Phoenix cada mes, o el resultado de lanzar un dado (el número de puntos hacia arriba), o el tiempo que tarda el próximo autobús en llegar a la estación de autobuses, o el tiempo de espera que tendremos que aguantar la próxima vez que llamemos a un cliente línea telefónica de servicio. Algunas de estas variables aleatorias son discretas; el número de días de lluvia o el número de puntos que miran hacia arriba en un dado pueden tomar solo un número contable de valores distintos. Para el caso del dado, el resultado sólo puede ser\(\{1,2,3,4,5,6\}\). En contraste, un tiempo de espera es una variable aleatoria continua. Si pudieras medir con suficiente precisión, la variable aleatoria puede tomar cualquier valor real positivo. Volviendo a la química física, la posición de un electrón en un átomo o molécula es un buen ejemplo de una variable aleatoria continua.

Imagina un juego (ciertamente tonto) que implica voltear dos monedas. Obtienes un punto por cada cola, y dos puntos por cada cabeza. El juego tiene tres posibles resultados: 2 puntos (si consigues dos colas), 3 puntos (si consigues una cola y una cabeza) y 4 puntos (si consigues dos cabezas). Los resultados no tienen la misma probabilidad. La probabilidad de obtener dos cabezas o dos colas es 1/4, mientras que la probabilidad de que consigas una cabeza y una cola es 1/2. Si definimos una variable aleatoria (\(x\)) que es igual al número de puntos que obtienes en una ronda del juego, podemos representar las probabilidades de obtener cada resultado posible como:

\(x\)	2	3	4
\(P(x)\)	1/4	1/2	1/4

La colección de resultados se denomina espacio muestral. En este caso, el espacio muestral es\(\{2,3,4\}\). Si sumamos\(P(x)\) sobre el espacio muestral obtenemos, como se esperaba, 1. En otras palabras, la probabilidad de que obtengas un resultado que pertenezca al espacio muestral necesita ser 1, lo cual tiene sentido porque definimos el espacio muestral como la colección de todos los resultados posibles. Si piensas en un electrón en un átomo, y definimos la posición en coordenadas polares,\(r\) (la distancia desde el núcleo del átomo) es una variable aleatoria que puede tomar cualquier valor de 0 a\(\infty\). El espacio muestral para la variable aleatoria\(r\) es el conjunto de números reales positivos.

Volviendo a nuestra variable discreta\(x\), nuestro argumento anterior se traduce en

\[\sum\limits_{sample\; space}P(x)=1 \nonumber\]

¿Podemos medir las probabilidades? No exactamente, pero podemos medir la frecuencia de cada resultado si repetimos el experimento una gran cantidad de veces. Por ejemplo, si jugamos a este juego tres veces, no sabemos cuántas veces conseguiremos 2, 3 o 4 puntos. Pero si jugamos el juego un número muy grande de veces, sabemos que la mitad del tiempo conseguiremos 3 puntos, una cuarta parte del tiempo conseguirá 2 puntos, y otro cuarto 4 puntos. La probabilidad es la frecuencia de un resultado en el límite de un número infinito de ensayos. Formalmente, la frecuencia se define como el número de veces que obtiene un resultado determinado dividido para el número total de ensayos.

Ahora bien, aunque no tengamos forma de predecir el resultado de nuestro experimento aleatorio (el juego tonto que describimos anteriormente), si tuvieras que apostar, no lo pensarías dos veces y apostarías por\(x=3\) (una cabeza y una cola). El hecho de que una variable aleatoria no tenga un resultado predecible no significa que no tengamos información sobre la distribución de probabilidades. Volviendo a nuestro átomo, podremos predecir el valor de\(r\) al que la probabilidad de encontrar el electrón es más alta, el valor promedio de\(r\), etc. aunque sepamos que\(r\) puede tomar valores hasta\(\infty\), sabemos que es mucho más probable que lo encuentre muy cerca de la núcleo (por ejemplo, dentro de un ángulo) que lejos (por ejemplo, una pulgada). Ninguna ley física prohíbe que el electrón esté a 1 pulgada del núcleo, pero la probabilidad de que eso suceda es tan pequeña, que ni siquiera pensamos en esta posibilidad.

La media de una distribución discreta

Hablemos de la media (o promedio) un poco más. ¿Cuál es exactamente el promedio de una variable aleatoria? Volviendo a nuestro “juego”, sería el valor promedio que\(x\) obtendrías si pudieras jugar al juego un número infinito de veces. También podrías pedirle a todo el planeta que juegue el juego una vez, y eso lograría lo mismo. El planeta no tiene un número infinito de personas, pero el promedio que obtienes con varios miles de millones de pruebas del experimento aleatorio (lanzar dos monedas) debería estar bastante cerca del promedio real. Denotaremos el promedio (también llamado la media) con corchetes angulares:\(\left \langle x \right \rangle\). Digamos que jugamos a este juego\(10^9\) veces. Esperamos 3 puntos la mitad del tiempo (frecuencia =\(1/2\)), o en este caso,\(5\times 10^8\) tiempos. También esperamos 2 puntos o 4 puntos con una frecuencia de\(1/4\), entonces en este caso,\(2.5 \times 10^8\) tiempos. ¿Cuál es el promedio?

\[\left \langle x \right \rangle=\dfrac{1}{4}\times 2+\dfrac{1}{2}\times 3+\dfrac{1}{4}\times 4=3 \nonumber\]

En promedio, los mil millones de personas que juegan el juego (o tú lo juegas mil millones de veces) deberían obtener 3 puntos. Este pasa a ser el resultado más probable, pero no necesita ser el caso. Por ejemplo, si solo volteas una moneda, puedes obtener 1 punto o 2 puntos con igual probabilidad, y el promedio será de 1.5, que no es el resultado más probable. De hecho, ¡ni siquiera es un resultado posible!.

En general, debería tener sentido que para una variable discreta:

\[\label{eq:mean_discrete} \left \langle x \right \rangle=\sum\limits_{i=1}^k P(x_i)x_i\]

donde la suma se realiza sobre todo el espacio muestral, que contiene\(k\) elementos. Aquí,\(x_i\) está cada resultado posible, y\(P(x_i)\) es la probabilidad de obtener ese resultado (o la fracción de veces que lo obtendrías si realizaras una gran cantidad de ensayos).

Variables continuas

¿Cómo traducimos todo lo que acabamos de decir a una variable continua? Como ejemplo, volvamos a la variable aleatoria\(r\), que se define como la distancia del electrón en el átomo de hidrógeno desde su núcleo. Como veremos en breve, el electrón 1s en el átomo de hidrógeno pasa la mayor parte de su tiempo dentro de un par de angstroms del núcleo. Podemos preguntarnos, ¿cuál es la probabilidad de que el electrón se encuentre exactamente a 1Å del núcleo? Matemáticamente, ¿qué es\(P(r=1\) Å)? La respuesta te decepcionará, pero esta probabilidad es cero, y es cero para cualquier valor de\(r\). El electrón necesita estar en alguna parte, pero la probabilidad de encontrarle un valor particular de\(r\) es cero? Sí, ese es precisamente el caso, y es consecuencia de\(r\) ser una variable continua. Imagina que obtienes un número real aleatorio en el intervalo [0,1] (podrías hacer esto incluso en tu calculadora), y te pregunto cuál es la probabilidad de que obtengas exactamente\(\pi/4\). Hay infinitos números reales en este intervalo, y todos ellos son igualmente probables, por lo que la probabilidad de obtener cada uno de ellos es\(1/\infty=0\). Hablar de las probabilidades de resultados particulares no es muy útil en el contexto de variables continuas. Todos los resultados tienen una probabilidad de cero, aunque intuitivamente sabemos que la probabilidad de encontrar el electrón dentro de 1Å es mucho mayor que la probabilidad de encontrarlo a varias millas. En cambio, hablaremos de la densidad de probabilidad (\(p(r)\)). Si estás confundido acerca de por qué la probabilidad de un resultado en particular es cero revisa el video listado al final de esta sección.

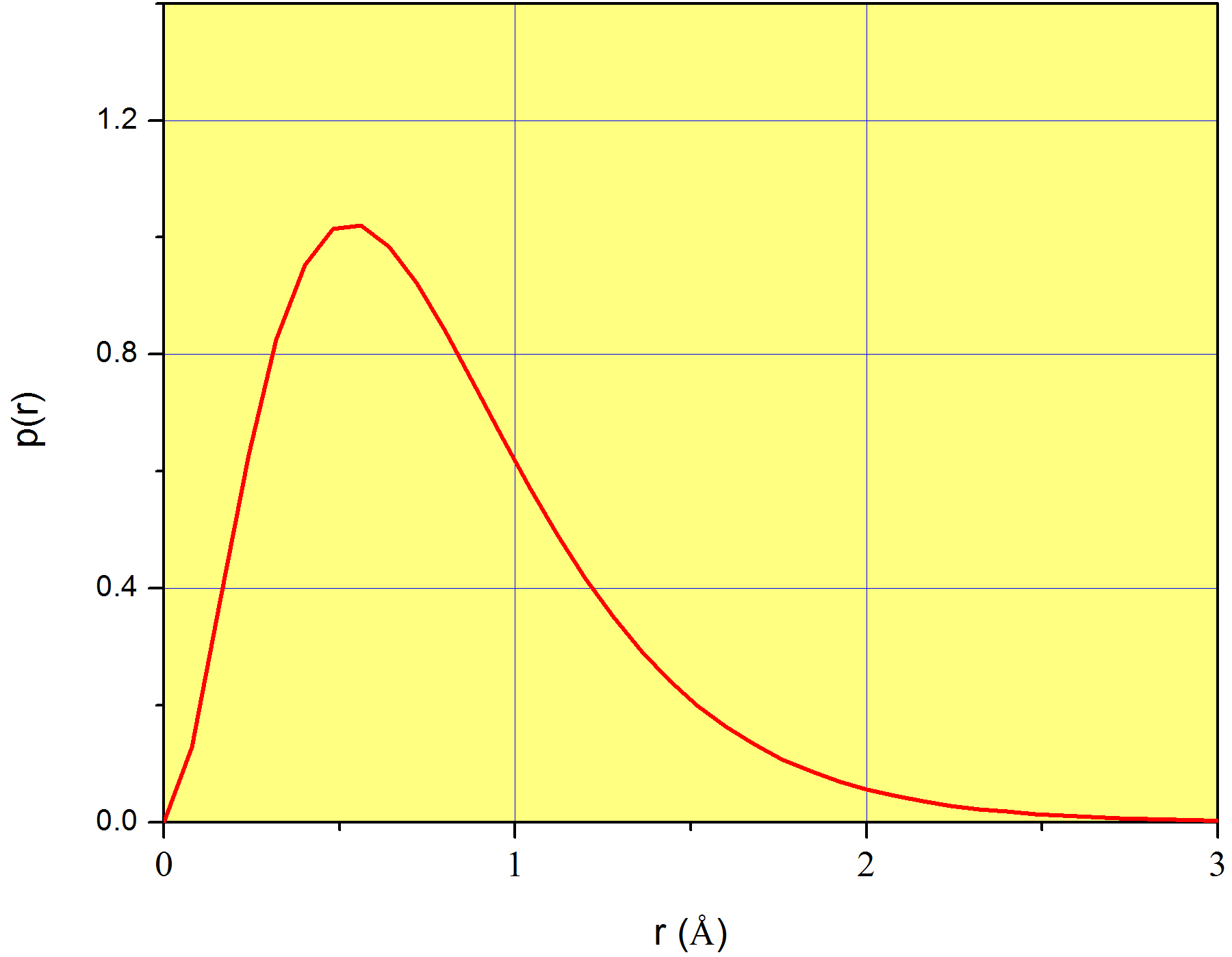
\(p(r)\)Se muestra una gráfica de en la Figura\(\PageIndex{1}\) para el caso del orbital 1s del átomo de hidrógeno. Nuevamente, enfatizamos que\(p(r)\) no mide la probabilidad correspondiente a cada valor de\(r\) (que es cero para todos los valores de\(r\)), sino que mide una densidad de probabilidad. Ya presentamos esta idea en la página

Figura\(\PageIndex{1}\): Función de densidad radial (\(p(r)\)) para el orbital 1s del átomo de hidrógeno (CC BY-NC-SA; Marcia Levitus)

Formalmente, la función de densidad de probabilidad (\(p(r)\)), se define de esta manera:

\[\label{eq:coordinates_pdf} P(a\leq r\leq b)=\int\limits_{a}^{b}p(r)dr\]

Esto significa que la probabilidad de que la variable aleatoria\(r\) tome un valor en el intervalo\([a,b]\) es la integral de la función de densidad de probabilidad de\(a\) a\(b\). Para un intervalo muy pequeño:

\[\label{eq:coordinates_pdf2} P(a\leq r\leq a+dr)=p(a)dr\]

En conclusión, aunque\(p(r)\) por sí sola no significa nada físicamente,\(p(r)dr\) es la probabilidad de que la variable\(r\) tome un valor en el intervalo entre\(r\) y\(r+dr\). Por ejemplo, volviendo a la Figura\(\PageIndex{1}\),\(p(1\) Å) = 0.62, lo que no significa en absoluto que 62% de las veces encontraremos el electrón exactamente a 1Å del núcleo. En cambio, podemos usarlo para calcular la probabilidad de que el electrón se encuentre en una región muy estrecha alrededor de 1Å. Por ejemplo,\(P(1\leq r\leq 1.001)\approx 0.62\times 0.001=6.2\times 10^{-4}\). Esto es sólo una aproximación porque el número 0.001, aunque mucho menor que 1, no es un infinitesimal.

En general, el concepto de función de densidad de probabilidad es más fácil de entender en el contexto de la Ecuación\ ref {eq:coordinates_pdf}. Se puede calcular la probabilidad de que el electrón se encuentre a una distancia menor que 1Å como:

\[P(0\leq r\leq 1)=\int\limits_{0}^{1}p(r)dr \nonumber\]

y a una distancia mayor que 1Å pero menor que 2Å como

\[P(1\leq r\leq 2)=\int\limits_{1}^{2}p(r)dr \nonumber\]

Por supuesto, la probabilidad de que el electrón esté en algún lugar del universo es 1, entonces:

\[P(0\leq r\leq \infty)=\int\limits_{0}^{\infty}p(r)dr=1 \nonumber\]

Aún no hemos escrito\(p(r)\) explícitamente, pero lo haremos en breve para que podamos realizar todas estas integraciones y obtener las probabilidades discutidas anteriormente.

Confundido acerca de las funciones continuas de densidad de probabilidad ¡Este video puede ayudar! http: //tinyurl.com/m6tgoap

La media de una distribución continua

Para una variable aleatoria continua\(x\), la ecuación\ ref {eq:mean_discrete} se convierte en:

\[\label{eq:mean_continuous} \left \langle x \right \rangle = \int\limits_{all\,outcomes}p(x) x \;dx\]

Volviendo a nuestro átomo:

\[\label{eq:mean_r} \left \langle r \right \rangle = \int\limits_{0}^{\infty}p(r) r \;dr\]

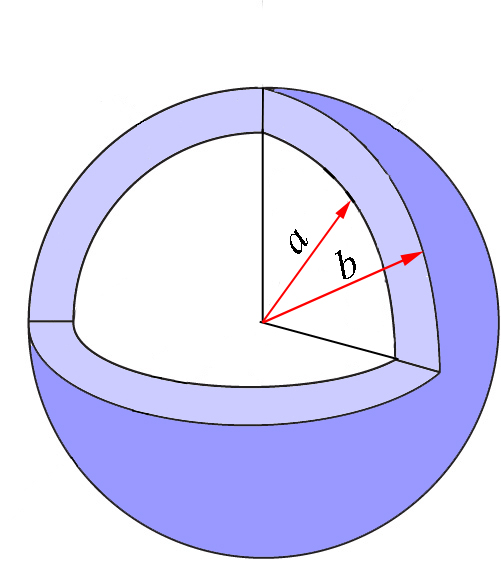
Nuevamente, volveremos a esta ecuación una vez que obtengamos la expresión para\(p(r)\) que necesitamos. Pero antes de hacerlo, vamos a ampliar esta discusión a más variables. Hasta el momento, hemos limitado nuestra discusión a una coordenada, por lo que la cantidad\(P(a\leq r\leq b)=\int\limits_{a}^{b}p(r)dr\) representa la probabilidad de que la coordenada\(r\) tome un valor entre\(a\) y\(b\), independientemente de los valores de\(\theta\) y\(\phi\). Esta región del espacio es la concha esférica representada en la Figura\(\PageIndex{2}\) en azul claro. Las esferas en la figura están cortadas para mayor claridad, pero por supuesto nos referimos a toda la concha que se define como la región entre dos esferas concéntricas de radios\(a\) y\(b\).

Figura\(\PageIndex{2}\): Una concha esférica (CC BY-NC-SA; Marcia Levitus)

¿Y si también nos interesan los ángulos? Digamos que queremos la probabilidad de que el electrón se encuentre entre\(r_1\) y\(r_2\),\(\theta_1\) y\(\theta_2\), y y\(\phi_1\) y\(\phi_2\). Este volumen se muestra en la Figura\(\PageIndex{3}\). La probabilidad que nos interesa es:

\[P(r_1\leq r\leq r_2, \theta_1\leq \theta \leq \theta_2, \phi_1 \leq \phi \leq\phi_2)=\int\limits_{\phi_1}^{\phi_2}\int\limits_{\theta_1}^{\theta_2}\int\limits_{r_1}^{r_2}p(r,\theta,\phi)\;r^2 \sin\theta dr d\theta d\phi \nonumber\]

Figura\(\PageIndex{3}\): Un volumen delimitado por las coordenadas\(r\) y\(r+\Delta r\),\(\theta\) y\(\theta+\Delta \theta\), y\(\phi\) y\(\phi+\Delta \phi\), (CC BY-NC-SA; Marcia Levitus)

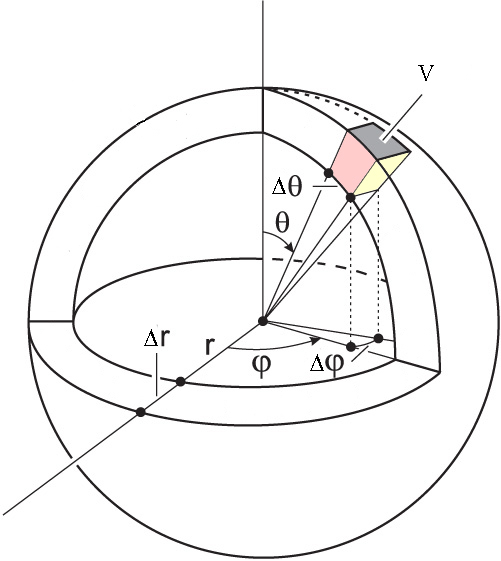
Observe que nos estamos integrando en coordenadas esféricas, por lo que necesitamos usar el diferencial de volumen correspondiente.

Esta función de densidad de probabilidad,\(p(r,\theta,\phi)\), es exactamente lo que\(|\psi(r,\theta,\phi)|^2\) representa! Por eso hemos estado diciendo que\(|\psi(r,\theta,\phi)|^2\) es una densidad de probabilidad. La función\(|\psi(r,\theta,\phi)|^2\) no representa una probabilidad en sí misma, sino que lo hace cuando se integra entre los límites de interés. Supongamos que queremos saber la probabilidad de que el electrón en el orbital 1s del átomo de hidrógeno se encuentre entre\(r_1\) y\(r_2\),\(\theta_1\) y\(\theta_2\), y\(\phi_1\) y\(\phi_2\). La respuesta a esta pregunta es:

\[\int\limits_{\phi_1}^{\phi_2}\int\limits_{\theta_1}^{\theta_2}\int\limits_{r_1}^{r_2}|\psi_{1s}|^2\;r^2 \sin\theta dr d\theta d\phi \nonumber\]

Volviendo al caso mostrado en la Figura\(\PageIndex{2}\), la probabilidad que\(r\) toma un valor entre\(a\) e\(b\) independientemente de los valores de los ángulos, es la probabilidad que\(r\) se encuentra entre\(a\) y\(b\), y\(\theta\) toma un valor entre 0 y\(\pi\), y\(\phi\) toma un valor entre 0 y\(2\pi\):

\[\label{eq:coordinates9} P(a\leq r\leq b)=P(a\leq r\leq b,0 \leq \theta \leq \pi, 0 \leq \phi \leq 2\pi)=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{a}^{b}|\psi_{1s}|^2\;r^2 \sin\theta dr d\theta d\phi\]

La función de densidad radial

Hasta ahora establecimos que\(|\psi(r,\theta,\phi)|^2\) es una función de densidad de probabilidad en coordenadas esféricas. Podemos realizar triples integrales para calcular la probabilidad de encontrar el electrón en diferentes regiones del espacio (¡pero no en un punto en particular!). A menudo es útil conocer la probabilidad de encontrar el electrón en un orbital a cualquier distancia dada del núcleo. Esto nos permite decir a qué distancia del núcleo es más probable que se encuentre el electrón, y también cuán apretada o floja está unido el electrón en un átomo en particular. Esto se expresa por la función de distribución radial\(p(r)\), que se representa gráficamente en la Figura\(\PageIndex{1}\) para el orbital 1s del átomo de hidrógeno.

En otras palabras, queremos que una versión de\(|\psi(r,\theta,\phi)|^2\) eso sea independiente de los ángulos. Esta nueva función será una función de\(r\) solo, y puede ser utilizada, entre otras cosas, para calcular la media de\(r\), el valor más probable de\(r\), la probabilidad que\(r\) se encuentra en un rango dado de distancias, etc.

Ya introdujimos esta función en la Ecuación\ ref {eq:coordinates_pdf}. La pregunta ahora es, ¿cómo obtenemos\(p(r)\) de\(|\psi(r,\theta,\phi)|^2\)? Comparemos la Ecuación\ ref {eq:coordinates_pdf} con la Ecuación\ ref {eq:coordinadas9}:

\[P(a\leq r\leq b)=\int\limits_{a}^{b}p(r)dr \nonumber\]

\[P(a\leq r\leq b)=P(a\leq r\leq b,0 \leq \theta \leq \pi, 0 \leq \phi \leq 2\pi)=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{a}^{b}|\psi(r,\theta,\phi)|^2\;r^2 \sin\theta dr d\theta d\phi \nonumber\]

Concluimos que

\[\int\limits_{a}^{b}p(r)dr=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{a}^{b}|\psi(r,\theta,\phi)|^2\;r^2 \sin\theta dr d\theta d\phi \nonumber\]

Todos los\(s\) orbitales son funciones reales de\(r\) solo, por lo que\(|\psi(r,\theta,\phi)|^2\) no depende de\(\theta\) ni\(\phi\). En este caso:

\[\int\limits_{a}^{b}p(r)dr=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{a}^{b}\psi^2(r)\;r^2 \sin\theta dr d\theta d\phi=\int\limits_{0}^{2\pi}d\phi \int\limits_{0}^{\pi}\sin\theta \;d\theta \int\limits_{a}^{b}\psi^2(r)\;r^2 dr=4\pi\int\limits_{a}^{b}\psi^2(r)\;r^2 dr \nonumber\]

Por lo tanto, para una\(s\) órbita,

\[p(r)=4\pi\psi^2(r)\;r^2 \nonumber\]

Por ejemplo, la función de onda normalizada del orbital 1s es la solución del Ejemplo\(10.1\):\(\dfrac{1}{\sqrt{\pi a_0^3}}e^{-r/a_0}\). Por lo tanto, para el orbital 1s:

\[\label{eq:coordinates10} p(r)=\dfrac{4}{a_0^3}r^2e^{-2r/a_0}\]

La ecuación\ ref {eq:coordinates10} se traza en la Figura\(\PageIndex{1}\). Para crear esta gráfica, necesitamos el valor de\(a_0\), que es una constante conocida como radio de Bohr, e igual\(5.29\times10^{-11}m\) (o 0.526 Å). Mira la posición del máximo de\(p(r)\); está ligeramente por encima de 0.5Å y más precisamente, ¡exactamente a\(r=a_0\)! Ahora bien queda claro por qué\(a_0\) se conoce como radio: es la distancia desde el núcleo a la que es mayor encontrar el único electrón del átomo de hidrógeno. En cierto modo,\(a_0\) es el radio del átomo, aunque sabemos que esto no es estrictamente cierto porque el electrón no está orbitando a un fijo\(r\) como los científicos creían hace mucho tiempo.

En general, para cualquier tipo de orbital,

\[\int\limits_{a}^{b}p(r)dr=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{a}^{b}|\psi(r,\theta,\phi)|^2\;r^2 \sin\theta dr d\theta d\phi=\int\limits_{a}^{b}{\color{Red}\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}|\psi(r,\theta,\phi)|^2\;r^2 \sin\theta\; d\theta d\phi} dr \nonumber\]

en el lado derecho de la ecuación, acabamos de cambiar el orden de integración para tener el\(dr\) último, y codificamos por colores la expresión para que podamos identificarnos fácilmente\(p(r)\) como:

\[\label{eq:p(r)} p(r)=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}|\psi(r,\theta,\phi)|^2\;r^2 \sin\theta\; d\theta d\phi\]

La ecuación\ ref {eq:p (r)} es la formulación matemática de lo que queríamos: una función de densidad de probabilidad que no dependa de los ángulos. Nos integramos\(\phi\) y\(\theta\) así lo que nos queda representa la dependencia con\(r\).

Podemos multiplicar ambos lados por\(r\):

\[rp(r)=r\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}{\color{Red}|\psi(r,\theta,\phi)|^2}{\color{OliveGreen}r^2 \sin\theta\; d\theta d\phi}=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}{\color{Red}|\psi(r,\theta,\phi)|^2}r{\color{OliveGreen}r^2 \sin\theta\; d\theta d\phi} \nonumber\]

y usa la ecuación\ ref {eq:mean_r} para calcular\(\left \langle r \right \rangle\)

\[\label{eq:coordinates12} \left \langle r \right \rangle = \int\limits_{0}^{\infty}{\color{Magenta}p(r) r} \;dr=\int\limits_{0}^{\infty}{\color{Magenta}\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}|\psi(r,\theta,\phi)|^2r\;r^2 \sin\theta\; d\theta d\phi}dr\]

Los colores en estas expresiones están dirigidos a ayudarte a rastrear de dónde provienen los diferentes términos.

Veamos más de cerca la ecuación\ ref {eq:coordinates12}. Básicamente, acabamos de concluir que:

\[\label{eq:coordinates13} \left \langle r \right \rangle = \int\limits_{all\;space}|\psi|^2r\;dV\]

donde\(dV\) es el diferencial de volumen en coordenadas esféricas. Sabemos que\(\psi\) está normalizado, entonces

\[\int\limits_{all\;space}|\psi|^2\;dV=1 \nonumber\]

Si multiplicamos el integrando por\(r\), obtenemos\(\left \langle r \right \rangle\). Discutiremos una extensión de esta idea cuando hablemos de operadores. Por ahora, usemos la Ecuación\ ref {eq:coordinates13} para calcular\(\left \langle r \right \rangle\) para el orbital 1s.

Ejemplo\(\PageIndex{1}\)

Calcular el valor promedio de\(r\),\(\left \langle r \right \rangle\), para un electrón en el orbital 1s del átomo de hidrógeno. La función de onda normalizada de la órbita 1s, expresada en coordenadas esféricas, es:

\[\psi_{1s}=\dfrac{1}{\sqrt{\pi a_0^3}}e^{-r/a_0} \nonumber\]

Solución

El valor promedio de\(r\) es:

\[\left \langle r \right \rangle=\int\limits_{0}^{\infty}p(r)r\;dr \nonumber\]

o

\[\left \langle r \right \rangle = \int\limits_{all\;space}|\psi|^2r\;dV \nonumber\]

La diferencia entre la primera expresión y la segunda expresión es que en el primer caso, ya integramos sobre los ángulos\(\theta\) y\(\phi\). La segunda expresión es una triple integral porque\(|\psi|^2\) aún conserva la información angular.

No tenemos\(p(r)\), así que o lo obtenemos primero de\(|\psi|^2\), o directamente utilizamos\(|\psi|^2\) y realizamos la triple integración:

\[\left \langle r \right \rangle = \int\limits_{0}^{\infty}\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}|\psi(r,\theta,\phi)|^2r\;{\color{Red}r^2 \sin\theta\; d\theta d\phi dr} \nonumber\]

La expresión resaltada en rojo es el diferencial de volumen.

Para este orbital,

\[|\psi(r,\theta,\phi)|^2=\dfrac{1}{\pi a_0^3}e^{-2r/a_0} \nonumber\]

y luego,

\[\left \langle r \right \rangle = \dfrac{1}{\pi a_0^3}\int\limits_{0}^{\infty}e^{-2r/a_0}r^3\;dr\int\limits_{0}^{2\pi}d\phi\int\limits_{0}^{\pi}\sin\theta\; d\theta=\dfrac{4}{a_0^3}\int\limits_{0}^{\infty}e^{-2r/a_0}r^3\;dr \nonumber\]

De la hoja de fórmulas:

\(\int_{0}^{\infty}x^ne^{-ax}dx=\dfrac{n!}{a^{n+1}},\; a>0, n\)es un entero positivo.

Aquí,\(n=3\) y\(a= 2/a_0\).

\[\dfrac{4}{a_0^3}\int\limits_{0}^{\infty}r^3e^{-2r/a_0}\;dr=\dfrac{4}{a_0^3}\times \dfrac{3!}{(2/a_0)^4}=\dfrac{3}{2}a_0 \nonumber\]

\[\displaystyle{\color{Maroon}\left \langle r \right \rangle=\dfrac{3}{2}a_0} \nonumber\]

De Ejemplo\(\PageIndex{1}\), notamos que en promedio esperamos ver el electrón a una distancia del núcleo igual a 1.5 veces\(a_0\). Esto quiere decir que si pudieras medir\(r\), y realizas esta medición en un gran número de átomos de hidrógeno, o en el mismo átomo muchas veces, verías, en promedio, el electrón a una distancia del núcleo\(r=1.5 a_0\). Sin embargo, la probabilidad de ver el electrón es mayor en\(r=a_0\) (página). Vemos que el promedio de una distribución no necesariamente necesita igualar el valor al que la probabilidad es más alta ².