15.7: Valores propios y vectores propios

Dado que las matrices cuadradas son operadores, no debería sorprenderte que podamos determinar sus valores propios y vectores propios. Los vectores propios son análogos a las funciones propias que discutimos en el Capítulo 11.

Si\(\mathbf{A}\) es una\(n\times n\) matriz, entonces un vector distinto de cero\(\mathbf{x}\) se llama un vector propio de\(\mathbf{A}\) if\(\mathbf{Ax}\) es un múltiplo escalar de\(\mathbf{x}\):

\[\mathbf{A}\mathbf{x}=\lambda \mathbf{x}\]

El escalar\(\lambda\) se llama el valor propio de\(\mathbf{A}\), y\(\mathbf{x}\) se dice que es un vector propio. Por ejemplo, el vector\((2,0)\) es un vector propio de

\[\mathbf{A}=\begin{pmatrix} -2&0 \\ 0&1 \end{pmatrix} \nonumber\]

con valor propio\(\lambda=-2\):

\[\begin{pmatrix} -2&0 \\ 0&1 \end{pmatrix}\begin{pmatrix} 2\\ 0 \end{pmatrix}=-2\begin{pmatrix} 2\\ 0 \end{pmatrix} \nonumber\]

Observe que la matriz\(\mathbf{A}\), como cualquier otra\(2\times 2\) matriz, transforma un vector bidimensional en otro que en general se encontrará en una dirección diferente. Por ejemplo, si tomamos\((2,2)\), esta matriz la transformará en\(\mathbf{A}(2,2)=(-4,2)\), que tiene una orientación diferente. Sin embargo, el vector\((2,0)\) es especial, porque esta matriz lo transforma en un vector que es un múltiplo de sí mismo:\(\mathbf{A}(2,0)=(-4,0)\). Para este vector en particular, ¡la matriz se comporta como un número! (en este caso el número -2). De hecho, tenemos toda una familia de vectores que hacen lo mismo:\(\mathbf{A}(x,0)=(-4x,0)\), o en otras palabras, cualquier vector paralelo al\(x-\) eje. Hay otra familia de vectores que hace que\(\mathbf{A}\) se comporten como un número:\(\mathbf{A}(0,y)=(0,y)\), o en otras palabras, cualquier vector paralelo al\(y-\) eje hace que\(\mathbf{A}\) se comporte como el número 1.

El argumento anterior da una interpretación geométrica a vectores propios y valores propios. Para una\(2\times 2\) matriz, hay dos líneas 'especiales' en el plano. Si tomamos un vector a lo largo de una de estas líneas, la matriz se comporta como un número que llamamos el valor propio, y simplemente encoge o expande el vector sin cambiar su dirección.

Ejemplo\(\PageIndex{1}\)

Los vectores\(\mathbf{x}_1=(-i,1)\) y\(\mathbf{x}_2=(i,1)\) son los dos vectores propios de

\[\mathbf{A}=\begin{pmatrix} 1&1 \\ -1&1 \end{pmatrix} \nonumber\]

¿Cuáles son los valores propios correspondientes?

Solución

Por definición:

\[\begin{pmatrix} 1&1 \\ -1&1 \end{pmatrix}\begin{pmatrix} -i\\ 1 \end{pmatrix}=\lambda_1\begin{pmatrix} -i\\ 1 \end{pmatrix}\nonumber\]

donde\(\lambda_1\) está el vector propio correspondiente a\(\mathbf{x}_1\)

Contamos con:

\[\begin{pmatrix} 1&1 \\ -1&1 \end{pmatrix}\begin{pmatrix} -i\\ 1 \end{pmatrix}=\begin{pmatrix} -i+1\\ i+1 \end{pmatrix}=(1+i)\begin{pmatrix} -i\\ 1 \end{pmatrix}\nonumber\]

y por lo tanto\(\lambda_1=(1+i)\).

Para el segundo vector propio:

\[\begin{pmatrix} 1&1 \\ -1&1 \end{pmatrix}\begin{pmatrix} i\\ 1 \end{pmatrix}=\lambda_2\begin{pmatrix} i\\ 1 \end{pmatrix}\nonumber\]

donde\(\lambda_2\) está el vector propio correspondiente a\(\mathbf{x}_2\)

Contamos con:

\[\begin{pmatrix} 1&1 \\ -1&1 \end{pmatrix}\begin{pmatrix} i\\ 1 \end{pmatrix}=\begin{pmatrix} i+1\\ -i+1 \end{pmatrix}=(1-i)\begin{pmatrix} i\\ 1 \end{pmatrix}\nonumber\]

y por lo tanto\(\lambda_2=(1-i)\).

La pregunta obvia ahora es cómo encontrar los valores propios de una matriz. Nos concentraremos en\(2\times 2\) las matrices, aunque por supuesto existen métodos para hacer lo mismo en dimensiones superiores.

Digamos que queremos encontrar los vectores propios de

\[\mathbf{A}=\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\nonumber\]

Los vectores propios satisfacen la siguiente ecuación:

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\lambda\begin{pmatrix} x \\ y \end{pmatrix}\nonumber\]

Nuestro primer paso será multiplicar el lado derecho por la matriz de identidad. Esto es análogo a multiplicar por el número 1, por lo que no hace nada:

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\lambda\begin{pmatrix} 1&0 \\ 0&1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \nonumber\]

Ahora vamos a agrupar todos los términos del lado izquierdo:

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}-\lambda\begin{pmatrix} 1&0 \\ 0&1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=0 \nonumber\]

distribuir\(\lambda\):

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}-\begin{pmatrix} \lambda&0 \\ 0&\lambda \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=0 \nonumber\]

y agrupar las dos matrices en una:

\[\begin{pmatrix} 3-\lambda&2 \\ -1&0-\lambda \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=0 \nonumber\]

multiplicando la matriz por el vector:

\[(3-\lambda)x+2y=0 \nonumber\]

\[-x-\lambda y=0 \nonumber\]

que da:

\[ \begin{align*} (3-\lambda)(-\lambda y)+2y &=0 \\[4pt] y[(3-\lambda)(-\lambda )+2] &=0 \end{align*} \nonumber\]

No queremos forzar\(y\) a ser cero, porque estamos tratando de determinar el vector propio, que puede tener\(y\neq 0\). Entonces, concluimos que

\[[(3-\lambda)(-\lambda )+2]=0 \label{characteristic equation}\]

que es una ecuación cuadrática en\(\lambda\). Ahora bien, tenga en cuenta que\([(3-\lambda)(-\lambda )+2]\) es el determinante

\[\begin{vmatrix} 3-\lambda&2 \\ -1&-\lambda \end{vmatrix} \nonumber\]

Acabamos de concluir que para resolver

\[\begin{pmatrix} 3-\lambda&2 \\ -1&0-\lambda \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=0 \nonumber\]

solo tenemos que mirar los valores de\(\lambda\) que hacen que el determinante de la matriz sea igual a cero:

\[\begin{vmatrix} 3-\lambda&2 \\ -1&-\lambda \end{vmatrix}=0 \nonumber\]

La ecuación\ ref {ecuación característica} se llama la ecuación característica de la matriz, y en el futuro podemos saltarnos algunos pasos y escribirla directamente.

Empecemos el problema desde cero. Digamos que queremos encontrar los vectores propios de

\[\mathbf{A}=\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix} \nonumber\]

Solo necesitamos restar\(\lambda\) de la diagonal principal, y establecer el determinante de la matriz resultante en cero:

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\rightarrow\begin{pmatrix} 3-\lambda&2 \\ -1&0-\lambda \end{pmatrix}\rightarrow \begin{vmatrix} 3-\lambda&2 \\ -1&-\lambda \end{vmatrix}=0 \nonumber\]

Obtenemos una ecuación cuadrática en\(\lambda\):

\[\begin{vmatrix} 3-\lambda&2 \\ -1&-\lambda \end{vmatrix}=(3-\lambda)(-\lambda)+2=0 \nonumber\]

que se pueden resolver para obtener los dos valores propios:\(\lambda_1=1\) y\(\lambda_2=2\).

Nuestro siguiente paso es obtener los vectores propios correspondientes, que satisfagan:

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}=1\begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \nonumber\]

para\(\lambda_1\)

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=2\begin{pmatrix} x_2 \\ y_2 \end{pmatrix} \nonumber\]

para\(\lambda_2\)

Resolvamos ambos lado a lado:

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}=1\begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \nonumber\] \[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}=1\begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \nonumber\] \[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}-1\begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}=0 \nonumber\] \[\begin{pmatrix} 3-1&2 \\ -1&0-1 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}=0 \nonumber\] \[\begin{pmatrix} 2&2 \\ -1&-1 \end{pmatrix}\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}=0 \nonumber\] \[2x_1+2y_1=0 \nonumber\] \[-x_1-y_1=0 \nonumber\] Observe que estas dos ecuaciones no son independientes, ya que la parte superior es un múltiplo de la inferior. Ambos dan el mismo resultado:\(y=-x\). Esto significa que cualquier vector que se encuentre en la línea\(y=-x\) es un vector propio de esta matriz con valor propio\(\lambda=1\).

\[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=2\begin{pmatrix} x_2 \\ y_2 \end{pmatrix} \nonumber\] \[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=2\begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix} \nonumber\] \[\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}-2\begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=0 \nonumber\] \[\begin{pmatrix} 3-2&2 \\ -1&0-2 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=0 \nonumber\] \[\begin{pmatrix} 1&2 \\ -1&-2 \end{pmatrix}\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=0 \nonumber\] \[x_2+2y_2=0 \nonumber\] \[-x_2-2y_2=0 \nonumber\] Observe que estas dos ecuaciones no son independientes, ya que la parte superior es un múltiplo de la inferior. Ambos dan el mismo resultado:\(y=-x/2\). Esto significa que cualquier vector que se encuentre en la línea\(y=-x/2\) es un vector propio de esta matriz con valor propio\(\lambda=2\).

La figura\(\PageIndex{1}\) muestra las líneas\(y=-x\) y\(y=-x/2\). Cualquier vector que se encuentre a lo largo de la línea\(y=-x/2\) es un vector propio con valor propio\(\lambda=2\), y cualquier vector que se encuentre a lo largo de la línea\(y=-x\) es un vector propio con valor propio\(\lambda=1\). Los vectores propios que difieren solo en un factor constante no se tratan como distintos. Es conveniente y convencional normalizar los vectores propios. Observe que podemos calcular dos vectores propios normalizados para cada autovalor (apuntando en una u otra dirección), y la distinción entre uno u otro no es importante.

Figura\(\PageIndex{1}\): Los vectores propios de\(\mathbf{A}\) (CC BY-NC-SA; Marcia Levitus)

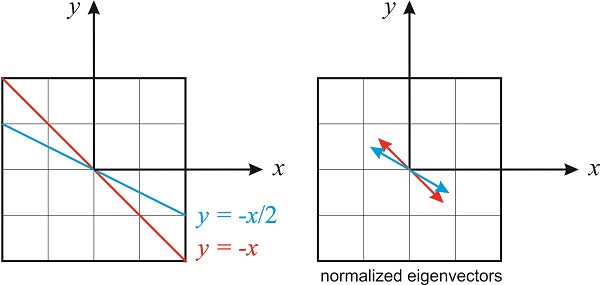
En el primer caso, tenemos\(y=-x\). Esto significa que cualquier vector de la forma\(\begin{pmatrix} a \\ -a \end{pmatrix}\) es un vector propio, pero estamos buscando el valor de\(a\) que haga que este autovector se normalice. En otras palabras, queremos\((a)^2+(-a)^2=1\), lo que da\(a=\pm 1/\sqrt{2}\). En conclusión, ambos

\[\begin{array}{c c c} \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \end{pmatrix} & \text{and} & \dfrac{1}{\sqrt{2}}\begin{pmatrix} -1 \\ 1 \end{pmatrix} \end{array} \nonumber\]

son vectores propios normalizados de

\[\mathbf{A}=\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix} \nonumber\]

con valor propio\(\lambda=1\).

Porque\(\lambda=2\), tenemos eso\(y=-x/2\). Esto significa que cualquier vector de la forma\(\begin{pmatrix} a \\ -a/2 \end{pmatrix}\) es un vector propio, pero estamos buscando el valor de\(a\) que haga que este autovector se normalice. En otras palabras, queremos\((a)^2+(-a/2)^2=1\), lo que da\(a=\pm 2/\sqrt{5}\). En conclusión, ambos

\[\begin{array}{c c c} \dfrac{1}{\sqrt{5}}\begin{pmatrix} 2 \\ -1 \end{pmatrix} & \text{and} & \dfrac{1}{\sqrt{5}}\begin{pmatrix} -2 \\ 1 \end{pmatrix} \end{array} \nonumber\]

son vectores propios normalizados de

\[\mathbf{A}=\begin{pmatrix} 3&2 \\ -1&0 \end{pmatrix} \nonumber\]

con valor propio\(\lambda=2.\)

Ejemplo\(\PageIndex{2}\)

Encuentra los valores propios y los vectores propios nomalizados de

\[\mathbf{M}=\begin{pmatrix} 0&1 \\ -1&0 \end{pmatrix} \nonumber\]

Los valores propios satisfacen la ecuación característica:

\[\begin{vmatrix} -\lambda&1 \\ -1&-\lambda \end{vmatrix}=0\rightarrow (-\lambda)(-\lambda)-(1)(-1)=\lambda^2+1=0\rightarrow \lambda_{1,2}=\pm i \nonumber\]

Para\(\lambda =i\):

\[\begin{pmatrix} 0&1 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_1\\ y_1 \end{pmatrix}=i\begin{pmatrix} x_1\\ y_1 \end{pmatrix} \nonumber\]

\[y_1=ix_1 \nonumber\]

\[-x_1=i y_1 \nonumber\]

Nuevamente, las dos ecuaciones que obtenemos tienen la misma información (o más formalmente, son linealmente dependientes). De cualquiera de los dos, obtenemos\(y_1=i x_1\).

Cualquier vector de la forma

\[\mathbf{u}=\begin{pmatrix} a\\ ia \end{pmatrix} \nonumber\]

es un vector propio de\(\mathbf{M}\) con valor propio\(\lambda=i\).

Para normalizar el vector (Sección 14.4), calculamos el módulo del vector usando el producto punto:

\[|\mathbf{u}|^2=\mathbf{u}^*\cdot\mathbf{u} \nonumber\]

(ver Sección 14.2 para una discusión sobre el producto punto de vectores complejos)

\[|\mathbf{u}|^2=\mathbf{u}^*\cdot\mathbf{u}=a^2+(ia)(-ia)=a^2+a^2=2a^2\rightarrow |\mathbf{u}|=\pm\sqrt{2}a \nonumber\]

y dividimos el vector por su módulo.

Los vectores propios normalizados para\(\lambda =i\) son, por lo tanto,

\[\hat{\mathbf{u}}=\pm \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1\\ i \end{pmatrix} \nonumber\]

Para\(\lambda =-i\):

\[\begin{pmatrix} 0&1 \\ -1&0 \end{pmatrix}\begin{pmatrix} x_1\\ y_1 \end{pmatrix}=-i\begin{pmatrix} x_1\\ y_1 \end{pmatrix} \nonumber\]

\[y_1=-ix_1 \nonumber\]

\[-x_1=-i y_1 \nonumber\]

De cualquiera de los dos, obtenemos

\[y_1=-i x_1. \nonumber\]

Cualquier vector de la forma

\[\mathbf{v}=\begin{pmatrix} a\\ -ia \end{pmatrix} \nonumber\]

es un vector propio de\(\mathbf{M}\) con valor propio\(\lambda=-i\).

Para normalizar el vector, calculamos el producto punto:

\[|\mathbf{v}|^2=\mathbf{v}^*\cdot\mathbf{v}=a^2+(-ia)(ia)=a^2+a^2=2a^2\rightarrow |\mathbf{v}| =\pm\sqrt{2}a \nonumber\]

Los vectores propios normalizados para\(\lambda =-i\) son, por lo tanto,

\[\hat{\mathbf{v}}=\pm \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1\\ -i \end{pmatrix} \nonumber\]

Valores propios de la matriz: algunas propiedades importantes

1) Los valores propios de una matriz triangular son los elementos diagonales.

\[\begin{pmatrix} a&b&c\\ 0&d&e\\ 0&0&f \end{pmatrix}\rightarrow \lambda_1=a;\;\lambda_2=d;\;\lambda_3=f \nonumber\]

2) Si\(\lambda_1\),\(\lambda_2\)... ,\(\lambda_n\), son los valores propios de la matriz\(\mathbf{A}\), entonces\(|\mathbf{A}|= \lambda_1\lambda_2...\lambda_n\)

3) La traza de la matriz\(\mathbf{A}\) es igual a la suma de todos los valores propios de la matriz\(\mathbf{A}\).

Por ejemplo, para la matriz

\[\mathbf{A}=\begin{pmatrix} 1&1\\ -2&4 \end{pmatrix}\rightarrow |\mathbf{A}|=6=\lambda_1\lambda_2;\;Tr(\mathbf{A})=5=\lambda_1+\lambda_2 \nonumber\]

Para una\(2\times 2\) matriz, la traza y el determinante son información suficiente para obtener los valores propios:\(\lambda_1=2\) y\(\lambda_2=3\).

4) Las matrices simétricas-aquellas que tienen un “plano espejo” a lo largo de la diagonal norte-suroeste (es decir\(\mathbf{A}=\mathbf{A}^T\)) deben tener todos los valores propios reales. Sus vectores propios son mutuamente ortogonales.

Por ejemplo, para la matriz

\[\mathbf{A}=\begin{pmatrix} -2&4&0\\ 4&1&-1\\ 0&-1&-3 \end{pmatrix} \nonumber\]

los tres autovalores son\(\lambda_1=1+\sqrt{21}\)\(\lambda_2=1-\sqrt{21}\),\(\lambda_3=-2\), y los tres vectores propios:

\[ \begin{array}{c} \mathbf{u}_1=\begin{pmatrix} -5-\sqrt{21}\\ -4-\sqrt{21}\\ 1 \end{pmatrix}, & \mathbf{u}_2=\begin{pmatrix} -5+\sqrt{21}\\ -4+\sqrt{21}\\ 1 \end{pmatrix}, & \text{and} & \mathbf{u}_3=\begin{pmatrix} 1\\ -1\\ 1 \end{pmatrix} \end{array} \nonumber\]

Puede probar que los vectores propios son mutuamente ortogonales tomando sus productos de punto.