1.24: Vibraciones moleculares

El movimiento vibracional en las moléculas diatómicas a menudo se discute dentro del contexto del oscilador armónico simple en la mecánica cuántica. Una molécula diatómica tiene sólo un enlace sencillo que puede vibrar; decimos que tiene un solo modo vibracional. Como es de esperar, los movimientos vibracionales de las moléculas poliatómicas son mucho más complicados que los de una diatómica. En primer lugar, hay más enlaces que pueden vibrar; y en segundo lugar, además de estirar las vibraciones, el único tipo de vibración posible en un diatómico, también podemos tener modos vibratorios de flexión y torsión. Dado que cambiar la longitud de un enlace en un poliatómico a menudo afectará la longitud de los enlaces cercanos, no podemos considerar el movimiento vibratorio de cada enlace de forma aislada; en cambio, hablamos de modos normales que involucran el movimiento concertado de grupos de enlaces. Como ejemplo sencillo, a continuación se muestran los modos normales de una molécula triatómica lineal.

Una vez que conocemos la simetría de una molécula en su estructura de equilibrio, la teoría de grupos nos permite predecir los movimientos vibracionales que sufrirá utilizando exactamente las mismas herramientas que usamos anteriormente para investigar orbitales moleculares. Cada modo vibracional se transforma como una de las representaciones irreducibles del grupo puntual de la molécula. Antes de pasar a un ejemplo, revisaremos rápidamente cómo determinar el número de modos vibratorios en una molécula.

Grados moleculares de libertad — determinando el número de modos vibratorios normales

Un átomo puede sufrir solo movimiento de traslación, y por lo tanto tiene tres grados de libertad correspondientes al movimiento a lo largo del\(x\), \(y\), and \(z\) Cartesian axes. Translational motion in any arbitrary direction can always be expressed in terms of components along these three axes. When atoms combine to form molecules, each atom still has three degrees of freedom, so the molecule as a whole has \(3N\) degrees of freedom, where \(N\) is the number of atoms in the molecule. However, the fact that each atom in a molecule is bonded to one or more neighboring atoms severely hinders its translational motion, and also ties its motion to that of the atoms to which it is attached. For these reasons, while it is entirely possible to describe molecular motions in terms of the translational motions of individual atoms (we will come back to this in the next section), we are often more interested in the motions of the molecule as a whole. These may be divided into three types: translational; rotational and vibrational.

Al igual que para un átomo individual, la molécula en su conjunto tiene tres grados de libertad traslacional, dejando\(3N - 3\) degrees of freedom in rotation and vibration.

El número de grados de libertad rotacional depende de la estructura de la molécula. En general, existen tres posibles grados de libertad rotacional, correspondientes a la rotación alrededor del\(x\), \(y\), and \(z\) Cartesian axes. A non-linear polyatomic molecule does indeed have three rotational degrees of freedom, leaving \(3N - 6\) degrees of freedom in vibration (i.e \(3N - 6\) vibrational modes). In a linear molecule, the situation is a little different. It is generally accepted that to be classified as a true rotation, a motion must change the position of one or more of the atoms. If we define the \(z\) axis as the molecular axis, we see that spinning the molecule about the axis does not move any of the atoms from their original position, so this motion is not truly a rotation. Consequently, a linear molecule has only two degrees of rotational freedom, corresponding to rotations about the \(x\) and \(y\) axis. This type of molecule has \(3N - 5\) degrees of freedom left for vibration, or \(3N - 5\) vibrational modes.

En resumen:

• Una molécula lineal tiene\(3N - 5\) vibrational modes
• Una molécula no lineal tiene\(3N - 6\) vibrational modes.

Determinación de las simetrías de los movimientos moleculares

Se mencionó anteriormente que el procedimiento para determinar los modos vibratorios normales de una molécula poliatómica es muy similar al utilizado en secciones anteriores para construir orbitales moleculares. De hecho, prácticamente la única diferencia entre estas dos aplicaciones de la teoría de grupos es la elección del conjunto de bases.

Como ya hemos establecido, los movimientos de una molécula pueden describirse en términos de los movimientos de cada átomo a lo largo del\(x\), \(y\) and \(z\) axis. Consequently, it probably won’t come as too much of a surprise to discover that a very useful basis for describing molecular motions comprises a set of \(\begin{pmatrix} x, y, z \end{pmatrix}\) axes centered on each atom. This basis is usually known as the \(\textit{3N}\) Cartesian basis (since there are \(3N\) Cartesian axes, \(3\) axes for each of the \(N\) atoms in the molecule). Note that each molecule will have a different \(3N\) Cartesian basis, just as every molecule has a different atomic orbital basis.

Nuestra primera tarea en la investigación de movimientos de una molécula en particular es determinar los caracteres de los representantes de la matriz para\(3N\) Cartesian basis under each of the symmetry operations in the molecular point group. We will use the \(H_2O\) molecule, which has \(C_{2v}\) symmetry, as an example.

\(H_2O\) has three atoms, so the \(3N\) Cartesian basis will have \(9\) elements. The basis vectors are shown in the diagram below.

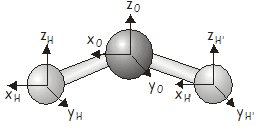
Una forma de determinar los personajes sería construir todos los representantes de la matriz y tomar sus huellas. Si bien eres más que bienvenido a probar este enfoque si quieres algo de práctica en la construcción de representantes matriciales, hay una manera más fácil. Recordemos que también podemos determinar el carácter de una matriz representativa bajo una operación de simetría particular, pasando por las funciones base y aplicando las siguientes reglas:

1. Agregar\(1\) al carácter si la función base no cambia por la operación de simetría;
2. Agregar\(-1\) al carácter si la función de base cambia signo bajo la operación de simetría;
3. Agregue\(0\) al carácter si la función base se mueve cuando se aplica la operación de simetría.

Para\(H_2O\), this gives us the following characters for the \(3N\) Cartesian basis (check that you can obtain this result using the rules above and the basis vectors as drawn in the figure):

\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 9 & -1 & 3 & 1 \end{array} \tag{24.1}\]

Hay una manera aún más rápida de resolver los personajes del\(3N\) Cartesian basis if you have a character table in front of you. The character for the Cartesian basis is simply the sum of the characters for the \(x\), \(y\), and \(z\) (or \(T_x\), \(T_y\), and \(T_z\)) functions listed in the character table. To get the character for the \(\textit{3N}\) Cartesian basis, simply multiply this by the number of atoms in the molecule that are unshifted by the symmetry operation.

El\(C_{2v}\) character table is shown below.

\[\begin{array}{l|cccc|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & h = 4 \\ \hline A_1 & 1 & 1 & 1 & 1 & z, x^2, y^2, z^2 \\ A_2 & 1 & 1 & -1 & -1 & xy, R_z \\ B_1 & 1 & -1 & 1 & -1 & x, xz, R_y \\ B_2 & 1 & -1 & -1 & 1 & y, yz, R_x \\ \hline \end{array} \tag{24.2}\]

\(x\) transforms as \(B_1\), \(y\) as \(B_2\), and \(z\) as \(A_1\), so the characters for the Cartesian basis are

\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 3 & -1 & 1 & 1 \end{array} \tag{24.3}\]

Multiplicamos cada uno de estos por el número de átomos no desplazados (\(3\) for the identity operation, \(1\) for \(C_2\), \(3\) for \(\sigma_v\) y\(1\) for \(\sigma_v'\)) para obtener los caracteres para el\(3N\) Cartesian basis.

\[\begin{array}{lcccc} \chi_{3N}: & 9 & -1 & 3 & 1 \end{array} \tag{24.4}\]

De manera tranquilizadora, obtenemos los mismos personajes que antes. Cuál de los tres métodos que utilice para llegar a este punto depende de usted.

Ahora tenemos los caracteres para los movimientos moleculares (descritos por el\(3N\) Cartesian basis) under each symmetry operation. At this point, we want to separate these characters into contributions from translation, rotation, and vibration. This turns out to be a very straightforward task. We can read the characters for the translational and rotational modes directly from the character table, and we obtain the characters for the vibrations simply by subtracting these from the \(3N\) Cartesian characters we’ve just determined. The characters for the translations are the same as those for \(\chi_{Cart}\). Encontramos los personajes para las rotaciones sumando los personajes para\(R_x\), \(R_y\), and \(R_z\) from the character table (or just \(R_x\) and \(R_y\) if the molecule is linear). For \(H_2O\), we have:

\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 9 & -1 & 3 & 1 \\ \chi_{\text{Trans}}: & 3 & -1 & 1 & 1 \\ \chi_{\text{Rot}}: & 3 & -1 & -1 & -1 \\ \chi_{\text{Vib}} = \chi_{3N} - \chi_{\text{Trans}} - \chi_{\text{Rot}}: & 3 & 1 & 3 & 1 \end{array} \tag{24.5}\]

Los personajes de la fila final son las sumas de los personajes para todas las vibraciones moleculares. Podemos conocer las simetrías de las vibraciones individuales utilizando la ecuación de reducción (Ecuación (15.20)) para determinar la contribución de cada representación irreducible.

En muchos casos ni siquiera necesitarás usar la ecuación, y puedes averiguar qué representaciones irreducibles están contribuyendo con solo inspeccionar la tabla de caracteres. En el presente caso, la única combinación de representaciones irreducibles que pueden dar los valores requeridos para\(\chi_{\text{Vib}}\) es\(2A_1 + B_1\). As an exercise, you should make sure you are also able to obtain this result using the reduction equation.

Hasta ahora todo esto puede parecer un poco abstracto, y probablemente quieras saber es cuáles son las vibraciones de\(H_2O\) actually look like. For a molecule with only three atoms, it is fairly easy to identify the possible vibrational modes and to assign them to the appropriate irreducible representation.

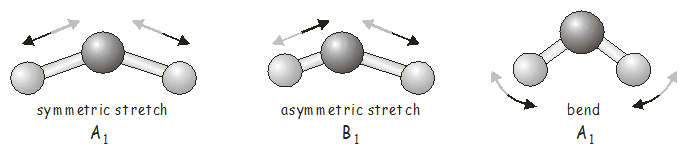
Para una molécula más grande, el problema puede llegar a ser mucho más complejo, y en ese caso podemos generar las SALC del\(3N\) Cartesian basis, which will tell us the atomic displacements associated with each vibrational mode. We will do this now for \(H_2O\).

Desplazamientos atómicos usando la base cartesiana 3N

Como antes, generamos las SALC de cada simetría aplicando el operador de proyección apropiado a cada una de las funciones base (o en este caso, vectores base)\(f_i\) in turn.

\[\phi_i = \sum_g \chi_k(g) g f_i \tag{24.6}\]

En este caso tenemos\(9\) basis vectors, which we will label \(x_H\), \(y_H\), \(z_H\), \(x_O\), \(y_O\), \(z_O\), \(x_{H'}\), \(y_{H'}\), \(z_{H'}\), describing the displacements of the two \(H\) atoms and the \(O\) atom along Cartesian axes. For the SALCs of \(A_1\) symmetry, applying the projection operator to each basis vector in turn gives (check that you can obtain this result):

\[\begin{array}{rclll} \phi_1(x_H) & = & x_H - x_{H'} + x_H - x_{H'} & = & 2x_H - 2x_{H'} \\ \phi_2(y_H) & = & y_H - y_{H'} - y_H + y_{H'} & = & 0 \\ \phi_3(z_H) & = & z_H + z_{H'} + z_H + z_{H'} & = & 2z_H + 2z_{H'} \\ \phi_4(x_O) & = & x_O - x_O + x_O - x_O & = & 0 \\ \phi_5(y_O) & = & y_O - y_O - y_O + y_O & = & 0 \\ \phi_6(z_O) & = & z_O + z_O + z_O + z_O & = & 4z_O \\ \phi_7(x_{H'}) & = & x_{H'} - x_H + x_{H'} - x_H & = & 2x_{H'} - 2x_H \\ \phi_8(y_{H'}) & = & y_{H'} - y_H - y_{H'} + y_H & = & 0 \\ \phi_9(z_{H'}) & = & z_{H'} + z_H + z_{H'} + z_H & = & 2z_{H'} + 2z_H \end{array} \tag{24.7}\]

Vemos que el movimiento característico de un\(A_1\) vibration (which we have identified as the symmetric stretch and the bending vibration) may be summarized as follows:

1. \(2(x_H - x_{H'})\)- los dos átomos de hidrógeno se mueven en direcciones opuestas a lo largo del\(x\) eje.
2. \(2(z_H + z_{H'})\)- los dos átomos de hidrógeno se mueven en la misma dirección a lo largo del\(z\) eje.
3. \(4z_O\)- el átomo de oxígeno se mueve a lo largo del\(z\) eje.
4. No hay movimiento de ninguno de los átomos en la\(y\) dirección.

El estiramiento asimétrico tiene\(B_1\) symmetry, and applying the projection operator in this case gives:

\[\begin{array}{rclll} \phi_1(x_H) & = & x_H + x_{H'} + x_H + x_{H'} & = & 2x_H + 2x_{H'} \\ \phi_2(y_H) & = & y_H + y_{H'} - y_H - y_{H'} & = & 0 \\ \phi_3(z_H) & = & z_H - z_{H'} + z_H - z_{H'} & = & 2z_H - 2z_{H'} \\ \phi_4(x_O) & = & x_O + x_O + x_O + x_O & = & 4x_O \\ \phi_5(y_O) & = & y_O + y_O - y_O - y_O & = & 0 \\ \phi_6(z_O) & = & z_O - z_O + z_O - z_O & = & 0 \\ \phi_7(x_{H'}) & = & x_{H'} + x_H + x_{H'} + x_H & = & 2x_{H'} + 2x_H \\ \phi_8(y_{H'}) & = & y_{H'} + y_H - y_{H'} - y_H & = & 0 \\ \phi_(z_{H'}) & = & z_{H'} - z_H + z_{H'} - z_H & = & 2z_{H'} - 2z_H \end{array} \tag{24.8}\]

En este modo vibracional, los dos\(H\) atoms move in the same direction along the \(x\) axis and in opposite directions along the \(z\) axis.

Ahora hemos demostrado cómo se puede utilizar la teoría de grupos junto con el\(3N\) Cartesian basis to identify the symmetries of the translational, rotational and vibrational modes of motion of a molecule, and also to determine the atomic displacements associated with each vibrational mode.

Vibraciones moleculares usando coordenadas internas

Si bien fue bastante sencillo investigar los desplazamientos atómicos asociados con cada modo vibratorio de\(H_2O\) using the \(3N\) Cartesian basis, this procedure becomes more complicated for larger molecules. Also, we are often more interested in how bond lengths and angles change in a vibration, rather than in the Cartesian displacements of the individual atoms. If we are only interested in looking at molecular vibrations, we can use a different procedure from that described above, and start from a basis of internal coordinates. Internal coordinates are simply a set of bond lengths and bond angles, which we can use as a basis for generating representations and, eventually, SALCs. Since bond lengths and angles do not change during translational or rotational motion, no information will be obtained on these types of motion.

Para\(H_2O\), the three internal coordinates of interest are the two \(OH\) bond lengths, which we will label \(r\) and \(r'\), and the \(HOH\) bond angle, which we will label \(\theta\) . Si quisiéramos, podríamos separar nuestra base en dos bases diferentes, una que consiste solo en longitudes de unión, para describir las vibraciones de estiramiento, y otra que consiste solo en ángulos de unión, para describir las vibraciones de flexión. Sin embargo, el ejemplo actual es lo suficientemente simple como para tratar todas las funciones básicas juntas.

Como es habitual, nuestro primer paso es elaborar los caracteres de los representantes matriciales para esta base bajo cada operación de simetría. Los efectos de las diversas transformaciones sobre nuestra base elegida, y los personajes de los representantes correspondientes, son:

\[\begin{array}{lc} E(r, r', \theta) = (r, r', \theta) & \chi(E) = 3 \\ C_2(r, r', \theta) = (r', r, \theta) & \chi(C_2) = 1 \\ \sigma_v(xz)(r, r', \theta) = (r, r', \theta) & \chi(\sigma_v) = 3 \\ \sigma_v'(yz)(r, r', \theta) = (r', r, \theta) & \chi(\sigma_v') = 1 \end{array} \tag{24.9}\]

Estos son los mismos caracteres que encontramos antes de usar el\(3N\) Cartesian basis, and as before, we can see by inspection of the character table that the representation may be reduced down to the sum of irreducible representations \(2A_1 + B_1\). We can now work out the symmetry adapted linear combinations of our new basis set to see how the bond lengths and angle change as \(H_2O\) vibrates in each of the three vibrational modes.

Nuevamente, utilizaremos el operador de proyección\(\phi_i = \Sigma_g \chi_k(g) g f_i\) aplicado a cada función base por turno.

En primer lugar, el\(A_1\) vibrations:

\[\begin{array}{rclll} \phi_1(r) & = & r + r' + r + r' & = & 2(r + r') \\ \phi_2(r') & = & r' + r + r' + r & = & 2(r' + r) \\ \phi_3(\theta) & = & \theta + \theta + \theta + \theta & = & 4\theta \end{array} \tag{24.10}\]

A partir de estas SALC, podemos identificar\(\phi_1\) (y\(\phi_2\), que es idéntico) con el estiramiento simétrico, en el que ambas longitudes de enlace cambian de fase entre sí, y\(\phi_3\) con la curva.

Ahora para el\(B_1\) vibration:

\[\begin{array}{rclll} \phi_4(r) & = & r - r' + r - r' & = & 2(r - r') \\ \phi_5(r') & = & r' - r + r' - r & = & 2(r' - r) \\ \phi_6(\theta) & = & \theta - \theta + \theta - \theta & = & 0 \end{array} \tag{24.11}\]

\(\phi_4\) and \(\phi_5\)no son linealmente independientes, y cualquiera puede elegirse para describir el estiramiento asimétrico, en el que un enlace se alarga a medida que el otro se acorta.

Nota: Cuando se utilizan coordenadas internas, es importante que todas las coordenadas en la base sean linealmente independientes. Si este es el caso entonces el número de coordenadas internas en la base será el mismo que el número de modos vibracionales (\(3N - 5\) or \(3N - 6\), depending on whether the molecule is linear or non-linear). This requirement is satisfied in the \(H_2O\) example above. For a less straightforward example, consider the methane molecule, \(CH_4\). It might appear that we could choose a basis made up of the four \(C\)-\(H\) bond lengths and the six \(H\)-\(C\)-\(H\) bond angles. However, this would give us \(10\) basis functions, and \(CH_4\) has only \(9\) vibrational modes. This is due to the fact that the bond angles are not all independent of each other. It can be tricky to come up with the appropriate internal coordinate basis to describe all of the molecular motions, but all is not lost. Even if you can’t work out the appropriate bond angles to choose, you can always take a basis of bond lengths to investigate the stretching vibrations of a molecule. If you want to know the symmetries of the bending vibrations, you can use the \(3N\) Cartesian basis method to determine the symmetries of all of the vibrational modes and compare these with the stretching mode symmetries to identify the bending modes.

Colaboradores y Atribuciones

Claire Vallance (University of Oxford)