Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

9.8: Equilibrios ácido-base

Última actualización

30 oct 2022
Guardar como PDF
- 9.7: El método de bulbo Dumas para medir el equilibrio de descomposición
- 9.9: Búferes

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Muchos procesos implican transferencia de protones, o tipos de reacciones ácido-base. Como muchos sistemas biológicos dependen del pH cuidadosamente controlado, este tipo de procesos son extremadamente importantes. El pH se define por

$pH \equiv -\log a(\ce{H^{+}}) \approx -\log [\ce{H^{+}}] \label{eq1}$

donde $a$ es la actividad de los iones hidronio y $[\ce{H^{+}}]$ es la verdadera concentración de iones hidronio (ambos en mol/L).

La disociación de un ácido débil en el agua se rige por el equilibrio definido por

$HA(aq) \rightleftharpoons H^+(aq) + A^-(aq)$

La constante de equilibrio para tal reacción, $K_a$ , toma la forma

$K_a = \dfrac{[H^+][A^-]}{[HA]} \label{eq3}$

Como es el caso de todas las constantes de equilibrio termodinámico, las concentraciones son reemplazadas por actividades y la constante de equilibrio es sin unidades. Sin embargo, si todas las especies se comportan idealmente (tienen coeficientes de actividad unitaria) las unidades pueden ser utilizadas como una guía muy útil en la resolución de problemas.

Ejemplo $\PageIndex{1}$ : Acetic Acid

¿Cuál es el pH de una solución de HOAc (ácido acético) 0.200 M? (K _a = 1.8 x 10 ^-5 M)

Solución:

¡Una mesa ICE vendrá muy útil aquí!

	$[HOAc]$	$[H^+]$	$[OAc^-]$
I nitial	\ ([HOAc]\) ">0.200 M	\ ([H^+]\) ">0	\ ([OAC^-]\) ">0
C hange	\ ([HOAc]\) ">-x	\ ([H^+]\) ">+x	\ ([OAC^-]\) ">+x
E quilibrium	\ ([HOAc]\) ">0.200 M - x	\ ([H^+]\) ">x	\ ([OAC^-]\) ">x

El problema del equilibrio puede entonces establecerse como

$K_a = \dfrac{[H^+][OAc^-]}{[HOAc]}$

Sustituyendo los valores que se conocen

$1.8 \times 10^{-5} =\dfrac{ x^2}{0.200 \, M -x}$

Esto produce una ecuación cuadrática, y así dos valores de los $x$ cuales satisfacen la relación.

$x_1 = -0.001906 \,M$

$x_2 = 0.001888 \,M$

La raíz negativa no es físicamente significativa ya que las concentraciones de $H^+$ y $OAc^-$ no pueden ser negativas. Usando el valor de $x_2$ as $[H^+]$ , entonces se calcula el pH (a través de la Ecuación\ ref {eq1}) para ser

$pH \approx -\log_{10} (0.001888) = 2.72$

La Auto-ionización del Agua

El agua es un solvente muy importante ya que las moléculas de agua tienen grandes momentos dipolares que crean interacciones favorables con compuestos iónicos. El agua también tiene una gran constante dieléctrica que ampara el campo eléctrico generado por los iones en las soluciones, haciendo que las interacciones comparativas con el agua sean más favorables que con otros iones en solución en muchos casos. Pero el agua también se disocia en iones a través de la reacción

$H_2O(l) \rightleftharpoons H^+(aq) + OH^-(aq) \label{eqA}$

La constante de equilibrio que rige esta disociación es altamente dependiente de la temperatura. Los siguientes datos son presentados por Bandura y Lvov (Bandura & Lvov, 2006)

T (°C)	0	25	50	75	100
pK _w	14.95	13.99	13.26	12.70	12.25

A partir de estos datos, se puede construir una parcela de van 't Hoff.

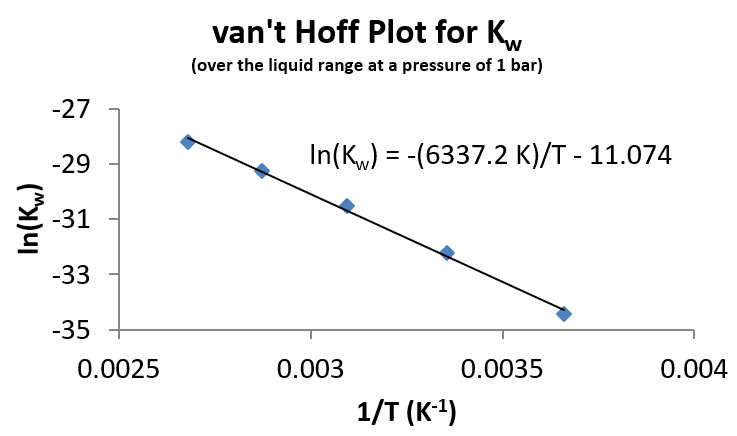
Figura $\PageIndex{1}$ : parcela van 't Hoff para la autoionización del agua.

Hay cierta curvatura en la línea, lo que sugiere cierta dependencia (aunque pequeña) de la temperatura $\Delta H_{rxn}$ para la Ecuación\ ref {eQa}. Sin embargo, a partir del ajuste de estos datos, se $\Delta H_{rxn}$ puede determinar que un valor de es de 52.7 kJ/mol. De particular interés es que la disociación es endotérmica, por lo que los aumentos de temperatura conducirán a un mayor grado de disociación.

Ejemplo $\PageIndex{2}$ : Neutral Water

¿Cuál es el pH del agua neutra a 37 °C (temperatura normal del cuerpo humano)? Agua neutra sin $[H^+]$ exceso de exceso $[OH^-]$ o viceversa.

Solución:

A partir de la línea de mejor ajuste en la gráfica van 't Hoff de la Figura $\PageIndex{1}$ , se $K_w$ puede calcular el valor de:

$\ln (K_w) = - \dfrac{6338 \,K}{310\,K} - 11.04$

$K_w= 2.12 \times 10^{-14}\,M^2$

Dado que $K_w$ da el producto de $[H^+]$ y $[OH^-]$ (que debe ser igual en una solución neutra),

$H^+] = \sqrt{2.12 \times 10^{-14}\,M^2} = 1.456 \times 10^{-7}\,M$

Y el pH viene dado por (Ecuación\ ref {eq1}):

$pH = -\log_{10} (1.456 \times 10^{-7}) = 6.84$

Nota: Esto es ligeramente inferior a un pH de 7.00, que normalmente se considera “neutro”. ¡Pero un pH de 7.00 solo es neutro a 25 °C! A temperaturas más altas, el pH neutro es un valor menor debido a la naturaleza endotérmica del agua de autoionización. Si bien tiene una $[H^+]$ concentración más nigher, también tiene una mayor $[OH^-]$ y al mismo nivel, por lo que sigue siendo técnicamente neutral.

La hidrólisis de una base débil

La hidrólisis se define como una reacción con agua que divide una molécula de agua. La hidrólisis de una base débil define la constante de equilibrio K _b.

$A^- + H_2O \rightleftharpoons HA + OH^-$

Para esta reacción, la constante de equilibrio $K_b$ viene dada por

$K_b = \dfrac{[HA][OH^-]}{[A^-]}$

La concentración (o actividad) del compuesto puro H ₂ O no se incluye en la expresión de equilibrio porque, al ser un compuesto puro en su estado estándar, tiene actividad unitaria a lo largo del proceso de establecimiento del equilibrio. Además, cabe señalar que cuando K _b se combina con la expresión para _Ka para el ácido débil HA (Ecuación\ ref {eq3}),

$K_a K_b = \left( \dfrac{[H^+][A^-]}{[HA]} \right) \left( \dfrac{[HA][OH^-]}{[A^-]} \right) = [H^+][OH^-] = K_w$

Como consecuencia, si se sabe $K_a$ por un ácido débil, también se sabe $K_b$ por su base conjugada, ya que el producto resulta en $K_w$ .

Ejemplo $\PageIndex{3}$ :

¿Cuál es el pH de una solución 0.150 M de KF? (Para HF, pK _a = 3.17 a 25 °C)

Solución:

El problema implica la hidrólisis de la base conjugada de HF, F ^-. La reacción de hidrólisis es

$F^- + H_2O \rightleftharpoons HF + OH^-$

Aquí está en orden una mesa ICE.

	$F^-$	$HF$	$OH^-$
I nitial	\ (F^-\) ">0.150 M	\ (HF\) ">0	\ (OH^-\) ">0
C hange	\ (F^-\) ">-x	\ (HF\) ">+x	\ (OH^-\) ">+x
E quilibrium	\ (F^-\) ">0.150 M - x	\ (HF\) ">x	\ (OH^-\) ">x

Entonces la expresión para $K_b$ es

$K_b = \dfrac{K_w}{K_a} = \dfrac{1.0 \times 10^{-14} M^2}{10^{3.17} M} = \dfrac{x^2}{1.50 \,M-x}$

En este caso, el pequeño valor de $K_b$ asegura que el valor de x será insignificantemente pequeño en comparación con 0.150 M. En este límite, el valor de $x$ (que es igual a [OH ^-])

$x = [OH^-] = 1.49 \times 10^{-6}\,M$

Así $[H^+]$ es dado por

$[H^+] =\dfrac{K_w}{[OH^-]} = \dfrac{10^{-14} M^2}{1.49 \times 10^{-6} M} = 6.71 \times 10^{-9} \,M$

Y el pH viene dado por (Ecuación\ ref {eq1}):

$pH = -\log_{10} (6.71 \times 10^{-9}) = 8.17$

Nota: El pH de esta solución salina es ligeramente básico. Esto es de esperar ya que se puede pensar que KF se forma en la reacción de un ácido débil (HF) con una base fuerte (KOH). En la competencia por controlar el pH, la base fuerte termina ganando la batalla.

La Auto-ionización del Agua

La hidrólisis de una base débil

Support Center

How can we help?