3.5: Se cuantifica la energía de una partícula en una caja
- Page ID
- 79975
- Resolver el modelo de partícula en caja utilizado para describir una partícula atrapada en un pozo 1 D
- Caracterizar los estados propios de partículas en una caja (es decir, las funciones de onda) y las energías propias en función del número cuántico
- Demostrar que los autoestados son ortogonales
El sistema de modelo de partículas en caja es la aplicación no trivial más simple de la ecuación de Schrödinger, pero que ilustra muchos de los conceptos fundamentales de la mecánica cuántica. Para una partícula que se mueve en una dimensión (nuevamente a lo largo del eje x), se puede escribir la ecuación de Schrödinger
\[-\dfrac{\hbar^2}{2m}\psi {}''(x)+ V (x)\psi (x) = E \psi (x) \nonumber \]
Supongamos que la partícula puede moverse libremente entre dos puntos finales\(x = 0\) y\(x = L\), pero no puede penetrar más allá de ninguno de los extremos. Esto es equivalente a una energía potencial dependiente de\(x\) con
\ [V (x) =\ comenzar {casos}
0 & 0\ leq x\ leq L\
\ infty & x< 0\; and\; x> L\ fin {casos}\ nonumber\]
Este potencial se representa en la Figura 3.5.1 . La energía potencial infinita constituye una barrera impenetrable ya que la partícula tendría una energía potencial infinita si se encontrara ahí, lo cual es claramente imposible.
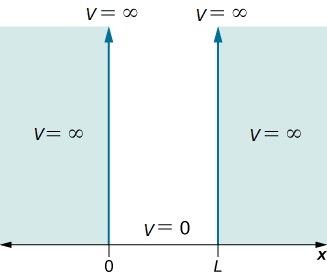
La partícula se une así a un “pozo potencial" ya que la partícula no puede penetrar más allá\(x = 0\) o\(x = L\)
\[\psi (x)=0\; \; \; for \; \; x<0\; \; and\; \; x>L\label{3.5.3} \]
Por el requisito de que la función de onda sea continua, debe ser cierto también que
\[\psi (0)=0\; \; \; and\; \; \; \psi (L)=0\label{3.5.4} \]
que constituye un par de condiciones de límite en la función de onda dentro de la caja. Dentro de la caja,\(V(x) = 0\), por lo que la ecuación de Schrödinger se reduce a la forma de partículas libres:
\[-\dfrac{\hbar^2}{2m}\psi{}''(x)=E\psi (x) \label{3.5.5} \]
con\( 0\leq x\leq L\).
Nuevamente tenemos la ecuación diferencial
\[\psi {}''(x) +k^2\psi (x)=0 \label{3.5.6} \]
con
\[k^2 = \dfrac{2mE}{\hbar^2} \label{3.5.6a} \]
La solución general se puede escribir
\[\psi (x)=A\: \sin\; kx\,+\, B\: \cos\; kx\label{3.5.7} \]
donde\(A\) y\(B\) son constantes a determinar por las condiciones de contorno en la Ecuación\(\ref{3.5.4}\). Por la primera condición, encontramos
\[\psi (0)=A\, \sin\, 0\, +\, B\, \cos\, 0\, =\, B\,= 0\label{3.5.8} \]
La segunda condición límite en\(x = L\) ese momento implica
\[\psi (a)=A\, \sin\, kL\,=\, 0\label{3.5.9} \]
Se supone que\(A \neq 0\), pues de lo contrario\(\psi(x)\) sería cero en todas partes y la partícula desaparecería (es decir, la solución trivial). La condición que\(\sin kx = 0\) implica que
\[kL\, =\, n\pi \label{3.5.10} \]
donde\(n\) es un entero, positivo, negativo o cero. El caso\(n = 0\) debe ser excluido, pues entonces\(k = 0\) y otra vez\(\psi(x)\) desaparecería en todas partes. Eliminando\(k\) entre Ecuación\(\ref{3.5.6}\) y\(\ref{3.5.10}\), obtenemos
\[E_{n}=\dfrac{\hbar^2\pi^2}{2mL^2}\, n^2=\dfrac{h^2}{8mL^2}n^2 \label{3.5.11} \]
con\(n=1,2,,3...\).
Estos son los únicos valores de la energía que permiten soluciones de la Ecuación de Schrödinger\(\ref{3.5.5}\) consistentes con las condiciones límite en la Ecuación\(\ref{3.5.4}\). El número entero\(n\), llamado número cuántico, se agrega como subíndice\(E\) para etiquetar los niveles de energía permitidos. Los valores negativos de\(n\) añadir nada nuevo porque las energías en Ecuación\(\ref{3.5.11}\) dependen de\(n^2\).
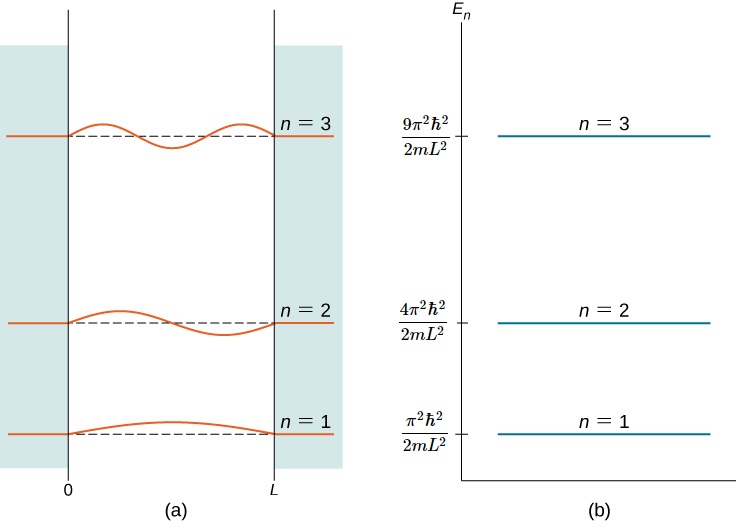
La figura 3.5.2 muestra parte del diagrama de nivel de energía para la partícula en una caja. La ocurrencia de niveles de energía discretos o cuantificados es característica de un sistema unido, es decir, uno confinado a una región finita en el espacio. Para la partícula libre, la ausencia de confinamiento permitió un continuo energético. Tenga en cuenta que, en ambos casos, el número de niveles de energía es infinito-denumerablemente infinito para la partícula en una caja, pero no denumerablemente infinito para la partícula libre.
La partícula en una caja asume su menor energía posible cuando\(n = 1\), a saber
\[E_{1}=\dfrac{h^2}{8mL^2}\label{3.5.12} \]
El estado de menor energía para un sistema cuántico se denomina estado fundamental.
Un punto interesante es que\(E_{1} > 0\), mientras que el sistema clásico correspondiente tendría una energía mínima de cero. Se trata de un fenómeno recurrente en la mecánica cuántica. La energía residual del estado fundamental, es decir, la energía superior al mínimo clásico, se conoce como energía de punto cero. En efecto, la energía cinética, de ahí el impulso, de una partícula unida no puede reducirse a cero. El valor mínimo de impulso se encuentra equiparando\(E_{1}\) a\(p^2/2m\), dando\(p_{min}\) =\(\pm h/2L\). Esto se puede expresar como una incertidumbre en el impulso dado por\(\Delta p\approx h/L\). Acoplando esto con la incertidumbre en la posición\(\Delta x\approx L\),, desde el tamaño de la caja, podemos escribir
\[\Delta x\Delta p\approx h\label{3.5.13} \]
Esto está de acuerdo con el principio de incertidumbre de Heisenberg.
Las funciones propias de partículas en una caja están dadas por la Ecuación\(\ref{3.5.14}\), con\(B = 0\) y\(k = n\pi/L=a\), de acuerdo con la Ecuación\(\ref{3.5.10}\)
\[\psi _{n}(x)=A\, \sin\dfrac{n\pi x}{L} \label{3.5.14} \]
con\(n=1,2,3...\).
Estas, al igual que las energías, pueden ser etiquetadas por el número cuántico\(n\). La constante\(A\), hasta ahora arbitraria, se puede ajustar para que\(\psi _{n}(x)\) se normalice. La condición de normalización es, en este caso,
\[\int_{0}^{a}\begin{bmatrix}\psi_{n}(x) \end{bmatrix}^2\,dx=1\label{3.5.15} \]
la integración que se ejecuta sobre el dominio de la partícula\(0\leq x\leq L\). Sustituyendo la ecuación\(\ref{3.5.14}\) en ecuación\(\ref{3.5.15}\),
\[\begin{align} A^2\: \int_{0}^{L}\, \sin^2\, \dfrac{n\pi x}{L}dx &=A^2\dfrac{L}{n\pi}\int_{0}^{n\pi}\sin^2\, \theta \,d\theta \\[4pt] &=A^2\dfrac{L}{2}=1\label{3.5.16} \end{align} \]
Hemos hecho la sustitución\(\theta=n\pi x/L\) y utilizado el hecho de que el valor promedio de\(\sin^2 \theta\) más de un número integral de medias longitudes de onda es igual a 1/2 (alternativamente, uno podría referirse a tablas integrales estándar). A partir de la ecuación\(\ref{3.5.16}\), podemos identificar la constante de normalización general
\[A = \sqrt{ \dfrac{2}{L}} \nonumber \]
para todos los valores de\(n\). Finalmente podemos escribir las funciones propias normalizadas:
\[\psi _{n}(x)=\sqrt{\dfrac{2}{L}} \sin \dfrac{n\pi x}{L} \label{3.5.17} \]
con\(n=1,2,3...\).
Las primeras funciones propias y las distribuciones de probabilidad correspondientes se trazan en la Figura 3.5.3 . Existe una estrecha analogía entre los estados de este sistema cuántico y los modos de vibración de una cuerda de violín. Los patrones de ondas estacionarias en la cuerda son, de hecho, idénticos en forma a las funciones de onda en la ecuación\(\ref{3.5.17}\).
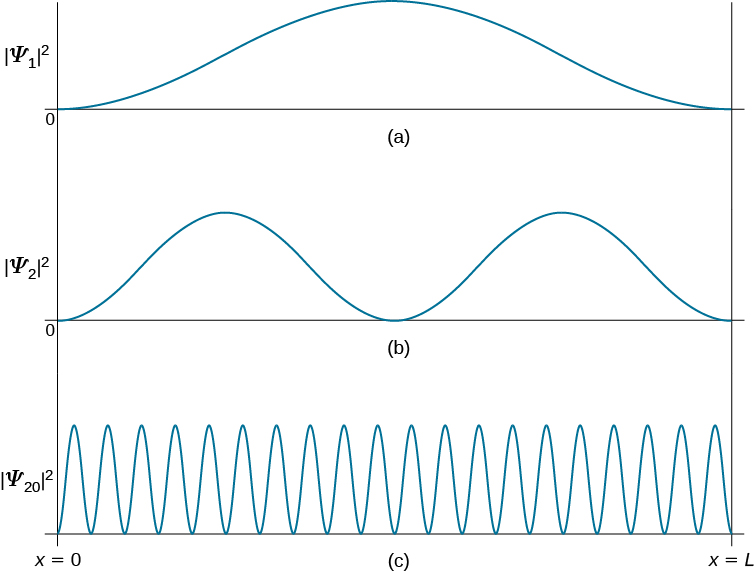
Una característica significativa de los estados cuánticos de partículas en una caja es la ocurrencia de nodos. Se trata de puntos, distintos de los dos puntos finales (que están fijados por las condiciones de contorno), en los que la función de onda desaparece. En un nodo hay exactamente cero probabilidad de encontrar la partícula. El n-ésimo estado cuántico tiene, de hecho,\(n-1\) nodos. En general es cierto que el número de nodos aumenta con la energía del estado cuántico, lo cual puede ser racionalizado por el siguiente argumento cualitativo. A medida que aumenta el número de nodos, también lo hace el número y la pendiente de los 'meneo' en la función de onda. Es como esquiar por un curso de slalom. En consecuencia, la curvatura promedio, dada por la segunda derivada, debe aumentar. Pero la segunda derivada es proporcional al operador de energía cinética. Por lo tanto, cuantos más nodos, mayor será la energía. Esto demostrará ser una guía invaluable en sistemas cuánticos más complejos.
Para una partícula en una caja unidimensional de longitud\(L\), el segundo estado excitado wavefunction (\(n=3\)) es
\[\psi_3=\sqrt{\dfrac{2}{L}}\sin{\dfrac{3\pi x}{L}} \nonumber \]
- ¿Cuál es la probabilidad de que la partícula esté en la mitad izquierda de la caja?
- ¿Cuál es la probabilidad de que la partícula esté en el tercio medio de la caja?
Solución
Probabilidad de que la partícula se encuentre entre\(a\) y\(b\) es
\[P(a,b)=\int^b_a \psi^2\,dx \nonumber \]
Para este problema,
\[\psi_3=\sqrt{\dfrac{2}{L}}\sin{\dfrac{3\pi x}{L}} \nonumber \]
por lo tanto,
\[ \begin{align*} P(a,b) &=\dfrac{2}{L} \int^b_a \sin^2 {\dfrac{3\pi x}{L}}\,dx \\ &=\left.\dfrac{2}{L}\left(\dfrac{x}{2}-\dfrac{L\sin \left( \dfrac{6\pi x}{L}\right)}{12\pi} \right) \right|^b_a \\[4pt] &=\dfrac{b-a}{L}-\dfrac{1}{6\pi} \left[ \sin \left(\dfrac{6\pi b}{L}\right) - \sin \left( \dfrac{6\pi a}{L} \right) \right] \end{align*} \nonumber \]
(a) La probabilidad de que la partícula esté en la mitad izquierda de la caja es
\[ \begin{align*} P\left(0,\dfrac{L}{2}\right) &=\dfrac{\dfrac{L}{2}-0}{L}-\dfrac{1}{6\pi}\left[ \sin \left( \dfrac{6\pi \left(\dfrac{L}{2}\right)}{L}\right) - \sin \left( \dfrac{6\pi (0)}{L}\right) \right] \\[4pt] &= \dfrac{1}{2} \end{align*} \nonumber \]
b) La probabilidad de que la partícula esté en el tercio medio de la caja
\[ \begin{align*} P\left(\dfrac{L}{3},\dfrac{2L}{3}\right) &=\dfrac{\dfrac{2L}{3}-\dfrac{L}{3}}{L}-\dfrac{1}{6\pi}\left[{\sin {\dfrac{6\pi \left(\dfrac{2L}{3}\right)}{L} }-\sin {\dfrac{6\pi \left(\dfrac{L}{3}\right) }{L} }}\right] \\[4pt] &=\dfrac{1}{3} \end{align*} \nonumber \]
Para una partícula en una caja unidimensional, la función de onda del estado fundamental es
\[\psi_1 = \sqrt{\dfrac{2}{L}} \sin\dfrac{x\pi}{L} \nonumber \]
¿Cuál es la probabilidad de que la partícula esté en la mitad izquierda de la caja en el estado fundamental?
- Contestar
-
\[ \begin{align} P\left(0,\frac{L}{2}\right) &= \dfrac{2}{L} \int^{\frac{L}{2}}_0 \sin^2 \dfrac{x\pi}{L} dx \nonumber\\ &=\dfrac{2}{L} \dfrac{\dfrac{L\pi}{L}+\sin 0+\sin \dfrac{L\pi}{L}}{\dfrac{4\pi}{L}} \nonumber\\ &=\dfrac{1}{2} \nonumber \end{align} \nonumber \]
Esta es la misma respuesta que para el\(\psi_3\) estado en Ejemplo 3.5.1 . Esto se debe a que el autoestado al cuadrado (.e., densidad de probabilidad) para la partícula en una caja 1D siempre será simétrico alrededor del centro de la caja. Por lo que habrá igual probabilidad de estar a ambos lados (es decir, no se favorece a ningún lado).
Recordemos que la dependencia del tiempo de la función de onda con potencial independiente del tiempo se discutió en la Sección 3.1 y se expresa como
\[\Psi(x,t)=\psi(x)e^{-iEt / \hbar} \nonumber \]
así que para la partícula en una caja, estos son
\[\psi _{n}(x)=\sqrt{\dfrac{2}{L}} \sin \dfrac{n\pi x}{L} e^{-iE_nt / \hbar} \label{PIBtime} \]
con\(E_n\) dada por la Ecuación\ ref {3.5.11}.
La parte de fase de la Ecuación\ ref {pibTime} se puede expandir en una parte real y en componentes complejos. Entonces la función de onda total para una partícula en una caja es
\[\Psi(x,t)= \underbrace{\left(\sqrt{\dfrac{2}{L}} \sin \dfrac{n\pi x}{L}\right) \left(\cos \dfrac{E_nt}{\hbar}\right)}_{\text{real part}} - \underbrace{i \left(\, \sqrt{\dfrac{2}{L}} \sin \dfrac{n\pi x}{L} \right) \left(\sin \dfrac{E_nt}{\hbar} \right) }_{\text{imaginary part}} \nonumber \]
que se puede simplificar (ligeramente) a
\[\Psi(x,t)= \underbrace{\left(\sqrt{\dfrac{2}{L}} \sin \dfrac{n\pi x}{L}\right) \left(\cos \dfrac{E_nt}{\hbar}\right)}_{\text{real part}} - \underbrace{i \left(\, \sqrt{\dfrac{2}{L}} \sin \dfrac{n\pi x}{L} \right) \left(\cos \dfrac{E_nt}{\hbar} - \dfrac{\pi}{2} \right) }_{\text{imaginary part}} \nonumber \]
Como se discutió anteriormente, la parte imaginaria de la función de onda total oscila fuera de fase\(π/2\) con respecto a la parte real (a esto lo llamamos “fuera de fase”). Esto se demuestra en el comportamiento dependiente del tiempo de las tres primeras funciones propias en la Figura 3.5.4 .
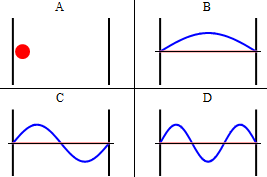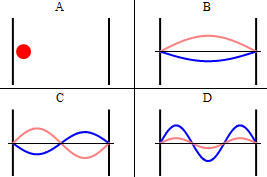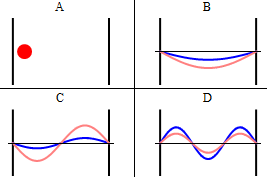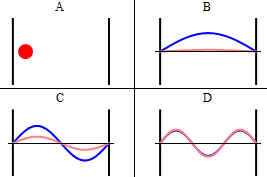
Tenga en cuenta que a medida que\(n\) aumenta, la energía de la función de onda aumenta (Ecuación\ ref {3.5.11}) y tanto el número de nodos como de antinodos aumentan y la frecuencia de oscilación de la función de onda aumenta.
Generalmente es cierto en sistemas cuánticos (no solo para partículas en cajas) que el número de nodos en una función de onda aumenta con la energía del estado cuántico.
Ortonormalidad de los autoestados
Otra propiedad importante de las funciones propias en Ecuación\(\ref{3.5.17}\) se aplica a la integral sobre un producto de dos funciones propias diferentes (Ecuación\ ref {3.5.17}). Es fácil ver en la Figura 3.5.5 que la integral
\[\int_{0}^{L}\psi _{2}(x)\psi _{1}(x)dx=0 \label{3.5.18} \]
La integral en la Ecuación\ ref {3.5.18} es cero cuando los dos estados de encendido difieren y cuando se integran en todo el rango del sistema (de\(-\infty\) a\(\infty\) para una partícula 1-D en la caja, pero esto puede ser una región estrecha de\(0\) a\(L\) ya que los autoestados son cero fuera de la caja).
Para probar la ecuación\ ref {3.5.18} para una partícula en un modelo de caja, podemos usar la identidad trigonométrica
\[\sin\,\alpha \: \sin\, \beta =\dfrac{1}{2}\begin{bmatrix}\cos(\alpha -\beta )-\cos(\alpha +\beta )\end{bmatrix} \label{trig} \]
para demostrar que
\[\int_{0}^{L}\psi _{m}(x)\psi _{n}(x)dx=0\: \: \: if\: \: \: m \neq n\label{3.5.19} \]
Esta propiedad se llama ortogonalidad. Mostraremos en el siguiente capítulo, que este es un resultado general de las funciones propias cuántico-mecánicas. La normalización (Ecuación\(\ref{3.5.18}\)) junto con la ortogonalidad (Ecuación\(\ref{3.5.19}\)) se pueden combinar en una sola relación
\[\int_{0}^{L}\psi _{m}(x)\psi _{n}(x)dx=\delta _{mn}\label{3.5.20} \]
En términos del delta de Kronecker
\ [\ delta _ {mn} =\ comenzar {casos}
1 &\ texto {si}\,\, m=n\\ [4pt]
0 &\ texto {si}\,\, m\ neq n\ fin {casos}\ etiqueta {3.5.21}\]
Un conjunto de funciones\(\begin{Bmatrix}\psi_{n}\end{Bmatrix}\) que obedece a la Ecuación\(\ref{3.5.20}\) se llama ortonormal.
Evaluar
- \(\langle \psi_3| \psi_3 \rangle \)
- \(\langle \psi_4| \psi_4 \rangle \)
- \(\langle \psi_3| \psi_4 \rangle \)
- \(\langle \psi_4| \psi_3 \rangle \)
para las funciones de onda normalizadas:
\[|\psi_3 \rangle = \sqrt{ \dfrac{2}{L}} \sin\dfrac{3\pi x}{L} \nonumber \]
y
\[|\psi_4 \rangle = \sqrt{ \dfrac{2}{L}} \sin\dfrac{4\pi x}{L}\nonumber \]
Estrategia
Se trata de cuatro integrales diferentes y podemos resolverlas directamente o usar ortonormalidad (Ecuación\ ref {3.5.21}) para evaluar.
a.
\[ \begin{align*} \langle \psi_3| \psi_3 \rangle &= \int_{-\infty}^{+\infty} \left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{3\pi x}{L} \right)\left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{3\pi x}{L} \right)\, dx \\[4pt] &= \dfrac{2}{L} \int_{-\infty}^{+\infty} \sin^2 \dfrac{3\pi x}{L} \, dx \end{align*} \nonumber \]
Esta es una integración sobre una función par, por lo que no se puede tirar a través de la simetría. Podemos usar la relación Trigonometría en Ecuación\ ref {trig} para obtener
\[ \dfrac{2}{L} \int_{-\infty}^{+\infty} \sin^2 \dfrac{3\pi x}{L} \, dx = \dfrac{2}{L} \int_{-\infty}^{+\infty} \dfrac{1}{2} \left(1 - \cos \dfrac{6\pi x}{L}\right) \, dx \nonumber \]
y podemos continuar la diversión. Sin embargo, no hay necesidad. Dado que el podemos reconocer que\(\langle \psi_3| \psi_3 \rangle \) es 1 por los criterios de normalización el cual se pliega en los criterios ortonormales (Ecuación\ ref {3.5.21}).
Por lo tanto\(\langle \psi_3| \psi_3 \rangle = 1\).
b.
\[ \begin{align*} \langle \psi_4| \psi_4 \rangle &= \int_{-\infty}^{+\infty} \left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{4\pi x}{L} \right)\left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{4\pi x}{L} \right)\, dx \\[4pt] &= \dfrac{2}{L} \int_{-\infty}^{+\infty} \sin^2 \dfrac{4\pi x}{L} \, dx \end{align*} \nonumber \]
Podemos expandirnos y resolver, pero nuevamente no hay necesidad. Por lo tanto, las funciones de onda se normalizan\(\langle \psi_4| \psi_4 \rangle = 1\).
c.
\[ \begin{align*} \langle \psi_3| \psi_4 \rangle &= \int_{-\infty}^{+\infty} \left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{3\pi x}{L} \right)\left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{4\pi x}{L} \right)\, dx \\[4pt] &= \dfrac{2}{L} \int_{-\infty}^{+\infty} \sin \left( \dfrac{3\pi x}{L} \right) \sin \left( \dfrac{4\pi x}{L} \right)\, dx \end{align*} \nonumber \]
Podemos expandir esta integral y evaluar, pero como el integrando es impar (y la función par por un impar), esta integral es cero. Alternativamente, podemos usar los criterios de ortogonalidad en los criterios ortonormales mayores (Ecuación\ ref {3.5.21}).
d.
\[ \begin{align*} \langle \psi_4| \psi_3 \rangle &= \int_{-\infty}^{+\infty} \left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{4\pi x}{L} \right)\left( \sqrt{ \dfrac{2}{L}} \sin\dfrac{3\pi x}{L} \right)\, dx \\[4pt] &= \dfrac{2}{L} \int_{-\infty}^{+\infty} \sin \left(\dfrac{4\pi x}{L} \right) \sin \left( \dfrac{3\pi x}{L} \right)\, dx \end{align*} \nonumber \]
Podemos expandir esta integral y evaluar, pero como el integrando es impar (y la función par por una función impar), esta integral es cero. Alternativamente, podemos usar los criterios de ortogonalidad en los criterios ortonormales mayores (Ecuación\ ref {3.5.21}).
Sin embargo, dado que las funciones de onda son reales, entonces
\[\langle \psi_4| \psi_3 \rangle = \langle \psi_3| \psi_4 \rangle \nonumber \]
lo que también significa
\[\langle \psi_4| \psi_3 \rangle = 0 \nonumber \]
de los resultados de la sección c.
Colaboradores y Atribuciones
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)

