7.2: Interacciones intermoleculares
- Page ID
- 70770
- Nombra cinco tipos de unidades moleculares por las que puede estar compuesta la materia condensada.
- Dibuje una curva de energía potencial, mostrando claramente la separación de equilibrio y el mínimo de energía potencial.
- Declarar la diferencia entre atracciones consolidadas y no consolidadas.
- Explicar el significado y significado del momento dipolar de una molécula.
- Definir dipolo inducido y polarizabilidad.
- Declarar los seis tipos de fuerzas de atracción intermoleculares y sus fuerzas relativas.
Los líquidos y sólidos difieren de los gases en que se mantienen unidos por fuerzas que actúan entre las unidades moleculares individuales de las que están compuestos. En esta lección veremos más de cerca estas fuerzas para que puedas entender más fácilmente, y en muchos casos predecir, las diversas propiedades físicas de los muchos tipos de sólidos y líquidos que encontramos en el mundo.
La existencia misma de estados condensados de materia sugiere que existen fuerzas atractivas que actúan entre las unidades moleculares básicas de sólidos y líquidos. El término unidad molecular se refiere a la unidad estructural discreta más pequeña que compone el líquido o sólido. En la mayoría de los más de 15 millones de sustancias químicas que se conocen actualmente, estas unidades estructurales son moléculas reales, es decir, agregados de átomos que tienen sus propias propiedades distintivas, fórmulas y pesos moleculares. Pero las unidades moleculares también pueden ser átomos individuales, iones y unidades más extendidas. Como ocurre con la mayoría de las clasificaciones artificiales, estas distinciones tienden a descomponerse en casos extremos: la mayoría de los polímeros artificiales (“plásticos”) están compuestos por moléculas de varios tamaños y formas, algunas aleaciones metálicas contienen unidades moleculares identificables, y no es demasiado estiramiento considerar un diamante o un cristal de NaCl como una “molécula” en sí misma.
Curvas de Energía Potencial
A escala atómica o molecular, todas las partículas ejercen fuerzas atractivas y repulsivas entre sí. Si las fuerzas de atracción entre dos o más átomos son lo suficientemente fuertes como para convertirlos en una unidad perdurable con sus propias propiedades observables, llamamos al resultado una “molécula” y nos referimos a la fuerza como un “enlace químico”.
Las dos moléculas diatómicas representadas en la Figura\(\PageIndex{1}\) han entrado en estrecho contacto entre sí, pero la fuerza atractiva que actúa entre ellas no es lo suficientemente fuerte como para unirlas en una nueva unidad molecular, por lo que llamamos a esta fuerza una atracción no enlazante. A falta de estas atracciones no vinculantes, toda la materia existiría solo en estado gaseoso; no habría fases condensadas.
La distinción entre atracciones de enlace y no enlace se puede ver comparando la gráfica de energía potencial para un par de átomos de hidrógeno con la de dos átomos de argón (Figura\(\PageIndex{2}\)). A medida que se unen dos átomos de hidrógeno, la energía potencial cae al mínimo y luego se eleva rápidamente a medida que las dos nubes de electrones comienzan a repelerse entre sí. El mínimo de energía potencial define la energía y la longitud promedio del enlace H-H, dos de sus propiedades medibles únicas.
La energía potencial de un par de átomos de argón también cae a medida que se juntan, pero no lo suficiente como para sostenerlos juntos. (e.g., las leyes de la mecánica cuántica no permiten que este elemento de gas noble forme\(Ar_2\) moléculas estables). Sin embargo, estas atracciones sin unión permiten que el argón exista como líquido y sólido a bajas temperaturas, pero son incapaces de soportar las interrupciones causadas por la energía térmica a temperaturas ordinarias, por lo que comúnmente conocemos el argón como gas.
Efectos Térmicos
A partir de unas imágenes clásicas, a temperaturas superiores al cero absoluto, todas las partículas de escala molecular poseen energía térmica que las mantiene en constante movimiento (y a partir de una imagen cuántica, el movimiento no se detiene ni siquiera en cero absoluto debido al principio de Heisenberg Incertidumbre). La energía térmica promedio viene dada por el producto de la constante de gas R y la temperatura absoluta. A 25°C, esto funciona a
\[RT = (8.314 \,J \,K^{–1} mol^{–1}) (298\, K) = 2,480\, J\, mol^{–1} \approx 2.5\, kJ\, mol^{–1}\]
Un enlace químico funcional es mucho más fuerte que este (típicamente por encima de 100 kJ/mol), por lo que el efecto del movimiento térmico es simplemente hacer que el enlace vibre; solo a temperaturas más altas (donde el valor de RT es mayor) la mayoría de los enlaces comenzarán a romperse. Las fuerzas de atracción no enlazantes entre pares de átomos son generalmente demasiado débiles para sostener incluso una sola vibración. Además de propiedades distintivas únicas como energía de enlace, longitud de enlace y frecuencias de estiramiento, los enlaces covalentes suelen tener propiedades direccionales que dependen de las estructuras orbitales de los átomos componentes. Las atracciones no vinculantes mucho más débiles no poseen ninguna de estas propiedades.
La forma de una curva de energía potencial (a menudo aproximada como una curva “Morse”) muestra cómo las fuerzas repulsivas y atractivas afectan la energía potencial de maneras opuestas: las repulsiones siempre elevan esta energía, y las atracciones la reducen. La curva pasa por un mínimo cuando las fuerzas atractivas y repulsivas están exactamente en equilibrio. Como dijimos anteriormente, todas las partículas ejercen ambos tipos de fuerzas entre sí; estas fuerzas son todas básicamente de naturaleza eléctrica y se manifiestan de diversas maneras y con diferentes fortalezas.
La distancia correspondiente a la energía potencial mínima se conoce como distancia de equilibrio. Esta es la distancia promedio que mantendrán las dos partículas si no hay otras fuerzas que actúen sobre ellas, tal como podría surgir de la presencia de otras partículas cercanas. Una expresión empírica general para la curva de energía potencial de interacción entre dos partículas puede escribirse como
\[ E = Ar^{-n} + Br^{-m} \label{7.2.1}\]
\(A\)y\(B\) son constantes de proporcionalidad y\(n\) y\(m\) son números enteros. A esta expresión se le hace referencia a veces como la ecuación de Mie. El primer término,\(A\), corresponde a la repulsión es siempre positivo, y\(n\) debe ser mayor que\(m\), reflejando el hecho de que la repulsión siempre domina en pequeñas separaciones. El\(B\) coeficiente es negativo para las fuerzas de atracción, pero se volverá positivo para la repulsión electrostática entre cargas similares. Cuanto mayor sea el valor de uno de estos exponentes, más cerca deben acercarse las partículas antes de que la fuerza se vuelva significativa. La tabla\(\PageIndex{1}\) enumera los exponentes para los tipos de interacciones que describiremos en esta lección.
|
|
|
n |
|
|---|---|---|---|
| iones | Coulómbica | - | 1 |
| ion - molécula polar | ión-dipolo | - | 2 |
| dos moléculas polares | dipolo-dipolo | - | 3 |
| ion - molécula no polar | dipolo inducido por iones | - | 4 |
| molécula polar y no polar | dipolo - dipolo inducido | - | 6 |
| moléculas no polares | dispersión | - | 6 |
| repulsiones | cuántico | 9 | - |
| Nota: las interacciones de sombra azul se conocen colectivamente como interacciones de van der Waals | |||
La Fuerza Repulsiva Universal
El valor de\(n\) para la fuerza repulsiva en la Figura\(\PageIndex{3}\) es 9; esta puede ser la ley de potencia inversa más alta que se encuentra en la naturaleza. La magnitud de tal fuerza es insignificante hasta que las partículas están casi en contacto directo, pero una vez que entra en acción, se vuelve muy fuerte; si quieres tener una idea de ello, intenta golpearte la cabeza contra un muro de concreto. Porque la fuerza repulsiva es lo que impide que dos átomos ocupen el mismo espacio, esto es justo lo que esperarías. Si la fuerza repulsiva no siempre ganara contra todas las fuerzas atractivas, ¡toda la materia colapsaría en un enorme glob! La fuerza repulsiva universal surge directamente de dos aspectos principales de la teoría cuántica.
- Primero, el principio de incertidumbre de Heisenberg nos dice que los electrones situados dentro de los confines de un átomo poseen energía cinética que ejercería una presión externa si no fuera por la fuerza de atracción compensadora del núcleo cargado positivamente. Pero incluso la muy leve disminución de volumen que resultaría de apretar el átomo en un espacio más pequeño elevará esta presión para resistir efectivamente este cambio de volumen. Esta es la razón básica de que los estados condensados de la materia tienen compresibilidades extremadamente pequeñas.
- Trabajando de acuerdo con esto es el principio de exclusión de Pauli, cada electrón debe tener un conjunto diferente de números cuánticos. Entonces, a medida que dos partículas comienzan a entrometerse entre sí, el volumen que ocupan sus electrones se divide entre cada par de espinas, y las forzadas a estados cuánticos superiores normalmente ocuparían volúmenes aún mayores. El efecto es nuevamente elevar masivamente la energía potencial a medida que las partículas comienzan a exprimirse demasiado juntas.
En un maravilloso artículo (Science 187 605-612 1975), el físico Victor Weiskopf mostró cómo estas consideraciones, combinadas con algunas constantes fundamentales, conducen a estimaciones realistas de cosas como la dureza y compresibilidad de los sólidos, las alturas de las montañas, las longitudes de las olas del océano, y el tamaño de las estrellas.
Interacciones Ion-Ion
La atracción electrostática entre partículas cargadas eléctricamente es la más fuerte de todas las fuerzas intermoleculares. Estas fuerzas coulómbicas (como a menudo se les llama) provocan que atraigan cargas opuestas y como cargas para repeler.
Las fuerzas coulómbicas están involucradas en todas las formas de unión química; cuando actúan entre partículas cargadas separadas (interacciones ión-ion) son especialmente fuertes. Así, la energía requerida para separar un mol de iones Na + y Cl — en el cristal de cloruro de sodio es mayor que la necesaria para romper el enlace covalente en\(H_2\) (Figura\(\PageIndex{1}\)). Los efectos de la atracción ión-ion se ven más directamente en sólidos como el NaCl, que consisten en iones con carga opuesta dispuestos en dos redes cristalinas interpenetrantes.
Según la Ley de Coulomb la fuerza entre dos partículas cargadas viene dada por
\[ F= \dfrac{q_1q_2}{4\pi\epsilon_0 r^2} \label{7.2.2}\]
En lugar de usar unidades SI, los químicos suelen preferir expresar distancias a escala atómica en picometros y cargas como carga de electrones (±1, ±2, etc.) Usando estas unidades, la constante de proporcionalidad\(1/4\pi\epsilon\) funciona a\(2.31 \times 10^{16}\; J\; pm\). El signo de\(F\) determina si la fuerza será atractiva (—) o repulsiva (+); fíjese que este último es el caso siempre que las dos q tengan el mismo signo.
\(\ref{7.2.2}\)La ecuación es un ejemplo de una ley cuadrada inversa; la fuerza cae como el cuadrado de la distancia. Una ley similar rige la manera en que la iluminación se cae a medida que te alejas de una fuente de luz puntual; recuerda esto la próxima vez que te alejas de una luz de calle por la noche, y tendrás alguna sensación de lo que significa una ley cuadrada inversa.
Cuanto más fuerte es la fuerza de atracción que actúa entre dos partículas, mayor es la cantidad de trabajo requerido para separarlas. El trabajo representa un flujo de energía, por lo que la afirmación anterior es otra forma de decir que cuando dos partículas se mueven en respuesta a una fuerza, su energía potencial disminuye. Esta obra, como recordarás si has estudiado mecánica elemental, se encuentra integrando la fuerza negativa con respecto a la distancia sobre la distancia desplazada. Así, la energía que debe suministrarse para separar completamente dos partículas cargadas opuestamente inicialmente a una distancia r 0 viene dada por
\[ w= - \int _{r_o} ^{\infty} \dfrac{q_1q_2}{4\pi\epsilon_0 r}dr =- \dfrac{q_1q_2}{4\pi\epsilon_0 r_o} \label{7.2.3}\]
Cuando el cloruro de sodio se funde, algunos de los pares de iones se vaporizan y forman moléculas neutras de NaCl. ¿Cuánta energía se liberaría cuando un mol de iones Na + y Cl — se juntan de esta manera?
Solución
La energía liberada será la misma que la obra requerida para separar
\[ \begin{align*} E &= \dfrac{(2.31 \times 10^{16} J pm) (+1) (–1)}{276\; pm} \\[4pt] &= –8.37 \times 10^{–19}\; J \end{align*} \]
La interacción ión-ion es la más simple de las interacciones electrostáticas y existen otras interacciones de orden superior como se analiza a continuación.
Dipolos
Según la ley de Coulomb (Ecuación\(\ref{7.2.1}\)), la fuerza electrostática entre un ion y una partícula no cargada que tiene Q = 0 debe ser cero. Tenga en cuenta, sin embargo, que esta fórmula supone que las dos partículas son cargas puntuales que tienen radios cero. Una partícula real como un átomo o una molécula ocupa cierto volumen de espacio. Incluso si las cargas eléctricas de los protones y electrones se cancelan (como lo harán en cualquier átomo o molécula neutra), es posible que la distribución espacial de la nube de electrones que representa los electrones [valencia] más flojamente unidos pueda ser asimétrica, dando lugar a un momento dipolar eléctrico . Hay dos tipos de momentos dipolares:
- Los momentos dipolares eléctricos permanentes pueden surgir cuando se produce la unión entre elementos de diferentes electronegatividades.
- Los momentos dipolares inducidos (temporales) se crean cuando un campo eléctrico externo distorsiona la nube de electrones de una molécula neutra.
Un dipolo eléctrico se refiere a una separación de carga eléctrica. Un dipolo eléctrico idealizado consta de dos cargas puntuales de magnitud + q y — q separadas por una distancia r. Aunque el sistema global es eléctricamente neutro, la separación de carga da lugar a un efecto electrostático cuya fuerza se expresa por el momento dipolar eléctrico dado por
\[μ = q \times r \label{\(\PageIndex{5}\)}\]
Los momentos dipolares poseen tanto magnitud como dirección, y por lo tanto son cantidades vectoriales; están representados convencionalmente por flechas cuyas cabezas están en el extremo negativo.
Momentos dipolares permanentes
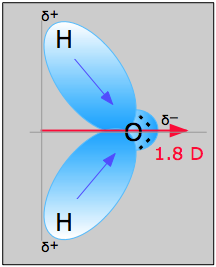
Estos son comúnmente referidos simplemente como “momentos dipolares”. La molécula más conocida que tiene un momento dipolar es el agua ordinaria. El desequilibrio de carga surge porque el oxígeno, con su carga nuclear de 8, tira de la nube de electrones que comprende cada enlace O-H hacia sí mismo. Estos dos “momentos de enlace” se suman vectorialmente para producir el momento dipolo permanente denotado por la flecha roja. Observe el uso del símbolo δ (delta griego) para denotar los extremos positivo y negativo de los dipolos.
Cuando un dipolo eléctrico se somete a un campo eléctrico externo, tenderá a orientarse para minimizar la energía potencial; es decir, su extremo negativo tenderá a apuntar hacia el potencial eléctrico más alto (más positivo). En líquidos, los movimientos térmicos actuarán para interrumpir este orden, por lo que el efecto general depende de la temperatura. En las fases condensadas los campos locales debidos a iones o dipolos cercanos en una sustancia juegan un papel importante en la determinación de las propiedades físicas de la sustancia, y es en este contexto que las interacciones dipolares son de interés para nosotros aquí. Discutiremos cada tipo de interacción en orden de disminución de la fuerza.
Dipolos inducidos
Incluso si una molécula es eléctricamente neutra y no posee un momento dipolar permanente, aún puede verse afectada por un campo eléctrico externo. Debido a que todos los átomos y moléculas están compuestos por partículas cargadas (núcleos y electrones), el campo eléctrico de un ion cercano hará que los centros de cargas positivas y negativas se desplacen en direcciones opuestas. Este efecto, que se llama polarización, da como resultado la creación de un momento dipolar temporal o inducido. El dipolo inducido interactúa entonces con las especies que lo produjeron, dando como resultado una atracción neta entre las dos partículas.
Cuanto más grande sea un átomo o ion, más flojamente sostenidos son sus electrones externos, y más fácilmente será la nube de electrones distorsionada por un campo externo. Una cantidad conocida como polarizabilidad expresa la magnitud del dipolo temporal que puede ser inducido en él por una carga cercana.
Interacciones ión-dipolo
Un dipolo cercano a un ion positivo o negativo se orientará de manera que el extremo cuya carga parcial sea opuesta a la carga iónica apunte hacia el ion. Este tipo de interacción es muy importante en soluciones acuosas de sustancias iónicas; H 2 O es una molécula altamente polar, por lo que en una solución de cloruro de sodio, por ejemplo, los iones Na + serán envueltos por una capa de moléculas de agua con sus extremos de oxígeno apuntando hacia estos iones, mientras que las moléculas de H 2 O que rodean a los iones Cl — tendrán sus extremos de hidrógeno dirigidos hacia adentro. Como consecuencia de las interacciones ión-dipolo, todas las especies iónicas en solución acuosa se hidratan; esto es lo que se denota con el sufijo en fórmulas como K + (aq), etc.
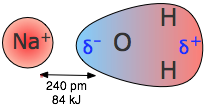
La fuerza de atracción ión-dipolo depende de la magnitud del momento dipolar y de la densidad de carga del ión. Esta última cantidad es apenas la carga del ion dividida por su volumen. Debido a sus tamaños más pequeños, los iones positivos tienden a tener densidades de carga mayores que los iones negativos, y deben estar más fuertemente hidratados en solución acuosa. El ion hidrógeno, al ser nada más que un protón desnudo de volumen extremadamente pequeño, tiene la mayor densidad de carga de cualquier ion; es por esta razón que existe completamente en su forma hidratada H 3 O + en agua.
Interacciones dipolo-dipolo
A medida que dos dipolos se acercan, tenderán a orientarse de manera que sus extremos con carga opuesta sean adyacentes. Dos de tales disposiciones son posibles: los dipolos pueden estar uno al lado del otro pero apuntando en direcciones opuestas, o pueden ser de extremo a extremo. Se puede demostrar que la disposición de extremo a extremo da una menor energía potencial.
La atracción dipolo-dipolo es más débil que la atracción ión-dipolo, pero aún puede tener efectos significativos si los momentos dipolares son grandes. El ejemplo más importante de atracción dipolo-dipolo es el enlace de hidrógeno.
Interacciones dipolo inducidas por iones
Los efectos dipolares inducidos más significativos son el resultado de iones cercanos, particularmente cationes (iones positivos). Los iones cercanos pueden distorsionar las nubes de electrones incluso en moléculas polares, cambiando así temporalmente sus momentos dipolares. Los iones más grandes (especialmente los negativos como SO 2 - y ClO 4 2—) son altamente polarizables, y los momentos dipolares inducidos en ellos por un catión pueden desempeñar un papel dominante en la formación de compuestos.
Interacciones dipolares inducidas por dipolo
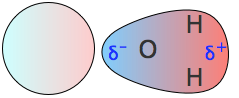
Un dipolo permanente puede inducir uno temporal en una especie que normalmente no es polar, y así producir una fuerza neta de atracción entre las dos partículas (Figura\(\PageIndex{9}\)). Esta atracción suele ser bastante débil, pero en algunos casos puede conducir a la formación de compuestos poco unidos. Este efecto explica la observación por otra parte sorprendente de que una amplia variedad de moléculas neutras como los hidrocarburos, e incluso algunos de los elementos de gas noble, forman compuestos hidratados estables con el agua.
Fuerzas de Dispersión (Londres)
El hecho de que elementos de gas noble y moléculas completamente no polares como H 2 y N 2 puedan condensarse en líquidos o sólidos nos dice que debe haber otra fuente de atracción entre partículas que no dependa de la existencia de momentos dipolares permanentes en ninguno de los dos partícula (Figura\(\PageIndex{10}\)). Para entender el origen de este efecto, es necesario darse cuenta de que cuando decimos que una molécula es “no polar”, realmente queremos decir que el momento dipolar promediado en el tiempo es cero. Este es el mismo tipo de promediación que hacemos cuando dibujamos una imagen de un orbital, que representa todas las ubicaciones en el espacio en las que se puede encontrar un electrón con cierta probabilidad mínima. En una escala de tiempo muy corta, sin embargo, el electrón debe estar cada vez más localizado; ni siquiera la mecánica cuántica le permite estar en más de un lugar en un instante dado. En consecuencia, no hay garantía de que la distribución de la carga negativa alrededor del centro de un átomo sea perfectamente simétrica en cada instante; cada átomo tiene, por lo tanto, un momento dipolar débil, fluctuante, que está continuamente desapareciendo y reapareciendo en otra dirección.
Las fuerzas de dispersión o Londres pueden considerarse interacciones de “dipolo espontáneo - dipolo inducido”.
Aunque estas fluctuaciones extremadamente efímeras promedian rápidamente a cero, aún pueden inducir nuevos dipolos en un átomo o molécula vecina, lo que ayuda a sostener el dipolo original y da lugar a una débil fuerza atractiva conocida como la dispersión o fuerza londinense. Aunque las fuerzas de dispersión son las más débiles de todas las atracciones intermoleculares, están universalmente presentes. Su fuerza depende en gran medida del número de electrones en una molécula. Esto se puede ver claramente observando los elementos de gas noble en la Tabla\(\PageIndex{2}\), cuya capacidad de condensarse a líquidos y congelarse a sólidos depende completamente de las fuerzas de dispersión.
| elemento | Él | Ne | Ar | Kr | Xe |
|---|---|---|---|---|---|
| número atómico | 2 | 10 | 18 | 36 | 54 |
| punto de ebullición, K | 27 | 87 | 120 | 165 | 211 |
| temperatura crítica, K | 5 | 44 | 151 | 209.5 | 290 |
| calor de vaporización, kJ mol —1 | 0.08 | 1.76 | 6.51 | 59 | 12.6 |
Es importante señalar que las fuerzas de dispersión son aditivas; si dos moléculas alargadas se encuentran lado a lado, las atracciones de fuerza de dispersión existirán a lo largo de las regiones donde las dos moléculas están cerca. Esto puede producir atractivos bastante fuertes entre moléculas poliméricas grandes incluso en ausencia de fuerzas de atracción más fuertes.
“van der Waals” fuerzas es una captura todo Término
Aunque las moléculas no polares no son en absoluto infrecuentes, muchos tipos de moléculas poseen momentos dipolares permanentes, por lo que los líquidos y sólidos compuestos de estas especies se mantendrán unidos por una combinación de dipolo-dipolo, dipolo inducido por dipolo y fuerzas de dispersión. Estas fuerzas más débiles (es decir, las que no sean atracciones coulómbicas) se conocen colectivamente como fuerzas de van der Waals. Estos incluyen atracción y repulsiones entre átomos, moléculas y superficies, así como otras fuerzas intermoleculares. El término incluye:
- fuerza entre dos dipolos permanentes y momentos de orden superior como cuadrupolo
- fuerza entre un dipolo permanente y un dipolo inducido correspondiente
- fuerza entre dos dipolos inducidos instantáneamente (fuerzas de dispersión)
El cuadro\(\PageIndex{3}\) muestra algunas estimaciones de las contribuciones de los diversos tipos de fuerzas de van der Waals que actúan entre varios tipos diferentes de moléculas. Obsérvese particularmente cuán importantes son las fuerzas de dispersión en todos estos ejemplos, y cómo esto, a su vez, depende de la polarizabilidad.
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|
| Ar | —186 | 0 | 1.6 | 0 | 0 | 100 |
| CO | —190 | 0.1 | 2.0 | 0 | 0 | 100 |
| HCl | —84 | 1.0 | 2.6 | 4.2 | 14.4 | 81.4 |
| HBr | —67 | 0.8 | 3.6 | 2.2 | 3.3 | 94.5 |
| HOLA | —35 | 0.4 | 5.4 | 0.4 | 0.1 | 99.5 |
| NH 3 | —33 | 1.5 | 2.6 | 5.4 | 44.6 | 50.0 |
| H 2 O | 100 | 1.8 | 1.5 | 4.0 | 77.0 | 19.0 |