8.7: Propiedades coligativas y Entropía

Los cuatro efectos de la solución (presión de vapor reducida, depresión del punto de congelación, elevación del punto de ebullición, presión osmótica) resultan de la “dilución” del disolvente por el soluto agregado. Debido a esta comunalidad se les conoce como propiedades coligativas (Lat. co ligare, conectado a.) El papel clave de la concentración de disolvente se ve oscurecido por las expresiones muy simplificadas utilizadas para calcular la magnitud de estos efectos, en las que solo aparece la concentración de soluto. Los detalles de cómo llevar a cabo estos cálculos y las muchas aplicaciones importantes de las propiedades coligativas se cubren en otra parte. Nuestro propósito aquí es ofrecer una explicación más completa de por qué ocurren estos fenómenos.

Básicamente, todos estos resultan del efecto de dilución del disolvente sobre su entropía, y así en el incremento en la densidad de estados energéticos del sistema en la solución respecto a la del líquido puro. El equilibrio entre dos fases (líquido-gas para ebullición y sólido-líquido para congelación) ocurre cuando los estados energéticos en cada fase pueden ser poblados a densidades iguales. Las temperaturas a las que esto ocurre son representadas por el sombreado.

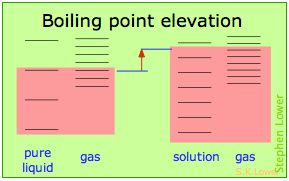
• La dilución del solvente agrega nuevos estados de energía al líquido, pero no afecta la fase de vapor. Esto eleva la temperatura requerida para hacer accesibles números iguales de microestados en las dos fases.
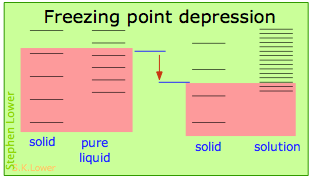
• La dilución del solvente agrega nuevos estados de energía al líquido, pero no afecta a la fase sólida. Esto reduce la temperatura requerida para hacer accesible el mismo número de estados en las dos fases.

Efectos de la presión sobre la entropía: Presión osmótica

Cuando un líquido es sometido a presión hidrostática, por ejemplo, por un gas inerte y no disolvente que ocupa el espacio de vapor por encima de la superficie, se eleva la presión de vapor del líquido. La presión actúa comprimiendo el líquido muy ligeramente, estrechando efectivamente el pozo de energía potencial en el que residen las moléculas individuales y aumentando así su tendencia a escapar de la fase líquida. (Debido a que los líquidos no son muy compresibles, el efecto es bastante pequeño; una presión aplicada de 100 atm elevará la presión de vapor del agua a 25°C en solo aproximadamente 2 torr.) En cuanto a la entropía, podemos decir que la presión aplicada reduce las dimensiones de la “caja” dentro de la cual los principales movimientos de traslación de las moléculas están confinados dentro del líquido, reduciendo así la densidad de estados energéticos en la fase líquida.

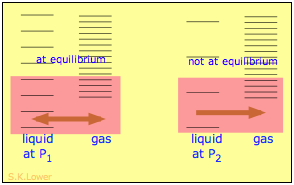
La aplicación de presión hidrostática a un líquido aumenta el espaciamiento de sus microestados, de manera que el número de estados energéticamente accesibles en el gas, aunque sin cambios, es relativamente mayor, aumentando así la tendencia de las moléculas a escapar a la fase vapor. En términos de energía libre, la mayor presión eleva la energía libre del líquido, pero no afecta la de la fase gaseosa.

Este fenómeno puede explicar la presión osmótica. La presión osmótica, se debe recordar a los estudiantes, no es lo que impulsa la ósmosis, sino más bien la presión hidrostática que se debe aplicar a la solución más concentrada (disolvente más diluido) para detener el flujo osmótico de disolvente hacia la solución. El efecto de esta presión\(\Pi\) es aumentar ligeramente el espaciamiento de los estados de energía del solvente en el lado de alta presión (diluido-solvente) de la membrana para que coincida con el del solvente puro, restaurando el equilibrio osmótico.

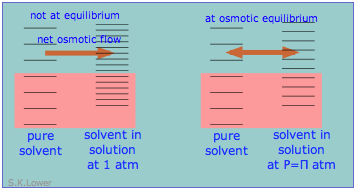
La presión osmótica no impulsa la ósmosis, sino que es la presión hidrostática que se debe aplicar a la solución más concentrada (disolvente más diluido) para detener el flujo osmótico de disolvente hacia la solución.