14.6: Aplicaciones de la Termoquímica
- Page ID
- 70626
Prácticamente todos los procesos químicos implican la absorción o liberación de calor, y así cambios en la energía interna del sistema. En esta sección, estudiamos algunas de las aplicaciones más comunes relacionadas con la química de la entalpía y la Primera Ley. Si bien las dos primeras secciones se refieren principalmente a la química, las restantes impactan en la vida cotidiana de todos.
Diagramas de entalpía y sus usos
La comparación e interpretación de los cambios de entalpía está materialmente ayudada por una construcción gráfica en la que las entalpías relativas de diversas sustancias están representadas por líneas horizontales en una escala de energía vertical. El cero de la escala se puede colocar en cualquier lugar, ya que las energías son siempre arbitrarias; generalmente es más útil ubicar los elementos en energía cero, lo que refleja la convención de que sus entronicias estándar de formación son cero.
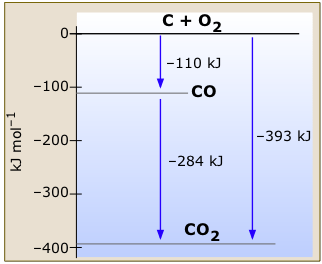
Este diagrama de entalpía muy simple para carbono y oxígeno y sus dos óxidos estables (Figura\(\PageIndex{1}\)) muestra los cambios en la entalpía asociados a las diversas reacciones que puede sufrir este sistema. Observe cómo la ley de Hess está implícita en este diagrama; podemos calcular el cambio de entalpía para la combustión de monóxido de carbono a dióxido de carbono, por ejemplo, restando las longitudes de flecha apropiadas sin escribir las ecuaciones termoquímicas de manera formal.
Los estados de referencia de entalpía cero se refieren al grafito, la forma más estable de carbono, y al oxígeno gaseoso. Todas las temperaturas son 298 K.
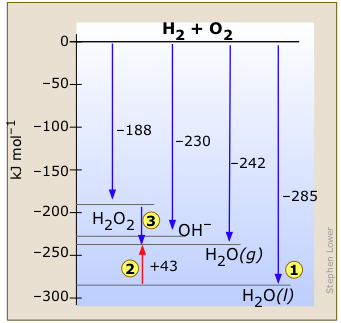
Este diagrama de entalpía para el sistema hidrógeno-oxígeno (Figura\(\PageIndex{2}\)) muestra las configuraciones estables conocidas de estos dos elementos. La reacción de H 2 y O 2 gaseosos para producir un mol de agua líquida libera 285 kJ de calor
. Si el H 2 O se forma en estado gaseoso, la liberación de energía será menor. Observe también que...
- El calor de vaporización del agua
(un proceso endotérmico) se encuentra claramente en el diagrama. - El peróxido de hidrógeno H 2 O 2, que se descompone espontáneamente en O 2 y H 2 O, libera algo de calor
en este proceso. Normalmente esta reacción es tan lenta que no se nota el calor. Pero el uso de un catalizador apropiado puede hacer que la reacción sea tan rápida que se haya utilizado para alimentar un auto de carreras.
Por qué no puedes correr tu auto en el agua
Es posible que hayas escuchado la venerable leyenda urbana, probablemente a estas alturas de más de 80 años, de que algún oscuro inventor descubrió un proceso para hacerlo, pero la invención fue comprada secretamente por las petroleras para preservar su monopolio. El diagrama de entalpía para el sistema hidrógeno-oxígeno muestra por qué esto no puede ser cierto; simplemente no hay ningún compuesto conocido de H y O que resida a un nivel de entalpía más bajo.
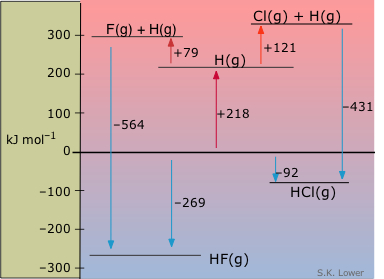
Los diagramas de entalpía son especialmente útiles para comparar grupos de sustancias que tienen alguna característica común. Esta muestra las entalpías molares de especies relacionadas con dos haluros de hidrógeno, con respecto a las de los elementos. A partir de este diagrama podemos ver de un vistazo que la formación de HF a partir de los elementos es considerablemente más exotérmica que la formación correspondiente de HCl. La parte superior de este diagrama muestra los átomos gaseosos en entalpías positivas con respecto a los elementos. Se puede imaginar que los procesos endotérmicos en los que el H 2 y el dihalógeno se disocian en átomos se llevan a cabo en dos etapas, también se muestra. A partir del cambio de entalpía asociado a la disociación de H 2 (218 kJ mol —1), las entalpías de disociación de F 2 y Cl 2 pueden calcularse y colocarse en el diagrama.
Entalpías de enlace vs. energías de enlace
El cambio de entalpía asociado a la reacción
\[\ce{HI(g) → H(g) + I(g)}\]
es la entalpía de disociación de la\(\ce{HI}\) molécula; también es la energía de enlace del enlace hidrógeno-yodo en esta molécula. Bajo las condiciones estándar habituales, se expresaría ya sea como la entalpía de enlace H° (HI,298K) o la energía interna U° (HI,298); en este caso las dos cantidades difieren entre sí por Δ PV = RT. Dado que esta reacción no puede estudiarse directamente, la entalpía del enlace H-I se calcula a partir de las entalpías estándar apropiadas de formación:
| ½ H 2 (g) → H (g) | + 218 kJ |
| ½ I 2 (g) → I (g) | +107 kJ |
| ½ H 2 (g) + 1/2 I 2 (g) → HI (g) | —36 kJ |
| HI (g) → H (g) + I (g) | +299 kJ |
Las energías de enlace y las entalpías son propiedades importantes de los enlaces químicos, y es muy importante poder estimar sus valores a partir de otros datos termoquímicos. La entalpía de enlace total de una molécula más compleja como el etano se puede encontrar a partir de la siguiente combinación de reacciones:
| C 2 H 6 (g) → 2C (grafito) + 3 H 2 (g) | 84.7 kJ |
| 3 H 2 (g) → 6 H (g) | 1308 kJ |
| 2 C (grafito) → 2 C (g) | 1430 kJ |
| C 2 H 6 (g) → 2 C (g) + 6H (g) | 2823 kJ |
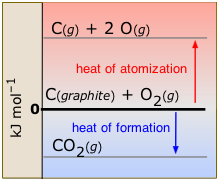
Cuando una molécula en su estado ordinario se descompone en átomos gaseosos, el proceso se conoce como atomización (Figura\(\PageIndex{4}\)). La entalpía estándar de atomización se refiere a la transformación de un elemento en átomos gaseosos:
\[\ce{ C_{(graphite)} → C(g)} \;\;\;\; ΔH^o = 716.7\; kJ\]
La atomización es siempre un proceso endotérmico. Los calores de atomización son los más utilizados para calcular las energías de enlace. Por lo general, se miden espectroscópicamente.
Regla de Pauling y Energía Promedio de Bonos
Regla de Pauling
La energía de enlace total de una molécula puede considerarse como la suma de las energías de los enlaces individuales.
La Regla de Pauling es sólo una aproximación, porque la energía de un determinado tipo de enlace no es realmente una constante, sino que depende algo del entorno químico particular de los dos átomos. Es decir, de lo único que realmente podemos hablar es de la energía promedio de un tipo particular de enlace, como C—O, por ejemplo, tomándose el promedio sobre una muestra representativa de compuestos que contienen este tipo de enlace, como CO, CO 2, COCl 2, (CH 3) 2 CO, CH 3 COOH, etc.
A pesar de la falta de estricta aditividad de las energías de enlace, la Regla de Pauling es sumamente útil porque permite estimar los calores de formación de compuestos que no han sido estudiados, o que ni siquiera se han preparado. Así, en el ejemplo anterior, si conocemos las entalpías de los enlaces C—C y C—H a partir de otros datos, podríamos estimar la entalpía de enlace total del etano, y luego trabajar de nuevo para obtener alguna otra cantidad de interés, como la entalpía de formación del etano. Al ensamblar una gran cantidad de información experimental de este tipo, se puede obtener un conjunto consistente de energías de enlace promedio. Las energías de los dobles enlaces son mayores que las de los enlaces simples, y las de los enlaces triples son aún mayores (Cuadro\(\PageIndex{1}\)).
| H | C | N | O | F | Cl | Br | I | Si | |
|---|---|---|---|---|---|---|---|---|---|
| H | 436 | 415 | 390 | 464 | 569 | 432 | 370 | 295 | 395 |
| C | 345 | 290 | 350 | 439 | 330 | 275 | 240 | 360 | |
| N | 160 | 200 | 270 | 200 | 270 | ||||
| O | 140 | 185 | 205 | 185 | 200 | 370 | |||
| F | 160 | 255 | 160 | 280 | 540 | ||||
| Cl | 243 | 220 | 210 | 359 | |||||
| Br | 190 | 180 | 290 | ||||||
| I | 150 | 210 | |||||||
| Si | 230 |
Contenido Energético de Combustibles
Un combustible es cualquier sustancia capaz de proporcionar cantidades útiles de energía a través de un proceso que puede llevarse a cabo de manera controlada a un costo económico. Para la mayoría de los combustibles prácticos, el proceso es la combustión en aire (en la que el agente oxidante O 2 está disponible a costo cero.) La entalpía de combustión es obviamente un criterio importante para la idoneidad de una sustancia como combustible, pero no es el único; un combustible útil también debe encenderse fácilmente, y en el caso de un combustible destinado a vehículos autopropulsados, su densidad energética en términos de ambas masas (kJ kg —1) y el volumen (kJ m —3) deben ser razonablemente grandes. Por lo tanto, las sustancias como el metano y el propano que son gases a 1 atm deben almacenarse como líquidos presurizados para su transporte y aplicaciones portátiles.
|
|
|
|---|---|
| madera (seca) | 15 |
| carbón (pobre) | 15 |
| carbón (premium) | 27 |
| etanol a | 30 |
| productos derivados del petróleo | 45 |
| metano, gas natural licuado | 54 |
| hidrógeno b | 140 |
Notas sobre la tabla anterior
a El etanol está siendo fuertemente promovido como combustible para motores por la industria agrícola estadounidense. Tenga en cuenta, sin embargo, que según algunas estimaciones, se necesitan 46 MJ de energía para producir 1 kg de etanol a partir del maíz. Algunos otros análisis, que toman en cuenta prácticas óptimas de cultivo y el uso de subproductos, llegan a diferentes conclusiones; véase, por ejemplo, este resumen con enlaces a varios reportes.
b Debido a su baja masa molar y alto calor de combustión, el hidrógeno posee una densidad de energía extraordinariamente alta, y sería un combustible ideal si su temperatura crítica (33 K, temperatura por encima de la cual no puede existir como líquido) no fuera tan baja. Los beneficios potenciales de usar hidrógeno como combustible han motivado una gran cantidad de investigación sobre otros métodos para obtener una gran cantidad de H 2 en un pequeño volumen de espacio. Simplemente comprimir el gas a una presión muy alta no es práctico porque el peso del recipiente de acero de pared gruesa requerido para soportar la presión aumentaría el peso efectivo del combustible a un valor inaceptablemente grande. Un esquema que ha mostrado algunas promesas explota la capacidad de H 2 para “disolverse” en ciertos metales de transición. El hidrógeno se puede recuperar de la solución sólida resultante (en realidad un compuesto poco unido) por calentamiento.
Contenido energético de los alimentos
¿Qué, exactamente, se entiende por la afirmación de que un alimento en particular “contiene 1200 calorías” por porción? Esto simplemente se refiere a la entalpía estándar de combustión del producto alimenticio, medida en un calorímetro de bomba. Nótese, sin embargo, que en el uso nutricional, la caloría es realmente una kilocaloría (a veces llamada “gran caloría”), es decir, 4184 J. Aunque esta unidad todavía se emplea en la literatura popular, la unidad SI es ahora de uso común en la literatura científica y clínica, en la que los contenidos energéticos de los alimentos suelen cotizarse en kJ por unidad de peso.
Si bien los mecanismos de oxidación de un carbohidrato como la glucosa a dióxido de carbono y agua en un calorímetro de bomba y en el cuerpo son complejos y completamente diferentes, la reacción neta involucra los mismos estados inicial y final, y debe ser el mismo para cualquier vía posible:
\[C_6H_{12}O_6 + 6 O_2 → 6 CO_2 + 6 H_2O \;\;\;\; ΔH^o = – 20.8\; kJ \;mol^{–1}\]
La glucosa es un azúcar, un producto de descomposición del almidón, y es la fuente de energía más importante a nivel celular; las grasas, proteínas y otros azúcares se convierten fácilmente en glucosa. Al escribir ecuaciones equilibradas para la combustión de azúcares, grasas y proteínas, se puede hacer una comparación de sus contenidos energéticos relativos. La estequiometría de cada reacción da las cantidades de oxígeno absorbidas y liberadas cuando se oxida una cantidad dada de cada tipo de alimento; estos volúmenes de gas a menudo se toman como medidas indirectas de consumo de energía y actividad metabólica; un valor comúnmente aceptado que parece aplicarse a una variedad de fuentes de alimentos es de 20.1 J (4.8 kcal) por litro de O 2 consumido.
Para algunos componentes de los alimentos, particularmente las proteínas, la oxidación puede no ser siempre completa en el cuerpo, por lo que la energía que realmente está disponible será menor que la dada por el calor de la combustión. Los mamíferos, por ejemplo, son incapaces de descomponer la celulosa (un polímero de azúcar) en absoluto; los animales que obtienen una parte importante de su nutrición a partir del pasto y las hojas deben depender de la acción de bacterias simbióticas que colonizan sus tractos digestivos. La cantidad de energía disponible de un alimento se puede encontrar midiendo el calor de combustión de los productos de desecho excretados por un organismo que ha sido restringido a una dieta controlada, y restando esto del calor de combustión del alimento (Tabla\(\PageIndex{3}\)).
| tipo de alimento | comida |
ΔH° (kJ g —1) |
disponibilidad porcentual |
|---|---|---|---|
| Proteína | carne | 22.4 | 92 |
| huevo | 23.4 | ||
| Grasa | mantequilla | 38.2 | |
| grasa animal | 39.2 | 95 | |
| Carbohidratos | almidón | 17.2 | |
| glucosa (azúcar) | 15.5 | 99 | |
| etanol | 29.7 | 100 |
La cantidad de energía que requiere un animal depende de la edad, el sexo, la superficie del cuerpo y por supuesto de la cantidad de actividad física. La velocidad a la que se consume la energía se expresa en vatios: 1 W = 1 J seg —1. Para los humanos, este valor varía de aproximadamente 200-800 W. Esto se traduce en ingestas diarias de alimentos que tienen equivalentes de energía de aproximadamente 10-15 MJ para la mayoría de los adultos que trabajan. Para simplemente mantener el peso en ausencia de cualquier actividad física, se requieren alrededor de 6 MJ por día.
| animal | kJ hr —1 | kJ kg —1 hr —1 |
|---|---|---|
| ratón | 82 | 17 |
| gato | 34 | 6.8 |
| perro | 78 | 3.3 |
| ovejas | 193 | 2.2 |
| humano | 300 | 2.1 |
| caballo | 1430 | 1.1 |
| elefante | 5380 | 0.7 |
La tabla anterior es instructiva en que aunque los animales más grandes consumen más energía, el consumo de energía por unidad de peso corporal disminuye con el tamaño. Esto refleja el hecho de que la tasa de pérdida de calor al ambiente depende en gran medida de la superficie de un animal, que aumenta con la masa a un ritmo mayor que lo hace el volumen de un animal (“tamaño”).
La termodinámica y el clima
Enlaces de hidrógeno en el trabajo
Es de conocimiento común que grandes masas de agua tienen un efecto “moderador” sobre el clima local, reduciendo los extremos de temperatura que ocurren en otras áreas. Las temperaturas del agua cambian mucho más lentamente que las del suelo, la roca y la vegetación, y este efecto tiende a afectar a las masas de tierra cercanas. Esto se debe en gran parte a la alta capacidad calorífica del agua en relación con la de las superficies terrestres y, en última instancia, a los efectos de los enlaces de hidrógeno. La menor eficiencia del agua como absorbedor y radiador de energía infrarroja también juega un papel importante.
La capacidad calorífica específica del agua es aproximadamente cuatro veces mayor que la del suelo. Esto tiene una consecuencia directa para cualquiera que viva cerca del océano y esté familiarizado con las variaciones diarias en la dirección de los vientos entre la tierra y el agua. Incluso los grandes lagos pueden ejercer una influencia moderadora en el clima local debido a la relativa insensibilidad del agua al cambio de temperatura.
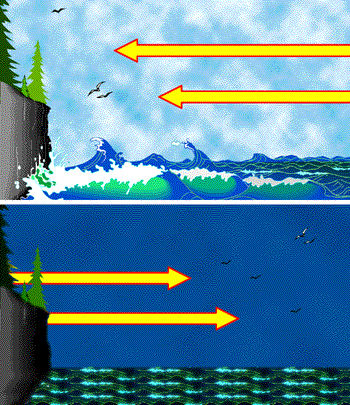
Durante el día la tierra y el mar reciben cantidades aproximadamente iguales de calor del Sol, pero la capacidad calorífica mucho menor de la tierra hace que su temperatura suba más rápidamente. Esto hace que el aire sobre la tierra se caliente, reduciendo su densidad y provocando que suba. Se asoma aire oceánico más fresco para llenar el vacío, dando lugar así a la brisa marina diurna. Por la noche, tanto la tierra como el océano pierden calor por radiación al cielo, pero la temperatura del agua desciende menos que la de la tierra, continuando suministrando calor al aire oceánico y provocando que suba, invirtiendo así la dirección del flujo de aire y produciendo la brisa terrestre vespertina.
Por qué hace más frío a medida que vas más alto: la tasa de lapso adiabático
El aire recibe su calor absorbiendo la radiación infrarroja lejana de la tierra, que por supuesto recibe su calor del sol. La cantidad de calor que se irradia al aire inmediatamente por encima de la superficie varía con lo que hay en él (bosque, campos, agua, edificios) y por supuesto con la época y la estación del año. Cuando un paquete de aire por encima de una ubicación particular pasa a calentarse más que el aire que lo rodea inmediatamente, este aire se expande y se vuelve menos denso. Por lo tanto, se eleva a través del aire circundante y experimenta una mayor expansión a medida que encuentra presiones más bajas a mayores altitudes.
Siempre que un gas se expande contra una presión opuesta, funciona en los alrededores. De acuerdo con la Primera Ley Δ U = q + w, si esta obra no va acompañada de un flujo compensador de calor hacia el sistema, su energía interna caerá, y así, por tanto, lo hará su temperatura. Resulta que el flujo de calor y la mezcla son procesos bastante lentos en la atmósfera en comparación con el movimiento convectivo que estamos describiendo, por lo que la Primera Ley puede escribirse como Δ U = w (recordemos que w es negativo cuando un gas se expande.) Así, a medida que el aire se eleva por encima de la superficie de la tierra experimenta expansión adiabática y se enfría. La tasa real de disminución de temperatura con la altitud depende de la composición del aire (siendo la variable principal su contenido de humedad) y de su capacidad calorífica. Para el aire seco, esto da como resultado una tasa de lapso adiabático de 9.8 C° por km de altitud.
Santa Anas y Chinooks
Justo lo contrario ocurre cuando los vientos se desarrollan en áreas de gran altitud y se dirigen cuesta abajo. A medida que el aire desciende, sufre compresión por la presión del aire por encima de él. El entorno ahora está trabajando en el sistema, y debido a que el proceso ocurre demasiado rápido para que el aumento de la energía interna se elimine como calor, la compresión es aproximadamente adiabática.
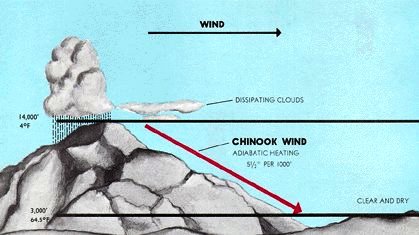
Los vientos resultantes son cálidos (y por lo tanto secos) y a menudo son muy irritantes para las membranas mucosas. Estos son conocidos genéricamente como vientos de Föhn (que es el nombre dado a los que se originan en los Alpes). En Norteamérica suelen llamarse chinooks (o, en invierno, “fundidores de nieve”) cuando se originan a lo largo de las Montañas Rocosas. Entre los más notorios se encuentran los vientos de Santa Ana del sur de California que recogen calor extra (y polvo) al pasar sobre el desierto de Mohave antes de sumergirse en la cuenca de Los Ángeles (Figura 13.5.X). Su sequedad y altas velocidades alimentan muchos de los desastrosos incendios forestales que afligen a la región.
