14.5: Calorimetría
- Page ID
- 70620
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Asegúrese de comprender a fondo el siguiente concepto esencial:
- Describir un calorímetro simple y explicar cómo se emplea y cómo se determina su capacidad calorífica.
La Calorimetría de Volumen Constante, también conocida como calorimetría de bomba, se utiliza para medir el calor de una reacción manteniendo constante el volumen y resistiendo grandes cantidades de presión. Aunque estos dos aspectos de la calorimetría de bombas permiten obtener resultados precisos, también contribuyen a la dificultad de la calorimetría de bombas. En este módulo se abordará el montaje básico de un calorímetro de bomba, así como cómo la calorimetría de la bomba se relaciona con el calor de reacción y la capacidad calorífica y los cálculos involucrados respecto a estos dos temas.
Introducción
La calorimetría se utiliza para medir cantidades de calor, y se puede utilizar para determinar el calor de una reacción a través de experimentos. Por lo general se utiliza un calorímetro de taza de café ya que es más sencillo que un calorímetro de bomba, pero para medir el calor evolucionado en una reacción de combustión, el volumen constante o la calorimetría de bomba es ideal. Un calorímetro de volumen constante también es más preciso que un calorímetro de taza de café, pero es más difícil de usar ya que requiere un recipiente de reacción bien construido que sea capaz de soportar grandes cantidades de cambios de presión que ocurren en muchas reacciones químicas.
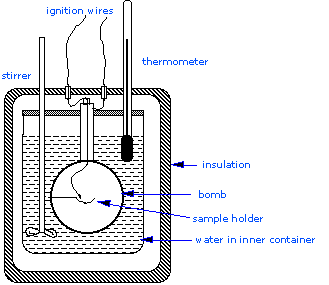
La calorimetría más grave que se lleva a cabo en laboratorios de investigación implica la determinación de calores de combustión\(\Delta H_{combustion}\), ya que estos son esenciales para la determinación de entalpías estándar de formación de los miles de nuevos compuestos que se preparan y caracterizan cada mes. En un calorímetro de volumen constante, el sistema está sellado o aislado de su entorno, lo que explica por qué su volumen es fijo y no se realiza ningún trabajo volumen-presión. Una estructura de calorímetro de bomba consta de lo siguiente:
- Bomba de acero que contiene los reactivos
- Baño de agua en el que se sumerge la bomba
- Termómetro
- Un agitador motorizado
- Alambre para encendido
Dado que el proceso se lleva a cabo a volumen constante, el recipiente de reacción debe construirse para soportar la alta presión resultante del proceso de combustión, lo que equivale a una explosión confinada. El buque suele llamarse “bomba”, y la técnica se conoce como calorimetría de bomba. La reacción se inicia mediante la descarga de un condensador a través de un cable delgado que enciende la mezcla.
Otra consecuencia de la condición de volumen constante es que el calor liberado corresponde a\(q_v\), y por lo tanto al cambio de energía interna\(ΔU\) más que a\(ΔH\). El cambio de entalpía se calcula de acuerdo con la fórmula
\[ΔH = q_v + Δn_gRT\]
donde\(Δn_g\) es el cambio en el número de moles de gases en la reacción.
Una muestra de bifenilo (\(\ce{(C6H5)2}\)) que pesaba 0.526 g se encendió en un calorímetro de bomba inicialmente a 25°C, produciendo un aumento de temperatura de 1.91 K. En un experimento de calibración separado, una muestra de ácido benzoico (\(\ce{C6H5COOH}\)) que pesaba 0.825 g se encendió en idénticas condiciones y produjo un aumento de temperatura de 1 .94 K. Para el ácido benzoico, se sabe que el calor de combustión a volumen constante es de 3,226 kJ mol —1 (es decir, Δ U = —3,226 kJ mol —1.) Utilice esta información para determinar la entalpía estándar de combustión de bifenilo.
Solución
Comience por elaborar la constante del calorímetro:
- Moles de ácido benzoico:
\[\dfrac{0.825 g}{122.1 \;g/mol} = 0.00676\; mol \nonumber\]
- Calor liberado al calorímetro:
\[(0.00676\; mol) \times (3226\; kJ/mol) = 21.80\; kJ \nonumber\]
- Constante del calorímetro:
\[\dfrac{21.80\; kJ}{1.94\; K} = 11.24\; kJ/K \nonumber\]
Ahora determinar\(ΔU_{combustion}\) del bifenilo (“BP”):
- moles de bifenilo:
\[\dfrac{0.526\; g}{154.12\; g/mol} = 0.00341 \; mol \nonumber\]
- calor liberado al calorímetro:
\[(1.91\; K) \times (11.24\; kJ/K) = 21.46\; kJ \nonumber\]
- calor liberado por mol de bifenilo:
\[\dfrac{21.46\; kJ}{0.00341\; mol} = 6,293\; kJ/mol \nonumber\]
\[ΔU_{combustion} (BP) = –6,293\; kJ/mol \nonumber\]
Este es el cambio de calor a volumen constante,\(q_v\) y el signo negativo indica que la reacción es exotérmica, como lo son todas las reacciones de combustión.
A partir de la ecuación de reacción equilibrada
\[\ce{(C6H5)2(s) + 29/2 O2(g) \rightarrow 12 CO2(g) + 5 H2O(l)} \nonumber\]
podemos calcular el cambio en los moles de gases para esta reacción
\[Δn_g = 12 - \frac{29}{2} = \frac{-5}{2} \nonumber\]
De esta manera, el volumen del sistema disminuye cuando tiene lugar la reacción. Al convertir a\(ΔH\), podemos escribir la siguiente ecuación. Adicionalmente, recordemos que a volumen constante,\(ΔU = q_V\).
\[ \begin{align*} ΔH &= q_V + Δn_gRT \\[4pt] &= ΔU -\left( \dfrac{5}{2}\right) (8.314\; J\; mol^{-1}\; K^{-1}) (298 \;K) \\[4pt] &= (-6,293 \; kJ/mol)–(6,194\; J/mol) \\[4pt] &= (-6,293-6.2)\;kJ/mol \\[4pt] &= -6299 \; kJ/mol \end{align*} \]
Un error común aquí es olvidar que el término restado está en J, no en kJ. Obsérvese que los 6.2 kJ adicionales en\(ΔH\) comparación con\(ΔU\) reflejan el trabajo que los alrededores realizan en el sistema a medida que el volumen de gases disminuye de acuerdo con la ecuación de reacción.
Determinar el calor de reacción
La cantidad de calor que el sistema cede a su entorno para que pueda regresar a su temperatura inicial es el calor de reacción. El calor de reacción es solo el negativo de la energía térmica ganada por el calorímetro y su contenido (\(q_{calorimeter}\)) a través de la reacción de combustión.
\[q_{rxn} = -q_{calorimeter} \label{2A}\]
donde
\[q_{calorimeter} = q_{bomb} + q_{water} \label{3A}\]
Si el calorímetro de volumen constante se configura de la misma manera que antes, (misma bomba de acero, misma cantidad de agua, etc.) entonces la capacidad calorífica del calorímetro se puede medir usando la siguiente fórmula:
\[q_{calorimeter} = \text{( heat capacity of calorimeter)} \times \Delta{T} \label{4A}\]
La capacidad calorífica se define como la cantidad de calor necesaria para aumentar la temperatura de todo el calorímetro en 1 °C. La ecuación anterior también se puede utilizar para calcular a\(q_{rxn}\) partir de\(q_{calorimeter}\) calculado por la Ecuación\ ref {2A}. La capacidad calorífica del calorímetro se puede determinar mediante la realización de un experimento.
1.150 g de sacarosa pasan por combustión en un calorímetro de bomba. Si la temperatura subió de 23.42 °C a 27.64 °C y la capacidad calorífica del calorímetro es de 4.90 kJ/°C, entonces determinar el calor de combustión de la sacarosa,\(\ce{C12H22O11}\) (en kJ por mol de\(\ce{C12H22O11}\)).
Solución
Dado:
- masa de\(C_{12}H_{22}O_{11}\): 1.150 g
- \(T_{initial}\): 23.42°C
- \(T_{final}\):27.64°C
- Capacidad calorífica del calorímetro: 4.90 kJ/°C
Usando la ecuación\ ref {4A} para calcular\(q_{calorimeter}\):
\[\begin{align*} q_{calorimeter} &= (4.90\; kJ/°C) \times (27.64 - 23.42)°C \\[4pt] &= (4.90 \times 4.22) \;kJ = 20.7\; kJ \end{align*}\]
Enchufe en la ecuación\ ref {2A}:
\[\begin{align*} q_{rxn} &= -q_{calorimeter} \\[4pt] &= -20.7 \; kJ \; \end{align*}\]
Pero la pregunta pregunta por KJ/mol\(\ce{C12H22O11}\), así que esto necesita ser convertido:
\[\begin{align*}q_{rxn} &= \dfrac{-20.7 \; kJ}{1.150 \; g \; C_{12}H_{22}O_{11}} \\[4pt] &= \dfrac{-18.0 \; kJ}{g\; C_{12}H_{22}O_{11}} \end{align*}\]
Convertir a por Mole\(\ce{C12H22O11}\):
\[\begin{align*}q_{rxn} &= \dfrac{-18.0 \; kJ}{\cancel{g \; \ce{C12H22O11}}} \times \dfrac{342.3 \; \cancel{ g \; \ce{C12H22O11}}}{1 \; mol \; \ce{C12H22O11}} \\[4pt] &= \dfrac{-6.16 \times 10^3 \; kJ \;}{mol \; \ce{C12H22O11}} \end{align*}\]
“Calorímetro de Hielo”
Si bien la calorimetría es simple en principio, su práctica es un arte altamente exigente, especialmente cuando se aplica a procesos que ocurren lentamente o implican cambios de calor muy pequeños, como la germinación de semillas. Los calorímetros pueden ser tan simples como una taza de café de espuma plástica, que a menudo se usa en laboratorios estudiantiles. Los calorímetros de grado de investigación, capaces de detectar pequeños cambios de temperatura, tienen más probabilidades de ocupar mesas o incluso habitaciones enteras:
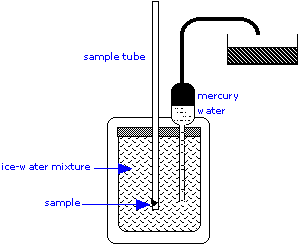
El calorímetro de hielo es una herramienta importante para medir las capacidades caloríficas de líquidos y sólidos, así como los calores de ciertas reacciones. Este sencillo pero ingenioso aparato es esencialmente un dispositivo para medir el cambio de volumen debido al derretimiento del hielo. Para medir una capacidad calorífica, se coloca una muestra caliente en el compartimiento interno, el cual está rodeado por una mezcla de hielo y agua.
El calor retirado de la muestra a medida que se enfría provoca que parte del hielo se derrita. Dado que el hielo es menos denso que el agua, el volumen de agua en la cámara aislada disminuye. Esto hace que un volumen equivalente de mercurio sea succionado hacia el depósito interno desde el contenedor exterior. La pérdida de peso de este recipiente da la disminución en el volumen del agua, y así la masa de hielo se fundió. Esto, combinado con el calor de fusión del hielo, da la cantidad de calor perdida por la muestra a medida que se enfría a 0°C.


