14.2: pH y pOH

Objetivos de aprendizaje

• Explicar la caracterización de las soluciones acuosas como ácidas, básicas o neutras
• Expresa las concentraciones de iones hidronio e hidróxido en las escalas de pH y PoH
• Realizar cálculos relacionados con pH y PoH

Como se discutió anteriormente, los iones hidronio e hidróxido están presentes tanto en agua pura como en todas las soluciones acuosas, y sus concentraciones son inversamente proporcionales según lo determinado por el producto iónico del agua (\(K_w\)). Las concentraciones de estos iones en una solución suelen ser determinantes críticos de las propiedades de la solución y los comportamientos químicos de sus otros solutos, y se ha desarrollado un vocabulario específico para describir estas concentraciones en términos relativos. Una solución es neutra si contiene concentraciones iguales de iones hidronio e hidróxido; ácida si contiene una mayor concentración de iones hidronio que iones hidróxido; y básica si contiene una concentración menor de iones hidronio que iones hidróxido.

Un medio común para expresar cantidades, cuyos valores pueden abarcar muchos órdenes de magnitud, es usar una escala logarítmica. Una escala de este tipo que es muy popular para las concentraciones químicas y las constantes de equilibrio se basa en la función p, definida como se muestra donde “X” es la cantidad de interés y “log” es el logaritmo de base 10:

\[\mathrm{pX=−\log X} \label{1} \]

Por lo tanto, el pH de una solución se define como se muestra aquí, donde [H ₃ O ⁺] es la concentración molar de ión hidronio en la solución:

\[\mathrm{pH=-\log[H_3O^+]}\label{\(\PageIndex{2}\)} \]

La reorganización de esta ecuación para aislar la molaridad del ion hidronio produce la expresión equivalente:

\[\mathrm{[H_3O^+]=10^{−pH}}\label{\(\PageIndex{3}\)} \]

Asimismo, la molaridad del ion hidróxido puede expresarse como una función p, o pOH:

\[\mathrm{pOH=-\log [OH^−]}\label{\(\PageIndex{4}\)} \]

o

\[\mathrm{[OH^-]=10^{−pOH}} \label{\(\PageIndex{5}\)} \]

Finalmente, la relación entre estas dos concentraciones de iones expresada como funciones p se deriva fácilmente de la\(K_w\) expresión:

\[K_\ce{w}=\ce{[H_3O^+][OH^- ]} \label{\(\PageIndex{6}\)} \]

\[-\log K_\ce{w}=\mathrm{-\log([H_3O^+][OH^−])=-\log[H_3O^+] + -\log[OH^-]}\label{\(\PageIndex{7}\)} \]

\[\mathrm{p\mathit{K}_w=pH + pOH} \label{\(\PageIndex{8}\)} \]

A 25 °C, el valor de\(K_w\) es\(1.0 \times 10^{−14}\), y así:

\[\mathrm{14.00=pH + pOH} \label{\(\PageIndex{9}\)} \]

La molaridad del ion hidronio en agua pura (o cualquier solución neutra) es de 25\( 1.0 \times 10^{-7}\; M\) °C, por lo que el pH y el pOH de una solución neutra a esta temperatura son:

\[\mathrm{pH=-\log[H_3O^+]=-\log(1.0\times 10^{−7}) = 7.00} \label{10} \]

\[\mathrm{pOH=-\log[OH^−]=-\log(1.0\times 10^{−7}) = 7.00} \label{11} \]

Y así, a esta temperatura, las soluciones ácidas son aquellas con molaridades de iones hidronio mayores que\( 1.0 \times 10^{-7}\; M\) y molaridades de iones hidróxido menores que\( 1.0 \times 10^{-7}\; M\) (correspondientes a valores de pH menores a 7.00 y valores de PoH mayores a 7.00). Las soluciones básicas son aquellas con molaridades de iones hidronio menores que\( 1.0 \times 10^{-7}\; M\) y molaridades de iones hidróxido mayores que\( 1.0 \times 10^{-7}\; M\) (correspondientes a valores de pH mayores a 7.00 y valores de PoH menores a 7.00).

Cuando\(pH=7\) Solutions are not Neutral

Dado que la constante\(K_w\) de autoionización depende de la temperatura, estas correlaciones entre los valores de pH y los adjetivos ácido/neutral/básico serán diferentes a temperaturas distintas de 25 °C, por ejemplo, la molaridad de hidronio del agua pura a 80 °C es de 4.9 × 10 ⁻⁷ M, que corresponde a valores de pH y pOH de:

\[\begin{align*} pH &=-\log[\ce{H_3O^+}] \\[4pt] &= -\log(4.9\times 10^{−7}) \\[4pt] &=6.31 \label{12} \end{align*} \]

\[\begin{align*} pOH &=-\log[\ce{OH^-}]\\[4pt] & =-\log(4.9\times 10^{−7}) \\[4pt] &=6.31 \label{13}\end{align*} \]

A esta temperatura, entonces, las soluciones neutras exhiben pH = pOH = 6.31, las soluciones ácidas exhiben pH menor a 6.31 y pOH mayor a 6.31, mientras que las soluciones básicas exhiben pH mayor a 6.31 y PoH menor a 6.31. Esta distinción puede ser importante a la hora de estudiar ciertos procesos que ocurren a temperaturas no estándar, como las reacciones enzimáticas en organismos de sangre caliente. A menos que se indique lo contrario, se presume que las referencias a los valores de pH son aquellas a temperatura estándar (25 °C) (Tabla\(\PageIndex{1}\)).

Tabla\(\PageIndex{1}\): Resumen de relaciones para soluciones ácidas, básicas y neutras

Clasificación	Concentraciones relativas de iones	pH a 25 °C
ácido	[H 3 O ^+] > [OH ^−]	pH < 7
neutral	[H 3 O ^+] = [OH ^−]	pH = 7
básico	[H 3 O ^+] < [OH ^−]	pH > 7

La figura\(\PageIndex{1}\) muestra las relaciones entre [H ₃ O ⁺], [OH ⁻], pH y PoH, y da valores para estas propiedades a temperaturas estándar para algunas sustancias comunes.

Figura\(\PageIndex{1}\): Las escalas de pH y PoH representan concentraciones de [H ₃ O ⁺] y OH ⁻, respectivamente. Los valores de pH y PoH de algunas sustancias comunes a temperatura estándar (25 °C) se muestran en este gráfico.

Se proporciona una tabla con 5 columnas. La primera columna está etiquetada como “corchete izquierdo H subíndice 3 O superíndice más corchete derecho (M)”. Poderes de diez se enumeran en la columna comenzando en 10 superíndice 1, incluyendo 10 superíndice 0 o 1, 10 superíndice negativo 1, disminuyendo por potencias individuales de 10 a 10 superíndice negativo 15. La segunda columna está etiquetada como “corchete izquierdo O H superíndice negativo corchete derecho (M)”. Poderes de diez se enumeran en la columna comenzando en 10 superíndice negativo 15, aumentando en potencias individuales de 10 para incluir 10 superíndice 0 o 1, y 10 superíndice 1. La tercera columna está etiquetada como “p H.” Los valores listados en esta columna son enteros que comienzan en 1 negativo, aumentando en unos hasta 14. La cuarta columna está etiquetada como “p O H.” Los valores de esta columna son enteros que comienzan en 15, disminuyendo por unos hasta 1 negativo. La quinta columna está etiquetada como “Solución de muestra”. Una línea vertical a la izquierda de la columna tiene marcas de graduación correspondientes a cada nivel p H de la tabla. Las sustancias se listan junto a este segmento de línea con segmentos de línea que las conectan a la línea para mostrar valores aproximados de p H y p O H. 1 M H C l se enumera a una p H de 0. Los jugos gástricos se listan a una p H de aproximadamente 1.5. El jugo de lima aparece en una p H de aproximadamente 2, seguido de 1 M C H subíndice 3 C O subíndice 2 H, seguido de ácido estomacal a un valor p H de casi 3. El vino aparece alrededor de 3.5. El café aparece justo después de las 5. El agua pura está listada a una p H de 7. La sangre pura está justo más allá de 7. Leche de Magnesia aparece justo después de una p H de 10.5. El amoníaco doméstico aparece justo antes de un pH de 12. 1 M N a O H aparece en una p H de 0. A la derecha de esta flecha etiquetada hay una flecha que apunta hacia arriba y hacia abajo a través de la altura de la columna. Una tira beige pasa por la mesa y a esta flecha de doble punta en p H 7. A la izquierda de la flecha de doble punta en esta tira beige se encuentra la etiqueta “neutral”. Una estrecha franja beige recorre la flecha. Justo arriba y debajo de esta región, la flecha es de color púrpura. Poco a poco se vuelve rojo brillante a medida que se extiende hacia arriba. En la parte superior de la flecha, cerca de la cabeza de la flecha se encuentra la etiqueta “ácida”. De igual manera, la región inferior cambia de color de púrpura a azul moviéndose a la parte inferior de la columna. La cabeza en este extremo de la flecha está etiquetada como “básica”.

Ejemplo\(\PageIndex{1}\): Calculation of pH from \(\ce{[H_3O^+]}\)

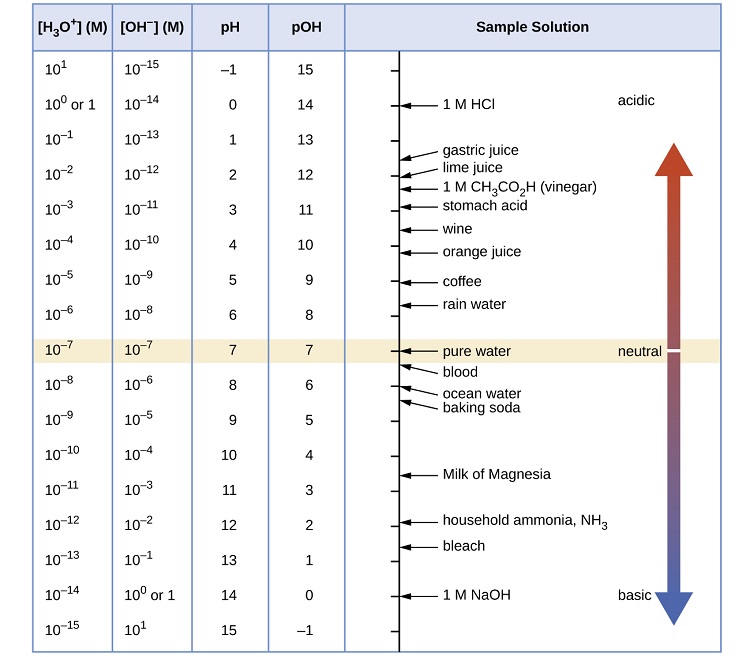
¿Cuál es el pH del ácido estomacal, una solución de HCl con una concentración de iones hidronio de\(1.2 \times 10^{−3}\; M\)?

Solución

\[\begin{align*} pH &=-\log [H_3O^+] \\[4pt] &= -\log(1.2 \times 10^{−3}) \\[4pt] &=−(−2.92) \\[4pt]&=2.92 \end{align*} \nonumber \]

Ejercicio\(\PageIndex{1}\)

El agua expuesta al aire contiene ácido carbónico, H ₂ CO ₃, debido a la reacción entre el dióxido de carbono y el agua:

\[\ce{CO2(aq) + H2O (l) \rightleftharpoons H2CO3(aq)} \nonumber \]

El agua saturada de aire tiene una concentración de iones hidronio causada por la disolución\(\ce{CO_2}\) de\(2.0 \times 10^{−6}\; M\), aproximadamente 20 veces mayor que la del agua pura. Calcular el pH de la solución a 25 °C.

Contestar

5.70

Ejemplo\(\PageIndex{2}\): Calculation of Hydronium Ion Concentration from pH

Calcular la concentración de iones hidronio en sangre, cuyo pH es 7.3 (ligeramente alcalino).

Solución

\[\mathrm{pH=-\log[H_3O^+]=7.3} \nonumber \]

\[\mathrm{\log[H_3O^+]=−7.3} \nonumber \]

\[\mathrm{[H_3O^+]=10^{−7.3}} \nonumber \]

o

\[[\ce{H_3O^+}]=\textrm{antilog of} −7.3 \nonumber \]

\[[\ce{H_3O^+}]=5\times 10^{−8}\;M \nonumber \]

(En una calculadora tome el antilog, o el log “inverso”, de −7.3, o calcule 10 ^−7.3).

Ejercicio\(\PageIndex{2}\)

Calcular la concentración de iones hidronio de una solución con un pH de −1.07.

Contestar

12 M

Ciencias Ambientales

El agua de lluvia normal tiene un pH entre 5 y 6 debido a la presencia de CO ₂ disuelto que forma ácido carbónico:

\[\ce{H2O (l) + CO2(g) ⟶ H2CO3(aq)} \label{14} \]

\[\ce{H2CO3(aq) \rightleftharpoons H^+(aq) + HCO3^- (aq)} \label{15} \]

La lluvia ácida es el agua de lluvia que tiene un pH inferior a 5, debido a que una variedad de óxidos no metálicos, incluyendo CO ₂, SO ₂, SO ₃, NO y NO ₂ se disuelven en el agua y reaccionan con ella para formar no solo ácido carbónico, sino ácido sulfúrico y ácido nítrico. La formación y posterior ionización de ácido sulfúrico se muestran aquí:

\[\ce{H2O (l) + SO3(g) ⟶ H2SO4(aq)} \label{16} \]

\[\ce{H2SO4(aq) ⟶ H^+(aq) + HSO4^- (aq)} \label{17} \]

El dióxido de carbono está naturalmente presente en la atmósfera porque nosotros y la mayoría de los otros organismos lo producimos como un producto de desecho del metabolismo. El dióxido de carbono también se forma cuando los incendios liberan carbono almacenado en la vegetación o cuando quemamos madera o combustibles fósiles. El trióxido de azufre en la atmósfera es producido naturalmente por la actividad volcánica, pero también proviene de la quema de combustibles fósiles, que tienen rastros de azufre, y del proceso de “tostado” de minerales de sulfuros metálicos en procesos de refinación de metales. Los óxidos de nitrógeno se forman en motores de combustión interna donde las altas temperaturas hacen posible que el nitrógeno y el oxígeno en el aire se combinen químicamente.

La lluvia ácida es un problema particular en áreas industriales donde los productos de combustión y fundición se liberan al aire sin ser despojados de óxidos de azufre y nitrógeno. En América del Norte y Europa hasta la década de 1980, fue responsable de la destrucción de bosques y lagos de agua dulce, cuando la acidez de la lluvia en realidad mató árboles, dañó el suelo e hizo que los lagos fueran inhabitables para todas las especies excepto para las más tolerantes a los ácidos. La lluvia ácida también corroe las fachadas estatuarias y de edificios que están hechas de mármol y piedra caliza (Figura\(\PageIndex{2}\)). Las regulaciones que limitan la cantidad de óxidos de azufre y nitrógeno que pueden ser liberados a la atmósfera por la industria y los automóviles han reducido la severidad del daño ácido tanto en ambientes naturales como artificiales en América del Norte y Europa. Ahora es un problema creciente en las zonas industriales de China e India.

Figura\(\PageIndex{2}\): (a) La lluvia ácida hace que los árboles sean más susceptibles a la sequía y la infestación de insectos, y agota los nutrientes en el suelo. b) También se corroe estatuas que están talladas en mármol o piedra caliza. (crédito a: modificación de obra de Chris M Morris; crédito b: modificación de obra por “Eden, Janine y Jim” /Flickr)

Se muestran dos fotos. La fotografía a de la izquierda muestra la porción superior de los árboles contra un cielo azul brillante. Las copas de varios árboles en el centro de la fotografía tienen ramas desnudas y parecen estar muertas. La imagen b muestra una estatua de un hombre que aparece desde la época de la guerra revolucionaria ya sea en mármol o piedra caliza.

Ejemplo\(\PageIndex{3}\): Calculation of pOH

¿Cuáles son el PoH y el pH de una solución 0.0125-M de hidróxido de potasio, KOH?

Solución

El hidróxido de potasio es un compuesto iónico altamente soluble y se disocia completamente cuando se disuelve en solución diluida, produciendo [OH ⁻] = 0.0125 M:

\[\mathrm{pOH=-\log[OH^− ]=-\log 0.0125} \nonumber \]

\[=−(−1.903)=1.903 \nonumber \]

El pH se puede encontrar a partir de\(\ce{pOH}\):

\[\mathrm{pH+pOH=14.00} \nonumber \]

\[\mathrm{pH=14.00−pOH=14.00−1.903=12.10} \nonumber \]

Ejercicio\(\PageIndex{3}\)

La concentración de iones hidronio del vinagre es aproximadamente\(4 \times 10^{−3}\; M\). ¿Cuáles son los valores correspondientes de PoH y pH?

Contestar

PoH = 11.6

pH = 14.00 - PoH = 2.4

La acidez de una solución se evalúa típicamente experimentalmente mediante la medición de su pH. El PoH de una solución no suele medirse, ya que se calcula fácilmente a partir de un valor de pH determinado experimentalmente. El pH de una solución se puede medir directamente usando un medidor de pH (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): (a) Un medidor de pH de grado de investigación utilizado en un laboratorio puede tener una resolución de 0.001 unidades de pH, una precisión de ± 0.002 unidades de pH, y puede costar más de $1000. (b) Un medidor de pH portátil tiene menor resolución (0.01 unidades de pH), menor precisión (± 0.2 unidades de pH) y un precio mucho menor. (crédito b: modificación de obra por Jacopo Werther)

Esta figura contiene dos imágenes. La primera, la imagen a, es de un medidor de p H digital analítico sobre un mostrador de laboratorio. La segunda, la imagen b, es de un medidor digital portátil de p H de mano.

El pH de una solución también puede estimarse visualmente usando indicadores coloreados (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{4}\): (a) Un indicador universal asume un color diferente en soluciones de diferentes valores de pH. Así, se puede agregar a una solución para determinar el pH de la solución. Los ocho viales contienen cada uno un indicador universal y soluciones 0.1-M de ácidos progresivamente más débiles: HCl (pH = l), CH ₃ CO ₂ H (pH = 3), y NH ₄ Cl (pH = 5), agua desionizada, una sustancia neutra (pH = 7); y soluciones 0.1-M de las bases progresivamente más fuertes: KCl (pH = 7), anilina, C ₆ H ₅ NH ₂ (pH = 9), NH ₃ (pH = 11) y NaOH (pH = 13). (b) El papel de pH contiene una mezcla de indicadores que dan diferentes colores en soluciones de diferentes valores de pH. (crédito: modificación de obra por Sahar Atwa).

Esta figura contiene dos imágenes. El primero muestra una variedad de colores de soluciones en vasos de precipitados etiquetados. Una solución roja en un vaso de precipitados se etiqueta como “0.10 M H C l.” Una solución naranja se etiqueta como “0.10 M C H subíndice 3 C O O H.” Una solución amarillo-naranja se etiqueta como “0.1 M N H subíndice 4 C l”. Una solución amarilla se etiqueta como “agua desionizada”. Un segundo vaso de precipitados de solución se etiqueta como “0.10 M K C l.” Una solución verde se etiqueta como “anilina 0.10 M”. Una solución azul se etiqueta como “0.10 M N H subíndice 4 C l (a q)”. Un vaso de precipitados final que contiene una solución azul oscuro se etiqueta como “0.10 M N a O H.” La imagen b muestra papel PhyDrion que se utiliza para medir el pH en el rango de p H de 1 a 12. Se muestra la escala de colores para identificar p H con base en el color junto con varias de las tiras reactivas utilizadas para evaluar p H.

Resumen

La concentración de ion hidronio en una solución de un ácido en agua es mayor que\( 1.0 \times 10^{-7}\; M\) a 25 °C. La concentración de ion hidróxido en una solución de una base en agua es mayor que\( 1.0 \times 10^{-7}\; M\) a 25 °C. La concentración de H ₃ O ⁺ en una solución se puede expresar como el pH del solución;\(\ce{pH} = -\log \ce{H3O+}\). La concentración de OH ⁻ se puede expresar como el pOH de la solución:\(\ce{pOH} = -\log[\ce{OH-}]\). En agua pura, pH = 7.00 y PoH = 7.00

Ecuaciones Clave

• \(\ce{pH}=-\log[\ce{H3O+}]\)
• \(\ce{pOH} = -\log[\ce{OH-}]\)
• [H ₃ O ⁺] = 10 ^−pH
• [OH ⁻] = 10 ^−PoH
• pH + PoH = p K _w = 14.00 a 25 °C

Glosario

ácido

describe una solución en la que [H ₃ O ⁺] > [OH ⁻]

básico

describe una solución en la que [H ₃ O ⁺] < [OH ⁻]

neutral

describe una solución en la que [H ₃ O ⁺] = [OH ⁻]

pH

Medida logarítmica de la concentración de iones hidronio en una solución

PoH

Medida logarítmica de la concentración de iones hidróxido en una solución