17.7: Electrólisis
- Page ID
- 75214
- Describir las celdas electrolíticas y su relación con las celdas galvánicas
- Realizar diversos cálculos relacionados con la electrólisis
En las celdas galvánicas, la energía química se convierte en energía eléctrica. Lo contrario es cierto para las celdas electrolíticas. En las celdas electrolíticas, la energía eléctrica provoca reacciones no espontáneas que ocurran en un proceso conocido como electrólisis. El barttery eléctrico de carga muestra uno de esos procesos. La energía eléctrica se convierte en la energía química en la batería a medida que se carga. Una vez cargada, la batería se puede utilizar para alimentar el automóvil. Los mismos principios están involucrados en las celdas electrolíticas que en las celdas galvánicas. Analizaremos tres celdas electrolíticas y los aspectos cuantitativos de la electrólisis.
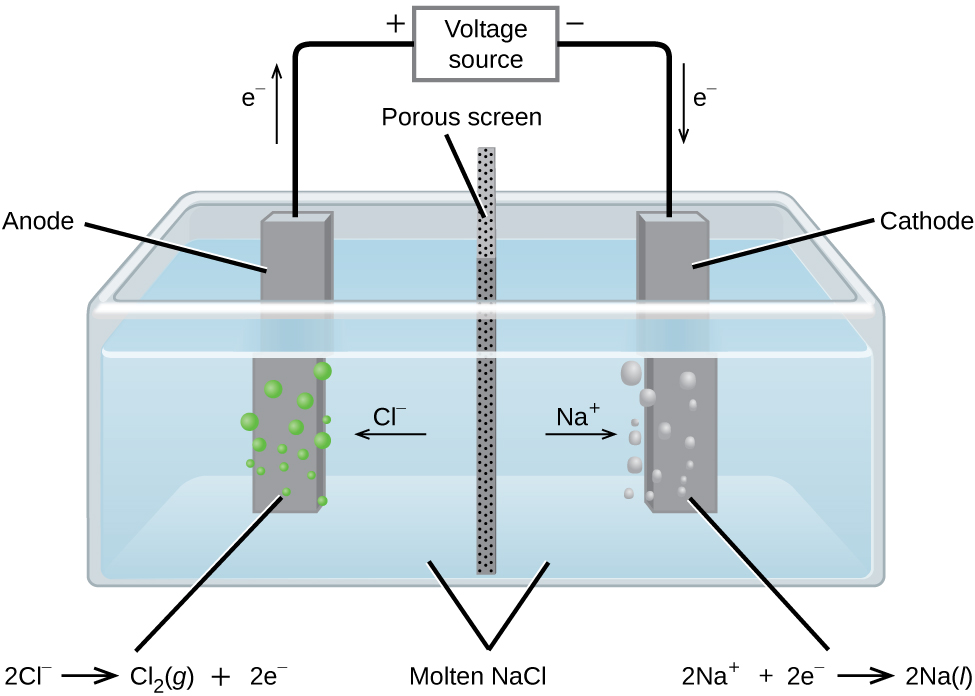
La electrólisis del cloruro de sodio fundido
En el cloruro de sodio fundido, los iones son libres de migrar a los electrodos de una celda electrolítica. En la Figura se muestra un diagrama simplificado de la celda utilizada comercialmente para producir gas sodio metálico y cloro\(\PageIndex{1}\). El sodio es un agente reductor fuerte y el cloro se usa para purificar el agua, y se usa en antisépticos y en la producción de papel. Las reacciones son
\ [\ begin {align}
&\ textrm {ánodo:}\ ce {2Cl-} (l) ⟶\ ce {Cl2} (g) +\ ce {2e-}\ hspace {20px} E^\ circ_ {\ ce {Cl2/Cl-}} =\ mathrm {+1.3\: V}\\
&\ textrm {cátodo:}\ ce {Na+} (l) +\ ce {e-} ⟶\ ce {Na} (l)\ hspace {20px} E^\ circ_ {\ ce {Na+/Na}} =\ mathrm {−2.7\: V}\\\
&\ overline {\ textrm {general :}\ ce {2Na+} (l) +\ ce {2Cl-} (l) ⟶\ ce {2Na} (l) +\ ce {Cl2} (g)\ hspace {20px} E^\ circ_\ ce {celda} =\ mathrm {−4.0\: V}}
\ end {align}\ nonumber\]
La fuente de alimentación (batería) debe suministrar un mínimo de 4 V, pero, en la práctica, los voltajes aplicados suelen ser mayores debido a ineficiencias en el propio proceso.
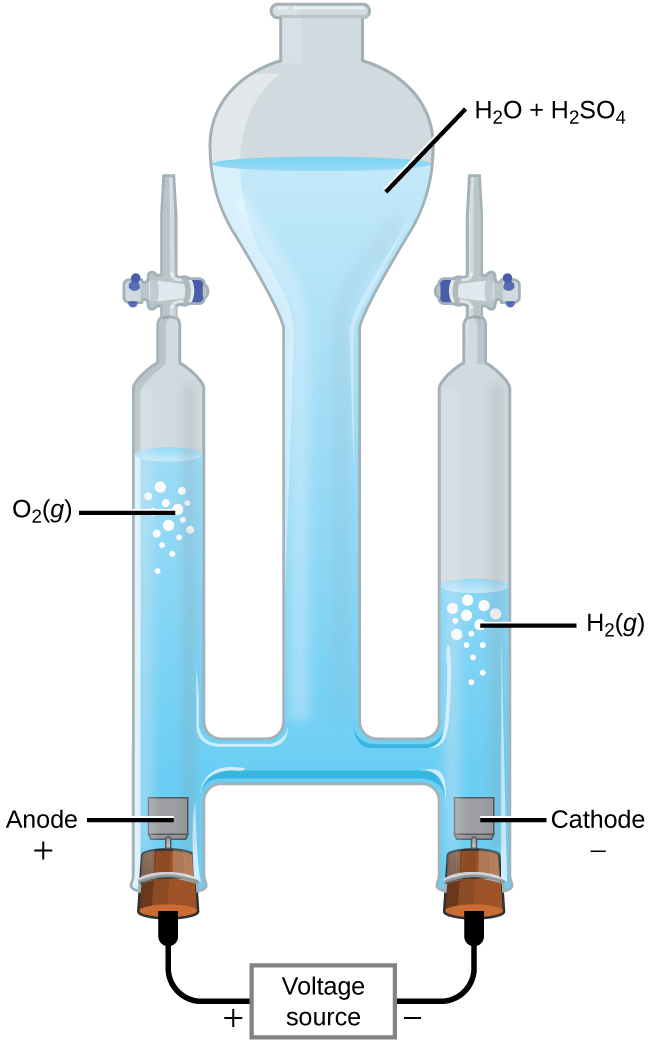
La electrólisis del agua
Es posible dividir el agua en hidrógeno y oxígeno gaseoso por electrólisis. Normalmente se agregan ácidos para aumentar la concentración de ión hidrógeno en solución (Figura\(\PageIndex{2}\)). Las reacciones son
\ [\ begin {align}
&\ textrm {ánodo:}\ ce {2H2O} (l) ⟶\ ce {O2} (g) +\ ce {4H+} (aq) +\ ce {4e-}\ hspace {20px} E^\ circ_\ ce {ánodo} =\ mathrm {+1.229\: V}\\
&\ textrm {cátodo:}\ ce {2H+} (aq) +\ ce {2e-} ⟶\ ce {H2} (g)\ hspace {20px} E^\ circ_\ ce {cátodo} =\ mathrm {0\: V}\\
&\ overline {\ textrm { general:}\ ce {2H2O} (l) ⟶\ ce {2H2} (g) +\ ce {O2} (g)\ hespacio {20px} E^\ circ_\ ce {celda} =\ mathrm {−1.229\: V}}
\ end {align}\ nonumber\]
Tenga en cuenta que el ácido sulfúrico no se consume y que el volumen de gas hidrógeno producido es el doble del volumen de gas oxígeno producido. El voltaje mínimo aplicado es de 1.229 V.
La electrólisis del cloruro de sodio acuoso
La electrólisis del cloruro de sodio acuoso es el ejemplo más común de electrólisis porque más de una especie puede oxidarse y reducirse. Considerando primero el ánodo, las posibles reacciones son
\ [\ begin {align}
&\ textrm {(i)}\ ce {2Cl-} (aq) ⟶\ ce {Cl2} (g) +\ ce {2e-}\ hspace {20px} E^\ circ_\ ce {ánodo} =\ mathrm {+1.35827\: V}\\
&\ textrm {(ii)}\ ce {2H2O} (l) ⟶\ ce {O2} (g) +\ ce {4H+} (aq) +\ ce {4e-}\ hespacio {20px} E^\ circ_\ ce {ánodo} =\ mathrm {+1.229\: V}
\ end {align}\ nonumber\]
Estos valores sugieren que el agua debe oxidarse en el ánodo porque se necesitaría un potencial más pequeño, usando la reacción (ii) para la oxidación daría un potencial celular menos negativo. Cuando se ejecuta el experimento, resulta que en el ánodo se produce cloro, no oxígeno. El proceso inesperado es tan común en la electroquímica que se le ha dado el nombre de sobrepotencial. El sobrepotencial es la diferencia entre el voltaje teórico de la celda y el voltaje real que es necesario para causar electrólisis. Resulta que el sobrepotencial de oxígeno es bastante alto y efectivamente hace que el potencial de reducción sea más positivo. Como resultado, en condiciones normales, el gas cloro es lo que realmente se forma en el ánodo.
Ahora considera el cátodo. Podrían ocurrir tres reducciones:
\ [\ begin {align}
&\ textrm {(iii)}\ ce {2H+} (aq) +\ ce {2e-} ⟶\ ce {H2} (g)\ hspace {20px} E^\ circ_\ ce {cátodo} =\ mathrm {0\: V}\\
&\ textrm {(iv)}\ ce {2H2O} (l) +\ ce {2e-} ⟶\ ce {H2} (g) +\ ce {2OH-} (aq)\ hspace {20px} E^\ circ_\ ce {cátodo} =\ mathrm {−0.8277\ :V}\\\
&\ textrm {(v)}\ ce {Na+ } (aq) +\ ce {e-} ⟶\ ce {Na} (s)\ hspace {20px} E^\ circ_\ ce {cátodo} =\ mathrm {−2.71\: V}
\ end {align}\ nonumber\]
Se descarta la reacción (v) porque tiene un potencial de reducción tan negativo. Bajo condiciones de estado estándar, se preferiría la reacción (iii) a la reacción (iv). Sin embargo, el pH de una solución de cloruro de sodio es de 7, por lo que la concentración de iones hidrógeno es de solo 1× 10 −7 M. A concentraciones tan bajas, la reacción (iii) es poco probable y se produce la reacción (iv). La reacción general es entonces
\[\textrm{overall: }\ce{2H2O}(l)+\ce{2Cl-}(aq)⟶\ce{H2}(g)+\ce{Cl2}(g)+\ce{2OH-}(aq) \hspace{20px} E^\circ_\ce{cell}=\mathrm{−2.186\: V} \nonumber \]
A medida que avanza la reacción, los iones hidróxido reemplazan a los iones cloruro en solución. Así, el hidróxido de sodio se puede obtener evaporando el agua después de que se complete la electrólisis. El hidróxido de sodio es valioso por derecho propio y se usa para cosas como limpiador de horno, abridor de drenaje y en la producción de papel, telas y jabón.
Galvanoplastia
Un uso importante para las celdas electrolíticas es en la galvanoplastia. La galvanoplastia da como resultado un recubrimiento delgado de un metal en la parte superior de una superficie conductora. Las razones para la galvanoplastia incluyen hacer que el objeto sea más resistente a la corrosión, fortalecer la superficie, producir un acabado más atractivo o para purificar el metal. Los metales comúnmente utilizados en galvanoplastia incluyen cadmio, cromo, cobre, oro, níquel, plata y estaño. Los productos de consumo comunes incluyen vajillas chapadas en plata u oro, piezas de automóviles cromadas y joyas. Podemos hacernos una idea de cómo funciona esto investigando cómo se produce la vajilla plateada (Figura\(\PageIndex{3}\)).
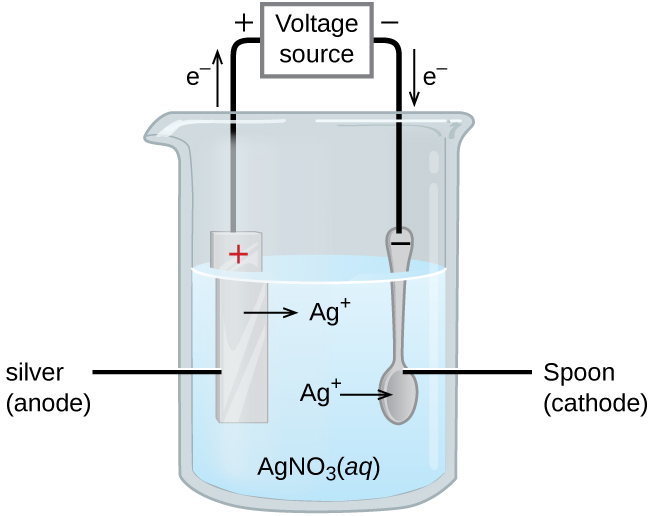
En la figura, el ánodo consiste en un electrodo de plata, mostrado a la izquierda. El cátodo se encuentra a la derecha y es la cuchara, que está hecha de metal económico. Ambos electrodos se sumergen en una solución de nitrato de plata. A medida que aumenta el potencial, fluye la corriente. El metal plateado se pierde en el ánodo a medida que entra en solución.
\[\textrm{anode: }\ce{Ag}(s)⟶\ce{Ag+}(aq)+\ce{e-} \nonumber \]
La masa del cátodo aumenta a medida que los iones de plata de la solución se depositan sobre la cuchara
\[\textrm{cathode: }\ce{Ag+}(aq)+\ce{e-}⟶\ce{Ag}(s) \nonumber \]
El resultado neto es la transferencia de plata metálica del ánodo al cátodo. La calidad del objeto suele estar determinada por el grosor de la plata depositada y la velocidad de deposición.
Aspectos cuantitativos de la electrólisis
La cantidad de corriente que se permite que fluya en una celda electrolítica está relacionada con el número de moles de electrones. El número de moles de electrones se puede relacionar con los reactivos y productos usando estequiometría. Recordemos que la unidad SI para corriente (I) es el amperio (A), que es el equivalente a 1 culombio por segundo (1 A =\(\mathrm{1\: \dfrac{C}{s}}\)). La carga total (Q, en culombios) viene dada por
\[Q=I×t=n×F \nonumber \]
donde
- t es el tiempo en segundos,
- n el número de moles de electrones, y
- F es la constante de Faraday.
Los moles de electrones pueden ser utilizados en problemas estequiométricos. También podría solicitarse el tiempo requerido para depositar una determinada cantidad de metal, como en el segundo de los siguientes ejemplos.
En un proceso utilizado para la galvanoplastia de plata, se pasó una corriente de 10.23 A a través de una celda electrolítica durante exactamente 1 hora. ¿Cuántos moles de electrones pasaron a través de la célula? ¿Qué masa de plata se depositó en el cátodo a partir de la solución de nitrato de plata?
Solución
La constante de Faraday se puede utilizar para convertir la carga (Q) en moles de electrones (n). La carga es la corriente (I) multiplicada por el tiempo
\[n=\dfrac{Q}{F}=\mathrm{\dfrac{\dfrac{10.23\: C}{s}×1\: hr×\dfrac{60\: min}{hr}×\dfrac{60\:s}{min}}{96,485\: C/mol\: e^-}=\dfrac{36,830\: C}{96,485\: C/mol\:e^-}=0.3817\: mol\: e^-} \nonumber \]
Del problema, la solución contiene AgnO 3, por lo que la reacción en el cátodo involucra 1 mol de electrones por cada mol de plata
\[\textrm{cathode: }\ce{Ag+}(aq)+\ce{e-}⟶\ce{Ag}(s) \nonumber \]
La masa atómica de la plata es de 107.9 g/mol, por lo que
\[\mathrm{mass\: Ag=0.3817\: mol\: e^-×\dfrac{1\: mol\: Ag}{1\: mol\: e^-}×\dfrac{107.9\: g\: Ag}{1\: mol\: Ag}=41.19\: g\: Ag} \nonumber \]
Consulta tu respuesta: A partir de la estequiometría, 1 mol de electrones produciría 1 mol de plata. Se involucró menos de medio mol de electrones y se produjo menos de medio mol de plata.
El metal de aluminio puede estar hecho de iones de aluminio por electrólisis. ¿Cuál es la media reacción en el cátodo? ¿Qué masa de aluminio metálico se recuperaría si una corriente de 2.50 × 10 3 A pasara por la solución por 15.0 minutos? Supongamos que el rendimiento es del 100%.
- Responder
-
\(\ce{Al^3+}(aq)+\ce{3e-}⟶\ce{Al}(s)\); 7.77 mol Al = 210.0 g Al.
En una aplicación, se debe depositar una capa de cromo de 0.010 mm sobre una parte con una superficie total de 3.3 m 2 a partir de una solución que contenga iones de cromo (III). ¿Cuánto tiempo tardaría en depositar la capa de cromo si la corriente era de 33.46 A? La densidad del cromo (metal) es de 7.19 g/cm 3.
Solución Este problema trae una serie de temas tratados anteriormente. Un esquema de lo que hay que hacer es:
- Si se puede determinar la carga total, el tiempo requerido es solo el cargo dividido por la corriente
- La carga total se puede obtener a partir de la cantidad de Cr necesaria y la estequiometría
- La cantidad de Cr se puede obtener usando la densidad y el volumen de Cr requerido
- El volumen Cr requerido es el grosor multiplicado por el área
Resolviendo en pasos, y cuidando con las unidades, el volumen de Cr requerido es
\[\mathrm{volume=\left(0.010\: mm×\dfrac{1\: cm}{10\: mm}\right)×\left(3.3\:m^2×\left(\dfrac{10,000\:cm^2}{1\:m^2}\right)\right)=33\: cm^3} \nonumber \]
Se utilizaron centímetros cúbicos porque coinciden con la unidad de volumen utilizada para la densidad. La cantidad de Cr es entonces
\[\mathrm{mass=volume×density=33\cancel{cm^3}×\dfrac{7.19\: g}{\cancel{cm^3}}=237\: g\: Cr} \nonumber \]
\[\mathrm{mol\: Cr=237\: g\: Cr×\dfrac{1\: mol\: Cr}{52.00\: g\: Cr}=4.56\: mol\: Cr} \nonumber \]
Dado que la solución contiene iones cromo (III), se requieren 3 moles de electrones por mol de Cr. El cargo total es entonces
\[Q=\mathrm{4.56\: mol\: Cr×\dfrac{3\:mol\: e^-}{1\: mol\: Cr}×\dfrac{96485\: C}{mol\: e^-}=1.32×10^6\:C} \nonumber \]
El tiempo requerido es entonces
\[t=\dfrac{Q}{I}=\mathrm{\dfrac{1.32×10^6\:C}{33.46\: C/s}=3.95×10^4\:s=11.0\: hr} \nonumber \]
Consulta tu respuesta: En un problema largo como este, un solo cheque probablemente no sea suficiente. Cada uno de los pasos da un número razonable, por lo que las cosas probablemente sean correctas. Presta atención a las conversiones de unidades y a la estequiometría.
¿Qué masa de zinc se requiere para galvanizar la parte superior de una lámina de hierro de 3.00 m × 5.50 m hasta un espesor de 0.100 mm de zinc? Si el zinc proviene de una solución de Zn (NO 3) 2 y la corriente es de 25.5 A, ¿cuánto tiempo tardará en galvanizar la parte superior del hierro? La densidad del zinc es de 7.140 g/cm 3.
- Responder
-
231 g de Zn requirió 23,000 minutos.
Resumen
El uso de la electricidad para forzar que ocurra un proceso no espontáneo es la electrólisis. Las celdas electrolíticas son celdas electroquímicas con potenciales celulares negativos (es decir, una energía libre de Gibbs positiva), y por lo tanto no son espontáneas. La electrólisis puede ocurrir en celdas electrolíticas mediante la introducción de una fuente de alimentación, que suministra la energía para forzar a los electrones a fluir en la dirección no espontánea. La electrólisis se realiza en soluciones, las cuales contienen suficientes iones para que la corriente pueda fluir. Si la solución contiene solo un material, como la electrólisis del cloruro de sodio fundido, es una cuestión sencilla determinar qué se oxida y qué se reduce. En sistemas más complicados, como la electrólisis del cloruro de sodio acuoso, se puede oxidar o reducir más de una especie y se utilizan los potenciales de reducción estándar para determinar la oxidación más probable (la media reacción con el mayor potencial de reducción estándar [más positivo]) y la reducción (la media reacción con el menor potencial de reducción estándar [menos positivo]). A veces se producen medias reacciones inesperadas debido al sobrepotencial. El sobrepotencial es la diferencia entre el potencial teórico de reducción de media reacción y el voltaje real requerido. Cuando está presente, se debe incrementar el potencial aplicado, haciendo posible que se produzca una reacción diferente en la celda electrolítica. La carga total, Q, que pasa por una celda electrolítica puede expresarse como la corriente (I) multiplicada por el tiempo (Q = It) o como los moles de electrones (n) multiplicados por la constante de Faraday (Q = nF). Estas relaciones se pueden utilizar para determinar cosas como la cantidad de material utilizado o generado durante la electrólisis, cuánto tiempo debe continuar la reacción o qué valor de la corriente se requiere.
Resumen
- electrólisis
- proceso que utiliza energía eléctrica para hacer que ocurra un proceso no espontáneo
- celda electrolítica
- celda electroquímica en la que se usa electrólisis; celda electroquímica con potenciales de celda negativos
- galvanoplastia
- depositar una capa delgada de un metal sobre una superficie conductora
- sobrepotencial
- diferencia entre el potencial teórico y el potencial real en una celda electrolítica; el voltaje “extra” requerido para hacer que ocurra alguna reacción electroquímica no espontánea