4.15: RMN en Laboratorio- Composición de Mezclas

Última actualización
Guardar como PDF

Page ID: 79123

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Habrá casos en los que ya se sabe cuál podría ser la estructura. En estos casos:

Debe llamar la atención sobre los datos que apoyan más fuertemente su estructura esperada. Este enfoque demostrará la comprensión evaluativa de los datos; eso significa que puede mirar los datos y decidir qué partes son más cruciales que otras.
También debes llamar la atención sobre los resultados negativos: es decir, picos que podrían estar ahí si este espectro coincidiera con otra, posible estructura, pero que de hecho faltan.

Uno de los problemas más complicados de tratar es el análisis de una mezcla. Esta situación no es infrecuente cuando los estudiantes realizan reacciones en laboratorio y analizan los datos.

A veces los espectros muestran un poco de material de partida mezclado con el producto.
A veces los solventes aparecen en el espectro.
Como cabría esperar, el componente menor suele aparecer como picos más pequeños en el espectro. Si hay menos moléculas presentes, entonces generalmente hay menos protones para absorber en el espectro.
En este caso, probablemente deberías hacer dos conjuntos completamente separados de tablas de datos para tu análisis, una para cada compuesto, o bien una para el compuesto principal y otra para las impurezas.

Recuerde que las proporciones de integración son realmente solo significativas dentro de un solo compuesto. Si tu muestra de RMN contiene algo de benceno (C ₆ _{H 6}) y algo de acetona (CH ₃ _{COCH 3}), y hay un pico a 7.15 que se integra a 1 protón y un pico a 2.10 ppm integrando a 6 protones, podría significar que hay 6 protones en acetona y 1 en benceno, pero puedes decir que eso no es cierto mirando la estructura.

Hay seis protones en el benceno, y todos deberían aparecer cerca de 7 ppm. Hay seis protones en acetona, y todos deberían aparecer cerca de 2 ppm. Si hubiera 1 molécula de benceno por cada molécula de acetona, entonces las integraciones serían iguales.

Suponiendo que la integral pequeña de 1H para el benceno realmente se supone que es 6H, entonces la integral grande de 6H para la acetona también debe representar seis veces más hidrógenos, también. Serían 36 H. Solo hay seis hidrógenos en acetona, por lo que debe representar seis veces más moléculas de acetona que bencenos.

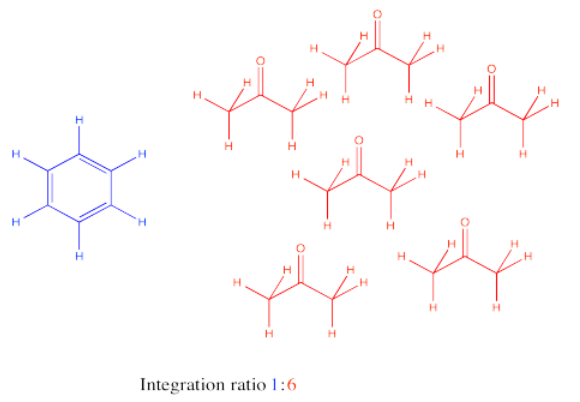
En general, para calcular esa relación, tenemos que tomar la integral que vemos y corregir para el número de hidrógenos que se supone que representa. Si hay seis hidrógenos por molécula, y dividimos la integral por seis, entonces el resultado representa la cantidad relativa de esa molécula en la muestra.

Para benceno: a 7.15 ppm, integral = 1H

Pero 1H/6H por molécula = 0.17 moléculas

Para acetona: a 2.10 ppm, integral = 6H

Pero 6H/6H por molécula = 1 molécula

La relación de acetona a benceno = 1 molécula acetona: 0.17 moléculas benceno = 6 acetona: 1 benceno

A veces un compuesto tendrá varios picos en un espectro de RMN porque tiene varios hidrógenos únicos. Por ejemplo, el acetato de etilo tiene algunos picos diferentes. ¿Y si quisieras comparar la cantidad de acetona con la cantidad de agua?

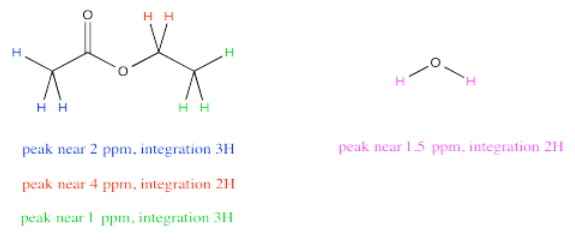
Podría ser tentador medir todas las integrales para los hidrógenos en acetato de etilo y todas las integrales para los hidrógenos en el agua. Al comparar esos dos números te diría la relación entre acetato de etilo y agua, ¿verdad? No exactamente. El acetato de etilo tiene muchos más protones que el agua, así que esa no es una comparación justa. Incluso en una mezcla 1:1 de agua a acetato de etilo, la integral total para el acetato de etilo debe ser mucho mayor que para el agua.

Sin embargo, observe ese pico cerca de 4 ppm en acetato de etilo. Representa 2H, al igual que el pico para el agua. Comparar la integral para el pico a 4 con la integral para el pico a 1.5 proporcionaría una relación bastante buena de acetato de etilo a agua. La razón por la que elegimos la integral a 4 ppm es porque no está cerca de ningún otro pico, por lo que estamos muy seguros de que esta integral representa solo acetato de etilo y nada más.

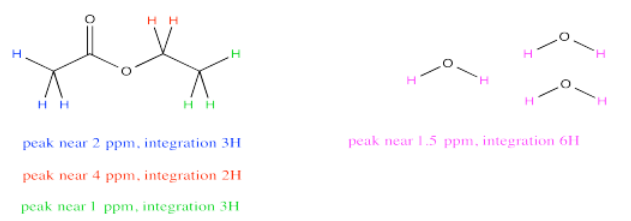
Debido a que ambos picos representan el mismo número de hidrógenos, las integrales dan una relación directa del número de moléculas presentes. Entonces, supongamos que el espectro reporta una integral bruta de 27 para el pico a 1.5 ppm y 9 para el pico a 4 ppm. Recuerde, la integral es solo reportar el área relativa bajo el pico, en lugar de alguna cantidad absoluta, por lo que los números iniciales que obtenemos podrían no sonar como que corresponden a un número razonable de hidrógenos. Es la proporción lo que importa, y la proporción de 27:9 es 3. Si la integral a 1.5 ppm es tres veces mayor que la de 4 ppm, debe haber tres veces más moléculas de agua que las moléculas de acetato de etilo.

Para agua: a 1.5 ppm, integral = 27H

Pero 27H/2H por molécula = 13.5 moléculas

Para acetato de etilo: a 4.2 ppm, integral = 9H

Pero 9H/2H por molécula = 4.5 molécula

La relación de agua a acetato de etilo = 13.5 molécula agua: 4.5 moléculas acetato de etilo = 3 agua: 1 acetato de etilo

A veces hay varios hidrógenos únicos en ambos compuestos que desea comparar, por lo que deberá elegir qué picos comparar. Por ejemplo, tal vez necesite determinar la relación de acetato de etilo a TBME (^terc- butil metil éter, a veces alternativamente llamado MTBE) en una muestra.

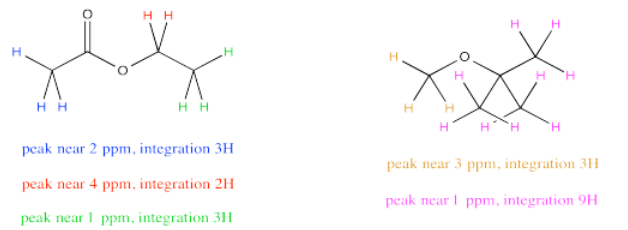
Lo más fácil de hacer puede ser comparar el pico a 2 ppm en acetato de etilo con el pico a 3 ppm en TBME. Se supone que ambos son 3H, por lo que una comparación de esas dos integrales te da una mirada directa a la proporción de moléculas. Por ejemplo, una relación 1:3 entre el pico a 2 ppm y el pico a 3 ppm indicaría una relación 1:3 de moléculas.

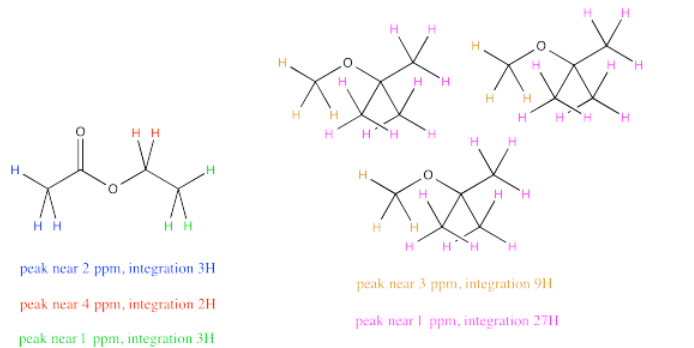
Pero y si, justo antes de hacer tu muestra de RMN, notaste un poco de schmutz en el tubo de RMN y decidieras limpiarlo con algo de acetona. Como resultado, estás bastante seguro de que hay algo de acetona en tu muestra de RMN. Desafortunadamente, eso también aparece a 2 ppm, así que no estás muy seguro de qué parte de la integral a 2 ppm te está diciendo sobre la acetona y qué parte te está diciendo sobre el acetato de etilo.

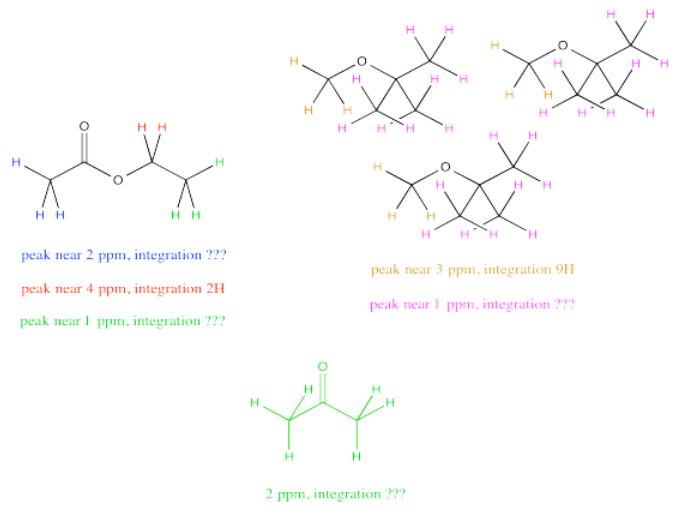
No te preocupes. Todavía se puede recurrir a comparar el pico a 4 ppm en acetato de etilo, que se puede ver muy claramente, con el pico a 3 ppm en TBME, también en el claro. El único problema es que hay que tener en cuenta que un pico representa 2H por molécula y el otro pico representa 3H por molécula. Es necesario ajustar para eso, por ejemplo, multiplicando la integral a 3 ppm por 2/3. Lo estás cortando para poder compararlo con un pico que solo representaría 2H en lugar de 3H. Lo estás poniendo en igualdad de condiciones con el pico del acetato de etilo, para que puedas comparar el número de moléculas presentes, no solo el número de H en cada molécula.

Supongamos que este estudiante mide esas dos integrales en bruto a 4 ppm y 3 ppm, y obtiene valores de 127H y 38H.

Para acetato de etilo: a 4.2 ppm, integral = 127H

Pero 127H/2H por molécula = 63.5 moléculas

Para TBME: a 3.10 ppm, integral = 38H

Pero 38H/3H por molécula = 12.67 molécula

La relación de acetato de etilo a TBME = 63.5 moléculas de acetato de etilo: 12.67 moléculas TBME = 5 acetato de etilo: 1 TBME

En ocasiones, se le puede pedir que exprese la composición de la muestra en términos de composición porcentual más que como proporción. Convertir proporciones a porcentajes implica dividir una parte de la relación por la suma de ambas partes.

% acetato de etilo = acetato\(\frac{5}{5+1} \times 100 \% = 83.3\%\) de etilo

% TBME =\(\frac{1}{5+1} \times 100 \% = 16.7 \%\) TBME

o %TBME =\(100 - 83.3 \% = 16.7 \%\)

Si ha decidido que puede identificar dos conjuntos de picos en el espectro 1H, analizarlos en diferentes tablas facilita mantener el análisis de integración completamente separado también; 1 H en una tabla no será del mismo tamaño integral que 1 H en la otra tabla a menos que las concentraciones de los dos compuestos en la muestra son los mismos.

Sin embargo, comparar la relación de dos integrales para dos compuestos diferentes puede darle la relación de los dos compuestos en solución, así como podríamos determinar la relación de benceno a acetona en la mezcla descrita anteriormente.

Veremos dos ejemplos de mezclas de muestra que podrían surgir en laboratorio. Resultados como estos son eventos bastante comunes en el LABEn el primer ejemplo, un estudiante intentó llevar a cabo la siguiente reacción, una reducción de borohidruro de un aldehído. El borohidruro debe dar un anión hidruro al carbono C=O; el lavado con agua debe entonces suministrar un protón al oxígeno, dando un alcohol.

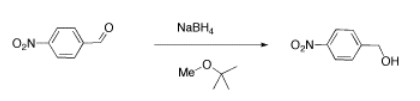
Su reacción produjo el siguiente espectro.

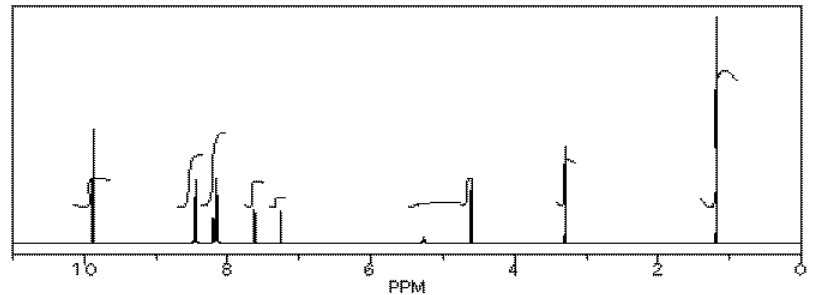
(datos simulados)

A partir de estos datos, produjo la siguiente tabla.

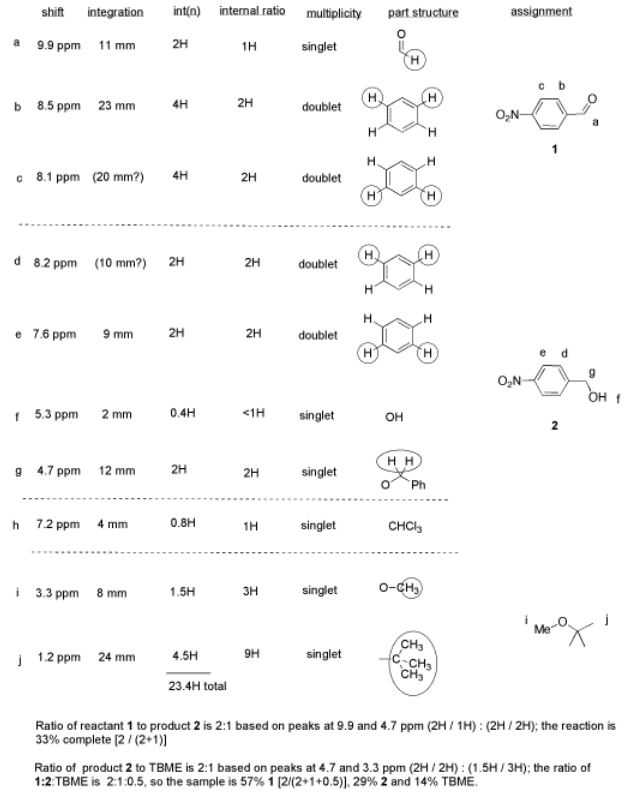
Observe cómo calculó esa proporción. Encontró un pico en la molécula 1, el aldehído, que estaba bastante segura que correspondía al hidrógeno aldehídico, la H unida al C=O; en otras palabras, el CH=O, encontró otro pico de la molécula 2, el alcohol, que estaba bastante segura que representaba los dos hidrógenos en el carbono unido al oxígeno, el CH ₂ -O.

Las integrales para esos dos picos son iguales. Ambos son 2H en su mesa. Sin embargo, señala que dentro de cada molécula, la primera integral representa realmente 1H y la segunda representa 2H. Eso significa que debe haber el doble de molécula 1 que hay molécula 2. De esa manera, habría 2 x CH=O, y su integral sería la misma que la 1 x CH ₂ -O en la otra molécula.

Una forma de abordar este tipo de problemas es:

elija un pico de cada uno de los dos compuestos que desea comparar.
decidir cuántos hidrógenos se supone que representa cada pico en una molécula. ¿Se supone que es un CH2, un CH, un CH3?
dividir el valor integral de ese pico por el número de hidrógenos que se supone que representa en una molécula.
comparar las dos respuestas (integral A/ideal # H) vs (integral B/ideal # H).
la relación de esas dos respuestas es la relación de las dos moléculas en la muestra.

Entonces hay el doble de aldehído que alcohol en la mezcla. Solo en términos de estos dos compuestos, tiene 33% de alcohol y 66% de aldehído. Eso es\(\frac{1}{1+2} \times \%\) para el alcohol, y\(\frac{2}{1+2} \times 100 \%\) (2/ (1+2)) para el aldehído. Ese cálculo solo representa la cantidad de componente individual dividido por el total de los componentes que quiere comparar.

Aquí hay una serie de cosas que tomar nota.

Su reacción realmente no funcionó muy bien. Ella todavía tiene material de partida mayoritario, no producto.
Obtendrá una buena calificación en este laboratorio. Aunque el experimento no funcionó bien, tiene buenos datos, y los ha analizado muy claramente.
Ella ha separado su tabla de datos en diferentes secciones para diferentes compuestos. A veces eso facilita el análisis de las cosas.
Ella ha anotado los datos integrales reales (puede haber medido la integral con una regla) y también los ha convertido en una proporción más conveniente, basada en la integral para un pico del que se sentía segura.
Ella fue un paso más allá, e indicó la relación de integración interna dentro de cada compuesto individual.
Ella calculó el% de finalización de la reacción utilizando los datos integrales para el reactivo y el producto, y dejó en claro qué parte de los datos utilizó para ese cálculo. Un procedimiento similar se podría hacer si un estudiante solo estuviera tratando de separar dos componentes en una mezcla en lugar de llevar a cabo una reacción.
También calculó la pureza general de la mezcla, incluyendo una impureza de disolvente que no logró eliminar.
Sin embargo, el CHCl ₃ no está incluido en su análisis de pureza. CHCl ₃ realmente no es parte de su muestra; solo estaba presente en el solvente de RMN, por lo que no representa nada en el material con el que terminó al final del laboratorio.

Otro alumno realizó una reacción similar, que se muestra a continuación. También terminó la reacción lavando con agua, pero debido a que el metanol es soluble en agua, tuvo que extraer su producto del agua. Eligió usar diclorometano para ese propósito.

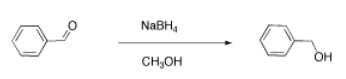
Obtuvo los siguientes datos.

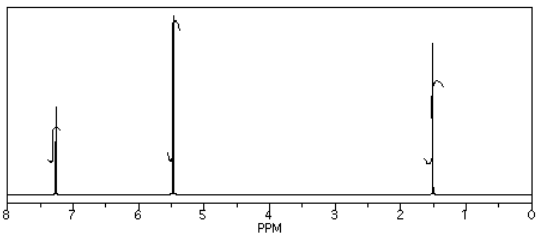
A partir de estos datos, construyó la siguiente tabla.

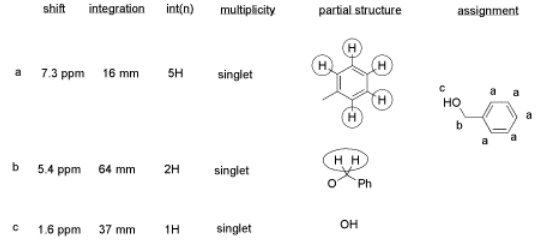
También hay algunas cosas que aprender sobre esta mesa.

¿La relación de integración realmente coincide con los datos integrales? ¿O es esto solo una idea de deseos?
Esta tabla podría reflejar lo que quiere ver en los datos. Pero, ¿qué más podría haber en los datos?
El CHCl ₃ se ve a menudo en los espectros de RMN si se usa CDCl ₃ para la muestra de RMN. Está ahí, a 7.2 ppm.
El “sobrante” o disolvente residual es muy común en los datos reales de laboratorio. Ahí está, CH ₂ Cl ₂ de la extracción, a 5.4 ppm.
¿Qué pasa con el agua? A veces las personas no secan sus soluciones adecuadamente antes de evaporar el solvente. Probablemente hay agua alrededor de 1.5 a 1.6 ppm aquí.

Este alumno podría no obtener una muy buena calificación; la muestra ni siquiera aparece en el espectro, por lo que la perdió en alguna parte. Pero su análisis también es pobre, por lo que realmente obtendrá una calificación terrible.

Ejercicio\(\PageIndex{1}\)

Tres estudiantes realizaron una síntesis de un éster fragante, propanoato de etilo, CH ₃ CH _{2 CO 2} CH ₂ CH ₂ CH ₃. Durante sus reacciones, cada uno utilizó un disolvente diferente. Los estudiantes pudieron ver picos en el espectro de RMN para propanoato de etilo, así como picos para cloroformo (CHCl ₃, en el CDCl ₃ que usaron para hacer sus muestras de RMN).

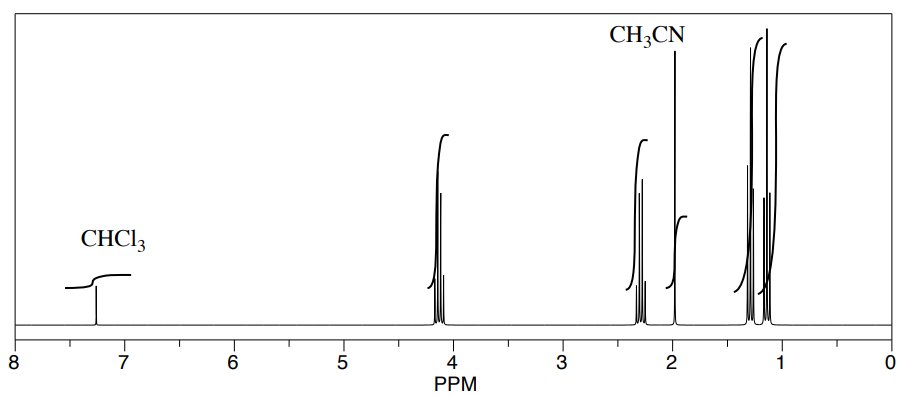
También pudieron determinar que tenían algún solvente sobrante en sus muestras consultando una tabla útil de impurezas solventes en RMN (que encontraron en Goldberg et. al. , Organometálicos 2010, 29, 2176-2179).

¿Cuál es la relación entre el disolvente sobrante y el propanoato de etilo en cada muestra?
¿Cuál es el porcentaje de cada muestra que es solvente sobrante?

Contestar

a) Estudiante 1: Usemos el pico H ₂ C-O de propanoato de etilo a 4 ppm y el acetonitrilo metilo a 2 ppm. La proporción parece ser 2:1, pero representan 2 protones y 3 protones, respectivamente. Eso significa que la relación de moléculas es 2/ 2:1 /3 = 3:1 de propanoato de etilo: acetonitrilo.

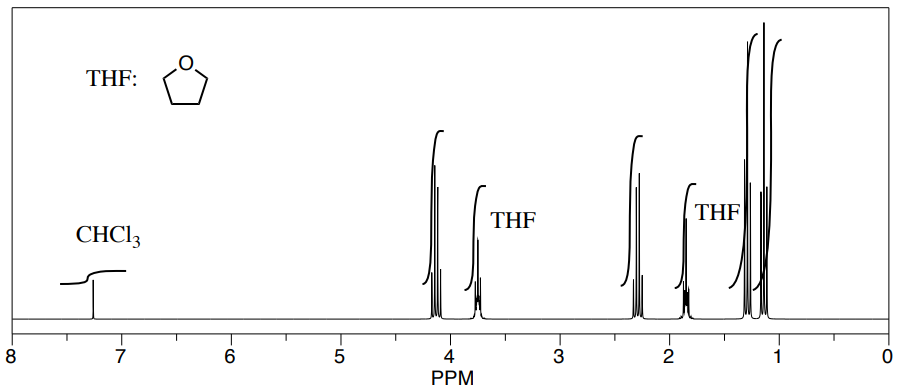
estudiante 2: Utilizaremos el pico H ₂ C-O de propanoato de etilo a 4 ppm y el pico H ₂ C-O de THF a 3.5 ppm. La proporción parece ser 3:2, pero representan 2 protones y 4 protones, respectivamente. Eso significa que la relación de moléculas es 3/ 2:2 /4 = 12:4 = 3:1 propanoato de etilo: THF.

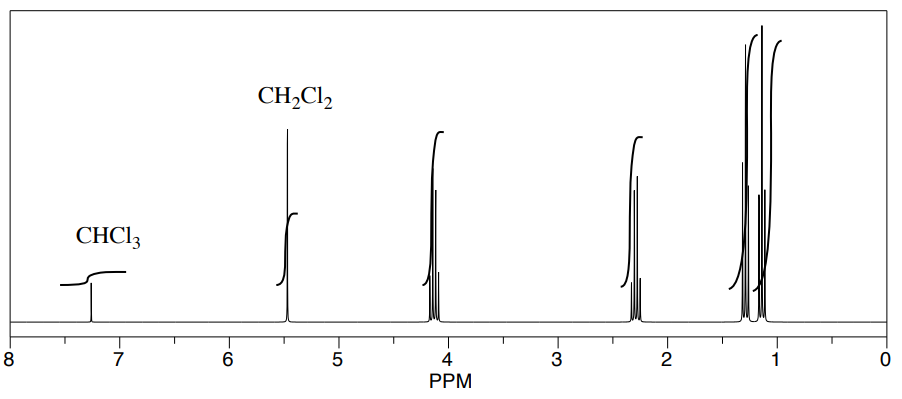
estudiante 3: Observa el pico H ₂ cCl ₂ de diclorometano a 5 ppm y el pico H ₂ C-O de THF a 4 ppm. La relación parece ser 1:2, y ambos representan 2 protones, por lo que la relación de moléculas es 1:2 de diclorometano:propanoato de etilo.

b) Estudiante 1: La muestra es\([\frac{1}{1 + 3}] \times 100 \% = 25%\) acetonitrilo.

estudiante 2: La muestra es\([\frac{1}{1 + 3}] \times 100 \% = 25%\) THF.

estudiante 3: La muestra es\([\frac{1}{1 + 2}] \times 100 \% = 33%\) acetonitrilo.

Ejercicio\(\PageIndex{2}\)

Un estudiante intentó agregar un reactivo de Grignard al benzaldehído.

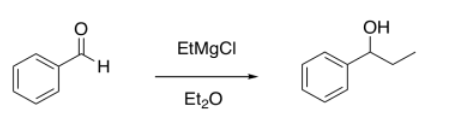
Obtuvo los siguientes datos (bueno, se trata de un espectro simulado). ¿Cuál fue la composición de su producto?

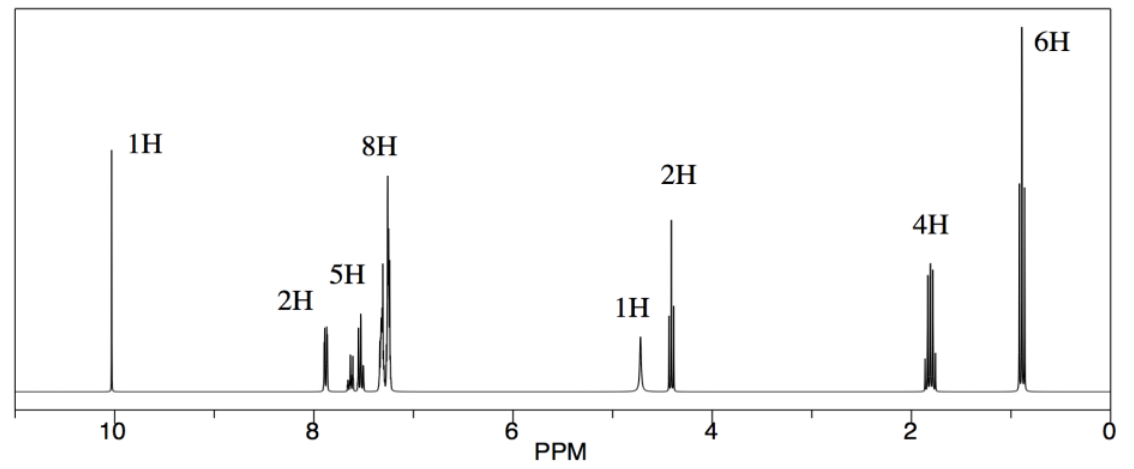
Contestar

Los mangos de RMN obvios son el protón de aldehído H-C=O a 10 ppm para el benzaldehído y el protón H-C-O adyacente al alcohol a 4.5 ppm para 1-fenilpropanol.

Cada uno de esos picos representa un protón, por lo que la relación integral de 1:2 sugiere una relación de bezaldehído a 1-fenilpropanol de 1:2. Eso se traduce en 33% de benzaldehído, 67% de 1-fenilpropanol.

Ejercicio\(\PageIndex{3}\)

Un estudiante intentó ejecutar una oxidación de Swern en alcohol bencílico.

Obtuvo los siguientes datos (espectro simulado). ¿Cuál fue la composición de su producto?

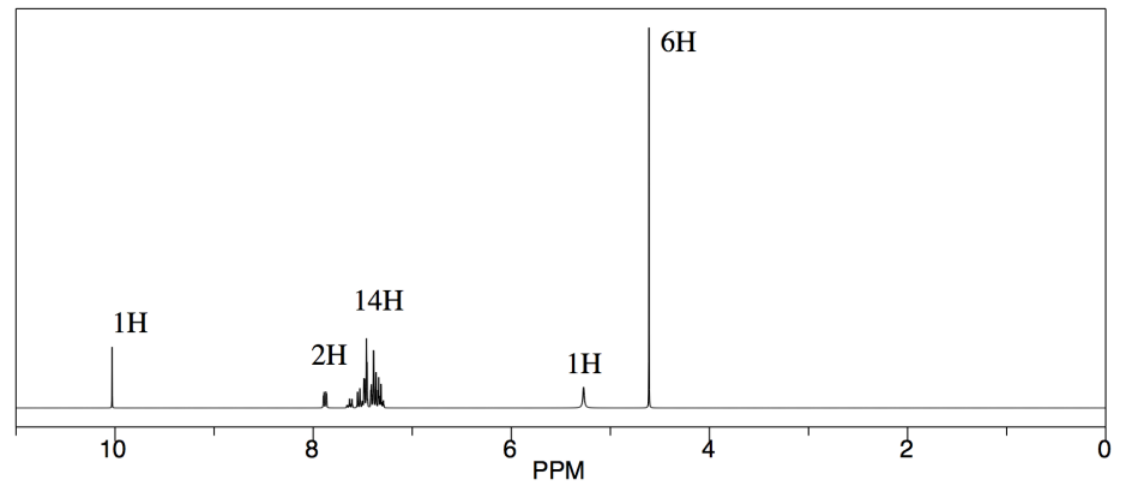
Contestar

Los mangos de RMN aquí son el protón de aldehído H-C=O a 10 ppm para el benzaldehído y los protones H ₂ C-O adyacentes al alcohol cerca de 5 ppm para el alcohol bencílico.

En este caso, necesitamos corregir los diferentes números de protones representados por cada pico: 1H para el pico de aldehído pero 2H para el de alcohol. Por lo tanto, la relación integral de 1:6 sugiere una relación de bezaldehído a 1-fenilpropanol de 1:3. Eso se traduce en 25% benzaldehído, 75% 1-fenilpropanol.

Ejercicio\(\PageIndex{4}\)

Un estudiante intentó realizar una polimerización de trans-esterificación con apertura de anillo.

Obtuvo los siguientes datos (espectro simulado). Ella sabe que el alcohol debe actuar como el nucleófilo inicial y debe encontrarse al final de la cadena polimérica. ¿Cuál es el grado de polimerización (es decir, el número de unidades repetitivas en la cadena)?

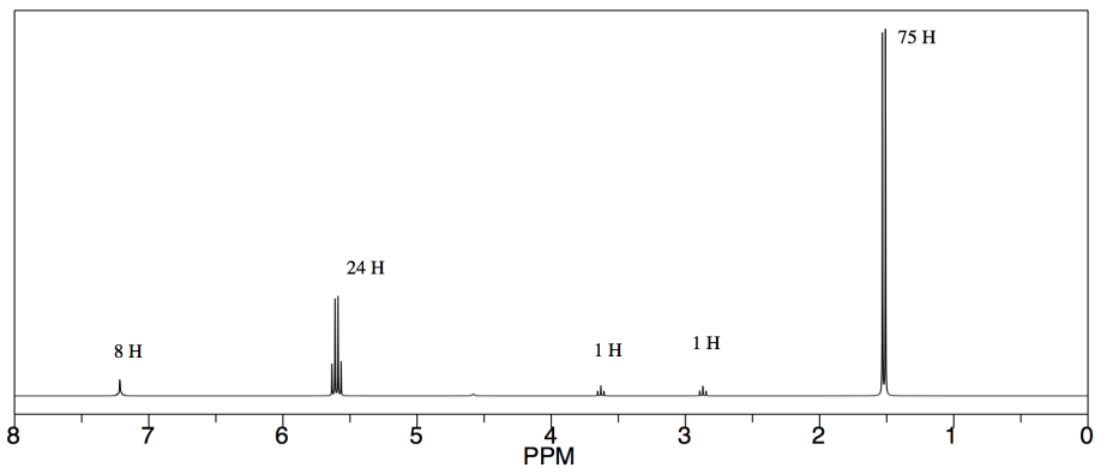
Contestar: Podríamos usar el pico correspondiente al protón O-CH-C=O por encima de 5 ppm para la unidad de repetición y el pico para el protón CH _2-O en el grupo iniciador/final cerca de 3.5 ppm. La relación integral es de 24:1, pero representan diferentes números de hidrógenos, por lo que la relación de unidad repetida a grupo final es realmente 24/ 1:1 /2, o 48:1. El grado de polimerización es 48.