1.4: Cifras significativas

Las cifras significativas están relacionadas con los errores asociados con los números medidos. Es importante entender las cifras significativas porque cuando los cálculos se hacen usando números con errores, la respuesta no puede tener menos error que el error en cualquier número original. La respuesta necesita corrección para las cifras significativas.

Precisión y precisión

Los números medidos tienen dos tipos de errores, sistemáticos y aleatorios, que determinan la exactitud y precisión del número medido, como se ilustra en la Fig. 1.4.1.

Figura\(\PageIndex{1}\): Representación de alta precisión con menor precisión (izquierda) y baja precisión con alta precisión (derecha). Fuente: DarkeVil/Dominio público

Errores sistemáticos

Los errores sistemáticos son constantes, es decir, tienen el mismo valor en cada medición. Por ejemplo, la varilla del medidor es un poco corta o un poco larga que un metro, introducirá un error sistemático. Los errores sistemáticos suelen ocurrir debido a una calibración inexacta del instrumento de medición. Los errores sistemáticos determinan en qué medida difiere el valor medido del valor real.

Errores aleatorios

Los errores aleatorios son la variabilidad estadística del número medido. Los errores aleatorios varían de una observación a otra. Los errores aleatorios se cancelan si se toman muchas medidas y se promedian. Las mediciones científicas generalmente se toman al menos por triplicado y se promedian para minimizar los errores aleatorios. Los errores aleatorios determinan qué tan cerca están los números medidos repetidos entre sí.

Precisión

La precisión o veracidad de la medición se define como lo cerca que está el valor promedio del valor real.

Cuanto más cerca esté el promedio del valor real, más exacto o verdadero es, como se ilustra en la Fig. 1.4.1. La veracidad depende de errores sistemáticos, es decir, errores menos sistemáticos, más precisos el promedio.

Precisión

La precisión se define como lo cerca que están las mediciones individuales entre sí.

Cuanto más cerca estén los valores individuales entre sí, más precisa será la medición, independientemente de si es exacta o no, como se ilustra en la Fig. 1.4.1. La precisión depende de errores aleatorios, es decir, errores aleatorios más sustanciales significan menos precisión.

Número exacto e inexacto

Hay dos tipos de números, contar números que son exactos y números medidos que son inexactos.

Si el valor es un número contado, es un número exacto.

Es decir, no hay error en ello. Por ejemplo, una compra de una docena de naranjas contiene exactamente 12 nos de naranjas; no puede ser 11.5 o 12.5.

Números inexactos y rango de error

Cuando se mide un valor, viene con un error de medición.

Un número medido con un error se llama número inexacto.

Por ejemplo, cuando la misma docena de naranjas se compran en masa, la balanza puede leerla 1572.6 g, o 1573 g, o 1570 g, dependiendo de si el dígito más pequeño que muestra la balanza es 0.1g, 1 g, o 10 g. Supongamos que el saldo es exacto a 1 g y reporta la masa 1573 g; la masa real puede estar en cualquier lugar en el rango de 1572.5g-a-1573.4g. El dígito medido más pequeño, es decir, el número en el lugar de uno, en este caso, es un número estimado asociado a un error. Por convención, el dígito estimado tiene ±1 errores asociados a él. Por ejemplo, los números medidos antes mencionados se reportan en la ciencia como 1572. 6 g ± 0.1 g, 157 3 g ± 1 g, o 15 7 0 g ± 10 g, respectivamente. Los dígitos estimados se muestran en negrita en los ejemplos.

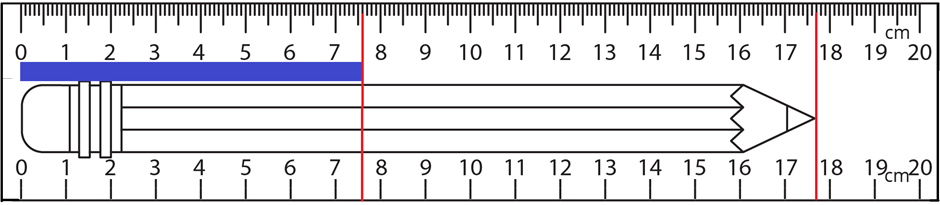
El dígito más pequeño en la pantalla de los instrumentos digitales es un número estimado. En la medición utilizando instrumentos que no tienen pantalla digital, se suma al valor reportado el dígito más pequeño marcado en el instrumento más un dígito menor que el dígito mínimo marcado. El dígito más pequeño reportado es un dígito estimado. Por ejemplo, la longitud del lápiz en la Fig 1.4.2 se reporta como 17. 7 cm usando la regla en la parte inferior, donde 17 incluye el dígito más pequeño marcado en la regla, y el último dígito, es decir, 0.7 es un dígito estimado. Por convención, el rango de error en este valor se muestra como 17. 7 ± 0.1. La misma longitud es de 17.7 0 cm usando la regla en la parte superior en la Fig. 1.4.2l, donde 17.7 incluye el dígito más pequeño marcado en la regla, y el último dígito reportado, es decir, 0, es un dígito estimado. Por convención, el rango de error en este valor se muestra como 17.7 0 ± 0.01. Los dígitos estimados están marcados en negrita.

Figura\(\PageIndex{1}\): Ilustración de mediciones que producen números inexactos. La longitud de un rectángulo azul es de 7.6 0 ± 0.01 cm mediante el uso de una regla más precisa en la parte superior y 7. 6 ±0.1 cm mediante el uso de una regla menos precisa en la parte inferior. El dígito estimado está marcado en negrita.

Reglas para determinar las cifras significativas en números medidos

Cifras significativas

Todos los dígitos reportados en el valor medido, incluyendo el dígito estimado, son cifras significativas (SF).

Por ejemplo, 1572.6 g, 1573 g y 1570 g tienen cifras significativas de 5, 4 y 3, respectivamente.

Precaución

Tenga en cuenta que cero en la última lectura 1570g no es significativo; es un cero marcador de posición que se necesita para colocar el dígito estimado 7 en el lugar de las decenas.

Es crucial encontrar cifras significativas en los números medidos porque, cuando se utilizan en los cálculos, la respuesta no puede tener menos error que el error máximo en cualquier número medido utilizado en el cálculo. Las reglas para determinar los números significativos en un número medido son las siguientes.

1. Todos los dígitos distintos de cero son significativos, por ejemplo, 1572 tiene 4 SF. Los ceros pueden o no ser significativos. En los siguientes ejemplos, los ceros en negrita no son significativos.
2. Los ceros entre dígitos distintos de cero son significativos, por ejemplo, 1305.6 tiene 5 SFs.
3. Los ceros a la izquierda no son significativos, por ejemplo, 0.0 134 tiene 3 SFs.
4. Los ceros finales no son significativos si no hay un punto decimal presente, por ejemplo, 157 0 tiene 3 SFs. Los ceros finales son significativos si el punto decimal está presente, por ejemplo, 1570. tiene 4 SFs porque el punto decimal está presente. De igual manera, 0.0 124 tiene 3 SFs, pero 0.0 1240 tiene 4 SFs porque el punto decimal está presente.
5. La confusión surge cuando hay más de un ceros al final y el punto decimal está ausente. Por ejemplo, 1500 g tiene 2 SF por convención, pero si el saldo fue exacto a 10 g, uno de los cero era un dígito estimado y fue significativo. Convertir el número a una notación científica resuelve este problema. La parte del coeficiente de la notación científica muestra todas las cifras significativas en la medición. Por ejemplo, el número 1500 g, si se muestra en notación científica como 1.5 x 10 ³ tiene 2 SFs, pero el mismo número mostrado como 1.50 x 10 ³ tiene 3 SFs.

Redondeo de la respuesta calculada con números inexactos

Cuando se utilizan números inexactos en los cálculos, la respuesta debe redondearse a un número apropiado de cifras significativas, determinado por las siguientes reglas.

Reglas de redondeo

1. Un número se redondea manteniendo los dígitos más grandes iguales a cifras significativas y dejando o reemplazando los dígitos menores restantes con ceros de marcador de posición. Los ceros de marcador de posición están en negrita en los siguientes ejemplos. Por ejemplo, 13543 se convierte en 135 00 cuando se redondea a tres significativos.
2. Si el dígito más grande caído es 4 o menos de 4, simplemente se cae. Por ejemplo, 23145 se convierte en 231 00, cuando se redondea a tres cifras significativas.
3. Si el dígito más grande caído es 5 o más de 5, entonces el dígito más pequeño retenido se incrementa en uno. Por ejemplo, 13543 se convierte en 14 000 cuando se redondea en dos cifras significativas.

Reglas para determinar las cifras significativas en una respuesta calculada

En las siguientes reglas, el seguimiento de figuras significativas que dictan las cifras significativas en la respuesta se mantiene mediante el uso de fuentes en negrita.

1. Además y resta, la respuesta tiene el mismo número de decimales que el número con el menor número de decimales en los números originales. Por ejemplo, 13. 2 + 12.252 = 25. 4 52 se redondea a 25. 5 para mantener una posición decimal.
2. En multiplicación y división, la respuesta tiene el mismo número de cifras significativas que el número original con el menor número de cifras significativas. Por ejemplo, 1.35 x 2.1 = 2.8 35 se redondea a 2.8.

Nota

Si las operaciones matemáticas se realizan en una serie de pasos, realice un seguimiento de las cifras significativas pero no redondee las respuestas intermedias. Lleve tantos dígitos como sea posible desde las respuestas intermedias hasta el siguiente paso de cálculo. Redondear la respuesta final siguiendo las reglas anteriores. Por ejemplo, (13. 2 + 12.252) x (1.35 x 2.1) = 25.4 52 x 2.8 35 = 72 .15642 es redondo a 72 de acuerdo con 2.8 35 que debería haberse redondeado a 2.8 en un cálculo de un solo paso. Redondear las respuestas intermedias conducirá a una respuesta final incorrecta de 71 en lugar de 72 más correcta, es decir (13.2 + 12.252) x (1.35 x 2.1) = 25.5 x 2.8 = 71

Precaución

Los números exactos tienen un número ilimitado de cifras significativas, lo que significa que no restringen las cifras significativas en la respuesta calculada.

Ejemplo\(\PageIndex{1}\)

Si 12 naranjas pesan 1572.6 g calcular la masa de 1 naranja en gramos?

Solución

\ begin {ecuación}
1572.6\ mathrm {~g}/12=131.05\ mathrm {~g}\ nonumber
\ end {ecuación}

Explicación: La respuesta tiene 5 SFs porque 12 es un número contado y exacto. El único número inexacto en el cálculo que dicta las cifras significativas en la solución es 1572.6, que tiene 5 SFs.

Ejemplo\(\PageIndex{2}\)

Se vendieron 11 veces una docena de naranjas. ¿Calcular el total de naranjas vendidas?

Solución

\ begin {ecuación}
12\ times 11=132\ text {naranjas}\ nonumber
\ end {ecuación}

Explicación: La respuesta no es redondeada porque ambos números en el cálculo son exactos, por lo que la respuesta también es exacta con cifras significativas ilimitadas.