25.3: Voltametría de Barrido Lineal

En el experimento voltamétrico más simple aplicamos una rampa de potencial lineal como señal de excitación y registramos la corriente que fluye en respuesta al cambio de potencial. Entre las variables experimentales bajo nuestro control se encuentran el potencial inicial, el potencial final, la velocidad de barrido y si elegimos agitar la solución o dejarla sin remover. A esto le llamamos voltamperometría de barrido lineal.

Para ilustrar cómo funciona la voltametría de barrido lineal, consideremos qué sucede cuando reducimos\(\text{Fe(CN)}_6^{3-}\) a\(\text{Fe(CN)}_6^{4-}\) en el electrodo de trabajo. La relación entre las concentraciones de\(\text{Fe(CN)}_6^{3-}\), la concentración y el potencial viene dada por la ecuación de Nernst\(\text{Fe(CN)}_6^{4-}\)

\[E=+0.356 \text{ V}-0.05916 \log \frac{\left[\mathrm{Fe}(\mathrm{CN})_{6}^{4-}\right]_{x=0}}{\left[\mathrm{Fe}(\mathrm{CN})_{6}^{3-}\right]_{x=0}} \label{lsv1} \]

donde +0.356V es el potencial de estado estándar para el par\(\text{Fe(CN)}_6^{3-}\)/\(\text{Fe(CN)}_6^{4-}\)redox, y x = 0 indica que las concentraciones de\(\text{Fe(CN)}_6^{3-}\) y\(\text{Fe(CN)}_6^{4-}\) son aquellas en la superficie del electrodo de trabajo. Utilizamos concentraciones superficiales en lugar de concentraciones a granel porque la posición de equilibrio para la reacción redox

\[\mathrm{Fe}(\mathrm{CN})_{6}^{3-}(a q)+e^{-}\rightleftharpoons\mathrm{Fe}(\mathrm{CN})_{6}^{4-}(a q) \label{lsv2} \]

se establece en la superficie del electrodo.

Supongamos que tenemos una solución para la cual la concentración inicial de\(\text{Fe(CN)}_6^{3-}\) es 1.0 mM y que\(\text{Fe(CN)}_6^{4-}\) está ausente. La figura\(\PageIndex{1}\) muestra la relación entre el potencial aplicado y las especies que son estables en la superficie del electrodo.

Figura\(\PageIndex{1}\). Diagrama de potencial para la semi-reacción\(\text{Fe(CN)}_6^{3-}\)/\(\text{Fe(CN)}_6^{4-}\)redox que muestra los potenciales dónde\(\text{Fe(CN)}_6^{3-}\) y dónde\(\text{Fe(CN)}_6^{4-}\) están las especies dominantes. A un potencial de +0.30 V, solo\(\text{Fe(CN)}_6^{3-}\) es estable en la superficie del electrodo.

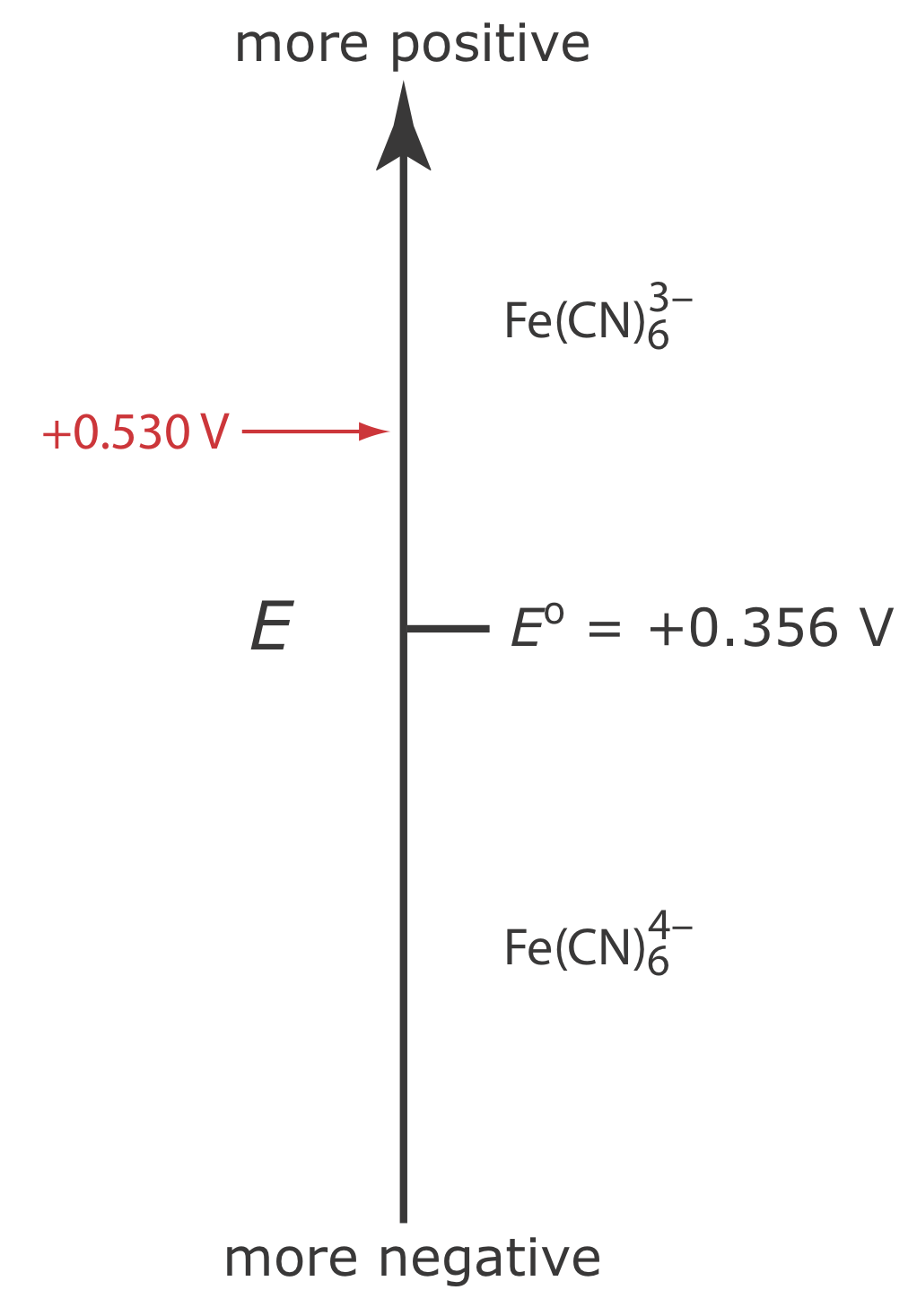
Si aplicamos un potencial de +0.530 V al electrodo de trabajo, las concentraciones de\(\text{Fe(CN)}_6^{3-}\) y\(\text{Fe(CN)}_6^{4-}\) en la superficie del electrodo no se ven afectadas, y no se observa corriente faradaica. Si cambiamos el potencial a +0.356 V parte del\(\text{Fe(CN)}_6^{3-}\) en la superficie del electrodo se reduce\(\text{Fe(CN)}_6^{4-}\) hasta llegar a una condición en la que

\[\left[\mathrm{Fe}(\mathrm{CN})_{6}^{3-}\right]_{x=0}=\left[\mathrm{Fe}(\mathrm{CN})_{6}^{4-}\right]_{x=0}=0.50 \text{ mM} \label{lsv3} \]

Si esto es todo lo que sucede después de aplicar el potencial, entonces habría una breve oleada de corriente faradaica que rápidamente vuelve a cero, que no es el resultado más interesante (aunque esta es la base de la cronoamperometría, un método electroquímico que no consideraremos en este texto). Aunque las concentraciones de\(\text{Fe(CN)}_6^{3-}\) y\(\text{Fe(CN)}_6^{4-}\) en la superficie del electrodo son 0.50 mM, sus concentraciones en solución a granel permanecen sin cambios.

Debido a esta diferencia de concentración, existe un gradiente de concentración entre la superficie del electrodo y la solución a granel. Este gradiente de concentración crea una fuerza impulsora que\(\text{Fe(CN)}_6^{4-}\) se aleja del electrodo y que se transporta\(\text{Fe(CN)}_6^{3-}\) al electrodo (Figura\(\PageIndex{2}\)). A medida que el\(\text{Fe(CN)}_6^{3-}\) llega al electrodo, también, se reduce a\(\text{Fe(CN)}_6^{4-}\). Una corriente faradaica continúa fluyendo hasta que no hay diferencia entre las concentraciones de\(\text{Fe(CN)}_6^{3-}\) y\(\text{Fe(CN)}_6^{4-}\) en el electrodo y sus concentraciones en solución a granel (¡aunque esto podría llevar mucho tiempo!).

Figura\(\PageIndex{2}\). Diagrama esquemático que muestra el transporte de\(\text{Fe(CN)}_6^{4-}\) lejos de la superficie del electrodo y el transporte de\(\text{Fe(CN)}_6^{3-}\) hacia la superficie del electrodo después de la reducción de\(\text{Fe(CN)}_6^{3-}\) a\(\text{Fe(CN)}_6^{4-}\).

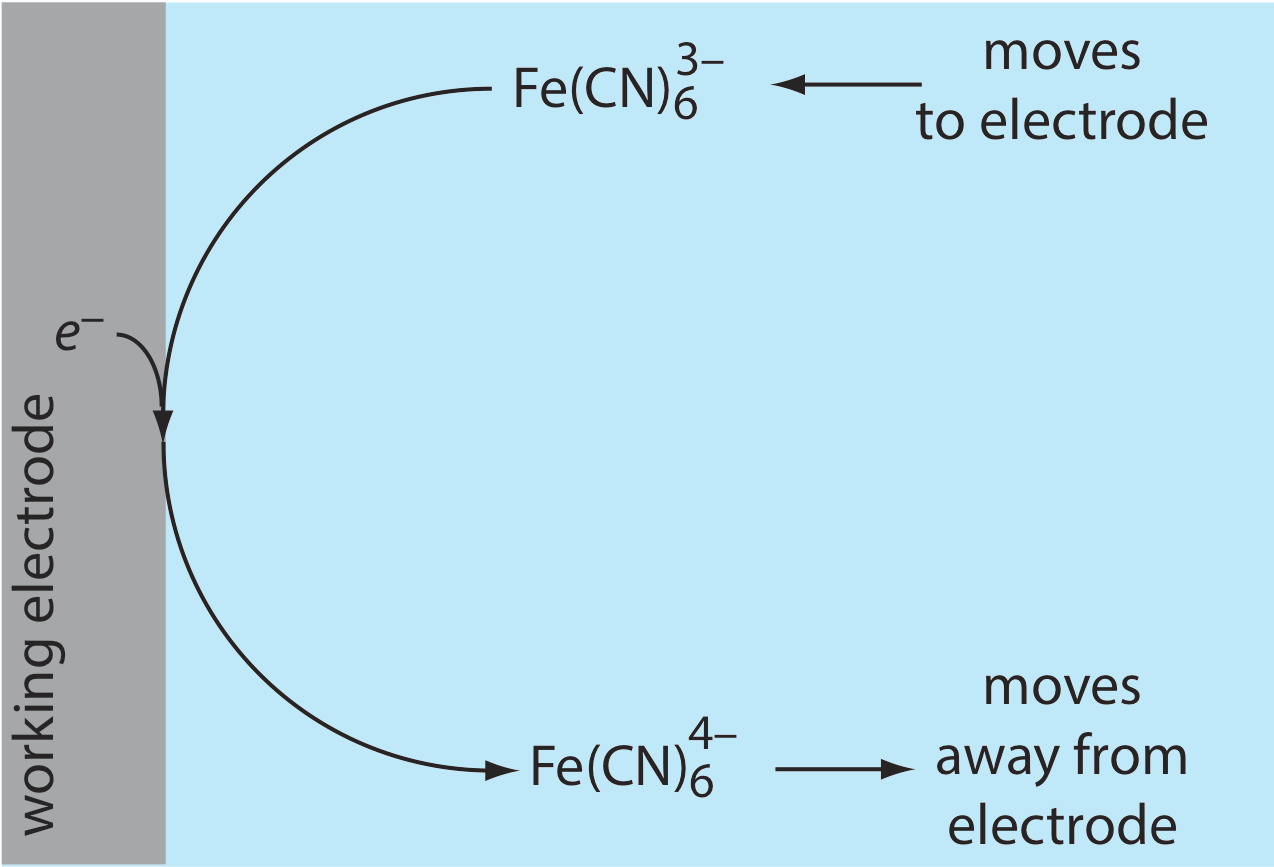
Aunque el potencial en el electrodo de trabajo determina si fluye una corriente faradaica, la magnitud de la corriente está determinada por la velocidad de la reacción de oxidación o reducción resultante. Dos factores contribuyen a la velocidad de la reacción electroquímica: la velocidad a la que los reactivos y productos son transportados hacia y desde el electrodo, lo que llamamos transporte de masa, y la velocidad a la que los electrones pasan entre el electrodo y los reactivos y productos en solución.

Perfiles de concentración en el electrodo de trabajo

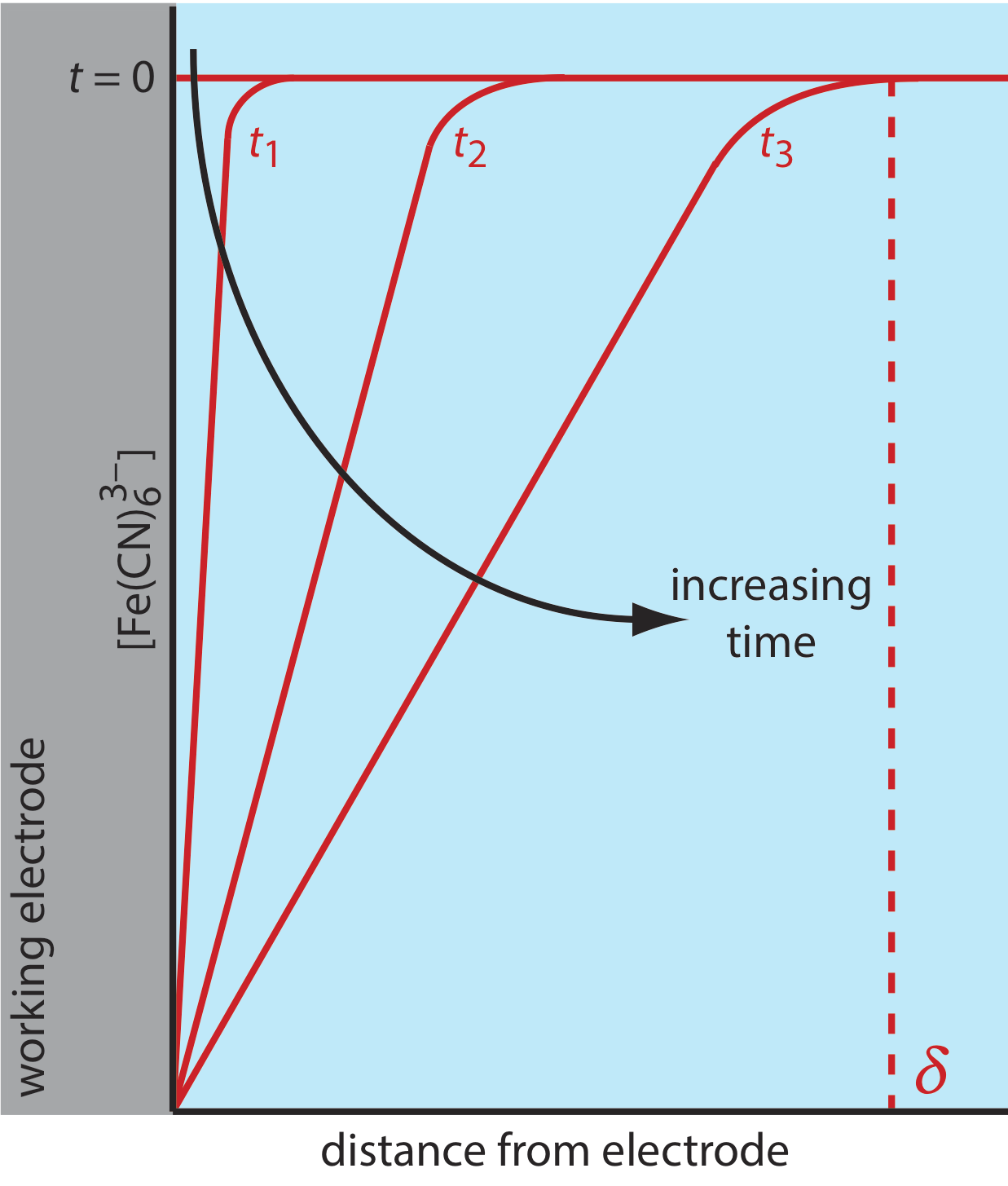
Hay tres modos de transporte de masa que afectan la velocidad a la que los reactivos y productos se mueven hacia o lejos de la superficie del electrodo: difusión, migración y convección. La difusión ocurre siempre que la concentración de un ion o una molécula en la superficie del electrodo es diferente de la de la solución a granel. Si aplicamos un potencial suficiente para reducir completamente\(\text{Fe(CN)}_6^{3-}\) en la superficie del electrodo, el resultado es un gradiente de concentración similar al mostrado en la Figura\(\PageIndex{3}\). La región de solución sobre la que se produce la difusión es la capa de difusión. A falta de otros modos de transporte masivo, el ancho de la capa de difusión,\(\delta\), aumenta con el tiempo ya que el\(\text{Fe(CN)}_6^{3-}\) mosto se difunde desde una distancia cada vez mayor.

Figura\(\PageIndex{3}\). Gradientes de concentración (en rojo) para\(\text{Fe(CN)}_6^{3-}\) seguir la aplicación de un potencial que lo reduce completamente a\(\text{Fe(CN)}_6^{4-}\). Antes de aplicar el potencial (t = 0) la concentración de\(\text{Fe(CN)}_6^{3-}\) es la misma en todas las distancias de la superficie del electrodo. Después de aplicar el potencial, su concentración en la superficie del electrodo disminuye a cero y se\(\text{Fe(CN)}_6^{3-}\) difunde al electrodo desde la solución a granel. Cuanto más tiempo apliquemos el potencial, mayor será la distancia sobre la cual se produce la difusión. La línea roja discontinua muestra la extensión de la capa de difusión en el tiempo t ₃. Estos perfiles asumen que la convección y migración no contribuyen significativamente al transporte masivo de\(\text{Fe(CN)}_6^{3-}\).

La convección ocurre cuando mezclamos la solución, que lleva los reactivos hacia el electrodo y elimina los productos del electrodo. La forma más común de convección es agitar la solución con una barra agitadora; otros métodos incluyen rotar el electrodo e incorporar el electrodo a una celda de flujo.

El modo final de transporte de masa es la migración, que ocurre cuando una partícula cargada en solución es atraída o repelida de un electrodo que porta una carga superficial. Si el electrodo lleva una carga positiva, por ejemplo, un anión se moverá hacia el electrodo y un catión se moverá hacia la solución a granel. A diferencia de la difusión y convección, la migración afecta únicamente al transporte masivo de partículas cargadas.

El movimiento del material hacia y desde la superficie del electrodo es una función compleja de los tres modos de transporte de masa. En el límite donde la difusión es la única forma significativa de transporte de masa, la corriente\(i\), en una celda voltamétrica es proporcional a la pendiente del perfil de concentración en la Figura\(\PageIndex{3}\)

\[i \propto \frac {\partial C} {\partial x} \label{lsv4} \]

donde\(C\) está la concentración de\(\text{Fe(CN)}_6^{3-}\) y\(x\) es la distancia.

Para que la Ecuación\ ref {lsv4} sea válida, la convección y la migración no deben interferir con la formación de una capa de difusión. Podemos eliminar la migración agregando una alta concentración de un electrolito de soporte inerte. Debido a que los iones de carga similar son igualmente atraídos o repelidos desde la superficie del electrodo, cada uno tiene la misma probabilidad de sufrir migración. Un gran exceso de electrolito inerte asegura que pocos reactivos o productos experimenten migración. Si bien es fácil eliminar la convección al no agitar la solución, existen diseños experimentales donde no podemos evitar la convección, ya sea porque debemos agitar la solución o porque estamos usando una celda de flujo electroquímica. Afortunadamente, como se muestra en la Figura\(\PageIndex{4}\), la dinámica de un fluido que se mueve más allá de un electrodo da como resultado una pequeña capa de difusión, típicamente de 1 a 10 μm de grosor, en la que la tasa de transporte de masa por convección cae a cero.

Figura\(\PageIndex{4}\). Gradiente de concentración para\(\text{Fe(CN)}_6^{3-}\) cuando se agita la solución. La difusión es la única forma significativa de transporte de masa cerca de la superficie del electrodo. A distancias mayores que\(\delta\), la convección es la única forma significativa de transporte de masa, manteniendo una solución homogénea en la que la concentración de\(\text{Fe(CN)}_6^{3-}\) at\(\delta\) es la misma que su concentración en solución a granel.

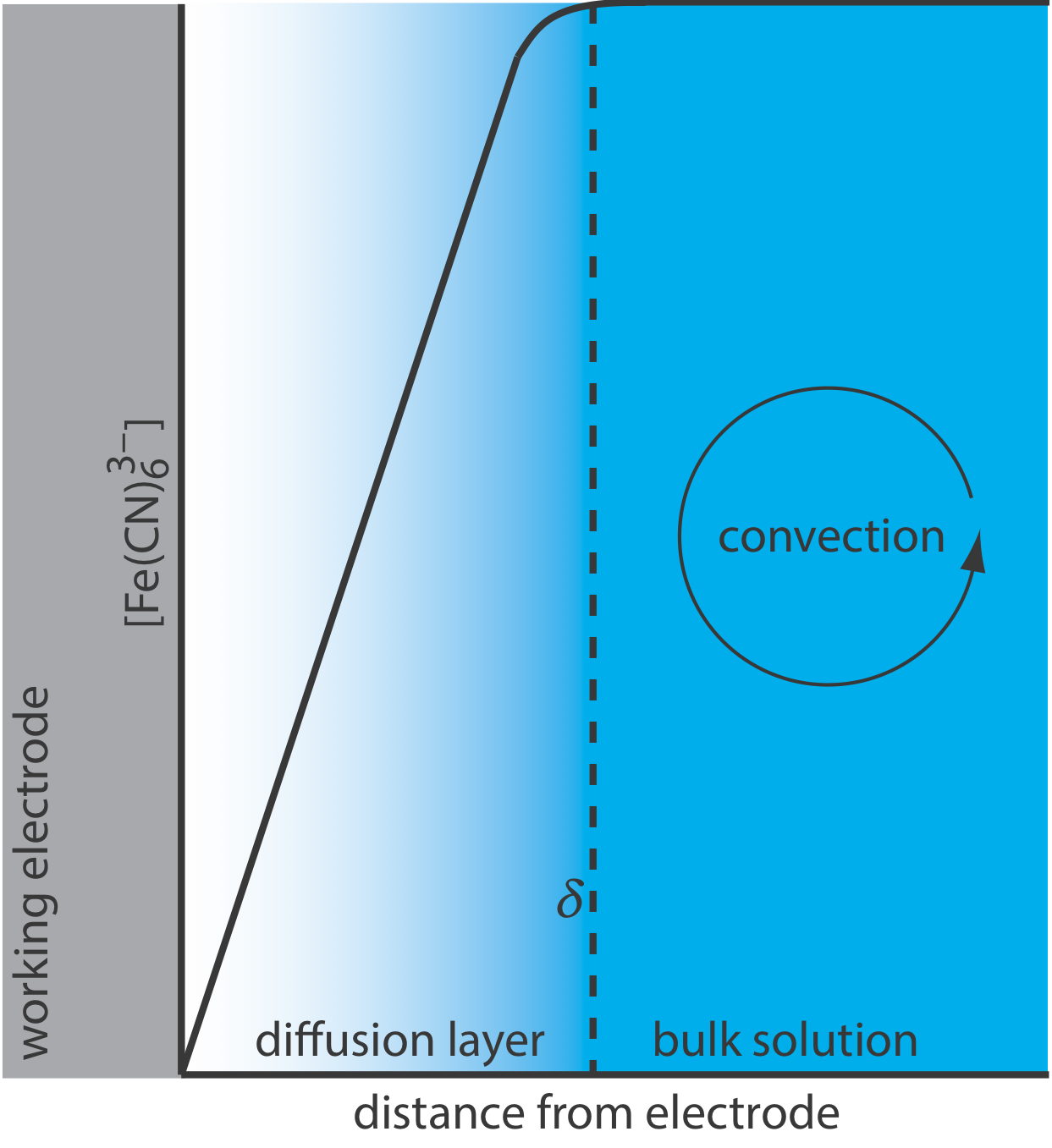
Perfiles de concentración en una solución sin agitar

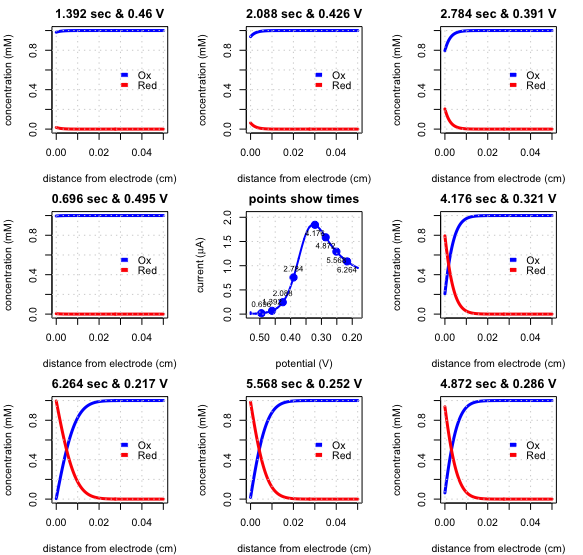
La figura\(\PageIndex{5}\) muestra el voltamograma de barrido lineal (la imagen central, que muestra la corriente en función del tiempo) y ocho instantáneas de los perfiles de concentración para la reducción de\(\text{Fe(CN)}_6^{3-}\) a\(\text{Fe(CN)}_6^{4-}\) en una solución sin agitar. El potencial inicial se estableció en +0.530 V y el potencial final se estableció en +0.182 V con una velocidad de escaneo de 0.050 V/s.

Al potencial inicial, solo\(\text{Fe(CN)}_6^{3-}\) es estable en la superficie del electrodo, y no fluye corriente. Después de 0.696 s el potencial es de 0.495 V (imagen a la izquierda del voltamograma de barrido lineal) y, debido a que\(\text{Fe(CN)}_6^{3-}\) permanece estable en la superficie del electrodo, no fluye corriente. Moviéndose en el sentido de las agujas del reloj alrededor del voltamograma de barrido lineal, el potencial aplicado se vuelve más pequeño y la concentración de\(\text{Fe(CN)}_6^{3-}\) en la superficie del electrodo disminuye y la concentración de\(\text{Fe(CN)}_6^{4-}\) aumenta. Inicialmente la pendiente del gradiente de concentración, y, por lo tanto, la corriente aumenta; a medida que la concentración de\(\text{Fe(CN)}_6^{3-}\) en la superficie del electrodo se acerca a cero, sin embargo, el gradiente de concentración se vuelve menos empinado y la corriente disminuye. El resultado es el voltamograma de barrido lineal en el centro del diagrama.

Figura\(\PageIndex{5}\): La imagen central muestra el voltamograma de barrido lineal en una solución sin agitar para la reducción de\(\text{Fe(CN)}_6^{3-}\) a\(\text{Fe(CN)}_6^{4-}\). Las imágenes restantes muestran los perfiles de concentración para\(\text{Fe(CN)}_6^{3-}\) (en azul) y para\(\text{Fe(CN)}_6^{4-}\) (en rojo) a medida que el potencial se barre de +0.530 V a +0.182 V (dispuestos en sentido horario, comenzando inmediatamente a la izquierda del voltamograma de barrido lineal.

Perfiles de concentración en una solución agitada

Si realizamos el mismo experimento que en la Figura\(\PageIndex{5}\), pero agitamos la solución, el voltamograma de barrido lineal resultante y los perfiles de concentración son los de la Figura\(\PageIndex{6}\). Agitar la solución, como vimos en la Figura\(\PageIndex{4}\) crea una capa de difusión cuyo espesor es independiente del tiempo.

Figura\(\PageIndex{6}\): La imagen central muestra el voltamograma de barrido lineal en una solución agitada para la reducción de\(\text{Fe(CN)}_6^{3-}\) a\(\text{Fe(CN)}_6^{4-}\). Las imágenes restantes muestran los perfiles de concentración para\(\text{Fe(CN)}_6^{3-}\) (en azul) y para\(\text{Fe(CN)}_6^{4-}\) (en rojo) a medida que el potencial se barre de +0.530 V a +0.182 V (dispuestos en sentido horario, comenzando inmediatamente a la izquierda del voltamograma de barrido lineal.

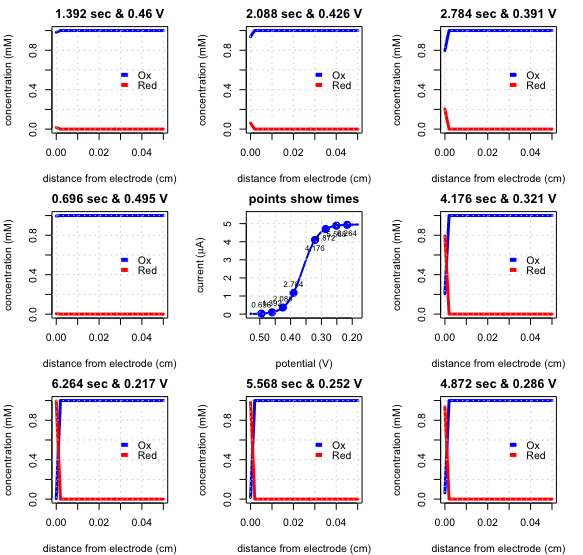
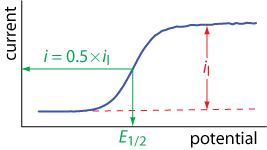
Como resultado, en lugar de la corriente pico en la Figura\(\PageIndex{5}\), la corriente alcanza un valor de estado estacionario, al que llamamos la corriente limitante,\(i_l\). El voltamograma de barrido lineal también tiene un potencial característico de media onda\(E_{1/2}\), cuando la corriente es 50% de la corriente limitante. La figura\(\PageIndex{7}\) muestra cómo se miden la corriente limitante y el potencial de media onda.

Figura\(\PageIndex{7}\): La corriente limitante y el potencial de media onda para un experimento de voltametría de barrido lineal en una solución agitada.

Corrientes Voltamétricas

Anteriormente notamos, en la Ecuación\ ref {lsv4}, que la corriente en voltamperometría de barrido lineal es proporcional a la pendiente del perfil de concentración. La corriente también es función de otras variables, como se muestra aquí para la reducción de\(\text{Fe(CN)}_6^{3-}\) a\(\text{Fe(CN)}_6^{4-}\)

\[i = \frac{ n F A D \left( \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} \right)} {\delta} \label{lsv5} \]

donde n el número de electrones en la reacción redox, F es la constante de Faraday, A es el área del electrodo, D es el coeficiente de difusión para\(\text{Fe(CN)}_6^{3-}\),\(\delta\) es el espesor de la capa de difusión, y\(\left( \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} \right)\) es la diferencia en el concentración de\( \ce{Fe(CN)6^{3-}}\) entre la solución a granel y la superficie del electrodo.

Porque\(n\),\(F\),\(A\), y\(D\) son constantes, y porque\(\delta\) es una constante si agitamos la solución, podemos escribir la Ecuación\ ref {lsv5} como

\[i = K_{\ce{Fe(CN)6^{3-}}} \left( \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} \right) \label{lsv6} \]

donde\(K_{\ce{Fe(CN)6^{3-}}}\) es una constante. Si usamos la corriente limitante, entonces\(\left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0}\) es cero, y la ecuación\ ref {lsv6} se convierte en

\[i_l = K_{\ce{Fe(CN)6^{3-}}} \left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} \label{lsv7} \]

Relaciones de corriente/voltaje para reacciones reversibles

Una reacción electroquímica reversible es aquella en la que la concentración de las especies oxidadas y reducidas en la superficie del electrodo permanecen en equilibrio termodinámico entre sí. Cuando esto es cierto, la ecuación de Nernst explica la relación entre el potencial aplicado, su concentración y el potencial estatal estándar.

La ecuación\ ref {lsv7} nos muestra que la corriente limitante es una medida de la concentración de\(\text{Fe(CN)}_6^{3-}\) solución a granel, lo que significa que podemos usar la corriente limitante para el trabajo cuantitativo. La figura\(\PageIndex{7}\) también muestra que existe una relación cualitativa entre el potencial de media onda,\(E_{1/2}\), y la corriente limitante; sin embargo, aún no está claro qué representa el potencial de media onda.

Si resolvemos la Ecuación\ ref {lsv7} para\(\left[ \ce{Fe(CN)6^{3-}} \right]_\text{bulk} \) y la sustituimos en Ecuación\ ref {lsv6} y reorganizamos, tenemos

\[ \left[ \ce{Fe(CN)6^{3-}} \right]_\text{x = 0} = \frac {i_l - i} {K_{\ce{Fe(CN)6^{3-}}}} \label{lsv8} \]

Si tomamos el mismo enfoque con\(\text{Fe(CN)}_6^{4-}\), que se forma en la solución del electrodo, entonces tenemos

\[i = -\frac{ n F A D \left( \left[ \ce{Fe(CN)6^{4-}} \right]_\text{bulk} - \left[ \ce{Fe(CN)6^{4-}} \right]_\text{x = 0} \right)} {\delta} = K_{\ce{Fe(CN)6^{4-}}} \left[ \ce{Fe(CN)6^{4-}} \right]_\text{x = 0} \label{lsv9} \]

\[ \left[ \ce{Fe(CN)6^{4-}} \right]_\text{x = 0} = \frac {-i} {K_{\ce{Fe(CN)6^{4-}}}} \label{lsv10} \]

donde el signo menos representa el perfil de concentración que tiene una pendiente negativa. Sustituyendo la ecuación\ ref {lsv9} y la ecuación\ ref {lsv10} en la ecuación\ ref {lsv1}, que es la ecuación de Nersnt, da

\[E = E^{\circ} - 0.05916 \log \frac {-i/K_{\ce{Fe(CN)6^{4-}}}} {(i_l - i)/K_{\ce{Fe(CN)6^{3-}}}} \label{lsv11} \]

\[E = E^{\circ} + 0.05916 \log \frac{K_{\ce{Fe(CN)6^{3-}}}}{K_{\ce{Fe(CN)6^{4-}}}} - 0.05916 \log \frac {i} {i_l - i} \label{lsv12} \]

Cuando\(i = \frac {i_l - i} {2}\), que es la definición de\(E_{1/2}\), Ecuación\ ref {lsv12} simplifica a

\[E_{1/2} = E^{\circ} + 0.05916 \log \frac{K_{\ce{Fe(CN)6^{3-}}}}{K_{\ce{Fe(CN)6^{4-}}}} \label{lsv13} \]

La única diferencia entre\(K_{\ce{Fe(CN)6^{3-}}}\) y\(K_{\ce{Fe(CN)6^{4-}}}\) son los coeficientes de difusión,\(D\), para\(\ce{Fe(CN)6^{3-}}\) y para\(\ce{Fe(CN)6^{4-}}\). Como estos valores deben ser similares, tenemos

\[E_{1/2} \approx E^{\circ} \label{lsv14} \]

y\(E_{1/2}\) proporciona una estimación del potencial de reducción estatal estándar.

Relaciones de corriente/voltaje para reacciones irreversibles

Cuando una reacción electroquímica no es reversible, la ecuación de Nernst ya no se aplica, lo que significa que ya no podemos asumir que el potencial de media onda proporciona una estimación para el potencial de reducción de estado estándar. La relación entre la corriente limitante y la concentración de las especies electroactivas en solución a granel sigue siendo cierta y el trabajo cuantitativo sigue siendo posible.

Ondas de Oxígeno

La presencia de oxígeno disuelto crea una complicación ya que es capaz de sufrir reacciones de reducción en la superficie del electrodo que pueden interferir con la determinación de la corriente limitante o potencial de media onda del analito. Por ejemplo, O ₂ se reduce a H ₂ O ₂ con un potencial de estado estándar de +0.695 V

\[\ce{O2}(g) + 2\ce{H+}(aq) + 2e^{-} \rightleftharpoons \ce{H2O2}(aq) \label{lsv15} \]

y H ₂ O ₂ posteriormente se reduce a H ₂ O a un potencial de estado estándar de +1.763 V.

\[\ce{H2O2}(aq) + 2\ce{H+}(aq) + 2e^{-} \rightleftharpoons 2 \ce{H2O}(aq) \label{lsv16} \]

Esta es la razón por la que una célula típica para voltametría (ver Figura 25.2.5) incluye la capacidad de pasar N ₂ a través de la solución para eliminar O ₂ disuelto. Una vez que se desairea la solución, se deja fluir N ₂ sobre la solución para evitar que O ₂ vuelva a entrar en la solución.

Aplicaciones de la voltamperometría de barrido lineal

Como aprendimos en el apartado anterior, la corriente limitante en voltamperometría de barrido lineal es proporcional a la concentración de las especies sometidas a oxidación o reducción en la superficie del electrodo, lo que la convierte en una herramienta útil para un análisis cuantitativo. Debido a que solo nos interesa la corriente limitante, la mayoría de los métodos cuantitativos simplemente mantienen el potencial del electrodo de trabajo en un valor fijo y miden la corriente limitante. Debido a que estamos midiendo la corriente en función del tiempo en lugar del potencial, estos se denominan métodos amperométricos (donde amperio es la unidad para la corriente). Aquí se recogen varios ejemplos de métodos amperométicos.

Detectores amperométricos en cromatografía y análisis de inyección de flujo

Un detector importante para la cromatografía líquida de alta resolución (HPLC) es aquel en el que la fase móvil que eluye de la columna pasa a través de una celda electroquímica de pequeño volumen en la que el electrodo de trabajo se mantiene a un potencial que oxida o reducirá los analitos. La corriente resultante se representa en función del tiempo para producir el cromatograma. Un arreglo similar se utiliza en el análisis de inyección de flujo (FIA). Consulte el Capítulo 28 (HPLC) y el Capítulo 33 (FIA) para más detalles.

Senores amperométricos

Una aplicación importante de la amperometría es en la construcción de sensores químicos. Uno de los primeros sensores amperométricos fue desarrollado en 1956 por L. C. Clark para medir O ₂ disuelto en sangre. La figura\(\PageIndex{9}\) muestra el diseño del sensor, el cual es similar a un electrodo de membrana potenciométrico. Una membrana delgada permeable a los gases se estira a través del extremo del sensor y se separa del electrodo de trabajo y del contraelectrodo por una solución delgada de KCl. El electrodo de trabajo es un cátodo de disco de Pt, y un ánodo de anillo de Ag sirve como contraelectrodo. Aunque varios gases pueden difundirse a través de la membrana, incluyendo O _{2, N 2} y CO ₂, solo el oxígeno sufre reducción en el cátodo

\[\mathrm{O}_{2}(g)+4 \mathrm{H}_{3} \mathrm{O}^{+}(a q)+4 e^{-}\rightleftharpoons 6 \mathrm{H}_{2} \mathrm{O}(l) \label{lsv17} \]

con su concentración en la superficie del electrodo llegando rápidamente a cero. La concentración de O ₂ en la superficie interna de la membrana se fija por su difusión a través de la membrana, lo que crea una corriente limitante. El resultado es una corriente de estado estacionario que es proporcional a la concentración de oxígeno disuelto. Debido a que el electrodo consume oxígeno, la muestra se agita para evitar el agotamiento de O ₂ en la superficie exterior de la membrana.

La oxidación del ánodo de Ag es la otra semirreacción.

\[\mathrm{Ag}(s)+\text{ Cl}^{-}(a q)\rightleftharpoons \mathrm{AgCl}(s)+e^{-} \nonumber \]

Figura\(\PageIndex{9}\). Sensor amperométrico Clark para determinar O ₂ disuelto. El diagrama de la derecha es una sección transversal a través del electrodo, que muestra el electrodo de anillo de Ag y el electrodo de disco de Pt.

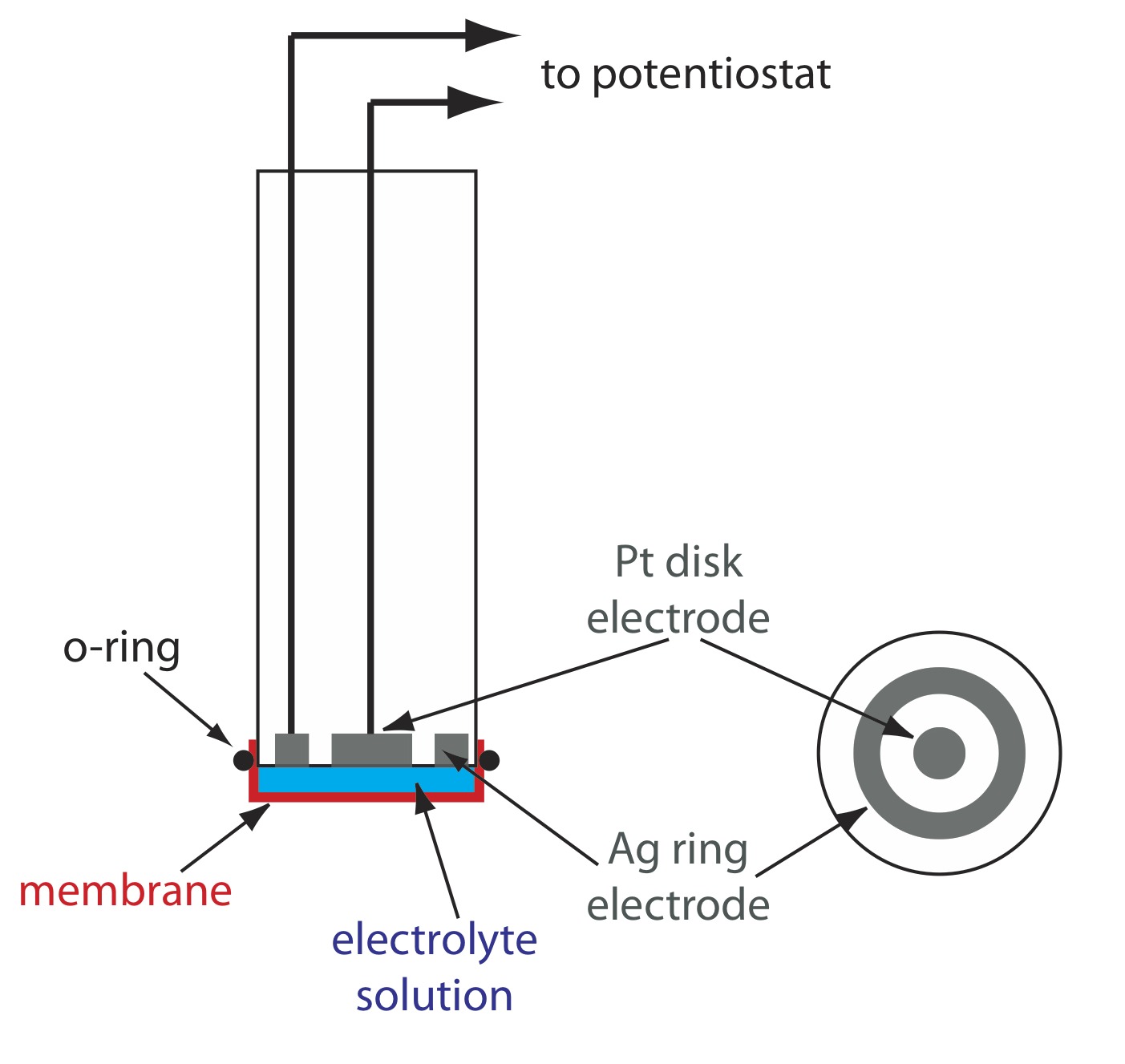
Otro ejemplo de un sensor amperométrico es un sensor de glucosa. En este sensor la membrana única de la Figura\(\PageIndex{10}\) se sustituye por tres membranas. La membrana más externa del policarbonato es permeable a la glucosa y O ₂. La segunda membrana contiene una preparación inmovilizada de glucosa oxidasa que cataliza la oxidación de la glucosa a gluconolactona y peróxido de hidrógeno.

\[\beta-\mathrm{D}-\text {glucose }(a q)+\text{ O}_{2}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \text {gluconolactone }(a q)+\text{ H}_{2} \mathrm{O}_{2}(a q) \label{lsv18} \]

El peróxido de hidrógeno se difunde a través de la membrana más interna del acetato de celulosa donde experimenta oxidación en un ánodo de Pt.

\[\mathrm{H}_{2} \mathrm{O}_{2}(a q)+2 \mathrm{OH}^{-}(a q) \rightleftharpoons \text{ O}_{2}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l)+2 e^{-} \label{lsv19} \]

La figura\(\PageIndex{10}\) resume las reacciones que tienen lugar en este sensor amperométrico. El FAD es la forma oxidada del nucleótidos de flavina adenina, el sitio activo de la enzima glucosa oxidasa, y FADH ₂ es la forma reducida del sitio activo. Tenga en cuenta que O ₂ sirve un mediador, transportando electrones al electrodo.

Figura\(\PageIndex{10}\). Esquema que muestra las reacciones mediante las cuales un biosensor amperométrico responde a la glucosa.

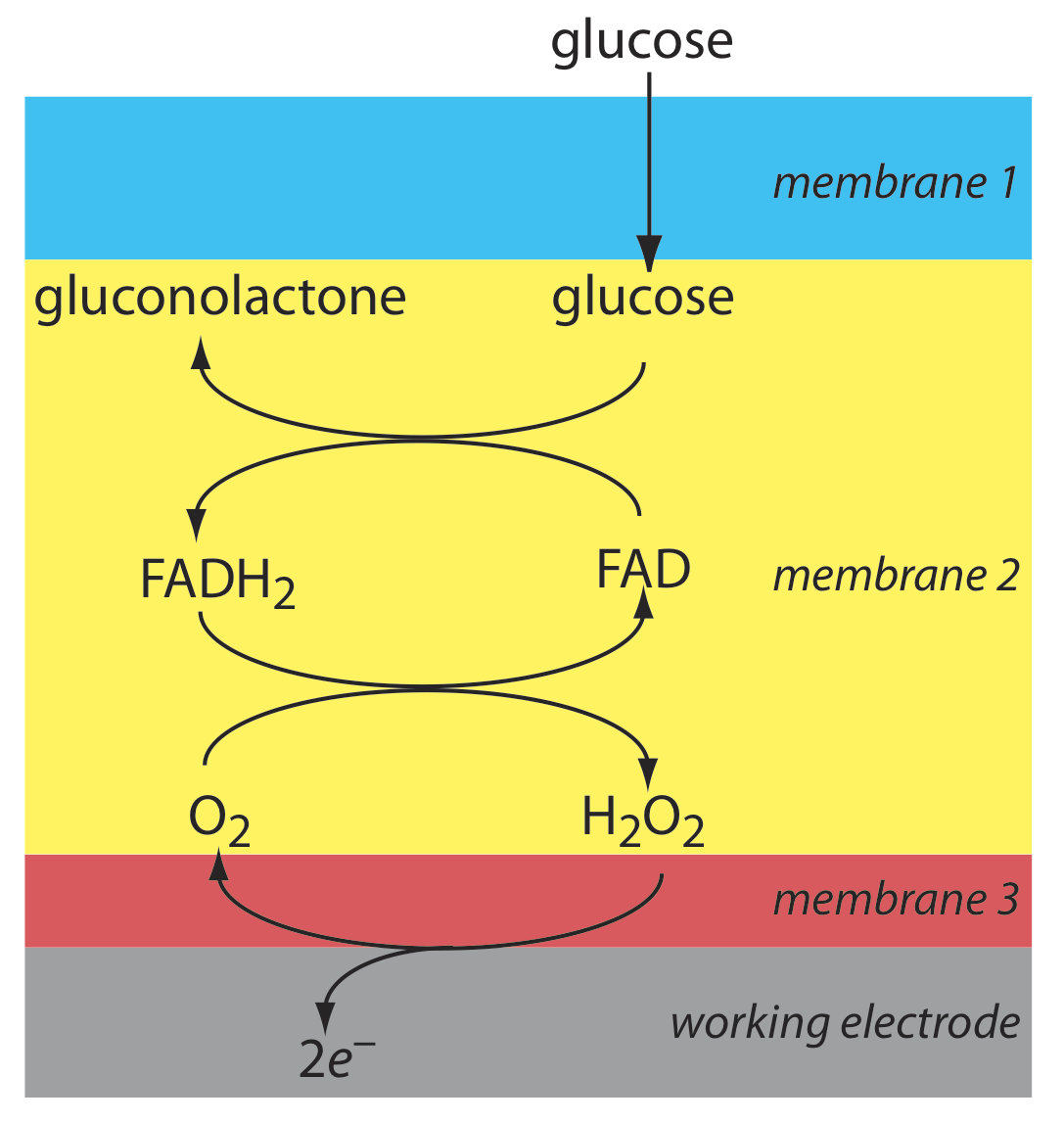
Al cambiar la enzima y el mediador, es fácil extender al sensor amperométrico en la Figura\(\PageIndex{10}\) al análisis de otros analitos. Por ejemplo, se ha desarrollado un sensor de CO ₂ utilizando un sensor amperométrico O ₂ con una membrana de dos capas, una de las cuales contiene una preparación inmovilizada de bacterias autotróficas [Karube, I.; Nomura, Y.; Arikawa, Y. Trends in Anal. Chem. 1995, 14, 295—299]. A medida que el CO ₂ se difunde a través de las membranas, es convertido en O ₂ por las bacterias, aumentando la concentración de O ₂ en el cátodo de Pt.