25.7: Aplicaciones de Voltamperometría
- Page ID
- 79030
La voltametría encuentra uso tanto para análisis cuantitativos como para análisis de caracterización. En esta sección se destacan ejemplos de cada uno.
Aplicaciones Cuantitativas
La voltametría se ha utilizado para el análisis cuantitativo de una amplia variedad de muestras, incluyendo muestras ambientales, muestras clínicas, formulaciones farmacéuticas, aceros, gasolina y aceite.
Selección de la Técnica Voltamétrica
La elección de qué técnica voltamétrica usar depende de las características de la muestra, incluyendo la concentración esperada del analito y la ubicación de la muestra. Por ejemplo, la amperometría es ideal para detectar analitos en sistemas de flujo, incluyendo el análisis in vivo de la sangre de un paciente o como sensor selectivo para el análisis rápido de un solo analito. La portabilidad de los sensores amperométricos, que son similares a los sensores potenciométricos, también los hacen ideales para estudios de campo. Aunque la voltametría cíclica se utiliza para determinar la concentración de un analito, otros métodos descritos en este capítulo son más adecuados para el trabajo cuantitativo.
La polarografía de pulso y la voltametría de pelado frecuentemente son intercambiables. La elección de qué técnica usar a menudo depende de la concentración del analito y de la precisión y precisión deseadas. Los límites de detección para la polarografía de pulso normal generalmente son del orden de 10 —6 M a 10 —7 M, y los de polarografía diferencial de pulso, escalera y polarografía de onda cuadrada están entre 10 —7 M y 10 —9 M. Debido a que concentramos el analito en voltamperometría de decapado, el límite de detección para muchos analitos es de tan solo 10 —10 M a 10 —12 M. Por otro lado, la corriente en la voltametría de extracción es mucho más sensible que la polarografía por pulsos a cambios en las condiciones experimentales, lo que puede conducir a una precisión y precisión más pobres . También podemos usar polarografía de pulso para analizar una gama más amplia de analitos inorgánicos y orgánicos porque no hay necesidad de depositar primero el analito en la superficie del electrodo.
La voltametría de decapado también sufre interferencias ocasionales cuando dos metales, como el Cu y el Zn, se combinan para formar un compuesto intermetálico en la amalgama de mercurio. El potencial de deposición de Zn es suficientemente negativo para que cualquier Cu 2 + en la muestra también se deposite en la gota o película de mercurio, lo que lleva a la formación de compuestos intermetálicos como CuZn y CuZn 2. Durante la etapa de decapado, el zinc en los compuestos intermetálicos se desploma a potenciales cercanos al del cobre, disminuyendo la corriente para el zinc a su potencial habitual y aumentando la corriente aparente para el cobre. Es posible superar este problema añadiendo un elemento que forme un compuesto intermetálico más fuerte con el metal interferente. Así, agregar Ga 3 + minimiza la interferencia de Cu al analizar Zn al formar un compuesto intermetálico de Cu y Ga.
Corrección para la Corriente Residual
En cualquier análisis cuantitativo debemos corregir la señal del analito para señales que surjan de otras fuentes. La corriente total, i tot, en voltamperometría consta de dos partes: la corriente de la oxidación o reducción del analito, i A, y una corriente de fondo o residual, i r.
\[i_{t o t}=i_{A}+i_{r} \label{app1} \]
La corriente residual, a su vez, tiene dos fuentes. Una fuente es una corriente faradaica de la oxidación o reducción de los interferentes traza en la muestra, i int. La otra fuente es la corriente de carga, i ch, que acompaña un cambio en el potencial del electrodo de trabajo.
\[i_{r}=i_{\mathrm{int}}+i_{c h} \label{app2} \]
Podemos minimizar la corriente faradaica debida a las impurezas preparando cuidadosamente la muestra. Por ejemplo, una impureza importante es el O 2 disuelto, que sufre una reducción en dos etapas: primero a H 2 O 2 a un potencial de —0.1 V versus el SCE, y luego a H 2 O a un potencial de —0.9 V contra el SCE. Eliminar O 2 disuelto burbujeando un gas inerte como N 2 a través de la muestra elimina esta interferencia. Después de retirar el O 2 disuelto, mantener una manta de N 2 sobre la parte superior de la solución evita que O 2 vuelva a entrar en la solución.
Existen dos métodos para compensar la corriente residual. Un método consiste en medir la corriente total a potenciales donde la corriente faradaica del analito es cero y extrapolarla a otros potenciales. Este es el método mostrado en la Figura 25.3.7. Una ventaja de extrapolar es que no necesitamos adquirir datos adicionales. Una desventaja importante es que una extrapolación supone que cualquier cambio en la corriente residual con potencial es predecible, lo que puede no ser el caso. Un segundo enfoque, y más riguroso, es obtener un voltamograma para un blanco apropiado. La corriente residual del blanco se resta entonces de la corriente total de la muestra.
Análisis para componentes individuales
El análisis de una muestra con un solo analito es sencillo utilizando cualquiera de los métodos de estandarización discutidos en el Capítulo 1.
La concentración de As (III) en agua se determina mediante polarografía diferencial de pulso en HCl 1 M. El potencial inicial se establece en —0.1 V versus el SCE y se escanea hacia potenciales más negativos a una velocidad de 5 mV/s. La reducción de As (III) a As (0) ocurre a un potencial de aproximadamente —0.44 V frente al SCE. Las corrientes pico para un conjunto de soluciones estándar, corregidas para la corriente residual, se muestran en la siguiente tabla.
| [Como (III)] (µM) | i p (µM) |
|---|---|
| 1.00 | 0.298 |
| 3.00 | 0.947 |
| 6.00 | 1.83 |
| 9.00 | 2.72 |
¿Cuál es la concentración de As (III) en una muestra de agua si su pico de corriente es de 1.37 μA?
Solución
La regresión lineal da la curva de calibración mostrada en la Figura\(\PageIndex{1}\), con una ecuación de
\[i_{p}=0.0176+3.01 \times[\mathrm{As}(\mathrm{III})] \nonumber \]
Sustituyendo la corriente pico de la muestra en la ecuación de regresión da la concentración de As (III) como 4.49 μM.
Análisis multicomponente
La voltametría es una técnica particularmente atractiva para el análisis de muestras que contienen dos o más analitos. Siempre que los analitos se comporten de forma independiente, el voltamograma de una mezcla multicomponente es una suma de los voltamogramas individuales de cada analito. Como se muestra en la Figura\(\PageIndex{2}\), si la separación entre los potenciales de media onda o entre los potenciales de pico es suficiente, podemos determinar la presencia de cada analito como si fuera el único analito en la muestra. La separación mínima entre los potenciales de media onda o los potenciales de pico para dos analitos depende de varios factores, incluyendo el tipo de electrodo y la señal de excitación potencial. Para la polarografía normal la separación es de al menos ±0.2—0.3 V, y la voltametría diferencial de pulso requiere una separación mínima de ±0.04—0.05 V.
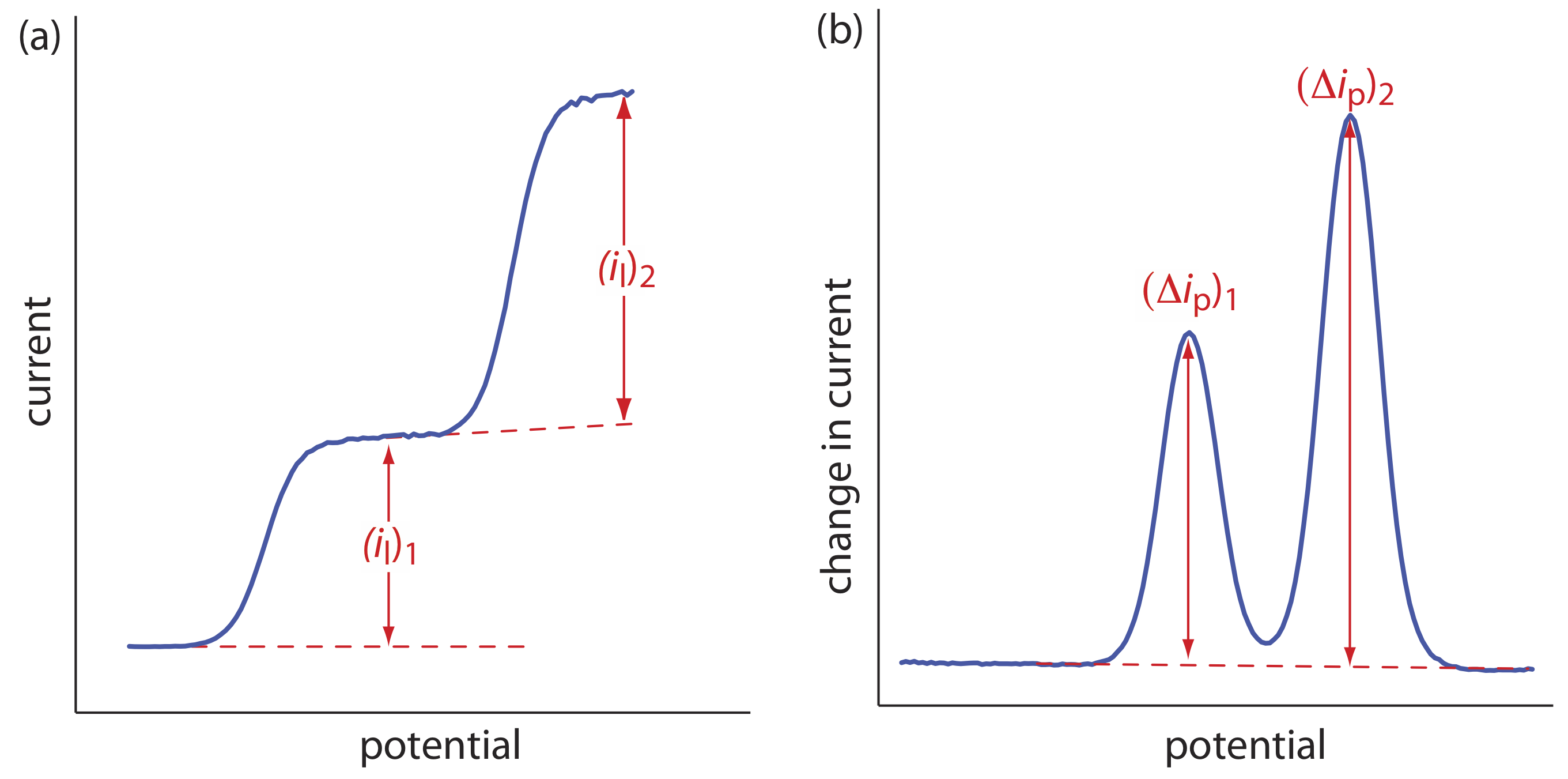
Si los voltamogramas para dos analitos no están suficientemente separados, puede ser posible un análisis simultáneo. Un ejemplo de este enfoque se esboza el siguiente ejemplo.
El análisis polarográfico de pulso diferencial de una mezcla de indio y cadmio en HCl 0.1 M se complica por el solapamiento de sus respectivos voltamogramas [Lanza P. J. Chem. Educ. 1990, 67, 704—705]. El potencial pico para indio está en —0.557 V y el de cadmio está en —0.597 V. Cuando se analiza un estándar de indio de 0.800 ppm,\(\Delta i_p\) (en unidades arbitrarias) es 200.5 a —0.557 V y 87.5 a —0.597 V en relación con un electorde de referencia Ag/AgCl saturado. Una solución estándar de 0.793 ppm de cadmio tiene un\(\Delta i_p\) de 58.5 a —0.557 V y 128.5 a —0.597 V. Cuál es la concentración de indio y cadmio en una muestra si\(\Delta i_p\) es 167.0 a un potencial de —0.557 V y 99.5 a un potencial de —0.597V.
Solución
El cambio en la corriente,\(\Delta i_p\), en la polarografía diferencial de pulso es una función lineal de la concentración del analito
\[\Delta i_{p}=k_{A} C_{A} \nonumber \]
donde k A es una constante que depende del analito y del potencial aplicado, y C A es la concentración del analito. Para determinar las concentraciones de indio y cadmio en la muestra primero debemos encontrar el valor de k A para cada analito en cada potencial. Por simplicidad identificaremos el potencial de —0.557 V como E 1, y el de —0.597 V como E 2. Los valores de k A son
\[\begin{aligned} k_{\mathrm{In}, E_{1}} &=\frac{200.5}{0.800 \ \mathrm{ppm}}=250.6 \ \mathrm{ppm}^{-1} \\ k_{\mathrm{In}, E_{2}} &=\frac{87.5}{0.800 \ \mathrm{ppm}}=109.4 \ \mathrm{ppm}^{-1} \\ k_{\mathrm{Cd} E_{1}} &=\frac{58.5}{0.793 \ \mathrm{ppm}}=73.8 \ \mathrm{ppm}^{-1} \\ k_{\mathrm{Cd} E_{2}} &=\frac{128.5}{0.793 \ \mathrm{ppm}}=162.0 \ \mathrm{ppm}^{-1} \end{aligned} \nonumber \]
A continuación, escribimos ecuaciones simultáneas para la corriente en los dos potenciales.
\[\begin{array}{l}{\Delta i_{E_{1}}=167.0=250.6 \ \mathrm{ppm}^{-1} \times C_{\mathrm{In}}+73.8 \ \mathrm{ppm}^{-1} \times C_{\mathrm{Cd}}} \\ {\triangle i_{E_{2}}=99.5=109.4 \ \mathrm{ppm}^{-1} \times C_{\mathrm{In}}+162.0 \ \mathrm{ppm}^{-1} \times C_{\mathrm{Cd}}}\end{array} \nonumber \]
Resolviendo las ecuaciones simultáneas, que se deja como ejercicio, da la concentración de indio como 0.606 ppm y la concentración de cadmio como 0.205 ppm.
Muestras Ambientales
La voltametría es una de varias técnicas analíticas importantes para el análisis de metales traza en muestras ambientales, incluyendo agua subterránea, lagos, ríos y arroyos, agua de mar, lluvia y nieve. Los límites de detección en el nivel de partes por billón son rutinarios para muchos metales traza usando polarografía diferencial de pulso, con voltametría de extracción anódica que proporciona límites de detección de partes por billón para algunos metales traza.
Una aplicación ambiental interesante de la voltametría de extracción anódica es la determinación de la forma química de un metal traza dentro de una muestra de agua. La especiación es importante porque la biodisponibilidad, la toxicidad y la facilidad de transporte de un metal traza a menudo dependen de su forma química. Por ejemplo, un metal traza que está fuertemente unido a partículas coloidales generalmente no es tóxico porque no está disponible para formas de vida acuáticas. Desafortunadamente, la voltametría de extracción anódica no puede distinguir la forma química exacta de un metal traza porque especies estrechamente relacionadas, como Pb 2 + y PbCl +, producen un solo pico de extracción. En cambio, los metales traza se dividen en categorías “definidas operativamente” que tienen importancia ambiental.
Definido operacionalmente significa que un analito se divide en categorías por los métodos específicos utilizados para aislarlo de la muestra. Existen muchos ejemplos de definiciones operativas en la literatura ambiental. La distribución de los metales traza en suelos y sedimentos, por ejemplo, a menudo se define en términos de los reactivos utilizados para extraerlos; así, se puede encontrar una definición operativa para Zn 2 + en un sedimento lacustre como el extraído con acetato de sodio 1.0 M, o el extraído usando 1.0 M HCl.
Aunque existen muchos esquemas de especiación en la literatura ambiental, consideraremos uno propuesto por Batley y Florence [ver (a) Batley, G. E.; Florence, T. M. Anal. A lett. 1976, 9, 379—388; b) Batley, G. E.; Florence, T. M. Talanta 1977, 24, 151—158; c) Batley, G. E.; Florence, T. M. Anal. Chem. 1980, 52, 1962-1963; d) Florence, T. M., Batley, G. E.; CRC Crit. Rev. Anal. Chem. 1980, 9, 219—296]. Este esquema, que se esboza en la Tabla\(\PageIndex{2}\), combina la voltametría de decapado anódica con intercambio iónico e irradiación UV, dividiendo los metales traza solubles en siete grupos. En la primera etapa, la voltamperometría de extracción anódica en un tampón de ácido acético pH 4.8 diferencia entre metales lábiles y metales no lábiles. Solo los metales lábiles, aquellos presentes como iones hidratados, complejos débilmente unidos o débilmente adsorbidos sobre superficies coloidales, se depositan en el electrodo y dan lugar a una señal. La concentración total de metales se determina por ASV después de digerir la muestra en HNO 3 2 M durante 5 min, lo que convierte todos los metales en una forma lábil a ASV.
Una resina de intercambio iónico Chelex-100 diferencia aún más entre metales fuertemente unidos, generalmente metales unidos a sólidos inorgánicos y orgánicos, pero también aquellos fuertemente unidos a ligandos quelantes, y metales unidos más flojamente. Finalmente, la radiación UV diferencia entre metales unidos a fases orgánicas y fases inorgánicas. El análisis de muestras de agua de mar, por ejemplo, sugiere que el cadmio, el cobre y el plomo están presentes principalmente como complejos orgánicos lábiles o como adsorbatos lábiles en coloides orgánicos (Grupo II en la Tabla\(\PageIndex{1}\)).
La polarografía diferencial de pulsos y la voltametría de decapado se utilizan para determinar trazas de metales en partículas transportadas por el aire, cenizas volantes incineradoras, rocas, minerales y sedimentos. Los metales traza, por supuesto, primero se ponen en solución usando una digestión o una extracción.
Los sensores amperométricos también se utilizan para analizar muestras ambientales. Por ejemplo, el sensor O 2 disuelto descrito anteriormente se utiliza para determinar el nivel de oxígeno disuelto y la demanda bioquímica de oxígeno, o DBO, de aguas y aguas residuales. Esta última prueba, que es una medida de la cantidad de oxígeno que requieren las bacterias acuáticas a medida que descomponen la materia orgánica, es importante a la hora de evaluar la eficiencia de una planta de tratamiento de aguas residuales y para monitorear la contaminación orgánica en aguas naturales. Un DBO alto sugiere que el agua tiene una alta concentración de materia orgánica. La descomposición de esta materia orgánica puede agotar seriamente el nivel de oxígeno disuelto en el agua, afectando negativamente a la vida acuática. Otros sensores amperométricos están disponibles para monitorear tensioactivos aniónicos en agua, y CO 2, H 2 SO 4 y NH 3 en gases atmosféricos.
Muestras Clínicas
La polarografía diferencial de pulso y la voltametría de extracción se utilizan para determinar la concentración de metales traza en una variedad de muestras clínicas, incluyendo sangre, orina y tejido. La determinación de plomo en la sangre es de considerable interés debido a las preocupaciones sobre el envenenamiento por plomo. Debido a que la concentración de plomo en la sangre es tan pequeña, la voltametría de extracción anódica frecuentemente es la técnica más apropiada. El análisis se complica, sin embargo, por la presencia de proteínas que pueden adsorberse al electrodo de mercurio, inhibiendo ya sea la deposición o el arrastre de plomo. Además, las proteínas pueden prevenir la electrodeposición de plomo a través de la formación de complejos estables y no lábiles. Digerir y macerar la muestra de sangre mini- empaña este problema. La polarografía diferencial de pulso es útil para el análisis cuantitativo rutinario de fármacos en fluidos biológicos, a concentraciones inferiores a 10 —6 M [Brooks, M. A. “Aplicación de la Electroquímica al Análisis Farmacéutico”, Capítulo 21 en Kissinger, P. T.; Heinemann, W. R., eds. Técnicas de Laboratorio en Química Electroanalítica, Marcel Dekker, Inc.: Nueva York, 1984, pp 539—568.]. Los sensores amperométricos que utilizan catalizadores enzimáticos también tienen muchos usos clínicos, varios ejemplos de los cuales se muestran en la Tabla\(\PageIndex{2}\).
Muestras Diversas
Además de las muestras ambientales y clínicas, la polarografía diferencial de pulso y la voltametría de decapado se utilizan para el análisis de metales traza en otras muestras, incluyendo alimentos, aceros y otras aleaciones, gasolina, residuos de pólvora y productos farmacéuticos. La voltametría es una técnica importante para el análisis cuantitativo de compuestos orgánicos, particularmente en la industria farmacéutica donde se utiliza para determinar la concentración de fármacos y vitaminas en formulaciones. Por ejemplo, se dispone de métodos voltamétricos para el análisis cuantitativo de vitamina A, niacinamida y riboflavina. Cuando el compuesto de interés no es electroactivo, a menudo se puede derivatizar a una forma electroactiva. Un ejemplo es la determinación polarográfica de pulso diferencial de sulfanilamida, la cual se convierte en un colorante azo electroactivo por acoplamiento con ácido sulfámico y 1-naftol.
En la sección anterior aprendimos a usar la voltametría para determinar la concentración de un analito en una variedad de muestras diferentes. También podemos utilizar la voltametría para caracterizar las propiedades de un analito, incluyendo verificar su reversibilidad electroquímica, determinar el número de electrones transferidos durante su oxidación o reducción, y determinar su constante de equilibrio en una reacción química acoplada.
Aplicaciones de Caracterización
En una aplicación de caracterización estudiamos las propiedades de un sistema. Aquí se describen tres ejemplos: determinar si una reacción redox es electroquímicamente reversible, determinar el número de electrones involucrados en la reacción redox y estudiar la complejación metal-ligando.
Reversibilidad Electroquímica y Determinación de n
Anteriormente en este capítulo derivamos una relación entre E 1/2 y el potencial de estado estándar para una pareja redox usando la ecuación de Nernst, señalando que una reacción redox debe ser electroquímicamente reversible. ¿Cómo podemos saber si una reacción redox es reversible observando su voltamograma? Como aprendimos en el Capítulo 25.3, para una reacción redox reversible la relación entre potencial y corriente es
\[E=E_{½} - \frac{0.05916}{n} \log \frac{i}{i_{l} - i} \label{app3} \]
Si una reacción es electroquímicamente reversible, una gráfica de E versus\(\log \frac{i}{i_l - i}\) es una línea recta con una pendiente de —0.05916/ n. Además, la pendiente debe dar un valor entero para n.
Los siguientes datos se obtuvieron de un voltamograma hidrodinámico de barrido lineal de una reacción de reducción reversible.
| E (V frente a SCE) | corriente (μA) |
|---|---|
| —0.358 | 0.37 |
| —0.372 | 0.95 |
| —0.382 | 1.71 |
| —0.400 | 3.48 |
| —0.410 | 4.20 |
| —0.435 | 4.97 |
La corriente límite es de 5.15 μA. Mostrar que la reacción de reducción es reversible, y determinar valores para n y para E 1/2.
Solución
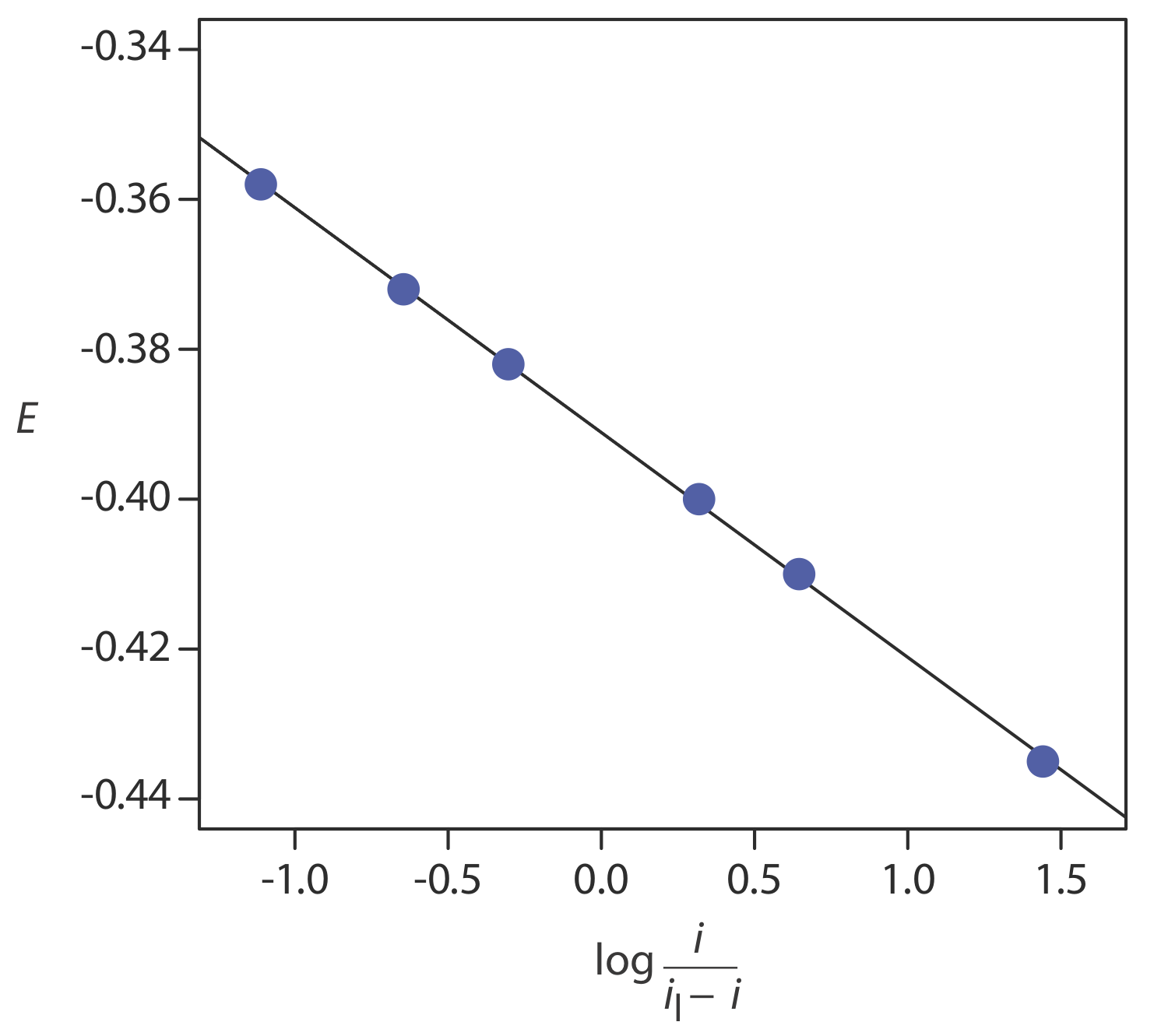
La figura\(\PageIndex{3}\) muestra una gráfica de E versus\(\log \frac{i}{i_l - i}\). Debido a que el resultado es una línea recta, sabemos que la reacción es electroquímicamente reversible bajo las condiciones del experimento. Un análisis de regresión lineal da la ecuación para la línea recta como
\[E=-0.391 \mathrm{V}-0.0300 \log \frac{i}{i_{l}-i} \nonumber \]
De la Ecuación\ ref {app3}, la pendiente es equivalente a —0.05916/ n; resolviendo para n da un valor de 1.97, o 2 electrones. De la Ecuación\ ref {app3} también sabemos que E 1/2 es la intersección y para una gráfica de E versus\(\log \frac{i}{i_l - i}\); así, E 1/2 para los datos en este ejemplo es —0.391 V versus el SCE.
También podemos utilizar voltamperometría cíclica para evaluar la reversibilidad electroquímica observando la diferencia entre los potenciales máximos para los escaneos anódicos y catódicos. Para una reacción electroquímicamente reversible, la siguiente ecuación es cierta.
\[\Delta E_{p}=E_{p, a}-E_{p, c}=\frac{0.05916 \ \mathrm{V}}{n} \label{app4} \]
Como ejemplo, para una reducción de dos electrones esperamos una\(\Delta E_p\) de aproximadamente 29.6 mV. Para una reacción electroquímicamente irreversible el valor de\(\Delta E_p\) es mayor de lo esperado.
Determinación de constantes de equilibrio para reacciones químicas acopladas
Otra aplicación importante de la voltametría es determinar la constante de equilibrio para una reacción en solución que se acopla a una reacción redox. La presencia de la reacción en solución afecta la facilidad de transferencia de electrones en la reacción redox, desplazando E 1/2 a un potencial más negativo o a un potencial más positivo. Consideremos, por ejemplo, la reducción de O a R
\[O+n e^{-} \rightleftharpoons R \label{app5} \]
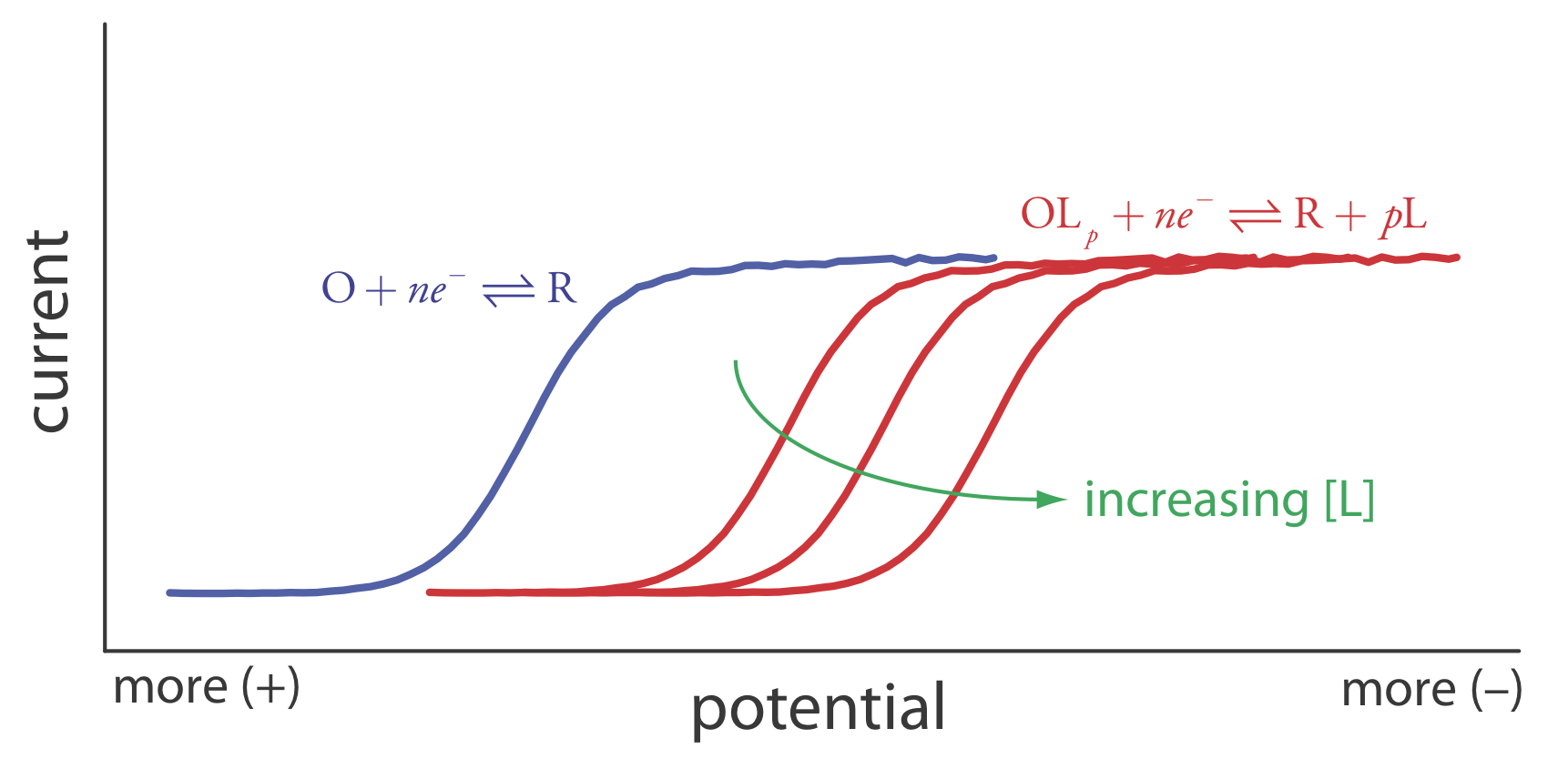
el voltamograma para el cual se muestra en la Figura\(\PageIndex{4}\). Si introducimos un ligando, L, que forma un complejo fuerte con O, entonces también debemos considerar la reacción
\[O+p L\rightleftharpoons O L_{p} \label{app6} \]
En presencia del ligando, la reacción redox global es
\[O L_{p}+n e^{-} \rightleftharpoons R+p L \label{app7} \]
Debido a su estabilidad, la reducción del complejo OL p es menos favorable que la reducción de O. Como se muestra en la Figura\(\PageIndex{4}\), el voltamograma resultante se desplaza a un potencial que es más negativo que el de O. Además, el cambio en el voltamograma aumenta a medida que aumentamos la concentración del ligando.
Podemos usar este cambio en el valor de E 1/2 para determinar tanto la estequiometría como la constante de formación para un complejo metal-ligando. Para derivar una relación entre las variables relevantes comenzamos con dos ecuaciones: la ecuación de Nernst para la reducción de O
\[E=E_{O / R}^{\circ}-\frac{0.05916}{n} \log \frac{[R]_{x=0}}{[O]_{x=0}} \label{app8} \]
y la constante de estabilidad,\(\beta_p\) para el complejo metal-ligando en la superficie del electrodo.
\[\beta_{p} = \frac{\left[O L_p\right]_{x = 0}}{[O]_{x = 0}[L]_{x = 0}^p} \label{app9} \]
En ausencia de ligando el potencial de media onda ocurre cuando [R] x = 0 y [O] x = 0 son iguales; así, a partir de la ecuación de Nernst tenemos
\[\left(E_{1 / 2}\right)_{n c}=E_{O / R}^{\circ} \label{app10} \]
donde el subíndice “nc” significa que el complejo no está presente. Cuando el ligando está presente debemos dar cuenta de su efecto sobre la concentración de O. Resolviendo la Ecuación\ ref {app9} para [O] x = 0 y sustituyendo en la Ecuación\ ref {app8} da
\[E=E_{O/R}^{\circ}-\frac{0.05916}{n} \log \frac{[R]_{x=0}[L]_{x=0}^{p} \beta_{p}}{\left[O L_{p}\right]_{x=0}} \label{app11} \]
Si la constante de formación es suficientemente grande, de tal manera que esencialmente todo O está presente como el complejo OL p, entonces\([R]_{x = 0}\) y\([OL_p]_{x = 0}\) son iguales en el potencial de media onda, y la ecuación\ ref {app11} simplifica a
\[\left(E_{1 / 2}\right)_{c} = E_{O/R}^{\circ} - \frac{0.05916}{n} \log{} [L]_{x=0}^{p} \beta_{p} \label{app12} \]
donde el subíndice “c” indica que el complejo está presente. Definir\(\Delta E_{1/2}\) como
\[\triangle E_{1 / 2}=\left(E_{1 / 2}\right)_{c}-\left(E_{1 / 2}\right)_{n c} \label{app13} \]
y sustituyendo la ecuación\ ref {app10} y la ecuación\ ref {app12} y expandiendo el término logarítmico nos deja con la siguiente ecuación.
\[\Delta E_{1 / 2}=-\frac{0.05916}{n} \log \beta_{p}-\frac{0.05916 p}{n} \log {[L]} \label{app14} \]
Una gráfica\(\Delta E_{1/2}\) versus log [L] es una línea recta, con una pendiente que es función del coeficiente estequiométrico del complejo metal-ligando, p, y una intersección y que es función de su constante de formación\(\beta_p\).
Un voltamograma para la reducción de dos electrones (n = 2) de un metal, M, tiene un potencial de media onda de —0.226 V versus el SCE. En presencia de un exceso de ligando, L, se registran los siguientes potenciales de media onda.
| [L] (M) | (E 1/2) c (V frente a SCE) |
|---|---|
| 0.020 | —0.494 |
| 0.040 | —0.512 |
| 0.060 | —0.523 |
| 0.080 | —0.530 |
| 0.100 | —0.536 |
Determinar la estequiometría del complejo metal-ligando y su constante de formación.
Solución
Comenzamos calculando valores de\(\Delta E_{1/2}\) usar la Ecuación\ ref {app13}, obteniendo los valores en la siguiente tabla.
| [L] (M) | \(\Delta E_{1/2}\)(V vs. SCE) |
|---|---|
| 0.020 | \ (\ Delta E_ {1/2}\) (V vs SCE) ">—0.268 |
| 0.040 | \ (\ Delta E_ {1/2}\) (V vs SCE) ">—0.286 |
| 0.060 | \ (\ Delta E_ {1/2}\) (V vs SCE) ">—0.297 |
| 0.080 | \ (\ Delta E_ {1/2}\) (V vs SCE) ">—0.304 |
| 0.100 | \ (\ Delta E_ {1/2}\) (V vs SCE) ">—0.310 |
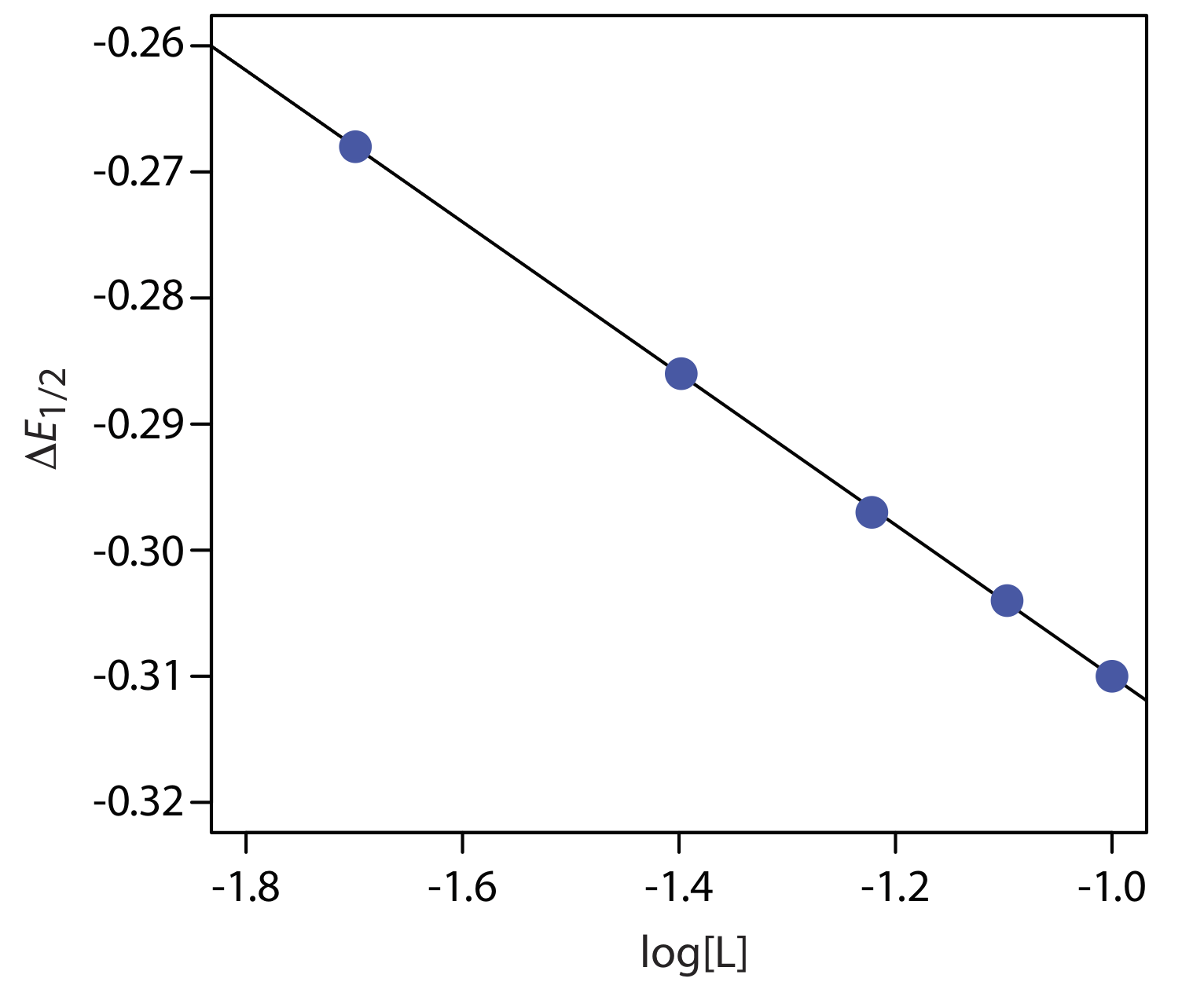
La figura\(\PageIndex{5}\) muestra la gráfica resultante de\(\Delta E_{1/2}\) como una función del log [L]. Un análisis de regresión lineal da la ecuación para la línea recta como
\[\triangle E_{1 / 2}=-0.370 \mathrm{V}-0.0601 \log {[L]} \nonumber \]
De la Ecuación\ ref {app14} sabemos que la pendiente es igual a —0.05916 p/n. Usando la pendiente y n = 2, resolvemos para p obteniendo un valor de 2.03 ≈ 2. La estequiometría del complejo, por lo tanto, es ML 2. También sabemos, por la Ecuación\ ref {app14}, que la intersección y es equivalente a — (0.05916/ n) log\(\beta_p\). Resolviendo para\(\beta_2\) da una constante de formación de\(3.2 \times 10^{12}\).
La voltametría cíclica es una de las técnicas electroquímicas más potentes para explorar el mecanismo de las reacciones electroquímicas y químicas acopladas. El tratamiento de este aspecto de la voltametría cíclica está más allá del nivel de este texto, aunque puede consultar los recursos adicionales de este capítulo para obtener información adicional.