11.2: Métodos Potenciométricos
- Page ID
- 75845
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En potenciometría medimos el potencial de una celda electroquímica bajo condiciones estáticas. Debido a que ninguna corriente, o solo una corriente insignificante, fluye a través de la celda electroquímica, su composición permanece sin cambios. Por esta razón, la potenciometría es un método cuantitativo útil de análisis. Las primeras aplicaciones potenciométricas cuantitativas aparecieron poco después de la formulación, en 1889, de la ecuación de Nernst, que relaciona el potencial de una célula electroquímica con la concentración de especies electroactivas en la célula [Stork, J. T. Anal. Chem. 1993, 65, 344A—351A].
Para una introducción en línea a gran parte del material de esta sección, consulte Electroquímica Analítica: Potenciometría de Erin Gross, Richard S. Kelly, y Donald M. Cannon, Jr., un recurso que forma parte de la Biblioteca Digital de Ciencias Analíticas.
La potenciometría inicialmente se restringió a los equilibrios redox en los electrodos metálicos, lo que limitó su aplicación a unos pocos iones. En 1906, Cremer descubrió que la diferencia de potencial a través de una fina membrana de vidrio es una función del pH cuando lados opuestos de la membrana están en contacto con soluciones que tienen diferentes concentraciones de H 3 O +. Este descubrimiento condujo al desarrollo del electrodo de pH de vidrio en 1909. Otros tipos de membranas también producen potenciales útiles. Por ejemplo, en 1937 Kolthoff y Sanders mostraron que se puede utilizar un pellet de AgCl para determinar la concentración de Ag +. Los electrodos basados en potenciales de membrana se denominan electrodos selectivos de iones, y su desarrollo continuo extiende la potenciometría a una amplia gama de analitos.
Mediciones Potenciométricas
Como se muestra en la Figura 11.1.3, utilizamos un potenciómetro para determinar la diferencia entre el potencial de dos electrodos. El potencial de un electrodo, el electrodo de trabajo o indicador, responde a la actividad del analito y el otro electrodo, el contador o electrodo de referencia, tiene un potencial fijo conocido. En esta sección se presentan las convenciones para describir las celdas electroquímicas potenciométricas y la relación entre el potencial medido y la actividad del analito.
En el Capítulo 6 señalamos que la posición de equilibrio de una reacción química es una función de las actividades de los reactivos y productos, no de sus concentraciones. Para ser correctos, debemos escribir la ecuación de Nernst en términos de actividades. Entonces, ¿por qué no usamos las actividades del Capítulo 9 cuando calculamos las curvas de valoración redox? Hay dos razones para esa elección. Primero, las concentraciones son siempre más fáciles de calcular que las actividades. Segundo, en una valoración redox determinamos la concentración del analito desde el punto final de la titulación, no desde el potencial en el punto final. La única razón para calcular una curva de valoración es evaluar su factibilidad y ayudarnos a seleccionar un indicador útil. En la mayoría de los casos, el error que introducimos asumiendo que la concentración y la actividad son idénticas es demasiado pequeño para ser una preocupación significativa.
En potenciometría no podemos pasar por alto la diferencia entre actividad y concentración. Más adelante en esta sección consideraremos cómo podemos diseñar un método potenciométrico para que podamos ignorar la diferencia entre actividad y concentración. Consulte el Capítulo 6.9 para revisar nuestra discusión anterior de actividad y concentración.
Celdas Electroquímicas Potenciométricas
Un diagrama esquemático de una celda electroquímica potenciométrica típica se muestra en la Figura 11.2.1 . La celda electroquímica consta de dos medias celdas, cada una de las cuales contiene un electrodo sumergido en una solución de iones cuyas actividades determinan el potencial del electrodo. Un puente salino que contiene un electrolito inerte, como KCl, conecta las dos medias celdas. Los extremos del puente salino se fijan con fritas porosas, que permiten que los iones del electrolito se muevan libremente entre las medias celdas y el puente salino. Este movimiento de iones en el puente salino completa el circuito eléctrico.
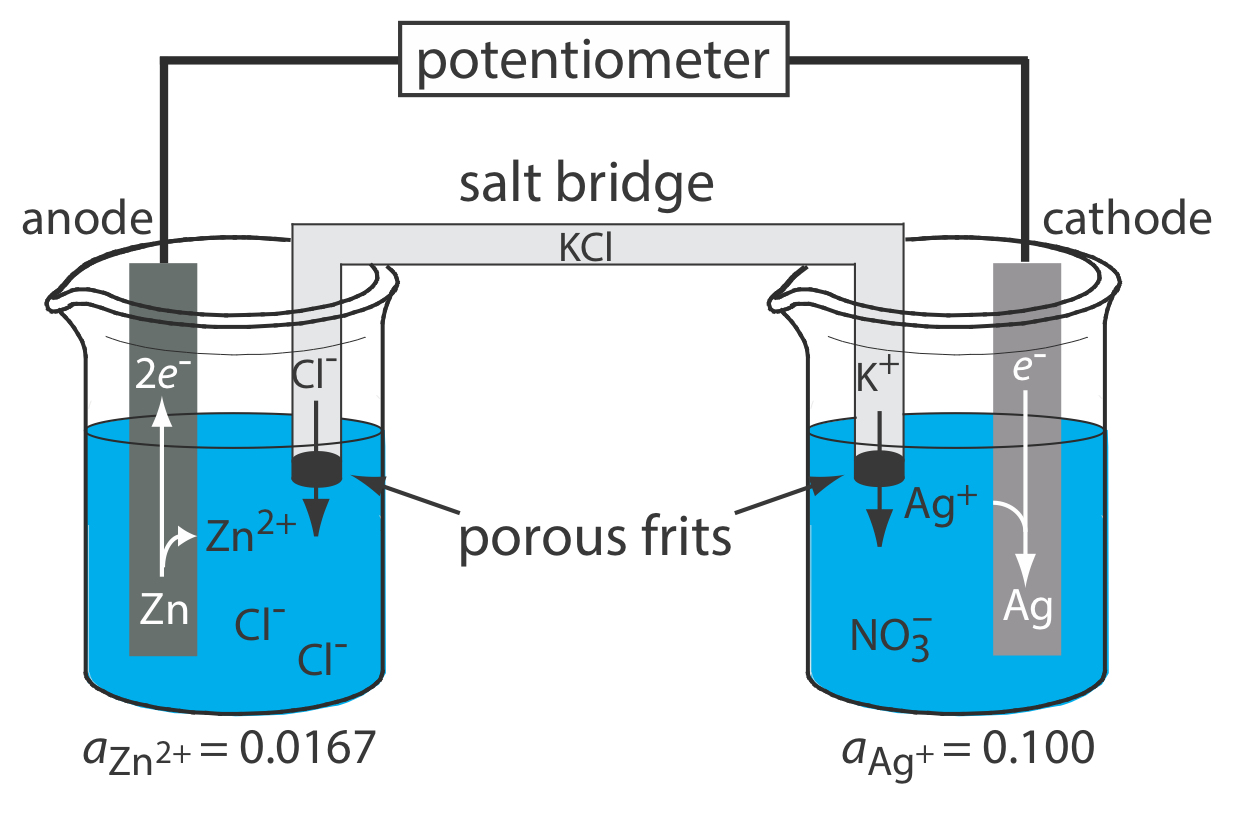
Por convención, identificamos el electrodo de la izquierda como ánodo y le asignamos la reacción de oxidación; así
\[\mathrm{Zn}(s) \rightleftharpoons \text{ Zn}^{2+}(a q)+2 e^{-} \nonumber\]
El electrodo de la derecha es el cátodo, donde se produce la reacción de reducción.
\[\mathrm{Ag}^{+}(a q)+e^{-} \rightleftharpoons \mathrm{Ag}(s) \nonumber\]
El potencial de la celda electroquímica en la Figura 11.2.1 es para la reacción
\[\mathrm{Zn}(s)+2 \mathrm{Ag}^{+}(a q) \rightleftharpoons 2 \mathrm{Ag}(s)+\mathrm{Zn}^{2+}(\mathrm{aq}) \nonumber\]
También definimos celdas electroquímicas potenciométricas de tal manera que el cátodo es el electrodo indicador y el ánodo es el electrodo de referencia.
La razón para separar los electrodos es evitar que la reacción de oxidación y la reacción de reducción ocurran en uno de los electrodos. Por ejemplo, si colocamos una tira de metal Zn en una solución de AgnO 3, la reducción de Ag + a Ag ocurre en la superficie del Zn al mismo tiempo que una poción del metal Zn se oxida a Zn 2 +. Debido a que la transferencia de electrones de Zn a Ag + ocurre en la superficie del electrodo, no podemos pasarlos a través del potenciómetro.
Notación abreviada para celdas electroquímicas
Aunque la Figura 11.2.1 proporciona una imagen útil de una celda electroquímica, no es una manera conveniente de representarla (¡Imagínese tener que dibujar una imagen de cada celda electroquímica que esté usando!). Una forma más útil de describir una celda electroquímica es una notación taquigráfica que utiliza símbolos para identificar diferentes fases y que enumera la composición de cada fase. Utilizamos una barra vertical (|) para identificar un límite entre dos fases donde se desarrolla un potencial, y una coma (,) para separar especies en la misma fase o para identificar un límite entre dos fases donde no se desarrolla potencial. Las notaciones de celdas cortas comienzan con el ánodo y continúan hacia el cátodo. Por ejemplo, describimos la celda electroquímica en la Figura 11.2.1 usando la siguiente notación abreviada.
\[\text{Zn}(s) | \text{ZnCl}_2(aq, a_{\text{Zn}^{2+}} = 0.0167) || \text{AgNO}_3(aq, a_{\text{Ag}^+} = 0.100) | \text{Ag} (s) \nonumber\]
La doble barra vertical (||) representa el puente de sal, cuyo contenido generalmente no enumeramos. Tenga en cuenta que una doble barra vertical implica que hay una diferencia de potencial entre el puente de sal y cada media celda.
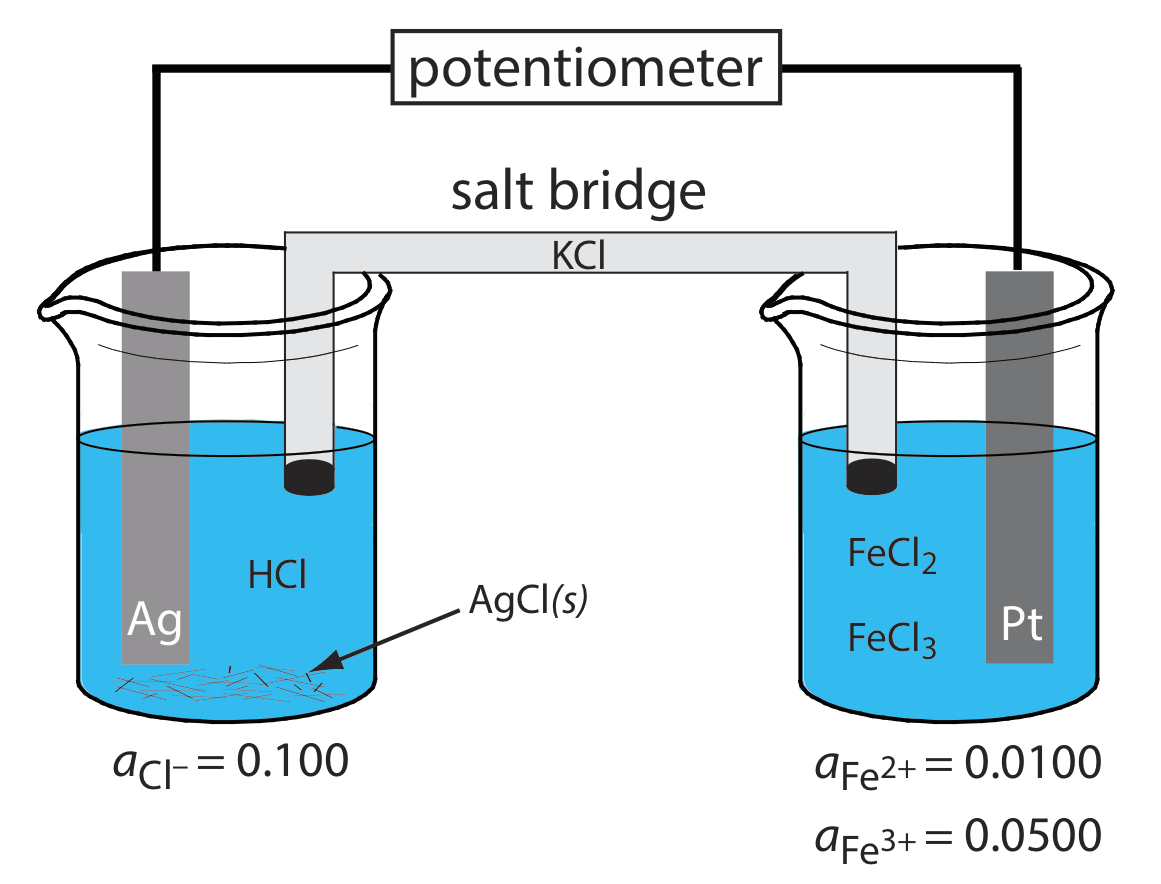
¿Cuáles son las reacciones anódicas, catódicas y globales responsables del potencial de la celda electroquímica en la Figura 11.2.2 ? Escriba la notación taquigráfica para la celda electroquímica.
Solución
La oxidación de Ag a Ag + ocurre en el ánodo, que es la semicelda izquierda. Debido a que la solución contiene una fuente de Cl, la reacción anódica es
\[\mathrm{Ag}(s)+\mathrm{Cl}^{-}(aq) \rightleftharpoons\text{ AgCl}(s)+e^{-} \nonumber\]
La reacción catódica, que es la semicelda derecha, es la reducción de Fe 3 + a Fe 2 +.
\[\mathrm{Fe}^{3+}(a q)+e^{-}\rightleftharpoons \text{ Fe}^{2+}(a q) \nonumber\]
La reacción celular global, por lo tanto, es
\[\mathrm{Ag}(s)+\text{ Fe}^{3+}(a q)+\text{ Cl}^{-}(a q) \rightleftharpoons \mathrm{AgCl}(s)+\text{ Fe}^{2+}(a q) \nonumber\]
La notación taquigráfica de la celda electroquímica es
\[\text{Ag}(s) | \text{HCl} (aq, a_{\text{Cl}^{-}} = 0.100), \text{AgCl} (\text{sat’d}) || \text{FeCl}_2(aq, a_{\text{Fe}^{2+}} = 0.0100), \text{ Fe}^{3+}(aq,a_{\text{Fe}^{3+}} = 0.0500) | \text{Pt} (s) \nonumber\]
Tenga en cuenta que el cátodo de Pt es un electrodo inerte que transporta electrones a la media reacción de reducción. El electrodo en sí no sufre reducción.
Escriba las reacciones que ocurren en el ánodo y el cátodo para la celda electroquímica potenciométrica con la siguiente notación taquigráfica.
Pt (s) | H 2 (g), H + (aq) || Cu 2 + (aq) | Cu (s)
- Responder
-
La oxidación de H 2 a H + ocurre en el ánodo
\[\mathrm{H}_{2}(g)\rightleftharpoons2 \mathrm{H}^{+}(a q)+2 e^{-} \nonumber\]
y la reducción de Cu 2 + a Cu ocurre en el cátodo.
\[\mathrm{Cu}^{2+}(a q)+2 e^{-}\rightleftharpoons\mathrm{Cu}(s) \nonumber\]
La reacción celular global, por lo tanto, es
\[\mathrm{Cu}^{2+}(a q)+\text{ H}_{2}(g)\rightleftharpoons2 \mathrm{H}^{+}(a q)+\mathrm{Cu}(s) \nonumber\]
Potencial y actividad: la ecuación de Nernst
El potencial de una celda electroquímica potenciométrica es
\[E_{\text {cell }}=E_{\text {cathode }}-E_{\text {anode }} \label{11.1}\]
donde el cátodo E y el ánodo E son potenciales de reducción para las reacciones redox en el cátodo y el ánodo, respectivamente. Cada potencial de reducción viene dado por la ecuación de Nernst
\[E=E^{\circ}-\frac{R T}{n F} \ln Q \nonumber\]
donde E o es el potencial de reducción de estado estándar, R es la constante de gas, T es la temperatura en Kelvins, n es el número de electrones en la reacción redox, F es la constante de Faraday y Q es el cociente de reacción. A una temperatura de 298 K (25 o C) la ecuación de Nernst es
\[E=E^{\circ}-\frac{0.05916}{n} \log Q \label{11.2}\]
donde E está en voltios.
Usando la Ecuación\ ref {11.2}, el potencial del ánodo y el cátodo en la Figura 11.2.1 son
\[E_\text{anode} = E_{\text{Zn}^{2+}/\text{Zn}}^{\circ} - \frac {0.05916} {2} \log \frac{1} {a_{\text{Zn}^{2+}}} \nonumber\]
\[E_\text{anode} = E_{\text{Ag}^{+}/\text{Ag}}^{\circ} - \frac {0.05916} {1} \log \frac{1} {a_{\text{Ag}^{+}}} \nonumber\]
A pesar de que se está produciendo una reacción de oxidación en el ánodo, definimos el potencial del ánodo en términos de la reacción de reducción correspondiente y el potencial de reducción en estado estándar. Consulte el Capítulo 6.4 para una revisión del uso de la ecuación de Nernst en los cálculos.
Sustituyendo el cátodo E y el ánodo E en la Ecuación\ ref {11.1}, junto con las actividades de Zn 2 + y Ag + y los potenciales de reducción de estado estándar, da celda E como
\[E_\text{cell} = \left( E_{\text{Ag}^{+}/\text{Ag}}^{\circ} - \frac {0.05916} {1} \log \frac{1} {a_{\text{Ag}^{+}}} \right) - \left( E_{\text{Zn}^{2+}/\text{Zn}}^{\circ} - \frac {0.05916} {2} \log \frac{1} {a_{\text{Zn}^{2+}}} \right) \nonumber\]
\[E_\text{cell} = \left( 0.7996 - \frac {0.05916} {1} \log \frac{1} {0.100} \right) - \left( -0.7618 - \frac {0.05916} {2} \log \frac{1} {0.0167} \right) = 1.555 \text{ V} \nonumber\]
Encontrará valores para los potenciales de reducción de estado estándar en el Apéndice 13.
¿Cuál es el potencial de la celda electroquímica que se muestra en el Ejemplo 11.2.1 ?
Solución
Sustituir el cátodo E y el ánodo E en la ecuación\ ref {11.1}, junto con las concentraciones de Fe 3 +, Fe 2+ y Cl, y los potenciales de reducción de estado estándar da
\[E_\text{cell} = \left( E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} - \frac {0.05916} {1} \log \frac{a_{\text{Fe}^{2+}}} {a_{\text{Fe}^{3+}}} \right) - \left( E_{\text{AgCl/Ag}}^{\circ} - \frac {0.05916} {1} \log a_{\text{Cl}^-} \right) \nonumber\]
\[E_\text{cell} = \left( 0.771 - \frac {0.05916} {1} \log \frac{0.0100} {0.0500} \right) - \left( 0.2223 - \frac {0.05916} {1} \log (0.100) \right) = 0.531 \text{ V} \nonumber\]
¿Cuál es el potencial de la celda electroquímica en el Ejercicio 11.2.1 si la actividad de H + en la semicelda anódica es 0.100, la fugacidad de H 2 en la semicelda anódica es 0.500, y la actividad de Cu 2 + en la mitad catódica- celular es 0.0500? Fugacidad,\(f\), es el término equivalente para la actividad de un gas.
- Responder
-
Hacer sustituciones apropiadas en la Ecuación\ ref {11.1} y resolver para la celda E da su valor como
\[E_\text{cell} = \left( E_{\text{Cu}^{2+}/\text{Cu}}^{\circ} - \frac {0.05916} {2} \log \frac{1} {a_{\text{Cu}^{2+}}} \right) - \left( E_{\text{H}^{+}/\text{H}_2}^{\circ} - \frac {0.05916} {2} \log \frac{f_{\text{H}_2}} {a_{\text{H}^+}^2} \right) \nonumber\]
\[E_\text{cell} = \left( 0.3419 - \frac {0.05916} {2} \log \frac{1} {0.0500} \right) - \left( 0.0000 - \frac {0.05916} {2} \log \frac{0.500} {(0.100)^2} \right) = 0.3537 \text{ V} \nonumber\]
En potenciometría, asignamos el electrodo de referencia a la semicelda anódica y asignamos el electrodo indicador a la semicelda catódica. Así, si el potencial de la celda en la Figura 11.2.1 es +1.50 V y la actividad de Zn 2 + es 0.0167, entonces podemos resolver la siguiente ecuación para un Ag +
\[1.50 \text{ V} = \left( 0.7996 - \frac {0.05916} {1} \log \frac{1} {a_{\text{Ag}^+}} \right) - \left( -0.7618 - \frac {0.05916} {2} \log \frac{1} {0.0167} \right) \nonumber\]
obteniendo una actividad de 0.0118.
Cuál es la actividad de Fe 3 + en una celda electroquímica similar a la del Ejemplo 11.2.1 si la actividad de Cl — en la celda izquierda es 1.0, la actividad de Fe 2 + en la celda derecha es 0.015, y E la celda es +0.546 V?
Solución
Hacer sustituciones apropiadas en la Ecuación\ ref {11.1}
\[0.546 = \left( 0.771 - \frac {0.05916} {1} \log \frac{0.0100} {a_{\text{Fe}^{3+}}} \right) - \left( 0.2223 - \frac {0.05916} {1} \log (1.0) \right) \nonumber\]
y resolviendo para un Fe 3 + da su actividad como 0.0135.
¿Cuál es la actividad de Cu 2 + en la celda electroquímica en el Ejercicio 11.2.1 si la actividad de H + en la semicelda anódica es 1.00 con una fugacidad de 1.00 para H 2, y una celda E de +0.257 V?
- Responder
-
Hacer sustituciones apropiadas en la Ecuación\ ref {11.1}
\[0.257 \text{ V} = \left( 0.3419 - \frac {0.05916} {2} \log \frac{1} {a_{\text{Cu}^{2+}}} \right) - \left( 0.0000 - \frac {0.05916} {2} \log \frac{1.00} {(1.00)^2} \right) \nonumber\]
y resolviendo para un Cu 2 + da su actividad como\(1.35 \times 10^{-3}\).
A pesar de la aparente facilidad de determinar la actividad de un analito usando la ecuación de Nernst, existen varios problemas con este enfoque. Un problema es que los potenciales de estado estándar dependen de la temperatura y los valores en las tablas de referencia suelen ser para una temperatura de 25 o C. Podemos superar este problema manteniendo la celda electroquímica a 25 o C o midiendo el potencial de estado estándar en el deseado temperatura.
Otro problema es que un potencial de reducción de estado estándar puede tener un efecto matricial significativo. Por ejemplo, el potencial de reducción en estado estándar para el par redox Fe 3 + /Fe 2+ es +0.735 V en HCl 1 M, +0.70 V en HCl 1 M y +0.53 V en HCl 10 M. La diferencia de potencial para soluciones equimolares de HCl y HClO 4 es el resultado de una diferencia en los coeficientes de actividad para Fe 3 + y Fe 2 + en estos dos medios. El cambio hacia un potencial más negativo con un aumento en la concentración de HCl es el resultado de la capacidad del cloruro para formar un complejo más fuerte con Fe 3 + que con Fe 2 +. Podemos minimizar este problema reemplazando el potencial de estado estándar por un potencial formal dependiente de la matriz. La mayoría de las tablas de potenciales de estado estándar, incluidos los del Apéndice 13, incluyen potenciales formales seleccionados.
Finalmente, un problema más grave es la presencia de potenciales adicionales en la celda electroquímica no incluidos en la Ecuación\ ref {11.1}. Al escribir la notación taquigráfica para una celda electroquímica usamos una doble barra (||) para indicar el puente salino, sugiriendo que existe un potencial en la interfaz entre cada extremo del puente salino y la solución en la que se sumerge. El origen de este potencial se discute en la siguiente sección.
Potenciales de unión
Se desarrolla un potencial de unión en la interfaz entre dos soluciones iónicas si hay una diferencia en la concentración y movilidad de los iones. Consideremos, por ejemplo, una membrana porosa que separe una solución de HCl 0.1 M de una solución de HCl 0.01 M (Figura 11.2.3 a). Debido a que la concentración de HCl en el lado izquierdo de la membrana es mayor que la del lado derecho de la membrana, H + y Cl — se difundirán en la dirección de las flechas. La movilidad de H +, sin embargo, es mayor que la de Cl —, como lo demuestra la diferencia en las longitudes de sus respectivas flechas. Debido a esta diferencia de movilidad, la solución en el lado derecho de la membrana desarrolla un exceso de concentración de H + y una carga positiva (Figura 11.2.3 b). Simultáneamente, la solución en el lado izquierdo de la membrana desarrolla una carga negativa debido a que hay un exceso de concentración de Cl —. Llamamos a esta diferencia de potencial a través de la membrana un potencial de unión y la representamos como E j.
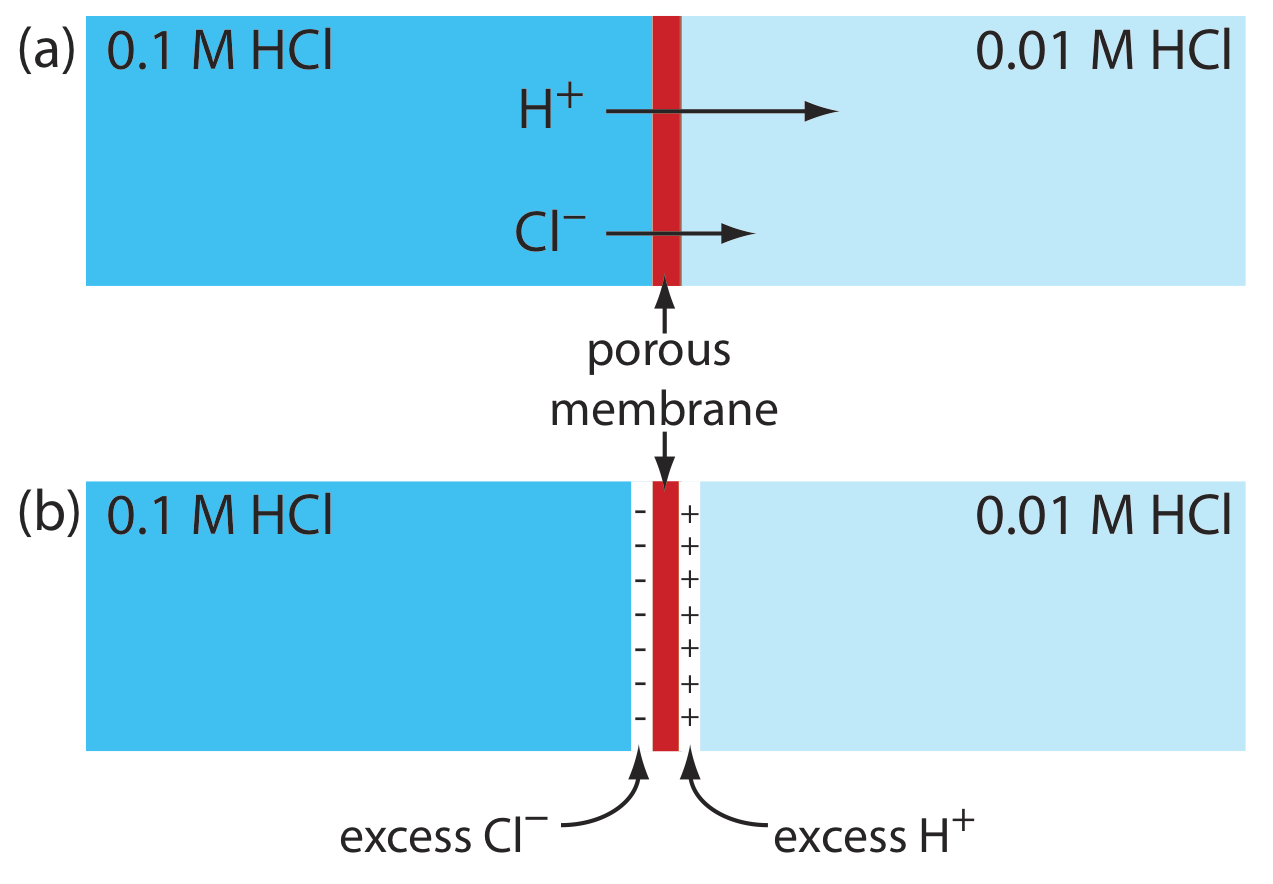
La magnitud del potencial de unión depende de la diferencia en la concentración de iones en los dos lados de la interfaz, y puede ser tan grande como 30—40 mV. Por ejemplo, se ha medido un potencial de unión de 33.09 mV en la interfaz entre soluciones de HCl 0.1 M y NaCl 0.1 M [Sawyer, D. T.; Roberts, J. L., Jr. Electroquímica experimental para químicos, Wiley-Interscience: Nueva York, 1974, p. 22]. El potencial de unión de un puente salino se minimiza mediante el uso de una sal, como KCl, para la cual las movilidades del catión y anión son aproximadamente iguales. También podemos minimizar el potencial de unión incorporando una alta concentración de sal en el puente salino. Por esta razón, los puentes salinos se construyen frecuentemente usando soluciones que están saturadas con KCl. Sin embargo, siempre está presente un pequeño potencial de unión, generalmente de magnitud desconocida.
Cuando medimos el potencial de una celda electroquímica, el potencial de unión también contribuye a la celda E; así, reescribimos la Ecuación\ ref {11.1} como
\[E_{\text {cell }}=E_{\text {cathode }}-E_{\text {anode }}+E_{j} \nonumber\]
para incluir su contribución. Si no conocemos el valor real del potencial de unión, que es la situación habitual, entonces no podemos calcular directamente la concentración del analito usando la ecuación de Nernst. Sin embargo, el trabajo analítico cuantitativo es posible si utilizamos uno de los métodos de estandarización —estándares externos, método de adiciones estándar o estándares internos— discutidos en el Capítulo 5.3.
Electrodos de Referencia
En una celda electroquímica potenciométrica una de las dos medias celdas proporciona un potencial de referencia fijo y el potencial de la otra semicelda responde a la concentración del analito. Por convención, el electrodo de referencia es el ánodo; así, la notación manual corta para una celda electroquímica potenciométrica es
electrodo de referencia || electrodo indicador
y el potencial celular es
\[E_{\mathrm{cell}}=E_{\mathrm{ind}}-E_{\mathrm{ref}}+E_{j} \nonumber\]
El electrodo de referencia ideal proporciona un potencial estable y conocido para que podamos atribuir cualquier cambio en la celda E al efecto del analito sobre el potencial del electrodo indicador. Además, debe ser fácil de hacer y usar el electrodo de referencia. En esta sección se discuten tres electrodos de referencia comunes.
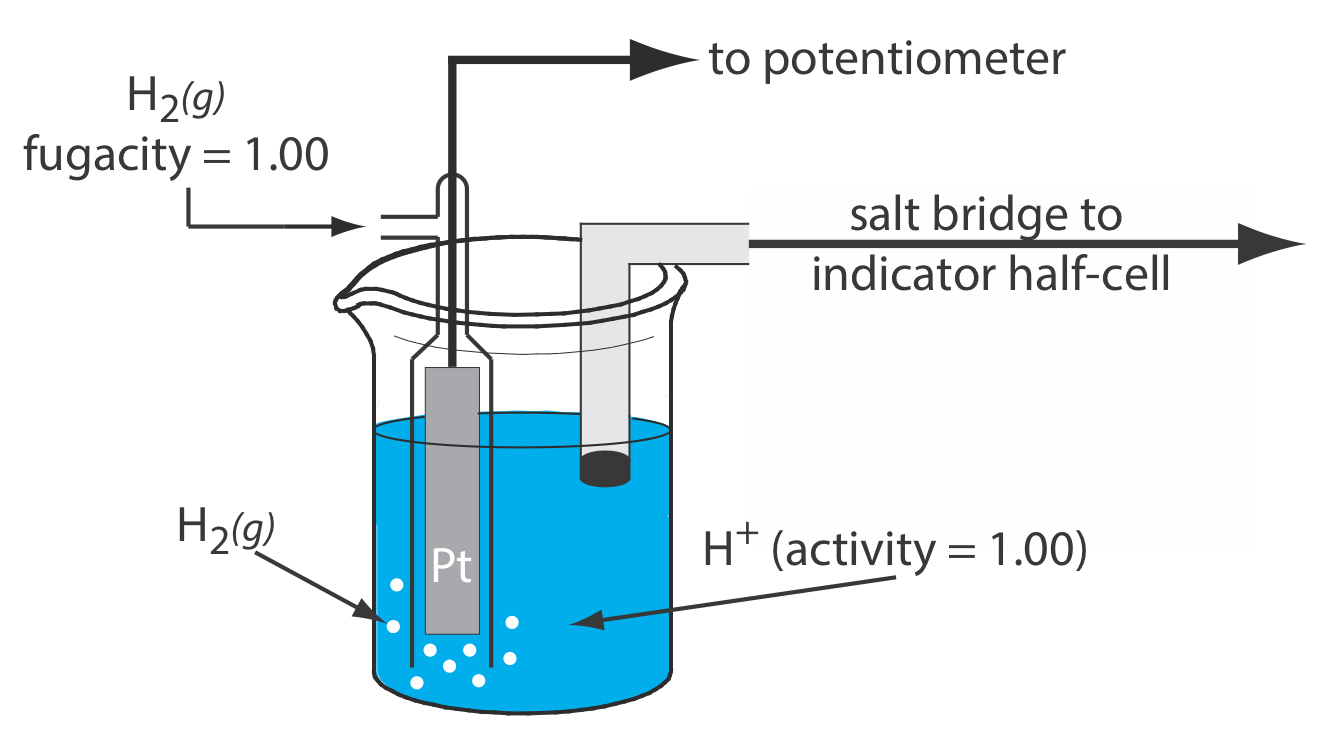
Electrodo de Hidrógeno Estándar
Aunque rara vez usamos el electrodo de hidrógeno estándar (SHE) para el trabajo analítico de rutina, es el electrodo de referencia utilizado para establecer potenciales de estado estándar para otras medias reacciones. El SHE consiste en un electrodo de Pt sumergido en una solución en la que la actividad del ion hidrógeno es 1.00 y en la que la fugacidad de H 2 (g) es 1.00 (Figura 11.2.4 ). Un puente salino convencional conecta la SHE a la semicelda indicadora. La notación de mano corta para el electrodo de hidrógeno estándar es
\[\text{Pt}(s), \text{ H}_{2}\left(g, f_{\mathrm{H}_{2}}=1.00\right) | \text{ H}^{+}\left(a q, a_{\mathrm{H}^{+}}=1.00\right) \| \nonumber\]
y el potencial de estado estándar para la reacción
\[\mathrm{H}^{+}(a q)+e^{-}=\frac{1}{2} \mathrm{H}_{2}(g) \nonumber\]
es, por definición, 0.00 V a todas las temperaturas. A pesar de su importancia como electrodo de referencia fundamental contra el que medimos todos los demás potenciales, rara vez se usa la SHE porque es difícil de preparar e inconveniente de usar.
Electrodos de Calomelanos
Un electrodo de referencia de calomelanos se basa en el siguiente par redox entre Hg 2 Cl 2 y Hg (calomel es el nombre común para Hg 2 Cl 2)
\[\mathrm{Hg}_{2} \mathrm{Cl}_{2}(s)+2 e^{-}\rightleftharpoons2 \mathrm{Hg}(l)+2 \mathrm{Cl}^{-}(a q) \nonumber\]
para lo cual el potencial es
\[E=E_{\mathrm{Hg}_{2} \mathrm{Cl}_{2} / \mathrm{Hg}}^{\mathrm{o}}-\frac{0.05916}{2} \log \left(a_{\text{Cl}^-}\right)^{2}=+0.2682 \mathrm{V}-\frac{0.05916}{2} \log \left(a_{\text{Cl}^-}\right)^{2} \nonumber\]
El potencial de un electrodo de calomelanos, por lo tanto, depende de la actividad de Cl —en equilibrio con Hg y Hg 2 Cl 2.
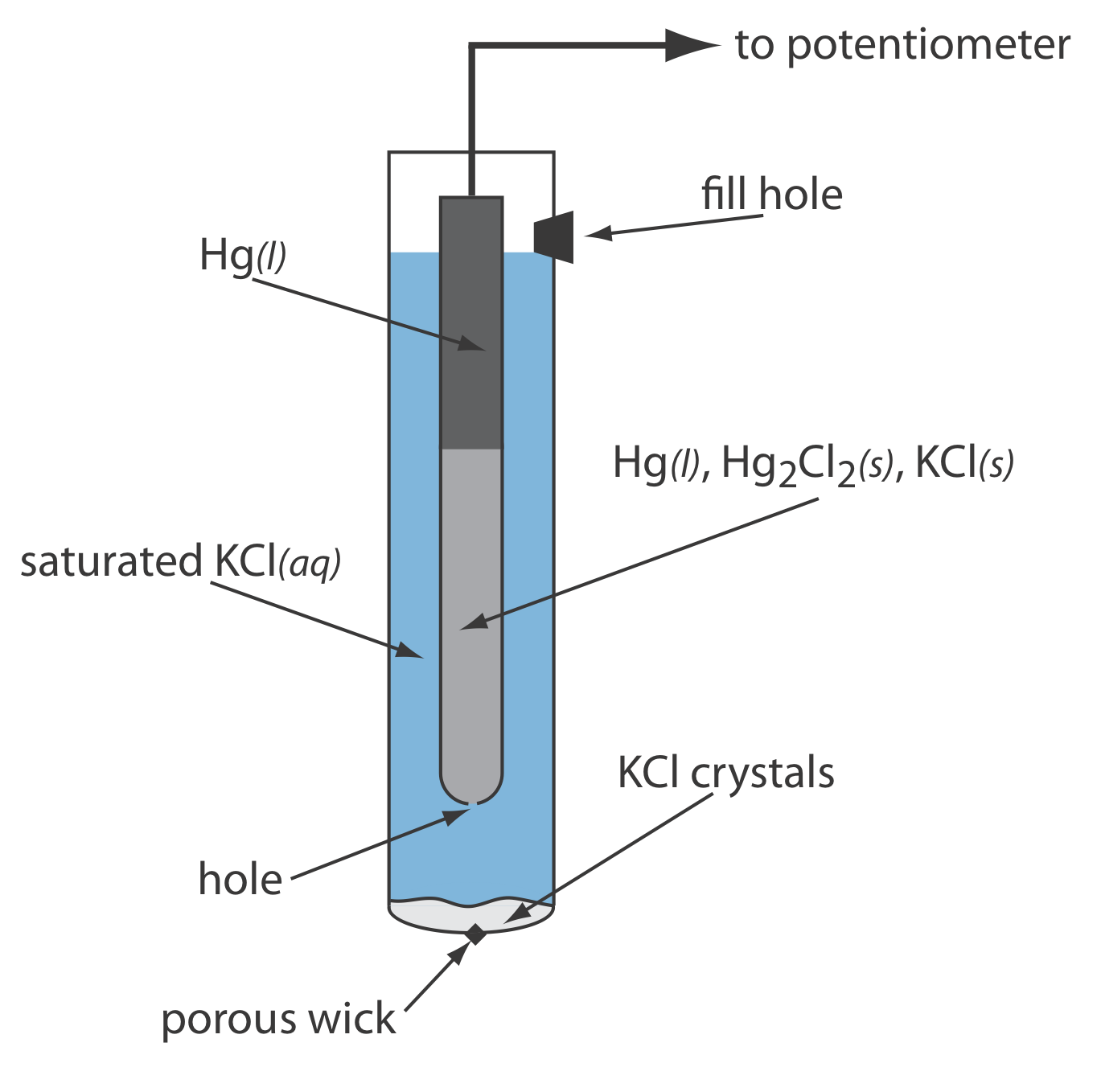
Como se muestra en la Figura 11.2.5 , en un electrodo de calomelanos saturado (SCE) la concentración de Cl — está determinada por la solubilidad de KCl. El electrodo consiste en un tubo interno empaquetado con una pasta de Hg, Hg 2 Cl 2 y KCl, situado dentro de un segundo tubo que contiene una solución saturada de KCl. Un pequeño orificio conecta los dos tubos y una mecha porosa sirve como puente salino a la solución en la que se sumerge el SCE. Un tapón en el tubo exterior proporciona una abertura para agregar KCl saturado de adición. La notación de mano corta para esta celda es
\[\mathrm{Hg}(l) | \mathrm{Hg}_{2} \mathrm{Cl}_{2}(s), \mathrm{KCl}(a q, \text { sat'd }) \| \nonumber\]
Debido a que la concentración de Cl — se fija por la solubilidad de KCl, el potencial de un SCE permanece constante aunque perdamos parte de la solución interna por evaporación. Una desventaja significativa del SCE es que la solubilidad del KCl es sensible a un cambio de temperatura. A temperaturas más altas la solubilidad de KCl aumenta y el potencial del electrodo disminuye. Por ejemplo, el potencial del SCE es +0.2444 V a 25 o C y +0.2376 V a 35 o C. El potencial de un electrodo de calomelanos que contiene una solución insaturada de KCl es menos dependiente de la temperatura, pero su potencial cambia si la concentración, y por lo tanto la actividad de Cl —, aumenta debido a la evaporación.
Por ejemplo, el potencial de un electrodo de calomelanos es +0.280 V cuando la concentración de KCl es 1.00 M y +0.336 V cuando la concentración de KCl es 0.100 M. Si la actividad de Cl — es 1.00, el potencial es +0.2682 V.
Electrodos de Plata/Cloruro de Plata
Otro electrodo de referencia común es el electrodo de plata/cloruro de plata, que se basa en la reducción de AgCl a Ag.
\[\operatorname{AgCl}(s)+e^{-} \rightleftharpoons \mathrm{Ag}(s)+\mathrm{Cl}^{-}(a q) \nonumber\]
Como es el caso del electrodo de calomelanos, la actividad de Cl — determina el potencial del electrodo de Ag/AgCl; así
\[E = E_\text{AgCl/Ag}^{\circ}-0.05916 \log a_{\text{Cl}^-} = 0.2223 \text{ V} - 0.05916 \log a_{\text{Cl}^-} \nonumber\]
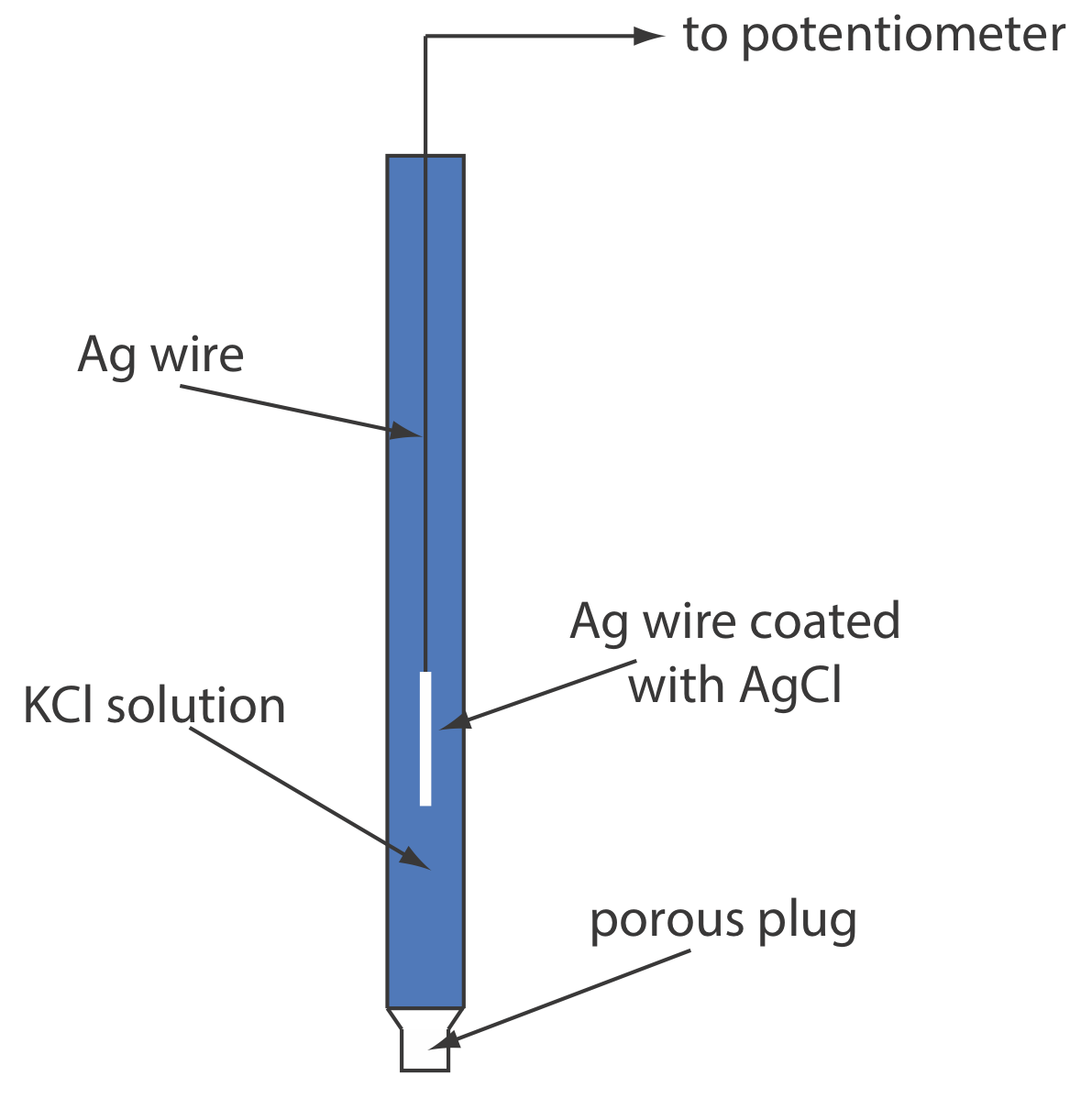
Cuando se prepara usando una solución saturada de KCl, el potencial del electrodo es +0.197 V a 25 o C. Otro electrodo común de Ag/AgCl utiliza una solución de KCl 3.5 M y tiene un potencial de +0.205 V a 25 o C. Como es de esperar, el potencial de un electrodo de Ag/AgCl usando una solución saturada de El KCl es más sensible a un cambio de temperatura que un electrodo que utiliza una solución insaturada de KCl.
Un electrodo típico de Ag/AgCl se muestra en la Figura 11.2.6 y consiste en un alambre de plata, cuyo extremo está recubierto con una película delgada de AgCl, sumergida en una solución que contiene la concentración deseada de KCl. Un tapón poroso sirve como puente de sal. La notación de mano corta del electrodo es
\[\operatorname{Ag}(s) | \operatorname{Ag} \mathrm{Cl}(s), \mathrm{KCl}\left(a q, a_{\mathrm{Cl}^{-}}=x\right) \| \nonumber\]
Conversión de potenciales entre electrodos de referencia
Los potenciales de reducción de estado estándar en la mayoría de las tablas se reportan en relación con el potencial del electrodo de hidrógeno estándar de +0.00 V. Debido a que rara vez usamos el SHE como electrodo de referencia, necesitamos convertir el potencial de un electrodo indicador a su valor equivalente cuando se usa un electrodo de referencia diferente. Como se muestra en el siguiente ejemplo, esto es fácil de hacer.
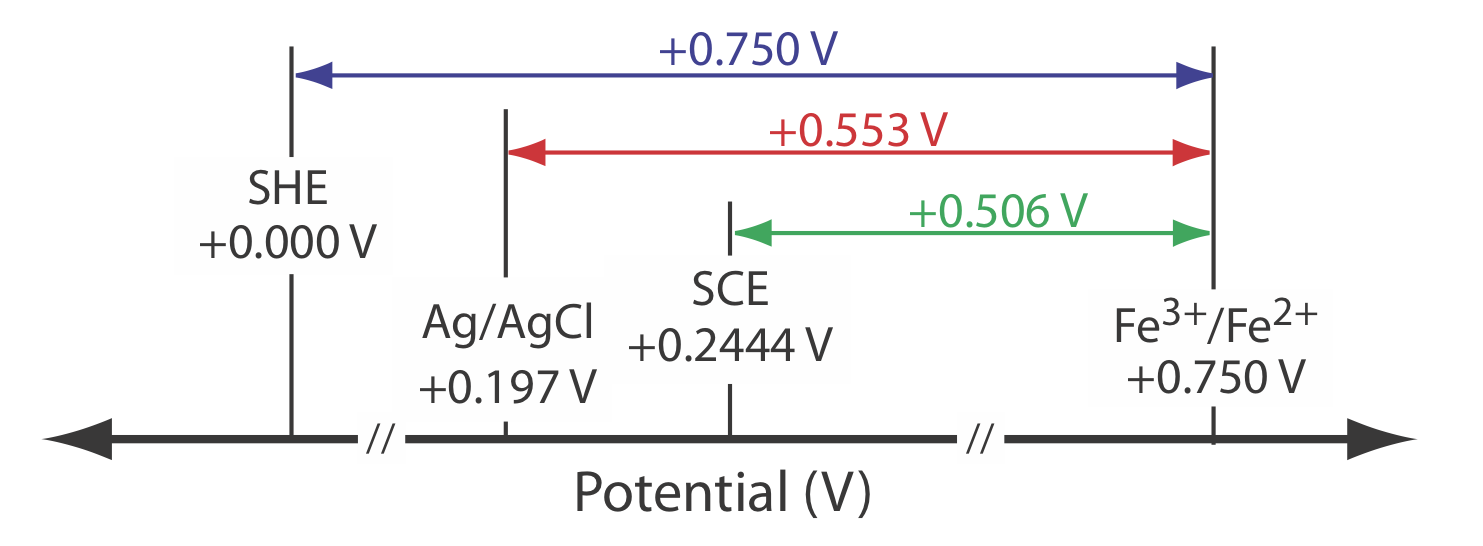
El potencial para una semicelda Fe 3 + /Fe 2+ es +0.750 V en relación con el electrodo de hidrógeno estándar. ¿Cuál es su potencial si usamos un electrodo de calomelano saturado o un electrodo saturado de plata/cloruro de plata?
Solución
Cuando usamos un electrodo de hidrógeno estándar, el potencial de la celda electroquímica es
\[E_\text{cell} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}} - E_\text{SHE} = 0.750 \text{ V} -0.000 \text{ V} = 0.750 \text{ V} \nonumber\]
Podemos usar la misma ecuación para calcular el potencial si usamos un electrodo de calomelano saturado
\[E_\text{cell} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}} - E_\text{SHE} = 0.750 \text{ V} -0.2444 \text{ V} = 0.506 \text{ V} \nonumber\]
o un electrodo saturado de plata/cloruro de plata
\[E_\text{cell} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}} - E_\text{SHE} = 0.750 \text{ V} -0.197 \text{ V} = 0.553 \text{ V} \nonumber\]
La Figura 11.2.7 proporciona una representación pictórica de la relación entre estos diferentes potenciales.
El potencial de una media celda\(\text{UO}_2^+\) /U 4+ es —0.0190 V en relación con un electrodo de calomelano saturado. ¿Cuál es su potencial cuando se usa un electrodo saturado de plata/cloruro de plata o un electrodo de hidrógeno estándar?
- Responder
-
Cuando se usa un electrodo de calomelano saturado, el potencial de la celda electroquímica es
\[E_\text{cell} = E_{\text{UO}_2^+/\text{U}^{4+}} - E_\text{SCE} \nonumber\]
Sustituir en valores conocidos
\[-0.0190 \text{ V} = E_{\text{UO}_2^+/\text{U}^{4+}} - 0.2444 \text{ V} \nonumber\]
y resolviendo para\(E_{\text{UO}_2^+/\text{U}^{4+}}\) da su valor como +0.2254 V. El potencial relativo al electrodo de Ag/AgCl es
\[E_\text{cell} = E_{\text{UO}_2^+/\text{U}^{4+}} - E_\text{Ag/AgCl} = 0.2254 \text{ V} - 0.197 \text{ V} = 0.028 \text{ V} \nonumber\]
y el potencial relativo al electrodo de hidrógeno estándar es
\[E_\text{cell} = E_{\text{UO}_2^+/\text{U}^{4+}} - E_\text{SHE} = 0.2254 \text{ V} - 0.000 \text{ V} = 0.2254 \text{ V} \nonumber\]
Electrodos indicadores metálicos
En potenciometría, el potencial del electrodo indicador es proporcional a la actividad del analito. Se utilizan dos clases de electrodos indicadores para realizar mediciones potenciométricas: electrodos metálicos, que son objeto de esta sección, y electrodos selectivos de iones, los cuales se cubren en la siguiente sección.
Electrodos de Primera Clase
Si colocamos un electrodo de cobre en una solución que contiene Cu 2 +, el potencial del electrodo debido a la reacción
\[\mathrm{Cu}^{2+}(a q)+2 e^{-} \rightleftharpoons \mathrm{Cu}(s) \nonumber\]
se determina por la actividad de Cu 2 +.
\[E=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\mathrm{o}}-\frac{0.05916}{2} \log \frac{1}{a_{\mathrm{Cu}^{2+}}}=+0.3419 \mathrm{V}-\frac{0.05916}{2} \log \frac{1}{a_{\mathrm{Cu}^{2+}}} \nonumber\]
Si el cobre es el electrodo indicador en una celda electroquímica potenciométrica que también incluye un electrodo de referencia de calomelanos saturado
\[\mathrm{SCE} \| \mathrm{Cu}^{2+}\left(a q, a_{\mathrm{Cu^{2+}}}=x\right) | \text{Cu}(s) \nonumber\]
entonces podemos usar el potencial celular para determinar una actividad desconocida de Cu 2 + en la semicelda del electrodo indicador
\[E_{\text{cell}}= E_{\text { ind }}-E_{\text {SCE }}+E_{j}= +0.3419 \mathrm{V}-\frac{0.05916}{2} \log \frac{1}{a_{\mathrm{Cu}^{2+}}}-0.2224 \mathrm{V}+E_{j} \nonumber\]
Un electrodo indicador en el que el metal está en contacto con una solución que contiene su ion se denomina electrodo de primer tipo. En general, si un metal, M, está en una solución de Mn+, el potencial celular es
\[E_{\mathrm{call}}=K-\frac{0.05916}{n} \log \frac{1}{a_{M^{n+}}}=K+\frac{0.05916}{n} \log a_{M^{n+}} \nonumber\]
donde K es una constante que incluye el potencial de estado estándar para el par redox Mn+/M, el potencial del electrodo de referencia y el potencial de unión.
Tenga en cuenta que incluyendo E j en la constante K significa que no necesitamos conocer el valor real del potencial de unión; sin embargo, el potencial de unión debe permanecer constante si K es para mantener un valor constante.
Por una variedad de razones, incluyendo la cinética lenta de transferencia de electrones en la interfaz metal—solución, la formación de óxidos metálicos en la superficie del electrodo y las reacciones interferentes, los electrodos del primer tipo se limitan a los siguientes metales: Ag, Bi, Cd, Cu, Hg, Pb, Sn, Tl y Zn.
Muchos de estos electrodos, como el Zn, no pueden ser utilizados en soluciones ácidas porque son fácilmente oxidados por H +.
\[\mathrm{Zn}(s)+2 \mathrm{H}^{+}(a q)\rightleftharpoons \text{ H}_{2}(g)+\mathrm{Zn}^{2+}(a q) \nonumber\]
Electrodos de la Segunda Clase
El potencial de un electrodo de primer tipo responde a la actividad de M n +. También podemos utilizar este electrodo para determinar la actividad de otra especie si está en equilibrio con M n +. Por ejemplo, el potencial de un electrodo de Ag en una solución de Ag + es
\[E=0.7996 \mathrm{V}+0.05916 \log a_{\mathrm{Ag}^{+}} \label{11.3}\]
Si saturamos la semicelda del electrodo indicador con AGi, la reacción de solubilidad
\[\operatorname{Agl}(s)\rightleftharpoons\operatorname{Ag}^{+}(a q)+\mathrm{I}^{-}(a q) \nonumber\]
determina la concentración de Ag +; así
\[a_{\mathrm{Ag}^{+}}=\frac{K_{\mathrm{sp}, \mathrm{Agl}}}{a_{\text{I}^-}} \label{11.4}\]
donde K sp, AGi es el producto de solubilidad para AGi. Sustituyendo la ecuación\ ref {11.4} en la ecuación\ ref {11.3}
\[E=0.7996 \text{ V}+0.05916 \log \frac{K_{\text{sp, Agl}}}{a_{\text{I}^-}} \nonumber\]
muestra que el potencial del electrodo de plata es una función de la actividad de I —. Si incorporamos este electrodo en una celda electroquímica potenciométrica con un electrodo de calomelano saturado
\[\mathrm{SCE} \| \mathrm{AgI}(s), \text{ I}^-\left(a q, a_{\text{I}^-}=x\right) | \mathrm{Ag}(\mathrm{s}) \nonumber\]
entonces el potencial celular es
\[E_{\mathrm{cell}}=K-0.05916 \log a_{\text{I}^-} \nonumber\]
donde K es una constante que incluye el potencial de estado estándar para el par redox Ag + /Ag, el producto de solubilidad para AGi, el potencial del electrodo de referencia y el potencial de unión.
Si un electrodo de primer tipo responde a la actividad de un ion en equilibrio con M n +, lo llamamos electrodo de segundo tipo. Dos electrodos comunes del segundo tipo son el calomel y los electrodos de referencia plata/cloruro de plata.
En un electrodo del segundo tipo enlazamos una reacción redox y otra reacción, como una reacción de solubilidad. Quizás te preguntes si podemos vincular más de dos reacciones. La respuesta corta es sí. Un electrodo de tercer tipo, por ejemplo, une una reacción redox y otras dos reacciones. Dichos electrodos son menos comunes y no los consideraremos en este texto.
Electrodos Redox
Un electrodo del primer tipo o segundo tipo desarrolla un potencial como resultado de una reacción redox que involucra al electrodo metálico. Un electrodo también puede servir como fuente de electrones o como sumidero de electrones en una reacción redox no relacionada, en cuyo caso lo llamamos electrodo redox. El cátodo Pt en la Figura 11.2.2 y Ejemplo 11.2.1 es un electrodo redox porque su potencial está determinado por la actividad de Fe 2 + y Fe 3 + en la semicelda indicadora. Tenga en cuenta que el potencial de un electrodo redox a menudo responde a la actividad de más de un ion, lo que limita su utilidad para la potenciometría directa.
Electrodos de membrana
Si los metales fueran los únicos materiales útiles para construir electrodos indicadores, entonces habría pocas aplicaciones útiles de potenciometría. En 1906, Cremer descubrió que la diferencia de potencial a través de una fina membrana de vidrio es una función del pH cuando lados opuestos de la membrana están en contacto con soluciones que tienen diferentes concentraciones de H 3 O +. La existencia de este potencial de membrana condujo al desarrollo de una nueva clase de electrodos indicadores, a los que llamamos electrodos selectivos de iones (ISE). Además del electrodo de pH de vidrio, los electrodos selectivos de iones están disponibles para una amplia gama de iones. También es posible construir un electrodo de membrana para un analito neutro mediante el uso de una reacción química para generar un ion que se monitoriza con un electrodo selectivo de iones. El desarrollo de nuevos electrodos de membrana continúa siendo un área activa de investigación.
Potenciales de Membrana
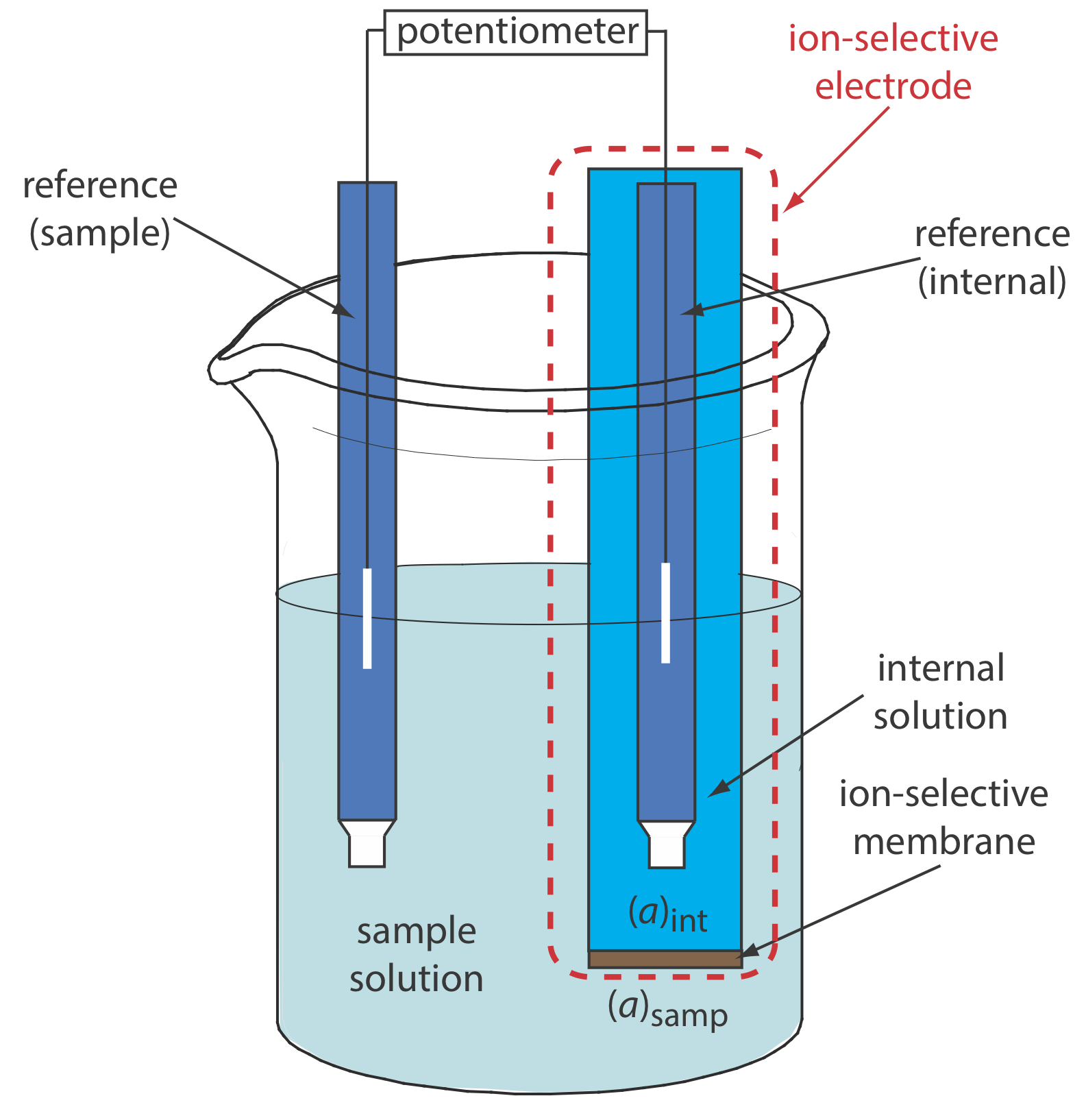
La Figura 11.2.8 muestra una celda electroquímica potenciométrica típica equipada con un electrodo selectivo de iones. La notación de mano corta para esta celda es
\[\text { ref (sample) }\left\|[\mathrm{A}]_{\text { samp }}\left(a q, a_{\mathrm{A}}=x\right) |[\mathrm{A}]_{\text { int }}\left(a q, a_{\mathrm{A}}=y\right)\right\| \text { ref (internal) } \nonumber\]
donde la membrana selectiva de iones está representada por la barra vertical que separa las dos soluciones que contienen analito: la solución de muestra y la solución interna del electrodo selectivo de iones. El potencial de esta celda electroquímica incluye el potencial de cada electrodo de referencia, un potencial de unión y el potencial de la membrana
\[E_\text{cell} = E_\text{ref(int)} - E_\text{ref(samp)} + E_\text{mem} + E_j \label{11.5}\]
donde E mem es el potencial a través de la membrana y Las notaciones ref (muestra) y ref (interna) representan un electrodo de referencia sumergido en la muestra y un electrodo de referencia sumergido en la solución interna del ISE. Debido a que el potencial de unión y el potencial de los dos electrodos de referencia son constantes, cualquier cambio en la celda E refleja un cambio en el potencial de la membrana.
La interacción del analito con la membrana genera un potencial de membrana si hay una diferencia en su actividad en los dos lados de la membrana. La corriente es transportada a través de la membrana por el movimiento del analito o de un ion ya presente en la matriz de la membrana. El potencial de membrana viene dado por la siguiente ecuación similar a Nernst
donde (a) samp es la actividad del analito en la muestra, (a) int es la actividad del analito en la solución interna del electrodo selectivo de iones, y z es la carga del analito. Idealmente, E mem es cero cuando (a A) int = (a A) samp. El término E asym, que es un potencial de asimetría, explica el hecho de que E mem generalmente no es cero bajo estas condiciones.
Por ahora simplemente notamos que una diferencia en la actividad del analito da como resultado un potencial de membrana. Al considerar diferentes tipos de electrodos selectivos de iones, exploraremos más específicamente la fuente del potencial de membrana.
Sustituyendo la Ecuación\ ref {11.6} en la Ecuación\ ref {11.5}, asumiendo una temperatura de 25 o C, y reordenando da
\[E_{\mathrm{cell}}=K+\frac{0.05916}{z} \log \left(a_{A}\right)_{\mathrm{samp}} \label{11.7}\]
donde K es una constante que incluye los potenciales de los dos electrodos de referencia, los potenciales de unión, el potencial de asimetría y la actividad del analito en la solución interna. La ecuación\ ref {11.7} es una ecuación general y se aplica a todos los tipos de electrodos selectivos de iones.
Selectividad de Membranas
Un potencial de membrana es el resultado de una interacción química entre el analito y los sitios activos en la superficie de la membrana. Debido a que la señal depende de un proceso químico, la mayoría de las membranas no son selectivas hacia un solo analito. En cambio, el potencial de membrana es proporcional a la concentración de cada ion que interactúa con los sitios activos de la membrana. Podemos reescribir la Ecuación\ ref {11.7} para incluir la contribución al potencial de un interferente, I
\[E_\text{cell} = K + \frac {0.05916} {z_A} \log \left\{ a_A + K_{A,I}(a_I)^{z_A/z_I} \right\} \nonumber\]
donde z A y z I son las cargas del analito y el interferente, y K A, I es un coeficiente de selectividad que da cuenta de la respuesta relativa del interferente. El coeficiente de selectividad se define como
\[K_{A,I} = \frac {(a_A)_e} {(a_I)_e^{z_A/z_I}} \label{11.8}\]
donde (a) e y (a I) e son las actividades del analito y el interferente que producen potenciales celulares idénticos. Cuando el coeficiente de selectividad es 1.00, la membrana responde por igual al analito y al interferente. Una membrana muestra buena selectividad para el analito cuando K A, I es significativamente menor a 1.00.
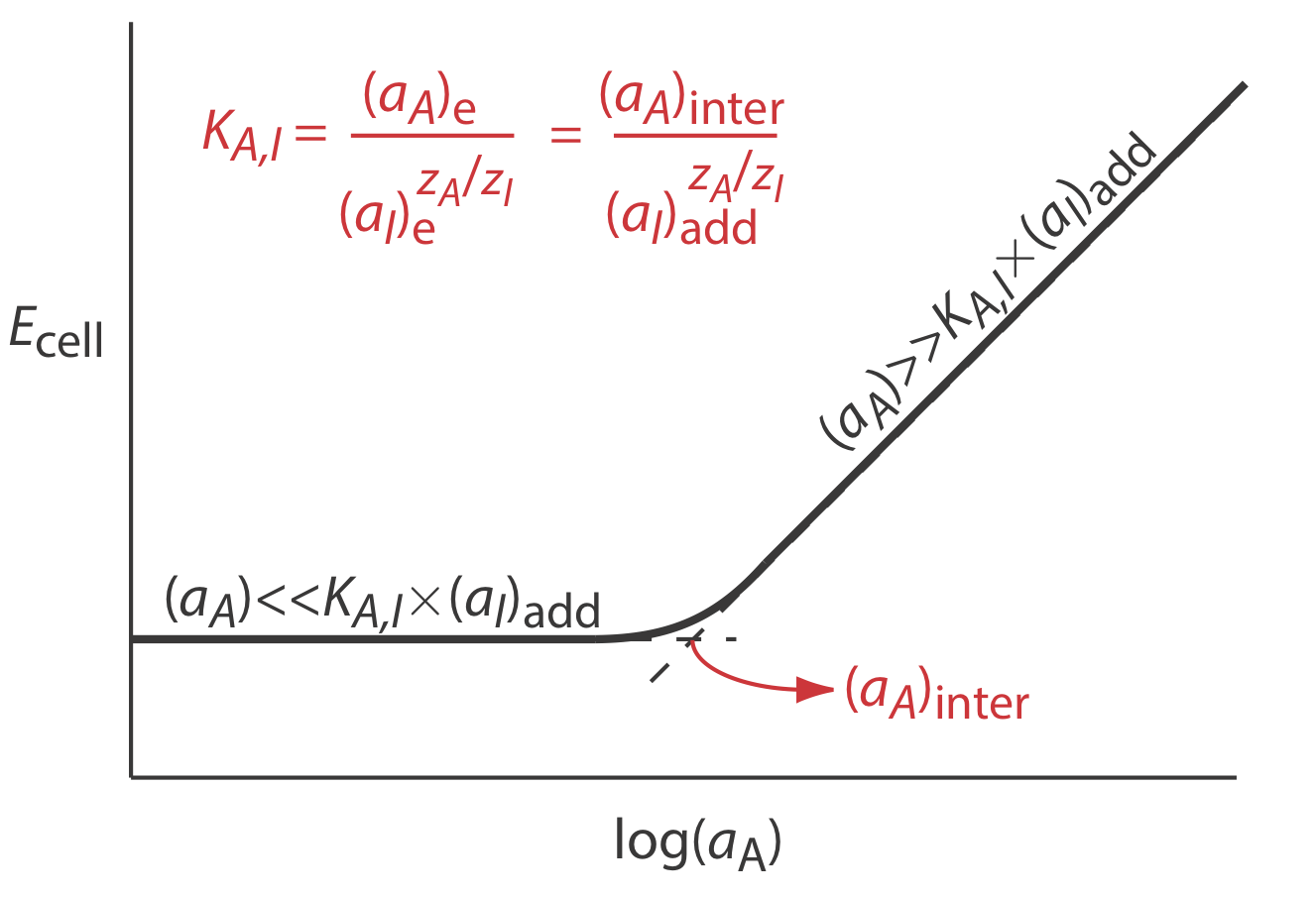
Los coeficientes de selectividad para la mayoría de los electrodos selectivos de iones disponibles comercialmente son proporcionados por el fabricante. Si no se conoce el coeficiente de selectividad, es fácil determinar su valor experimentalmente preparando una serie de soluciones, cada una de las cuales contiene la misma actividad de interferente, (a I) agregar, pero una actividad diferente de analito. Como se muestra en la Figura 11.2.9 , una gráfica del potencial celular frente al logaritmo de la actividad del analito tiene dos regiones lineales distintas. Cuando la actividad del analito es significativamente mayor que K A, I\(\times\) (a I) add, el potencial es una función lineal de log (a A), como lo da la Ecuación\ ref {11.7}. Si K A, I\(\times\) (a I) add es significativamente mayor que la actividad del analito, sin embargo, el potencial de la célula permanece constante. La actividad de analito e interferente en la intersección de estas dos regiones lineales se utiliza para calcular K A, I.
Sokalski y sus colaboradores describieron un método para preparar electrodos selectivos de iones con selectividades significativamente mejoradas [Sokalski, T.; Ceresa, A.; Zwicki, T.; Pretsch, E. J. Am. Chem. Soc. 1997, 119, 11347—11348]. Por ejemplo, un ISE convencional Pb 2 + tiene un valor\(\log K_{\text{Pb}^{2+}/\text{Mg}^{2+}}\) de —3.6. Si el potencial para una solución en la que la actividad de Pb 2 +\(4.1 \times 10^{-12}\) es idéntico al de una solución en la que la actividad de Mg 2 + es 0.01025, ¿cuál es el valor de\(\log K_{\text{Pb}^{2+}/\text{Mg}^{2+}}\) para su ISE?
Solución
Haciendo sustituciones apropiadas en la Ecuación\ ref {11.8}, encontramos que
\[K_{\text{Pb}^{2+}/\text{Mg}^{2+}} = \frac {(a_{\text{Pb}^{2+}})_e} {(a_{\text{Mg}^{2+}})_e^{z_{\text{Pb}^{2+}}/z_{\text{Mg}^{2+}}}} = \frac {4.1 \times 10^{-12}} {(0.01025)^{+2/+2}} = 4.0 \times 10^{-10} \nonumber\]
El valor de\(\log K_{\text{Pb}^{2+}/\text{Mg}^{2+}}\), por lo tanto, es —9.40.
Un electrodo selectivo de iones para\(\text{NO}_2^-\) tiene valores log K A , I de —3.1 para F —, —4.1 para\(\text{SO}_4^{2-}\), —1.2 para I — y —3.3 para\(\text{NO}_3^-\). ¿Qué ion es el interferente más grave y para qué actividad de este interferente es el potencial equivalente a una solución en la que\(\text{NO}_2^-\) se encuentra la actividad de\(2.75 \times 10^{-4}\)?
- Responder
-
Cuanto mayor sea el valor de K A, yo más grave es la interferencia. Valores mayores para K A, I corresponden a valores más positivos (menos negativos) para log K A , I; así, I —, con una K A, I de\(6.3 \times 10^{-2}\), es el más grave de estos interferentes. Para encontrar la actividad de I —que da un potencial equivalente a una\(\text{NO}_2^-\) actividad de\(2.75 \times 10^{-4}\), observamos que
\[a_{\text{NO}_2^-}=K_{A, I} \times a_{\text{I}^-} \nonumber\]
Hacer las sustituciones apropiadas
\[2.75 \times 10^{-4}=\left(6.3 \times 10^{-2}\right) \times a_{\mathrm{I}^-} \nonumber\]
y resolviendo para\(a_{\text{I}^-}\) da su actividad como\(4.4 \times 10^{-3}\).
Electrodos selectivos de iones de vidrio
Los primeros electrodos de vidrio comerciales se fabricaron utilizando Corning 015, un vidrio con una composición que es aproximadamente 22% Na 2 O, 6% CaO y 72% SiO 2. Cuando se sumerge en una solución acuosa durante varias horas, el exterior de aproximadamente 10 nm de la superficie de la membrana se hidrata, resultando en la formación de sitios cargados negativamente, —SiO —. Los iones sodio, Na +, sirven como contra-iones. Debido a que H + se une más fuertemente a —SiO — que Na +, desplazan los iones de sodio
\[\mathrm{H}^{+}+-\mathrm{SiO}^{-} \mathrm{Na}^{+}\rightleftharpoons-\mathrm{SiO}^{-} \mathrm{H}^{+}+\mathrm{Na}^{+} \nonumber\]
explicando la selectividad de la membrana para H +. El transporte de carga a través de la membrana es transportado por los iones Na +. El potencial de un electrodo de vidrio usando Corning 015 obedece a la ecuación
\[E_{\mathrm{cell}}=K+0.05916 \log a_{\mathrm{H}^{+}} \label{11.9}\]
en un rango de pH de aproximadamente 0.5 a 9. A valores de pH más básicos la membrana de vidrio responde más a otros cationes, como Na + y K +.
Para una membrana de vidrio Corning 015, el coeficiente de selectividad K H + /Na + es\(\approx 10^{-11}\). ¿Cuál es el error esperado si medimos el pH de una solución en la que se encuentra la actividad de H +\(2 \times 10^{-13}\) y la actividad de Na + es 0.05?
Solución
Una solución en la que la actividad real de H +, (a H +) actúa,\(2 \times 10^{-13}\) tiene un pH de 12.7. Debido a que el electrodo responde tanto a H + como a Na +, la actividad aparente de H +, (a H +) app, es
\[(a_{\text{H}^+})_\text{app} = (a_{\text{H}^+})_\text{act} + (K_{\text{H}^+ / \text{Na}^+} \times a_{\text{Na}^+}) = 2 \times 10^{-13} + (10^{-11} \times 0.05) = 7 \times 10^{-13} \nonumber\]
La actividad aparente de H + es equivalente a un pH de 12.2, un error de —0.5 unidades de pH.
La sustitución de Na 2 O y CaO por Li 2 O y BaO extiende el rango de pH útil de los electrodos de membrana de vidrio a niveles de pH mayores a 12.
Los electrodos de pH de membrana de vidrio a menudo están disponibles en una forma combinada que incluye tanto el electrodo indicador como el electrodo de referencia. El uso de un solo electrodo simplifica enormemente la medición del pH. Un ejemplo de un electrodo de combinación típico se muestra en la Figura 11.2.10 .
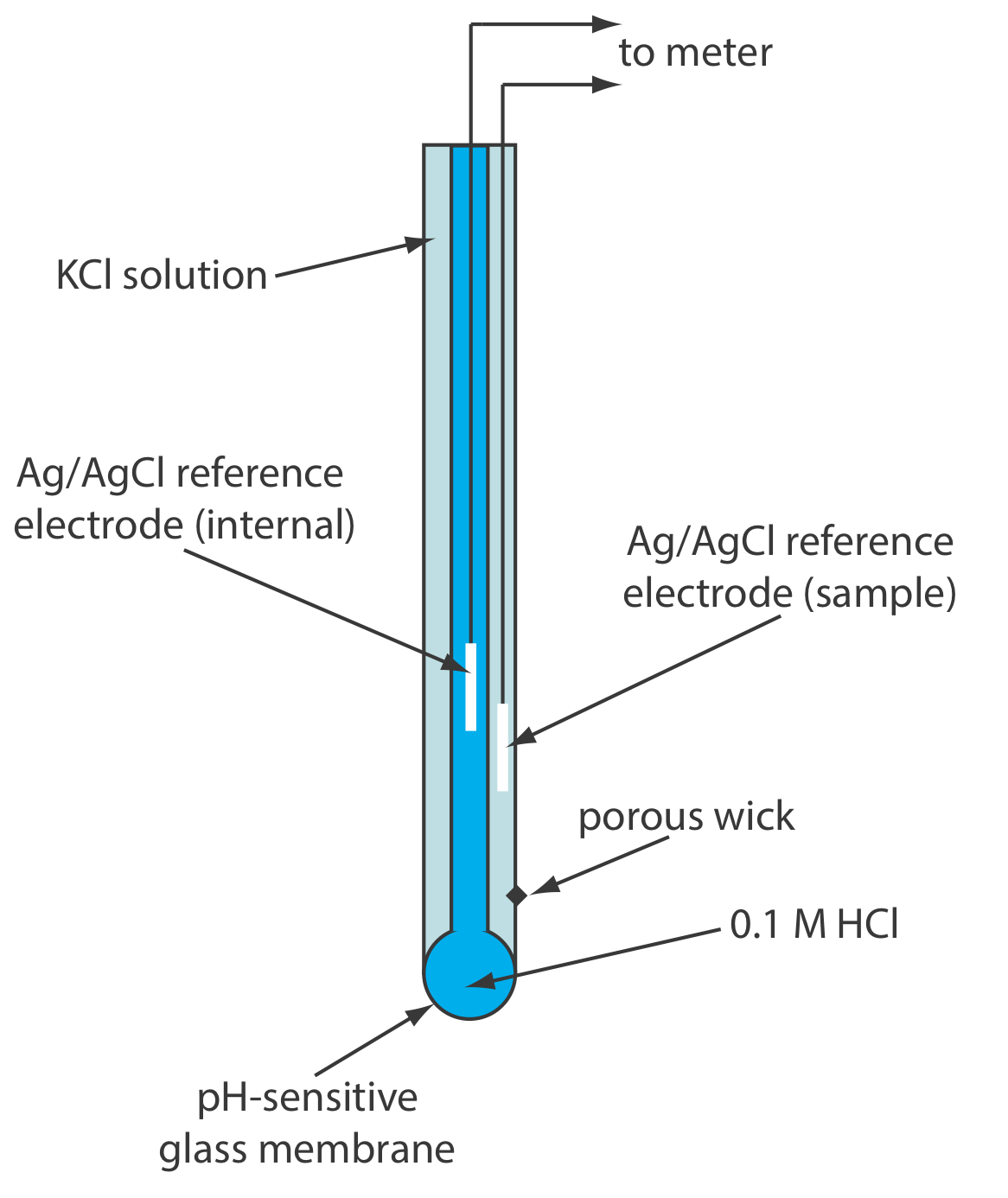
La observación de que la membrana de vidrio Corning 015 responde a iones distintos de H + (ver Ejemplo 11.2.6 ) condujo al desarrollo de membranas de vidrio con una mayor selectividad por otros cationes. Por ejemplo, se usa una membrana de vidrio con una composición de 11% de Na 2 O, 18% de Al 2 O 3 y 71% de SiO 2 como electrodo selectivo de iones para Na +. Se han desarrollado otros electrodos selectivos de iones de vidrio para el análisis de Li +, K +, Rb +, Cs +\(\text{NH}_4^+\), Ag + y Tl +. Table 11.2.1 proporciona varios ejemplos.
Debido a que la membrana de vidrio de un electrodo selectivo de iones es muy delgada (solo tiene aproximadamente 50 μm de grosor), deben manejarse con cuidado para evitar grietas o roturas. Los electrodos de vidrio generalmente se almacenan en un tampón de almacenamiento recomendado por el fabricante, lo que asegura que la superficie externa de la membrana permanezca hidratada. Si un electrodo de vidrio se seca, se reacondiciona remojándolo durante varias horas en una solución que contiene el analito. La composición de una membrana de vidrio cambiará con el tiempo, lo que afecta el rendimiento del electrodo. La vida útil promedio de un electrodo de vidrio típico es de varios años.
Electrodos selectivos de iones de estado sólido
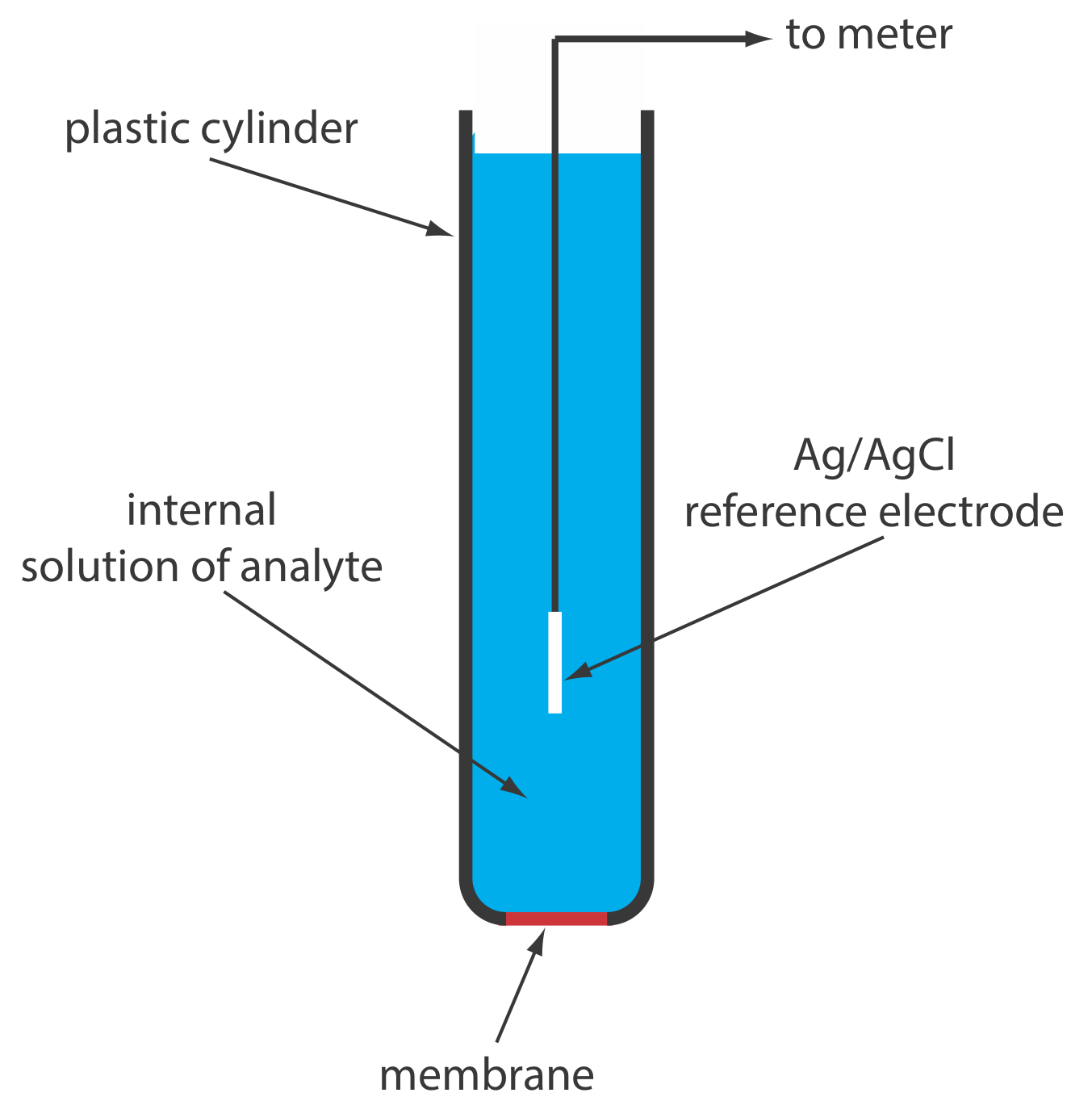
Un electrodo selectivo de iones en estado sólido tiene una membrana que consiste en una sal inorgánica policristalina o un solo cristal de una sal inorgánica. Podemos formar un electrodo policristalino selectivo de iones en estado sólido sellando un pellet de Ags de 1—2 mm de espesor, o una mezcla de AG y una segunda sal de plata u otro sulfuro metálico, en el extremo de un cilindro de plástico no conductor, llenando el cilindro con una solución interna que contenga el analito y colocando un electrodo de referencia en la solución interna. La figura 11.2.11 muestra un diseño típico.
El NaCl en un salero es un ejemplo de material policristalino porque consiste en muchos pequeños cristales de cloruro de sodio. Las placas de sal de NaCl utilizadas en la espectroscopia IR (ver Capítulo 10), por otro lado, son un ejemplo de un monocristal de cloruro de sodio.
El potencial de membrana para un pellet de Ag 2 S se desarrolla como resultado de una diferencia en la extensión de la reacción de solubilidad
\[\mathrm{Ag}_{2} \mathrm{S}(s)\rightleftharpoons2 \mathrm{Ag}^{+}(a q)+\mathrm{S}^{2-}(a q) \nonumber\]
en los dos lados de la membrana, con carga transportada a través de la membrana por iones Ag +. Cuando usamos el electrodo para monitorear la actividad de Ag +, el potencial celular es
\[E_{\text {cell }}=K+0.05916 \log a_{\mathrm{Ag}^{+}} \nonumber\]
La membrana también responde a la actividad de\(\text{S}^{2-}\), con un potencial celular de
\[E_{\mathrm{cell}}=K-\frac{0.05916}{2} \log a_{\text{S}^{2-}} \nonumber\]
Si combinamos una sal de plata insoluble, como AgCl, con el Ag 2 S, entonces el potencial de membrana también responde a la concentración de Cl —, con un potencial celular de
\[E_{\text {cell }}=K-0.05916 \log a_{\mathrm{Cl}^{-}} \nonumber\]
Al mezclar Ag 2 S con CdS, Cu o PbS, podemos hacer un electrodo selectivo de iones que responda a la actividad de Cd 2 +, Cu 2+ o Pb 2 +. En este caso el potencial celular es
\[E_{\mathrm{cell}}=K+\frac{0.05916}{2} \ln a_{M^{2+}} \nonumber\]
donde un M 2 + es la actividad del ión metálico.
La Tabla 11.2.2 proporciona ejemplos de electrodos selectivos de iones de estado sólido basados en Ag 2 policristalinos. La selectividad de estos electrodos selectivos de iones depende de la solubilidad relativa de los compuestos. Un Cl — ISE usando una membrana Ag 2 S/AgCl es más selectivo para Br — (K Cl — /Br — = 10 2) y para I — (K Cl — /I — = 10 6) porque AgBr y AgI son menos solubles que AgCl. Si la actividad de Br — es suficientemente alta, AgCl en la interfaz membrana/solución es reemplazado por AgBr y la respuesta del electrodo a Cl — disminuye sustancialmente. La mayoría de los electrodos policristalinos selectivos de iones enumerados en la Tabla 11.2.2 operan en un rango extendido de niveles de pH. El equilibrio entre S 2— y HS — limita el análisis para S2— a un rango de pH de 13—14.
La membrana de un electrodo selectivo de iones F se forma a partir de un solo cristal de LaF 3, que generalmente está dopado con una pequeña cantidad de EuF 2 para mejorar la conductividad de la membrana. Debido a que EuF 2 proporciona solo dos iones F, en comparación con los tres iones F, en LaF 3, cada EuF 2 produce una vacante en la red cristalina. Los iones fluoruro pasan a través de la membrana moviéndose a las vacantes adyacentes. Como se muestra en la Figura 11.2.11 , la membrana LaF 3 se sella en el extremo de un cilindro de plástico no conductor, que contiene una solución estándar de F —, típicamente 0.1 M NaF, y un electrodo de referencia Ag/AgCl.
El potencial de membrana para un F — ISE resulta de una diferencia en la solubilidad de LaF 3 en lados opuestos de la membrana, con el potencial dado por
\[E_{\mathrm{cell}}=K-0.05916 \log a_{\mathrm{F}^-} \nonumber\]
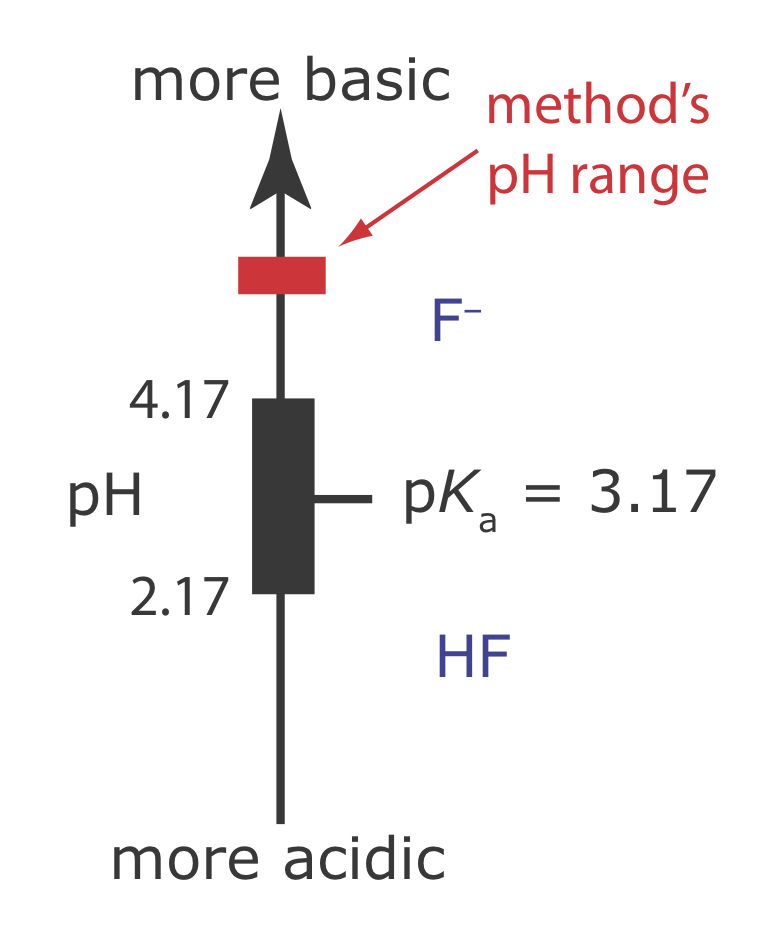
Una ventaja del electrodo selectivo de iones F es su libertad de interferencia. La única excepción significativa es OH — (K F — /OH — = 0.1), que impone un límite máximo de pH para un análisis exitoso. Por debajo de un pH de 4 la forma predominante de fluoruro en solución es HF, que no contribuye al potencial de membrana. Por esta razón, se realiza un análisis de fluoruro a un pH mayor a 4.
¿Cuál es el pH máximo que podemos tolerar si necesitamos analizar una solución en la que la actividad de F — sea\(1 \times 10^{-5}\) con un error inferior al 1%?
Solución
En presencia de OH — el potencial celular es
\[E_{\mathrm{cell}}=K-0.05916\left\{a_{\mathrm{F}^-}+K_{\mathrm{F}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^-}\right\} \nonumber\]
Para lograr un error inferior al 1%, el término\(K_{\mathrm{F}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^-}\) debe ser inferior al 1% de un F —; así
\[K_{\mathrm{F}^- / \mathrm{OH}^-} \times a_{\mathrm{OH}^{-}} \leq 0.01 \times a_{\mathrm{F}^-} \nonumber\]
\[0.10 \times a_{\mathrm{OH}^{-}} \leq 0.01 \times\left(1.0 \times 10^{-5}\right) \nonumber\]
Resolviendo para un OH — da la actividad máxima permisible para OH — as\(1 \times 10^{-6}\), que corresponde a un pH de menos de 8.
Supongamos que desea utilizar el electrodo selectivo de nitritos en Ejercicio 11.2.5 para medir la actividad de\(\text{NO}_2^-\). Si la actividad de\(\text{NO}_2^-\) es\(2.2 \times 10^{-4}\), ¿cuál es el pH máximo que puede tolerar si el error debido al OH — debe ser inferior al 10%? El coeficiente de selectividad para OH —,\(K_{\text{NO}_2^-/\text{OH}^-}\), es 630. ¿Esperas que el electrodo tenga un límite de pH más bajo? Explica claramente tu respuesta.
- Responder
-
En presencia de OH — el potencial celular es
\[E_{\mathrm{cell}}=K-0.05916 \log \left\{a_{\mathrm{NO}_{2}^-}+K_{\mathrm{NO}_{2}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^{-}}\right\} \nonumber\]
Para lograr un error inferior al 10%, el término\(K_{\mathrm{NO}_{2}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^{-}}\) debe ser inferior al 1% de\(a_{\text{NO}_2^-}\); así
\[K_{\mathrm{NO}_{2}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^-} \leq 0.10 \times a_{\mathrm{NO}_{2}^-} \nonumber\]
\[630 \times a_{\mathrm{OH}^{-}} \leq 0.10 \times\left(2.2 \times 10^{-4}\right) \nonumber\]
Resolviendo para un OH — da su máxima actividad permisible como\(3.5 \times 10^{-8}\), que corresponde a un pH inferior a 6.54.
El electrodo sí tiene un límite de pH inferior. El nitrito es la base débil conjugada de HNO 2, una especie a la que el ISE no responde. Como se muestra en el diagrama de escalera a continuación, a un pH de 4.15 aproximadamente 10% de nitrito está presente como HNO 2. Un pH mínimo de 4.5 es la recomendación habitual cuando se usa un ISE de nitrito. Esto corresponde a una\(\text{NO}_2^- / \text{HNO}_2\) proporción de
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\mathrm{NO}_{2}^{-}\right]}{\left[\mathrm{HNO}_{2}\right]} \nonumber\]
\[4.5=3.15+\log \frac{\left[\mathrm{NO}_{2}^{-}\right]}{\left[\mathrm{HNO}_{2}\right]} \nonumber\]
\[\frac{\left[\mathrm{NO}_{2}^{-}\right]}{\left[\mathrm{HNO}_{2}\right]} \approx 22 \nonumber\]
Así, a un pH de 4.5 aproximadamente 96% de nitrito está presente como\(\text{NO}_2^-\).
A diferencia de un electrodo selectivo de iones de membrana de vidrio, un ISE de estado sólido no necesita ser acondicionado antes de ser utilizado, y puede almacenarse en seco. La superficie del electrodo está sujeta a envenenamiento, como se describió anteriormente para un Cl — ISE en contacto con una concentración excesiva de Br —. Si un electrodo es envenenado, puede ser devuelto a su estado original lijando y puliendo la membrana cristalina.
Envenenamiento simplemente significa que la superficie ha sido modificada químicamente, como AgBr que se forma en la superficie de una membrana de AgCl.
Electrodos selectivos de iones basados en líquidos
Otra clase de electrodos selectivos de iones utiliza una membrana hidrófoba que contiene un agente complejante orgánico líquido que reacciona selectivamente con el analito. Se han utilizado tres tipos de agentes complejantes orgánicos: intercambiadores catiónicos, intercambiadores aniónicos e ionóforos neutros. Existe un potencial de membrana si la actividad del analito es diferente en los dos lados de la membrana. La corriente es transportada a través de la membrana por el analito.
Un ionóforo es un ligando cuyo exterior es hidrófobo y cuyo interior es hidrófilo. El éter corona que se muestra aquí es un ejemplo de un ionóforo neutro.
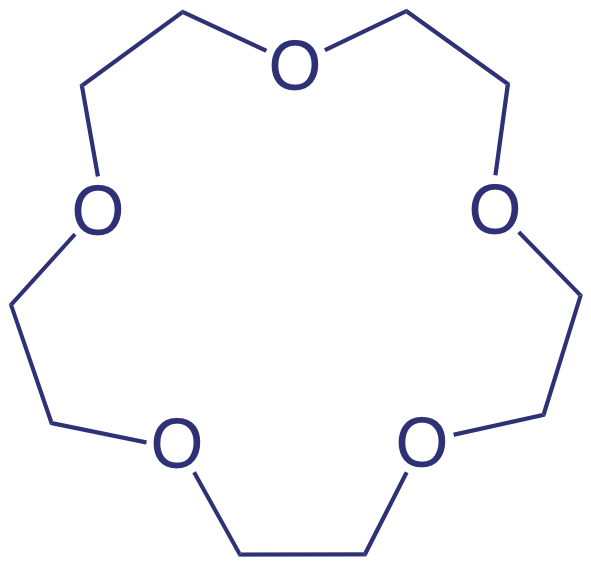
Un ejemplo de un electrodo selectivo de iones basado en líquido es el de Ca 2 +, que utiliza una membrana plástica porosa saturada con el intercambiador catiónico di- (n-decil) fosfato. Como se muestra en la Figura 11.2.12 , la membrana se coloca en el extremo de un tubo cilíndrico no conductor y está en contacto con dos depósitos. El reservorio externo contiene di- (n-decil) fosfato en di-n-octilfenilfosfonato, el cual se empapa en la membrana porosa. El depósito interno contiene una solución acuosa estándar de Ca 2 + y un electrodo de referencia de Ag/AgCl. También están disponibles electrodos selectivos de iones de calcio en los que el fosfato de di- (n-decilo) se inmoviliza en una membrana de cloruro de polivinilo (PVC) que elimina la necesidad del reservorio externo.
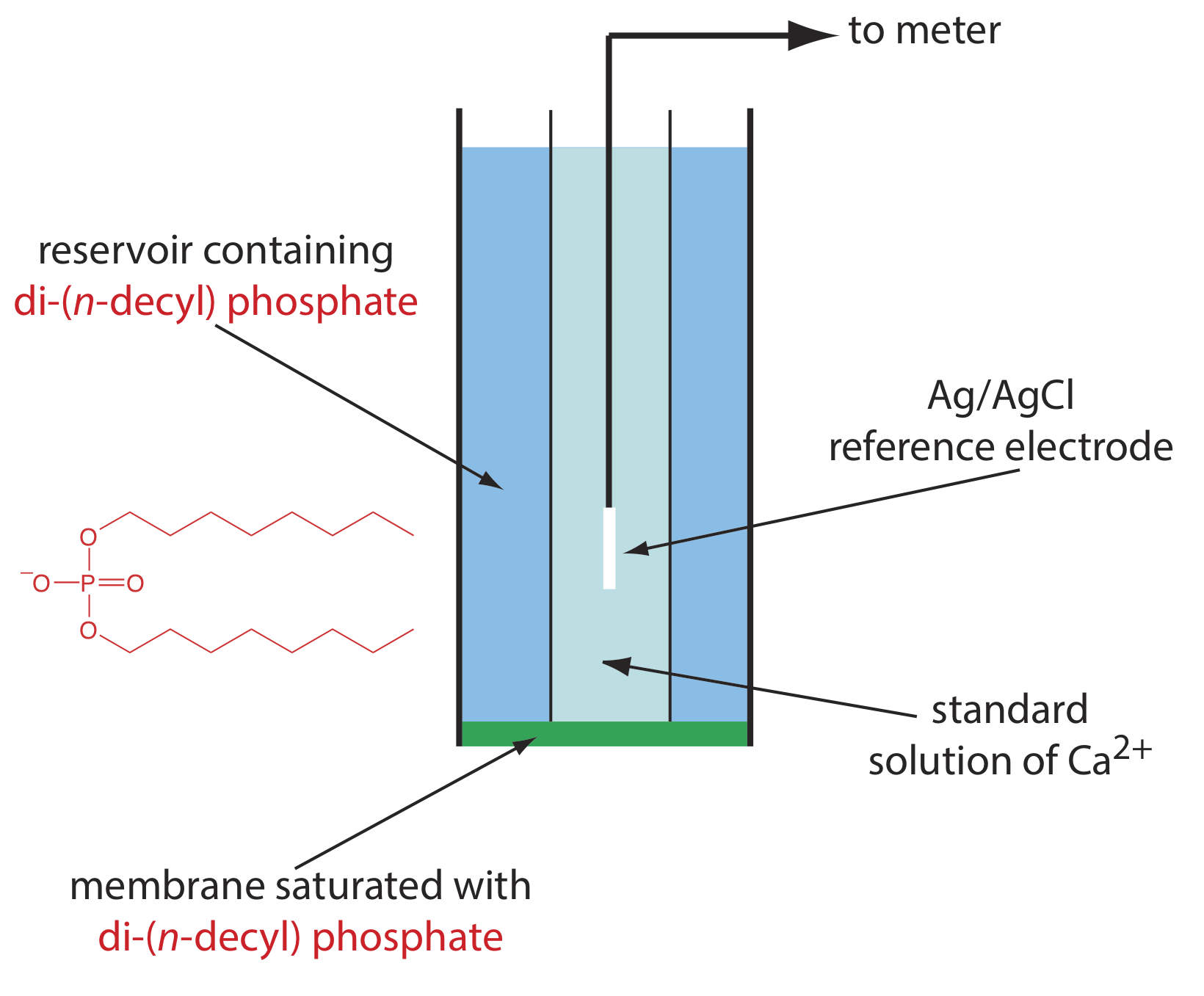
El potencial de membrana para el ISE Ca 2 + se desarrolla como resultado de una diferencia en la extensión de la reacción de complejación
\[\mathrm{Ca}^{2+}(a q)+2\left(\mathrm{C}_{10} \mathrm{H}_{21} \mathrm{O}\right)_{2} \mathrm{PO}_{2}^{-}(mem) \rightleftharpoons \mathrm{Ca}\left[\left(\mathrm{C}_{10} \mathrm{H}_{21} \mathrm{O}\right)_{2} \mathrm{PO}_{2}\right]_2 (mem) \nonumber\]
en los dos lados de la membrana, donde (mem) indica una especie que está presente en la membrana. El potencial celular para el electrodo selectivo de iones Ca 2 + es
\[E_{\mathrm{cell}}=K+\frac{0.05916}{2} \log a_{\mathrm{ca}^{2+}} \nonumber\]
La selectividad de este electrodo para Ca 2 + es muy buena, con solo Zn 2 + mostrando mayor selectividad.
En la Tabla 11.2.3 se enumeran las propiedades de varios electrodos selectivos de iones basados en líquidos. Un electrodo que utiliza un depósito de líquido se puede almacenar en una solución diluida de analito y no necesita acondicionamiento adicional antes de su uso. La vida útil de un electrodo con membrana de PVC, sin embargo, es proporcional a su exposición a soluciones acuosas. Por esta razón estos electrodos se almacenan mejor cubriendo la membrana con una tapa junto con una pequeña cantidad de gasa humedecida para mantener un ambiente húmedo. Antes de usar el electrodo se acondiciona en una solución de analito durante 30—60 minutos.
Electrodos de detección de gas
Varios electrodos de membrana responden a la concentración de un gas disuelto. El diseño básico de un electrodo sensor de gas, como se muestra en la Figura 11.2.13 , consiste en una membrana delgada que separa la muestra de una solución interna que contiene un electrodo selectivo de iones. La membrana es permeable al analito gaseoso, pero impermeable a los componentes no volátiles en la matriz de la muestra. El analito gaseoso pasa a través de la membrana donde reacciona con la solución interna, produciendo una especie cuya concentración es monitoreada por el electrodo selectivo de iones. Por ejemplo, en un electrodo de CO 2, el CO 2 se difunde a través de la membrana donde reacciona en la solución interna para producir H 3 O +.
El cambio en la actividad de H 3 O + en la solución interna se monitorea con un electrodo de pH, para lo cual el potencial celular viene dado por la Ecuación\ ref {11.9}. Para encontrar la relación entre la actividad de H 3 O + en la solución interna y la actividad del CO 2 en la solución interna reorganizamos la expresión constante de equilibrio para la reacción\ ref {11.10}; así
donde K a es la constante de equilibrio. Si la actividad de\(\text{HCO}_3^-\) en la solución interna es suficientemente grande, entonces su actividad no se ve afectada por la pequeña cantidad de CO 2 que pasa a través de la membrana. Sustituyendo la ecuación\ ref {11.11} en la ecuación\ ref {11.9} da
\[E_{\mathrm{cell}}=K^{\prime}+0.05916 \log a_{\mathrm{co}_{2}} \nonumber\]
donde K′ es una constante que incluye la constante para el electrodo de pH, la constante de equilibrio para la reacción\ ref {11.10} y la actividad de\(\text{HCO}_3^-\) en la solución interna.
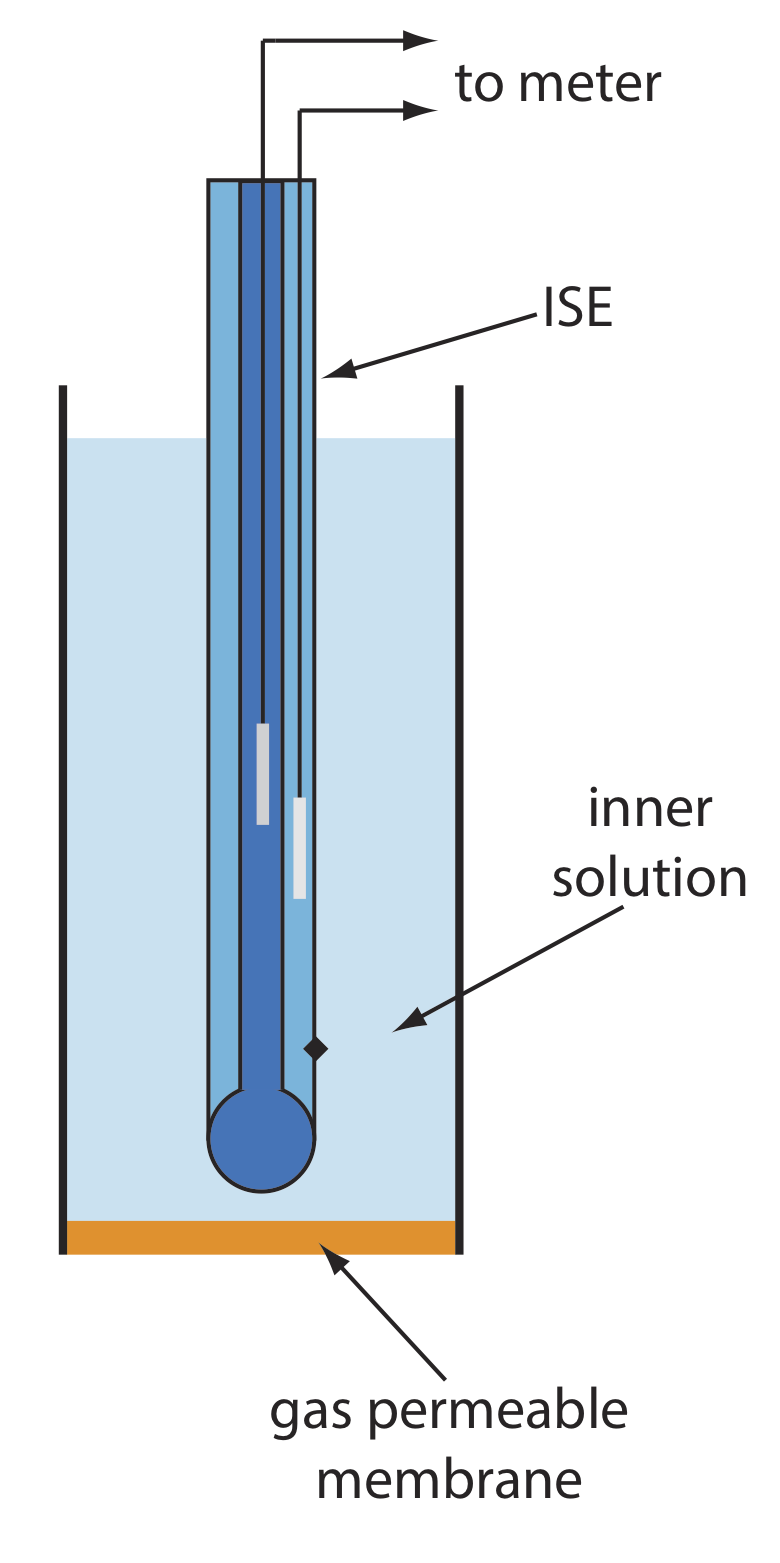
En la Tabla 11.2.4 se enumeran las propiedades de varios electrodos sensores de gas. La composición de la solución interna cambia con el uso, y tanto la solución interna como la membrana deben reemplazarse periódicamente. Los electrodos sensores de gas se almacenan en una solución similar a la solución interna para minimizar su exposición a los gases atmosféricos.
Biosensores Potenciométricos
El enfoque para el desarrollo de electrodos sensores de gas se puede modificar para crear electrodos potenciométricos que respondan a especies bioquímicamente importantes. La clase más común de biosensores potenciométricos son los electrodos enzimáticos, en los que atrapamos o inmovilizamos una enzima en la superficie de un electrodo potenciométrico. La reacción del analito con la enzima produce un producto cuya concentración es monitoreada por el electrodo potenciométrico. Los biosensores potenciométricos también se han diseñado alrededor de otras especies biológicamente activas, incluyendo anticuerpos, partículas bacterianas, tejidos y receptores hormonales.
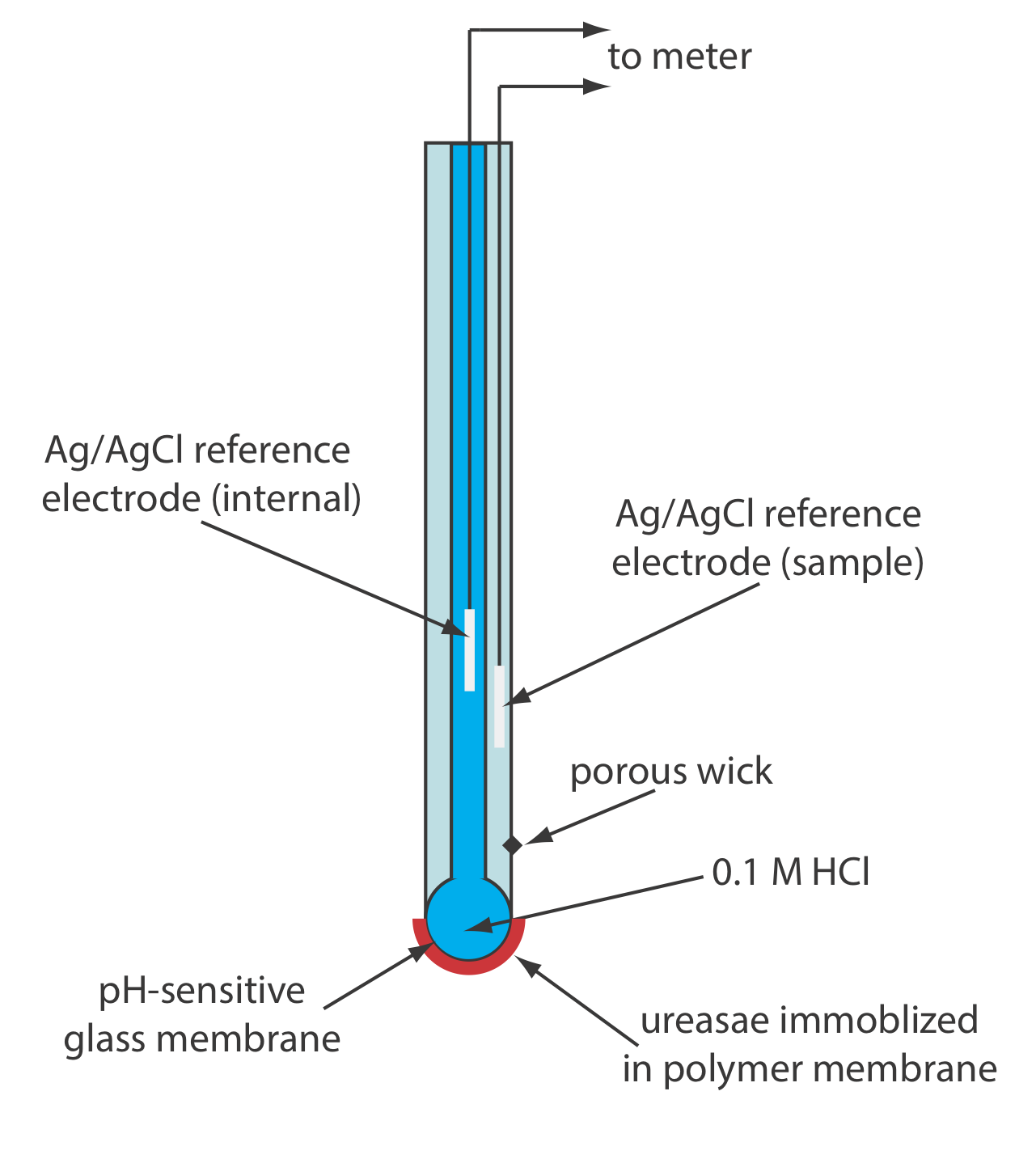
Un ejemplo de un electrodo enzimático es el electrodo de urea, que se basa en la hidrólisis catalítica de la urea por la ureasa
\[\mathrm{CO}\left(\mathrm{NH}_{2}\right)_{2}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons 2 \mathrm{NH}_{4}^{+}(a q)+\text{ CO}_{3}^{-}(a q) \nonumber\]
La Figura 11.2.14 muestra una versión del electrodo de urea, que modifica un electrodo NH 3 con detección de gas añadiendo una membrana de diálisis que atrapa una solución tamponada de ureasa a pH 7.0 entre la membrana de diálisis y la membrana permeable a los gases [(a) Papastathopoulos, D. S.; Rechnitz, G. A. Anal. Chim. Acta 1975, 79, 17—26; b) Riechel, T. L. J. Chem. Educ. 1984, 61, 640—642]. Un electrodo NH 3, como se muestra en la Tabla 11.2.4 , utiliza una membrana permeable a los gases y un electrodo de pH de vidrio. El NH 3 se difunde a través de la membrana donde cambia el pH de la solución interna.
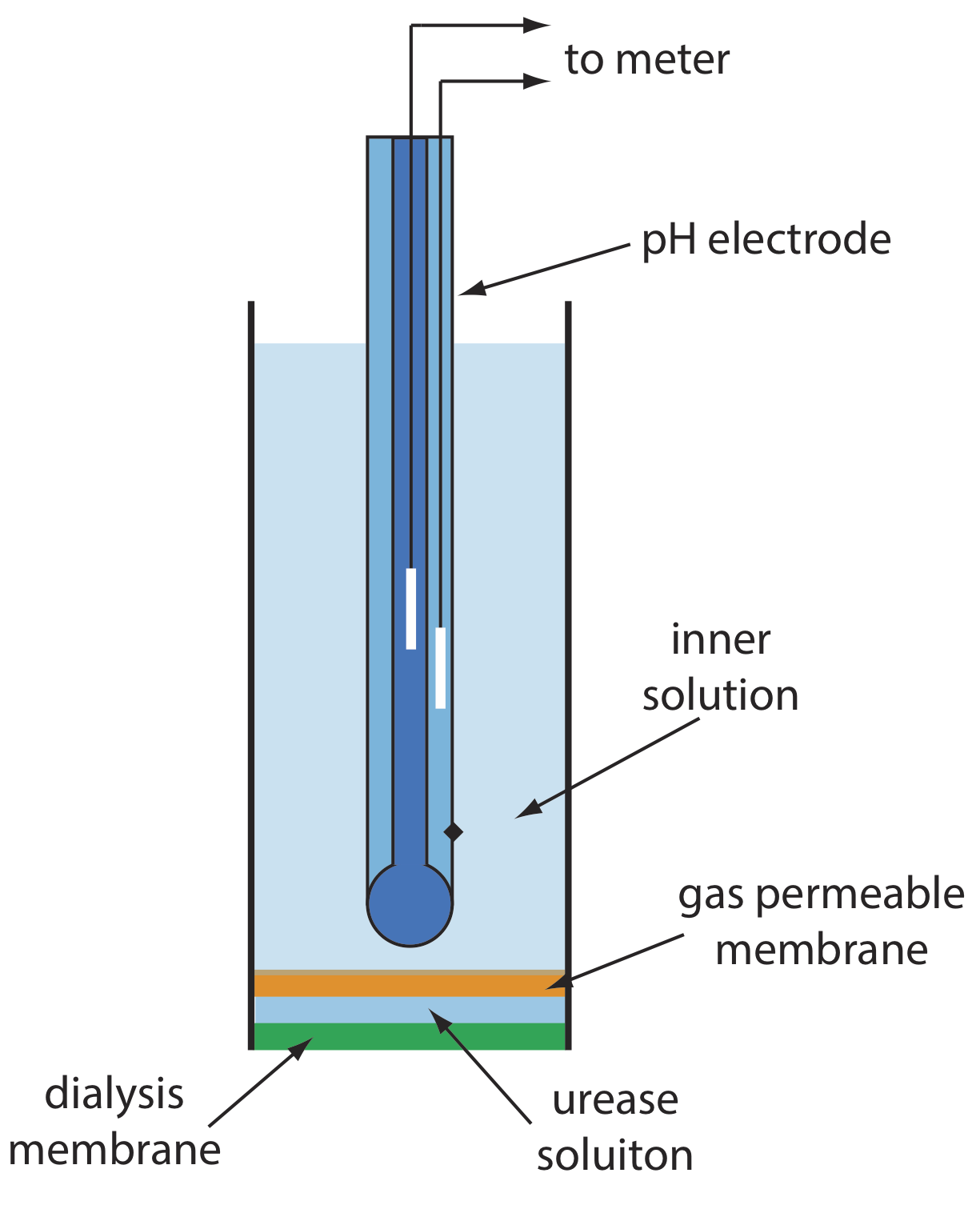
Al sumergirse en la muestra, la urea se difunde a través de la membrana de diálisis donde reacciona con la enzima ureasa para formar el ión amonio\(\text{NH}_4^+\), que se encuentra en equilibrio con NH 3.
\[\mathrm{NH}_{4}^{+}(a q)+\mathrm{H}_{2} \mathrm{O}(l ) \rightleftharpoons \text{ H}_{3} \mathrm{O}^{+}(a q)+\text{ NH}_{3}(a q) \nonumber\]
El NH 3, a su vez, se difunde a través de la membrana permeable a los gases donde un electrodo de pH mide el cambio resultante en el pH. La respuesta del electrodo a la concentración de urea es
\[E_{\text {cell }}=K-0.05916 \log a_{\text {urea }} \label{11.12}\]
Otra versión del electrodo de urea (Figura 11.2.15 ) inmoviliza la enzima ureasa en una membrana polimérica formada directamente en la punta de un electrodo de pH de vidrio [Tor, R.; Freeman, A. Anal. Chem. 1986, 58, 1042—1046]. En este caso la respuesta del electrodo es
\[\mathrm{pH}=K a_{\mathrm{urea}} \label{11.13}\]
Pocos biosensores potenciométricos están disponibles comercialmente. Como se muestra en la Figura 11.2.14 y la Figura 11.2.15 , sin embargo, es posible convertir un electrodo selectivo de iones o un electrodo sensor de gas en un biosensor. En la Tabla 11.2.5 se describen varios ejemplos representativos y se pueden encontrar ejemplos adicionales en los recursos adicionales de este capítulo.
Aplicaciones Cuantitativas
La determinación potenciométrica de la concentración de un analito es una de las técnicas analíticas cuantitativas más comunes. Quizás la medición analítica más frecuente es la determinación del pH de una solución, una medida que consideraremos con más detalle más adelante en esta sección. Otras áreas donde la potenciometría es importante son la química clínica, la química ambiental y las titulaciones potenciométricas. Antes de considerar aplicaciones representativas, sin embargo, necesitamos examinar más de cerca la relación entre el potencial celular y la concentración del analito y los métodos para estandarizar las mediciones potenciométricas.
Actividad y Concentración
La ecuación de Nernst relaciona el potencial celular con la actividad del analito. Por ejemplo, la ecuación de Nernst para un electrodo metálico de primer tipo es
\[E_{\mathrm{cll}}=K+\frac{0.05916}{n} \log a_{M^{n+}} \label{11.14}\]
donde un M n + es la actividad del ion metálico. Sin embargo, cuando usamos un electrodo potenciométrico, nuestro objetivo es determinar la concentración del analito. Como aprendimos en el Capítulo 6, la actividad de un ión es producto de su concentración, [M n +], y un coeficiente de actividad dependiente de la matriz,\(\gamma_{Mn^{n+}}\).
\[a_{M^{n+}}=\left[M^{n+}\right] \gamma_{M^{n+}} \label{11.15}\]
Sustituyendo la ecuación\ ref {11.15} en la ecuación\ ref {11.14} y reordenando, da
Podemos resolver la Ecuación\ ref {11.16} para la concentración del ión metálico si conocemos el valor para su coeficiente de actividad. Desafortunadamente, si no conocemos la composición iónica exacta de la matriz de la muestra, que es la situación habitual, entonces no podemos calcular el valor de\(\gamma_{Mn^{n+}}\). Hay una solución a este dilema. Si diseñamos nuestro sistema para que los estándares y las muestras tengan una matriz idéntica, entonces el valor de\(\gamma_{Mn^{n+}}\) permanece constante y la Ecuación\ ref {11.16} simplifica a
\[E_{\mathrm{cell}}=K^{\prime}+\frac{0.05916}{n} \log \left[M^{n+}\right] \nonumber\]
donde\(K^{\prime}\) incluye el coeficiente de actividad.
Análisis cuantitativo mediante estándares externos
Antes de poder determinar la concentración de analito en una muestra, debemos estandarizar el electrodo. Si la respuesta del electrodo obedece a la ecuación de Nernst, entonces podemos determinar la constante K usando un único estándar externo. Debido a que una pequeña desviación de la pendiente ideal de ± RT/nF o ± RT/zF no es inesperada, generalmente usamos dos o más estándares externos.
Para revisar el uso de estándares externos, consulte el Capítulo 5.3.
En ausencia de interferentes, una curva de calibración de célula E versus log a A, donde A es el analito, es una línea recta. Una gráfica de célula E versus log [A], sin embargo, puede mostrar curvatura a mayores concentraciones de analito como resultado de un cambio dependiente de la matriz en el coeficiente de actividad del analito. Para mantener una matriz consistente agregamos una alta concentración de un electrolito inerte a todas las muestras y estándares. Si la concentración de electrolito agregado es suficiente, entonces la diferencia entre la matriz de la muestra y la matriz de los estándares no afectará la fuerza iónica y el coeficiente de actividad esencialmente permanece constante. El electrolito inerte agregado a la muestra y los estándares se denomina tampón de ajuste de fuerza iónica total (TISAB).
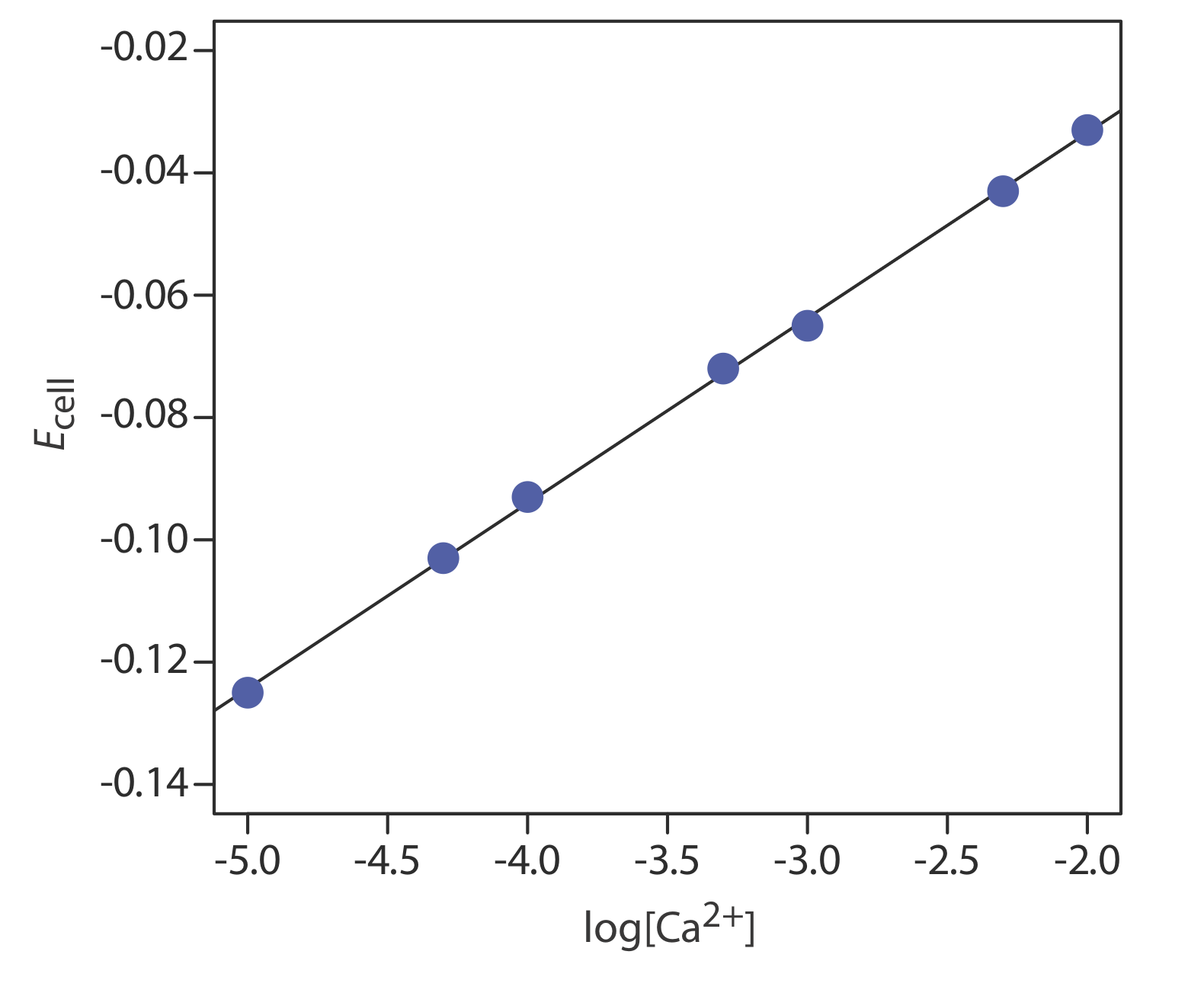
La concentración de Ca 2 + en una muestra de agua se determina mediante el método de estándares externos. La fuerza iónica de las muestras y los estándares se mantiene a un nivel casi constante haciendo que cada solución sea 0.5 M en KNO 3. Los potenciales celulares medidos para los estándares externos se muestran en la siguiente tabla.
| [Ca 2+] (M) | Celda E (V) |
|---|---|
|
\(1.00 \times 10^{-5}\) |
—0.125 |
| \(5.00 \times 10^{-5}\) | —0.103 |
| \(1.00 \times 10^{-4}\) | —0.093 |
| \(5.00 \times 10^{-4}\) | —0.072 |
| \(1.00 \times 10^{-3}\) | —0.063 |
| \(5.00 \times 10^{-3}\) | —0.043 |
| \(1.00 \times 10^{-2}\) | —0.033 |
¿Cuál es la concentración de Ca 2 + en una muestra de agua si se encuentra que su potencial celular es —0.084 V?
Solución
La regresión lineal da la curva de calibración en la Figura 11.2.16 , con una ecuación de
\[E_{\mathrm{cell}}=0.027+0.0303 \log \left[\mathrm{Ca}^{2+}\right] \nonumber\]
Sustituir el potencial celular de la muestra da la concentración de Ca 2 + como\(2.17 \times 10^{-4}\) M. Obsérvese que la pendiente de la curva de calibración, que es 0.0303, es ligeramente mayor que su valor ideal de 0.05916/2 = 0.02958; esto no es inusual y es una razón para usar múltiples estándares.
Una razón por la que no es inusual encontrar que la pendiente experimental se desvía de su valor ideal de 0.05916/ n es que este valor ideal supone que la temperatura es de 25°C.
Análisis cuantitativo mediante el método de adiciones estándar
Otro enfoque para calibrar un electrodo potenciométrico es el método de adiciones estándar. Primero, transferimos una muestra con un volumen de V samp y una concentración de analito de C samp a un vaso de precipitados y medimos el potencial, (célula E) samp. A continuación, hacemos una adición estándar agregando a la muestra un pequeño volumen, V std, de un estándar que contiene una concentración conocida de analito, C std, y medimos el potencial, (celda E) std. Si V std es significativamente menor que V samp, entonces podemos ignorar con seguridad el cambio en la matriz de la muestra y asumir que el coeficiente de actividad del analito es constante. El ejemplo 11.2.9 demuestra cómo podemos usar una adición estándar de un punto para determinar la concentración de analito en una muestra.
Para revisar el método de adiciones estándar, consulte el Capítulo 5.3.
La concentración de Ca 2+ en una muestra de agua de mar se determina usando un electrodo selectivo de iones Ca y una adición estándar de un punto. Una muestra de 10.00 ml se transfiere a un matraz aforado de 100 ml y se diluye a volumen. Se coloca una alícuota de 50.00-mL de la muestra en un vaso de precipitados con el ISE de Ca y un electrodo de referencia, y el potencial se mide como —0.05290 V. Después de agregar una alícuota de 1.00-mL de una solución estándar\(5.00 \times 10^{-2}\) M de Ca 2 + el potencial es —0.04417 V. Cuál es la concentración de Ca 2 + en la muestra de agua de mar?
Solución
Para comenzar, escribimos la ecuación de Nernst antes y después de agregar la suma estándar. El potencial celular para la muestra es
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{samp}}=K+\frac{0.05916}{2} \log C_{\mathrm{samp}} \nonumber\]
y que siguiendo la adición estándar es
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{std}}=K+\frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} \nonumber\]
donde V tot es el volumen total (V samp + V std) después de la adición estándar. Restar la primera ecuación de la segunda ecuación da
\[\Delta E = \left(E_{\mathrm{cell}}\right)_{\mathrm{std}} - \left(E_{\mathrm{cell}}\right)_{\mathrm{samp}} = \frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} - \frac{0.05916}{2}\log C_\text{samp} \nonumber\]
Reorganizar esta ecuación nos deja con
\[\frac{2 \Delta E_{cell}}{0.05916} = \log \left\{ \frac {V_\text{samp}} {V_\text{tot}} + \frac {V_\text{std}C_\text{std}} {V_\text{tot}C_\text{samp}} \right\} \nonumber\]
Sustituyendo valores conocidos por\(\Delta E\), V samp, V std, V tot y C std,
\[\begin{array}{l}{\frac{2 \times\{-0.04417-(-0.05290)\}}{0.05916}=} \\ {\log \left\{\frac{50.00 \text{ mL}}{51.00 \text{ mL}}+\frac{(1.00 \text{ mL})\left(5.00 \times 10^{-2} \mathrm{M}\right)}{(51.00 \text{ mL}) C_{\mathrm{samp}}}\right\}} \\ {0.2951=\log \left\{0.9804+\frac{9.804 \times 10^{-4}}{C_{\mathrm{samp}}}\right\}}\end{array} \nonumber\]
y tomando el log inverso de ambos lados da
\[1.973=0.9804+\frac{9.804 \times 10^{-4}}{C_{\text {samp }}} \nonumber\]
Finalmente, resolviendo para C samp da la concentración de Ca 2 + como\(9.88 \times 10^{-4}\) M. Debido a que diluimos la muestra original de agua de mar por un factor de 10, la concentración de Ca 2 + en la muestra de agua de mar es\(9.88 \times 10^{-3}\) M.
Iones libres versus iones complejados
La mayoría de los electrodos potenciométricos son selectivos hacia la forma libre y no complejada del analito, y no responden a ninguna de las formas complejadas del analito. Esta selectividad proporciona a los electrodos potenciométricos una ventaja significativa sobre otros métodos cuantitativos de análisis si es necesario determinar la concentración de iones libres. Por ejemplo, el calcio está presente en la orina tanto como iones Ca 2+ libres como iones Ca 2+ unidos a proteínas. Si analizamos una muestra de orina mediante espectroscopia de absorción atómica, la señal es proporcional a la concentración total de Ca 2+ porque tanto el calcio libre como el unido están atomizados. El análisis de orina con un ISE de Ca 2+, sin embargo, da una señal que es función de solo iones libres de Ca 2+ porque el Ca 2+ unido a proteína no puede interactuar con la membrana del electrodo.
La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método analítico típico. Si bien cada método es único, la siguiente descripción de la determinación de F — en pasta de dientes proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en Kennedy, J. H. Analytical Chemistry— Practice, Harcourt Brace Jaovanovich: San Diego, 1984, p. 117—118.
Método Representativo 11.2.1: Determinación de Fluoruro en Pasta Dental
Descripción del Método
La concentración de fluoruro en pastas dentales que contienen F soluble — se determina con un electrodo F — selectivo de iones usando una curva de calibración preparada con estándares externos. Aunque el F — ISE es muy selectivo (solo OH — con un K F — /OH — de 0.1 es un interferente significativo), Fe 3 + y Al 3 + interfieren con el análisis porque forman solubles complejos de fluoruro que no interactúan con la membrana del electrodo selectivo de iones. Esta interferencia se minimiza haciendo reaccionar cualquier Fe 3 + y Al 3 + con un agente complejante adecuado.
Procedimiento
Prepare 1 L de una solución estándar de 1.00% p/v SnF 2 y transfiérala a una botella de plástico para su almacenamiento. Usando esta solución, se preparan 100 mL cada uno de los patrones que contienen 0.32%, 0.36%, 0.40%, 0.44% y 0.48% p/v SnF 2, agregando 400 mg de ácido málico a cada solución como estabilizador. Transfiera los estándares a botellas de plástico para su almacenamiento. Preparar un tampón de ajuste de fuerza iónica total (TISAB) mezclando 500 mL de agua, 57 mL de ácido acético glacial, 58 g de NaCl y 4 g de DCTA disódico (ácido trans-1,2-ciclohexanotetraacético) en un vaso de precipitados de 1 L, agitando hasta que se disuelva. Enfriar el vaso de precipitados en un baño de agua y agregar NaOH 5 M hasta que el pH esté entre 5—5.5. Transfiera el contenido del vaso de precipitados a un matraz aforado de 1 l y diluya al volumen. Prepare cada estándar externo colocando aproximadamente 1 g de una pasta de dientes sin flúor, 30 mL de agua destilada y 1.00 mL de estándar en un vaso de precipitados de plástico de 50 mL y mezcle vigorosamente durante dos min con una barra agitadora. Transferir cuantitativamente la suspensión resultante a un matraz aforado de 100 mL junto con 50 mL de TISAB y diluir a volumen con agua destilada. Almacene todo el estándar externo en un vaso de precipitados de plástico de 250 ml hasta que esté listo para medir el potencial. Prepare muestras de pasta de dientes obteniendo una porción de aproximadamente 1 g y tratando de la misma manera que los estándares. Mida el potencial celular para los estándares externos y las muestras usando un electrodo selectivo de iones F y un electrodo de referencia apropiado. Al medir el potencial, revuelva la solución y deje de dos a tres minutos para alcanzar un potencial estable. Reporte la concentración de F — en la pasta de dientes %w/w SnF 2.
Preguntas
1. El tampón de ajuste de la fuerza iónica total sirve para varios propósitos en este procedimiento. Identificar estos fines.
La composición del TISAB tiene tres propósitos:
(a) La alta concentración de NaCl (las soluciones finales son aproximadamente 1 M de NaCl) asegura que la fuerza iónica de cada patrón externo y cada muestra es esencialmente idéntica. Debido a que el coeficiente de actividad del fluoruro es el mismo en todas las soluciones, podemos escribir la ecuación de Nernst en términos de concentración de fluoruro en lugar de su actividad.
b) La combinación de ácido acético glacial y NaOH crea un tampón ácido acético/acetato de pH 5—5.5. Como se muestra en la Figura 11.2.17 , el pH de este tampón es lo suficientemente alto como para asegurar que la forma predominante de fluoruro es F — en lugar de HF. Este pH también es suficientemente ácido como para evitar una interferencia del OH — (ver Ejemplo\(\PageIndex{8)}\)).
(c) Se agrega DCTA como agente complejante para Fe 3 + o Al 3 +, evitando la formación de\(\text{FeF}_6^{3-}\) o\(\text{AlF}_6^{3-}\).
2. ¿Por qué se agrega una pasta de dientes sin flúor a las soluciones estándar?
Agregar una pasta de dientes libre de flúor protege contra cualquier efecto de matriz no contabilizado que pueda influir en la respuesta del electrodo selectivo de iones. Esto supone, por supuesto, que las matrices de las dos pastas dentales son por lo demás similares.
3. El procedimiento especifica que los estándares y la muestra deben almacenarse en recipientes de plástico. ¿Por qué es una mala idea almacenar las soluciones en envases de vidrio?
El ion fluoruro es capaz de reaccionar con el vidrio para formar SiF 4.
4. Supongamos que su curva de calibración tiene una pendiente de —57.98 mV por cada cambio de 10 veces en la concentración de F —. La pendiente ideal de la ecuación de Nernst es —59.16 mV por cambio de concentración de 10 veces. ¿Qué efecto tiene esto en el análisis cuantitativo de fluoruro en pasta de dientes?
¡Ningún efecto en absoluto! Es por ello que preparamos una curva de calibración utilizando múltiples estándares.
Medición del pH
Con la disponibilidad de electrodos de pH de vidrio de bajo costo y medidores de pH, la determinación del pH es una de las mediciones analíticas cuantitativas más comunes. La determinación potenciométrica del pH, sin embargo, no está exenta de complicaciones, varias de las cuales discutimos en esta sección.
Una complicación es la confusión sobre el significado del pH [Kristensen, H. B.; Saloman, A.; Kokholm, G. Anal. Chem. 1991, 63, 885A—891A]. La definición convencional de pH en la mayoría de los libros de texto de química general es
\[\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right] \label{11.17}\]
Como ahora sabemos, el pH en realidad es una medida de la actividad de H +.
\[\mathrm{pH}=-\log a_{\mathrm{H}^{+}} \label{11.18}\]
Pruebe este experimento: encuentre varios libros de texto de química general y busque el pH en el índice de cada libro de texto. Diríjase a las páginas correspondientes y vea cómo se define. A continuación, busque actividad o coeficiente de actividad en el índice de cada libro de texto y vea si estos términos están indexados.
La ecuación\ ref {11.17} solo se aproxima al pH verdadero. Si calculamos el pH de HCl 0.1 M usando la Ecuación\ ref {11.17}, obtenemos un valor de 1.00; el pH real de la solución, definido por la Ecuación\ ref {11.18}, es 1.1 [Hawkes, S. J. J. Chem. Educ. 1994, 71, 747—749]. La actividad y la concentración de H + no son las mismas en HCl 0.1 M porque el coeficiente de actividad para H + no es 1.00 en esta matriz. La Figura 11.2.18 muestra una demostración más colorida de la diferencia entre actividad y concentración.

Una segunda complicación en la medición del pH es la incertidumbre en la relación entre potencial y actividad. Para un electrodo de membrana de vidrio, el potencial celular, (celda E) samp, para una muestra de pH desconocido es
donde K incluye el potencial del electrodo de referencia, el potencial de asimetría de la membrana de vidrio y cualquier potencial de unión en la celda electroquímica. Todas las contribuciones a K están sujetas a incertidumbre, y pueden cambiar del día a día, así como de electrodo a electrodo. Por esta razón, antes de usar un electrodo de pH lo calibramos usando un tampón estándar de pH conocido. El potencial celular para el estándar, (celda E) std, es
donde pH std es el pH del estándar. Restar la ecuación\ ref {11.20} de la ecuación\ ref {11.19} y resolviendo para pH samp da
que es la definición operativa de pH adoptada por la Unión Internacional de Química Pura y Aplicada [Covington, A. K.; Bates, R. B.; Durst, R. A. Pure & Appl. Chem. 1985, 57, 531—542].
Calibrar un electrodo de pH presenta una tercera complicación porque necesitamos un estándar con una actividad conocida con precisión para H +. El cuadro 11.2.6 proporciona valores de pH para varias soluciones tampón estándar primarias aceptadas por el Instituto Nacional de Estándares y Tecnología.
Para estandarizar un electrodo de pH usando dos tampones, elija uno cercano a un pH de 7 y otro que sea más ácido o básico dependiendo del pH esperado de su muestra. Enjuague su electrodo de pH en agua desionizada, séquelo con una toallita de laboratorio y colóquelo en el tampón con el pH más cercano a 7. Gira el electrodo de pH y deja que se equilibre hasta obtener una lectura estable. Ajuste la perilla “Estandarizar” o “Calibrar” hasta que el medidor muestre el pH correcto. Enjuague y seque el electrodo, y colóquelo en el segundo tampón. Después de que el electrodo se equilibre, ajuste la perilla “Pendiente” o “Temperatura” hasta que el medidor muestre el pH correcto.
Algunos medidores de pH pueden compensar un cambio de temperatura. Para utilizar esta característica, coloque una sonda de temperatura en la muestra y conéctela al medidor de pH. Ajuste el botón “Temperatura” a la temperatura de la solución y calibra el medidor de pH usando los controles “Calibrar” y “Pendiente”. Al usar el electrodo de pH, el medidor de pH compensa cualquier cambio en la temperatura de la muestra ajustando la pendiente de la curva de calibración usando una respuesta nernstiana de 2.303 RT/F.
Aplicaciones Clínicas
Debido a su selectividad para analitos en matrices complejas, los electrodos selectivos de iones son sensores importantes para muestras clínicas. Los analitos más comunes son los electrolitos, como Na +, K +, Ca 2+, H + y Cl —, y los gases disueltos como el CO 2. Para los fluidos extracelulares, como la sangre y la orina, el análisis se puede hacer in vitro. Un análisis in situ, sin embargo, requiere un electrodo mucho más pequeño que podamos insertar directamente en una celda. Los microelectrodos de membrana de base líquida con diámetros de punta menores a 1 μm se construyen calentando y estirando un tubo capilar de vidrio duro con un diámetro inicial de aproximadamente 1—2 mm (Figura 11.2.19 ). La punta del microelectrodo se hace hidrófoba sumergiéndola en una solución de diclorodimetil silano, y una solución interna apropiada para el analito y un electrodo de referencia de alambre de Ag/AgCl se colocan dentro del microelectrodo. El microelectrodo se sumerge en una solución del agente complejante líquido, que a través de la acción capilar atrae un pequeño volumen del agente complejante líquido hacia la punta. Se han desarrollado microelectrodos potenciométricos para una serie de analitos clínicamente importantes, incluyendo H +, K +, Na +, Ca 2+, Cl —, e I — [Bakker, E.; Pretsch, E. Trends Anal. Chem. 2008, 27, 612—618].
Aplicaciones Ambientales
Si bien los electrodos selectivos de iones se utilizan en el análisis ambiental, su aplicación no está tan extendida como en el análisis clínico. Aunque existen métodos potenciométricos estándar para el análisis de CN —, F —, NH 3 y\(\text{NO}_3^-\) en agua y aguas residuales, otros métodos analíticos generalmente proporcionan mejores límites de detección. Una ventaja potencial de un electrodo selectivo de iones es la capacidad de incorporarlo en una celda de flujo para el monitoreo continuo de corrientes de aguas residuales.
Titulaciones Potenciométricas
Un método para determinar el punto de equivalencia de una titulación ácido-base es usar un electrodo de pH para monitorear el cambio en el pH durante la titulación. Una determinación potenciométrica del punto de equivalencia es posible para valoraciones ácido-base, complejación, redox y precipitación, así como para valoraciones en disolventes acuosos y no acuosos. Las valoraciones potenciométricas ácido-base, complejación y precipitación generalmente se monitorean con un electrodo selectivo de iones que responde al analito, aunque también se puede usar un electrodo que responda al valorante o un producto de reacción. Un electrodo redox, como un cable de Pt, y un electrodo de referencia se utilizan para las titulaciones redox potenciométricas. Más detalles sobre las titulaciones potenciométricas se encuentran en el Capítulo 9.
Evaluación
Escala de Operación
El rango de trabajo para la mayoría de los electrodos selectivos de iones es de una concentración máxima de 0.1—1 M a una concentración mínima de\(10^{-5}-10^{-11}\) M [(a) Bakker, E.; Pretsch, E. Anal. Chem. 2002, 74, 420A-426A; b) Bakker, E.; Pretsch, E. Tendencias Anal. Chem. 2005, 24, 199—207]. Este amplio rango de trabajo se extiende desde analitos principales hasta analitos de ultratraza, y es significativamente mayor que muchas otras técnicas analíticas. Para usar un electrodo selectivo de iones convencional necesitamos un volumen de muestra mínimo de varios mL (una macro muestra). Los microelectrodos, como el que se muestra en la Figura 11.2.19 , se utilizan con una muestra ultramicro, aunque es necesario tener cuidado para asegurar que la muestra sea representativa de la muestra original.
Precisión
La precisión de un análisis potenciométrico está limitada por el error en la medición de la celda E. Varios factores contribuyen a este error de medición, incluyendo la contribución al potencial de iones interferentes, la corriente finita que pasa a través de la célula mientras medimos el potencial, las diferencias entre el coeficiente de actividad del analito en las muestras y las soluciones estándar, y la unión potenciales. Podemos limitar el efecto de un ion interferente incluyendo una etapa de separación antes del análisis potenciométrico. Los potenciómetros modernos de alta impedancia minimizan la cantidad de corriente que pasa a través de la celda electroquímica. Finalmente, podemos minimizar los errores debidos a los coeficientes de actividad y potenciales de unión al hacer coincidir la matriz de los estándares con la de la muestra. Incluso en las mejores circunstancias, sin embargo, no es inusual una diferencia de aproximadamente ±1 mV para muestras con concentraciones iguales de analito.
Podemos evaluar el efecto de la incertidumbre sobre la precisión de una medición potenciométrica mediante el uso de una propagación de la incertidumbre. Para un electrodo selectivo de iones de membrana, la expresión general de potencial es
\[E_{\mathrm{cell}}=K+\frac{R T}{z F} \ln \left[ A\right] \nonumber\]
donde z es la carga del analito, A,. Del Cuadro 4.3.1 del Capítulo 4, la incertidumbre en el potencial celular,\(\Delta E_\text{cell}\) es
\[\triangle E_{\text {cell}}=\frac{R T}{z F} \times \frac{\Delta [A]}{[A]} \nonumber\]
Reorganizar y multiplicar por 100 da el porcentaje de error relativo en la concentración como
El error relativo en la concentración, por lo tanto, es una función del error de medición para el potencial del electrodo\(\Delta E_\text{cell}\), y la carga del analito. La Tabla 11.2.7 proporciona valores representativos para iones con cargas de ±1 y ±2 a una temperatura de 25 o C. Las precisiones del 1— 5% para los iones monovalentes y del 2— 10% para los iones divalentes son típicas. Aunque la Ecuación\ ref {11.22} se aplica a los electrodos de membrana, podemos usar si para un electrodo metálico reemplazando z por n.
Precisión
La precisión en la potenciometría está limitada por las variaciones en la temperatura y la sensibilidad del potenciómetro. Bajo la mayoría de las condiciones, y cuando se usa un potenciómetro simple de propósito general, podemos medir el potencial con una repetibilidad de ±0.1 mV. Usando la Tabla 11.2.7 , esto corresponde a una incertidumbre de ± 0.4% para analitos monovalentes y ± 0.8% para analitos divalentes. La reproducibilidad de las mediciones potenciométricas es aproximadamente un factor de diez más pobres.
Sensibilidad
La sensibilidad de un análisis potenciométrico está determinada por el término RT/nF o RT/zF en la ecuación de Nernst. La sensibilidad es mejor para valores más pequeños de n o z.
Selectividad
Como se describió anteriormente, la mayoría de los electrodos selectivos de iones responden a más de un analito; la selectividad para el analito, sin embargo, a menudo es significativamente mayor que la sensibilidad para los iones interferentes. El fabricante de un selectivo de iones suele proporcionar coeficientes de selectividad de ISE, lo que nos permite determinar si un análisis potenciométrico es factible para una muestra determinada.
Tiempo, Costo y Equipo
En comparación con otras técnicas, la potenciometría proporciona un medio rápido, relativamente bajo costo para analizar muestras. El factor limitante al analizar un gran número de muestras es la necesidad de enjuagar el electrodo entre muestras. El uso de electrodos selectivos de iones desechables y económicos puede aumentar el rendimiento de muestras de un laboratorio. La figura 11.2.20 muestra un ejemplo de un ISE desechable para Ag + [Tymecki, L.; Zwierkowska, E.; Głab, S.; Koncki, R. Sens. Actuadores B 2003, 96, 482—488]. Los instrumentos comerciales para medir el pH o el potencial están disponibles en una variedad de rangos de precios, e incluyen modelos portátiles para su uso en el campo.