11.3: Métodos culométricos

En un método potenciométrico de análisis determinamos la concentración de un analito midiendo el potencial de una celda electroquímica bajo condiciones estáticas en las que no fluye corriente y las concentraciones de especies en la celda electroquímica permanecen fijas. Las técnicas dinámicas, en las que la corriente pasa a través de la celda electroquímica y cambian las concentraciones, también son importantes métodos electroquímicos de análisis. En esta sección consideramos la coulometría. La voltametría y la amperometría están cubiertas en el Capítulo 11.4.

La culometría se basa en una electrólisis exhaustiva del analito. Por exhaustivo queremos decir que el analito se oxida o se reduce completamente en el electrodo de trabajo, o que reacciona completamente con un reactivo generado en el electrodo de trabajo. Hay dos formas de culometría: la culombiometría de potencial controlado, en la que aplicamos un potencial constante a la celda electroquímica, y la culometría de corriente controlada, en la que pasamos una corriente constante a través de la celda electroquímica.

Durante una electrólisis, la carga total, Q, en culombios, que pasa a través de la celda electroquímica es proporcional a la cantidad absoluta de analito según la ley de Faraday

\[Q=n F N_{A} \label{11.1}\]

donde n es el número de electrones por mol de analito, F es la constante de Faraday (96 487 C mol ^—1) y N _A son los moles de analito. Un culombo es equivalente a un A•seg; así, para una corriente constante, i, la carga total es

\[Q=i t_{e} \label{11.2}\]

donde t _e es el tiempo de electrólisis. Si la corriente varía con el tiempo, como lo hace en la coulometría de potencial controlado, entonces la carga total es

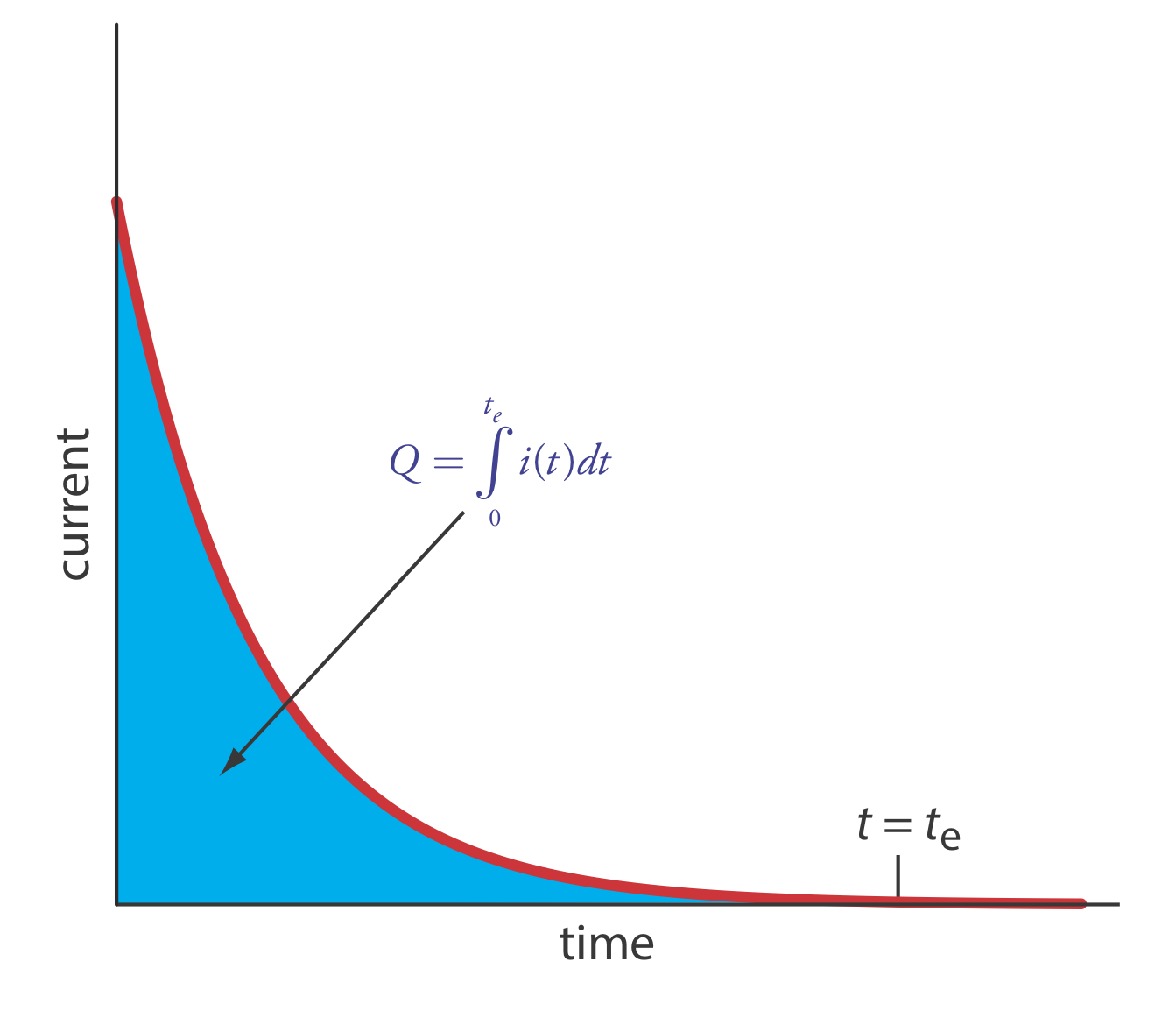
\[Q=\int_{0}^{t_e} i(t) d t \label{11.3}\]

En coulometría, monitoreamos la corriente en función del tiempo y usamos la Ecuación\ ref {11.2} o la Ecuación\ ref {11.3} para calcular Q. Conociendo la carga total, entonces usamos la Ecuación\ ref {11.1} para determinar los moles de analito. Para obtener un valor exacto para N _A, toda la corriente debe oxidar o reducir el analito; es decir, la culometría requiere 100% de eficiencia de corriente o una medición precisa de la eficiencia de corriente usando un estándar.

La eficiencia de la corriente es el porcentaje de corriente que realmente conduce a la oxidación o reducción del analito.

Coulometría de Potencial Controlado

La manera más fácil de asegurar una eficiencia de corriente del 100% es mantener el electrodo de trabajo a un potencial constante donde el analito se oxida o se reduce por completo y donde no se oxidan o reducen las especies potenciales interferentes. A medida que avanza la electrólisis, la concentración del analito y la corriente disminuyen. El perfil de corriente contra tiempo resultante para la culometría de potencial controlado se muestra en la Figura 11.3.1 . Integrar el área bajo la curva (Ecuación\ ref {11.3}) de t = 0 a t = t _e da la carga total. En esta sección consideramos los parámetros experimentales y la instrumentación necesarios para desarrollar un método coulométrico de potencial controlado de análisis.

Figura 11.3.1 . Corriente versus tiempo para un análisis coulométrico de potencial controlado. La corriente medida se muestra por la curva roja. El área integrada bajo la curva, mostrada en azul, es la carga total.

Selección de un potencial constante

Para entender cómo se selecciona un potencial apropiado para el electrodo de trabajo, desarrollemos un método coulométrico de potencial constante para Cu ^{2 +} basado en su reducción a cobre metálico en un electrodo de trabajo de Pt.

\[\mathrm{Cu}^{2+}(a q)+2 e^{-} \rightleftharpoons \mathrm{Cu}(s) \label{11.4}\]

La Figura 11.3.2 muestra un diagrama de escalera para una solución acuosa de Cu ^{2 +}. Por el diagrama de escalera sabemos que la reacción\ ref {11.4} se ve favorecida cuando el potencial del electrodo de trabajo es más negativo que +0.342 V frente al electrodo de hidrógeno estándar. Para asegurar una eficiencia de corriente del 100%, sin embargo, el potencial debe ser suficientemente más positivo que +0.000 V para que la reducción de H ₃ O ⁺ a H ₂ no contribuya significativamente a que la corriente total fluya a través de la celda electroquímica.

Figura 11.3.2 . Diagrama en escalera para una solución acuosa de Cu ²⁺ mostrando escalones para las reducciones de O ₂ a H ₂ O, de Cu ^{2 +} a Cu, y de H ₃ O ⁺ a H ₂. Para cada paso, la especie oxidada está en azul y la especie reducida está en rojo

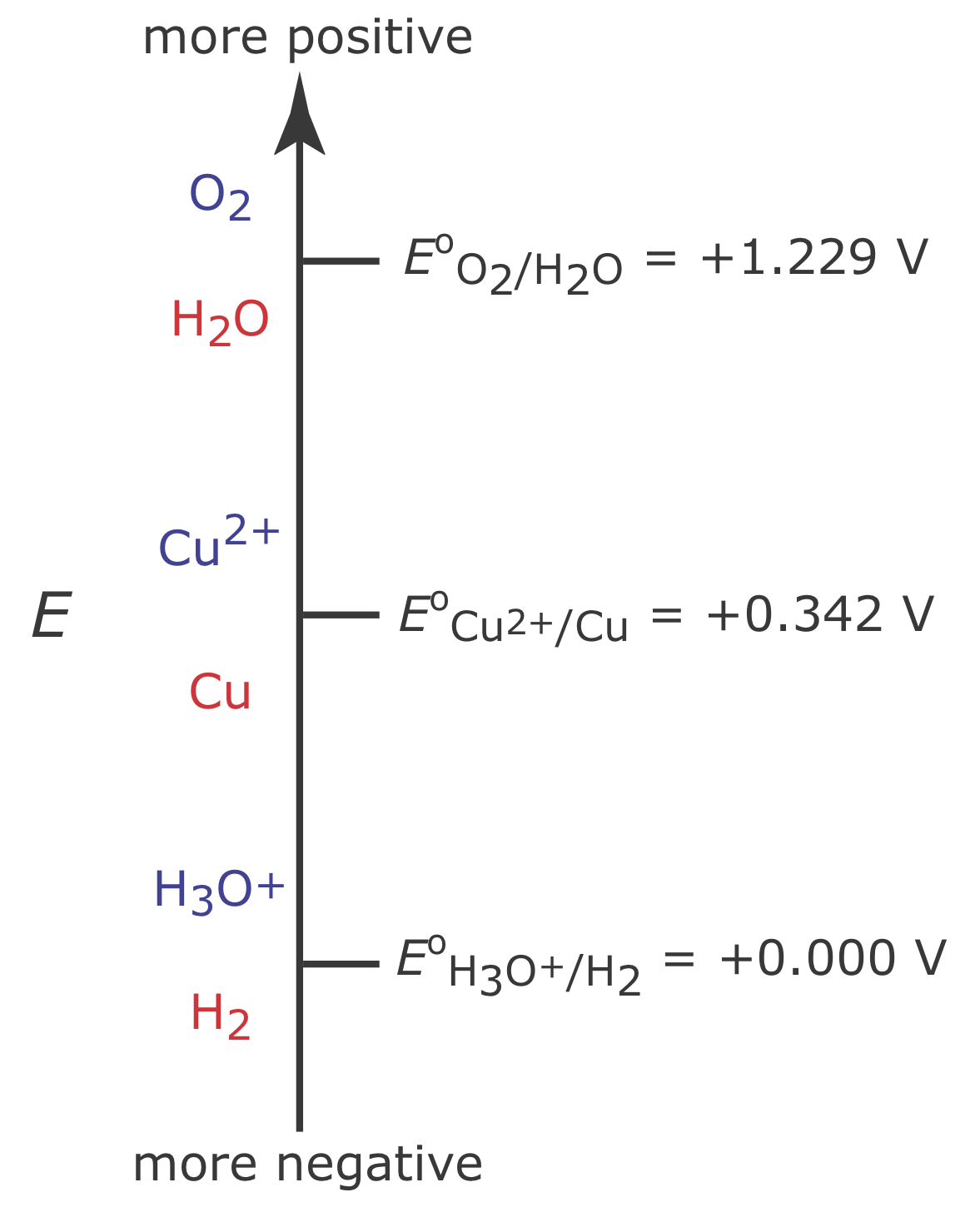
Podemos usar la ecuación de Nernst para reacción\ ref {11.4} para estimar el potencial mínimo para reducir cuantitativamente Cu ^{2 +}.

\[E=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\mathrm{o}}-\frac{0.05916}{2} \log \frac{1}{\left[\mathrm{Cu}^{2+}\right]} \label{11.5}\]

Entonces, ¿por qué estamos usando la concentración de Cu ^{2 +} en la Ecuación\ ref {11.5} en lugar de su actividad? En potenciometría utilizamos actividad porque utilizamos _células E para determinar la concentración del analito. Aquí utilizamos la ecuación de Nernst para ayudarnos a seleccionar un potencial apropiado. Una vez que identificamos un potencial, podemos ajustar su valor según sea necesario para asegurar una reducción cuantitativa de Cu ^{2 +}. Además, en coulometría la concentración del analito viene dada por la carga total, no por el potencial aplicado.

Si definimos una electrólisis cuantitativa como aquella en la que reducimos 99.99% de ^Cu2+ a Cu, entonces la concentración de Cu ²⁺ a t _e es

\[\left[\mathrm{Cu}^{2+}\right]_{t_{e}}=0.0001 \times\left[\mathrm{Cu}^{2+}\right]_{0} \label{11.6}\]

donde [Cu ^{2 +}] ₀ es la concentración inicial de Cu ^{2 +} en la muestra. Sustituir la Ecuación\ ref {11.6} por la Ecuación\ ref {11.5} nos permite calcular el potencial deseado.

\[E=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\circ}-\frac{0.05916}{2} \log \frac{1}{0.0001 \times\left[\mathrm{Cu}^{2+}\right]} \nonumber\]

Si la concentración inicial de Cu ²⁺ es\(1.00 \times 10^{-4}\) M, por ejemplo, entonces el potencial del electrodo de trabajo debe ser más negativo que +0.105 V para reducir cuantitativamente Cu ^{2 +} a Cu. Tenga en cuenta que a este potencial H ₃ O ⁺ no se reduce a H ₂, manteniendo el 100% de eficiencia de corriente.

Muchos métodos coulométricos de potencial controlado para Cu ^{2 +} utilizan un potencial negativo en relación con el electrodo de hidrógeno estándar; véase, por ejemplo, Rechnitz, G. A. Controlled-Potential Analysis, Macmillan: New York, 1963, p.49. Con base en el diagrama de escalera en la Figura 11.3.2 podría esperar que aplicar un potencial <0.000 V reducirá parcialmente H ₃ O ⁺ a H ₂, resultando en una eficiencia de corriente inferior al 100%. La razón por la que podemos usar tal potencial negativo es que la velocidad de reacción para la reducción de H ₃ O ⁺ a H ₂ es muy lenta en un electrodo de Pt. Esto da como resultado un sobrepotencial significativo —la necesidad de aplicar un potencial más positivo o uno más negativo que el predicho por la termodinámica— que desplaza E ^o para la pareja redox H ₃ O ⁺ /H ₂ a una más negativa valor.

Minimización del tiempo de electró

En la coulometría de potencial controlado, como se muestra en la Figura 11.3.1 , la corriente disminuye con el tiempo. Como resultado, la tasa de electrólisis —recordar del Capítulo 11.1 que la corriente es una medida de la velocidad— se vuelve más lenta y una electrólisis exhaustiva del analito puede requerir mucho tiempo. Debido a que el tiempo es una consideración importante a la hora de diseñar un método analítico, debemos considerar los factores que afectan el tiempo de análisis.

Podemos aproximar el cambio de la corriente en función del tiempo en la Figura 11.3.1 como decaimiento exponencial; así, la corriente en el tiempo t es

\[i_{t}=i_{0} e^{-k t} \label{11.7}\]

donde i ₀ es la corriente a t = 0 y k es una constante de velocidad que es directamente proporcional al área del electrodo de trabajo y la velocidad de agitación, y que es inversamente proporcional al volumen de solución. Para una electrólisis exhaustiva en la que oxidamos o reducimos 99.99% del analito, la corriente al final del análisis, t _e, es

\[i_{t_{e}} \leq 0.0001 \times i_{0} \label{11.8}\]

Sustituyendo la Ecuación\ ref {11.8} en Ecuación\ ref {11.7} y resolviendo para t _e da el tiempo mínimo para una electrólisis exhaustiva como

\[t_{e}=-\frac{1}{k} \times \ln (0.0001)=\frac{9.21}{k} \nonumber\]

A partir de esta ecuación vemos que un valor mayor para k reduce el tiempo de análisis. Por esta razón, solemos realizar un análisis coulométrico de potencial controlado en una celda electroquímica de pequeño volumen, utilizando un electrodo con una gran superficie y con una alta velocidad de agitación. Una electrólisis cuantitativa normalmente requiere aproximadamente 30—60 min, aunque son posibles tiempos más cortos o más largos.

Instrumentación

Se utiliza un potenciostato de tres electrodos para establecer el potencial en la coulometría de potencial controlado (ver Figura 11.1.5). Los electrodos de trabajo suelen ser de dos tipos: un electrodo cilíndrico de Pt fabricado a partir de gasa de platino (Figura 11.3.3 ), o un electrodo de piscina de Hg. El gran sobrepotencial para la reducción de H ₃ O ⁺ a Hg lo convierte en el electrodo de elección para un analito que requiere un potencial negativo. Por ejemplo, un potencial más negativo que —1 V versus el SHE es factible en un electrodo de Hg, pero no en un electrodo de Pt, incluso en una solución muy ácida. Debido a que el mercurio es fácil de oxidar, es menos útil si necesitamos mantener un potencial que sea positivo con respecto a la ELE. El platino es el electrodo de trabajo de elección cuando necesitamos aplicar un potencial positivo.

Figura 11.3.3 . Ejemplo de un electrodo cilíndrico de gasa PT utilizado en la coulometría de potencial controlado. El electrodo que se muestra aquí tiene un diámetro de 13 mm y una altura de 48 mm, y fue conformado a partir de alambre de Pt con un diámetro de aproximadamente 0.15 mm. La superficie del electrodo tiene 360 aberturas/cm ² y una superficie total de aproximadamente 40 cm ².

El electrodo auxiliar, que a menudo es un cable de Pt, está separado por un puente de sal de la solución analítica. Esto es necesario para evitar que los productos de electrólisis generados en el electrodo auxiliar reaccionen con el analito e interfieran en el análisis. Un electrodo de calomel saturado o Ag/AgCl sirve como electrodo de referencia.

La otra necesidad esencial de coulometría de potencial controlado es un medio para determinar la carga total. Un método es monitorear la corriente en función del tiempo y determinar el área bajo la curva, como se muestra en la Figura 11.3.1 . Los instrumentos modernos utilizan la integración electrónica para monitorear la carga en función del tiempo. La carga total al final de la electrólisis se lee directamente de una lectura digital.

Electrogravimetría

Si el producto de la coulometría de potencial controlado forma un depósito en el electrodo de trabajo, entonces podemos usar el cambio en la masa del electrodo como señal analítica. Por ejemplo, si aplicamos un potencial que reduce Cu ^{2 +} a Cu en un electrodo de trabajo de Pt, la diferencia en la masa del electrodo antes y después de la electrólisis es una medición directa de la cantidad de cobre en la muestra. Como aprendimos en el Capítulo 8, llamamos a una técnica analítica que utiliza la masa como señal una técnica gravimétrica; así, llamamos a esta electrogravimetría.

Coulometría de corriente controlada

Un segundo enfoque de la cululometría es utilizar una corriente constante en lugar de un potencial constante, lo que da como resultado el perfil de corriente contra tiempo que se muestra en la Figura 11.3.4 . La culometría de corriente controlada tiene dos ventajas sobre la coulometría de potencial controlado. Primero, el tiempo de análisis es más corto porque la corriente no disminuye con el tiempo. Un tiempo de análisis típico para la coulometría de corriente controlada es inferior a 10 min, en comparación con aproximadamente 30—60 min para la culometría de potencial controlado. Segundo, debido a que la carga total simplemente es producto de corriente y tiempo (Ecuación\ ref {11.2}), no hay necesidad de integrar la curva actual-tiempo en la Figura 11.3.4 .

Figura 11.3.4 . Corriente versus tiempo para un análisis coulométrico de corriente controlada. La corriente medida se muestra por la curva roja. El área integrada bajo la curva, mostrada en azul, es la carga total.

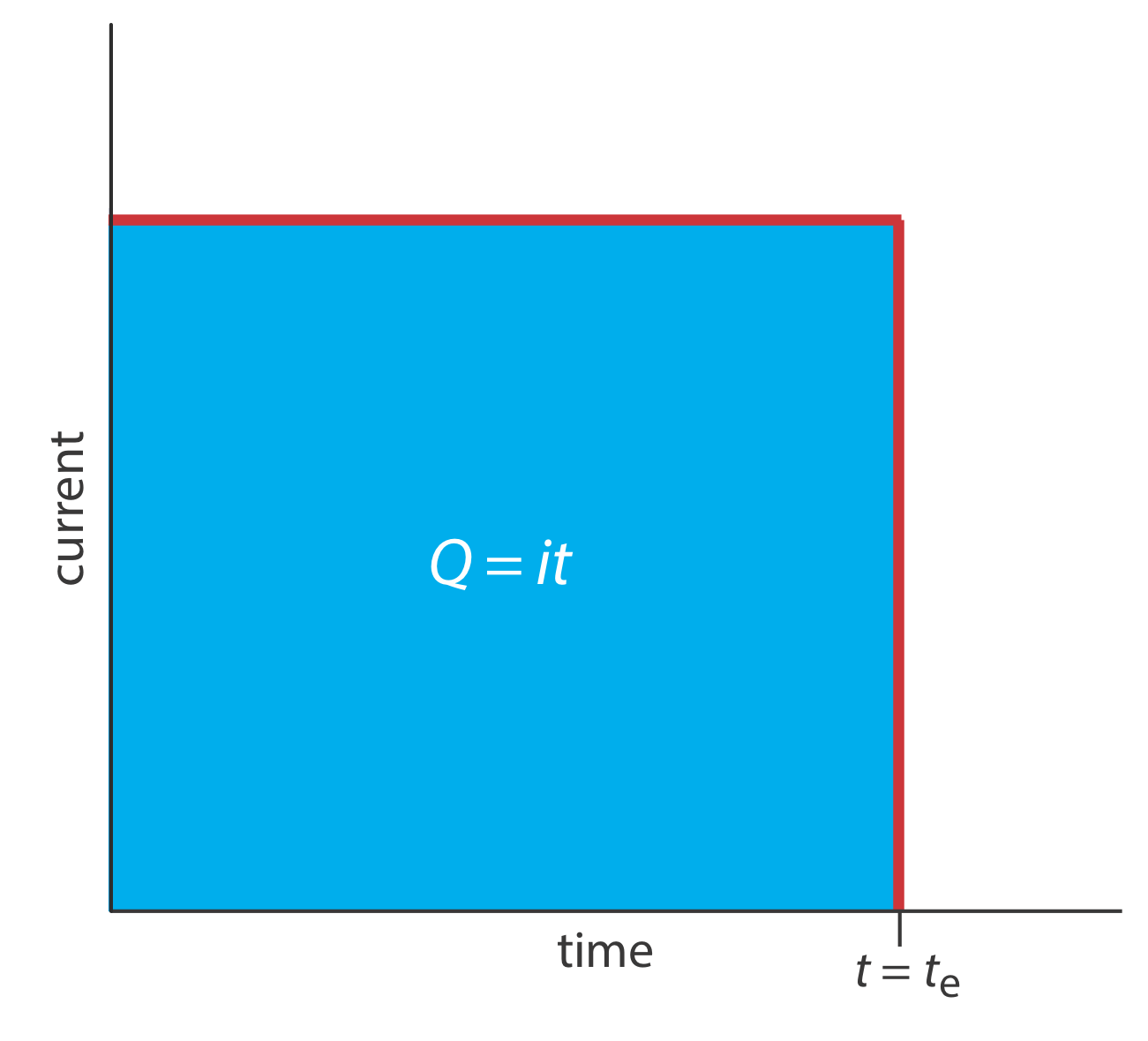
El uso de una corriente constante nos presenta dos problemas experimentales importantes. Primero, durante la electrólisis la concentración del analito y, por lo tanto, la corriente que resulta de su oxidación o reducción, disminuye continuamente. Para mantener una corriente constante debemos permitir que el potencial cambie hasta que ocurra otra reacción de oxidación o reacción de reducción en el electrodo de trabajo. A menos que diseñemos el sistema cuidadosamente, esta reacción secundaria da como resultado una eficiencia de corriente inferior al 100%. El segundo problema es que necesitamos un método para determinar cuándo se completa la electrólisis del analito. Como se muestra en la Figura 11.3.1 , en un análisis coulométrico de potencial controlado sabemos que la electrólisis se completa cuando la corriente alcanza cero, o cuando alcanza un fondo constante o corriente residual. En un análisis coulométrico de corriente controlada, sin embargo, la corriente continúa fluyendo incluso cuando la electrólisis del analito está completa. Se necesita un método adecuado para determinar el punto final de la reacción, t _e.

Mantenimiento de la eficiencia actual

Para ilustrar por qué un cambio en el potencial del electrodo de trabajo puede resultar en una eficiencia de corriente inferior al 100%, consideremos el análisis coulométrico para Fe ^{2 +} basado en su oxidación a Fe ^{3 +} en un electrodo de trabajo de Pt en 1 M H ₂ SO ₄.

\[\mathrm{Fe}^{2+}(a q) \rightleftharpoons \text{ Fe}^{3+}(a q)+e^{-} \nonumber\]

La Figura 11.3.5 muestra el diagrama de escalera para este sistema. Al inicio del análisis, el potencial del electrodo de trabajo permanece casi constante a un nivel cercano a su valor inicial.

Figura 11.3.5 . Diagrama en escalera para el análisis coulométrico de corriente constante de Fe ^{2 +}. La flecha roja y el texto muestran cómo el potencial deriva a valores más positivos, disminuyendo la eficiencia actual.

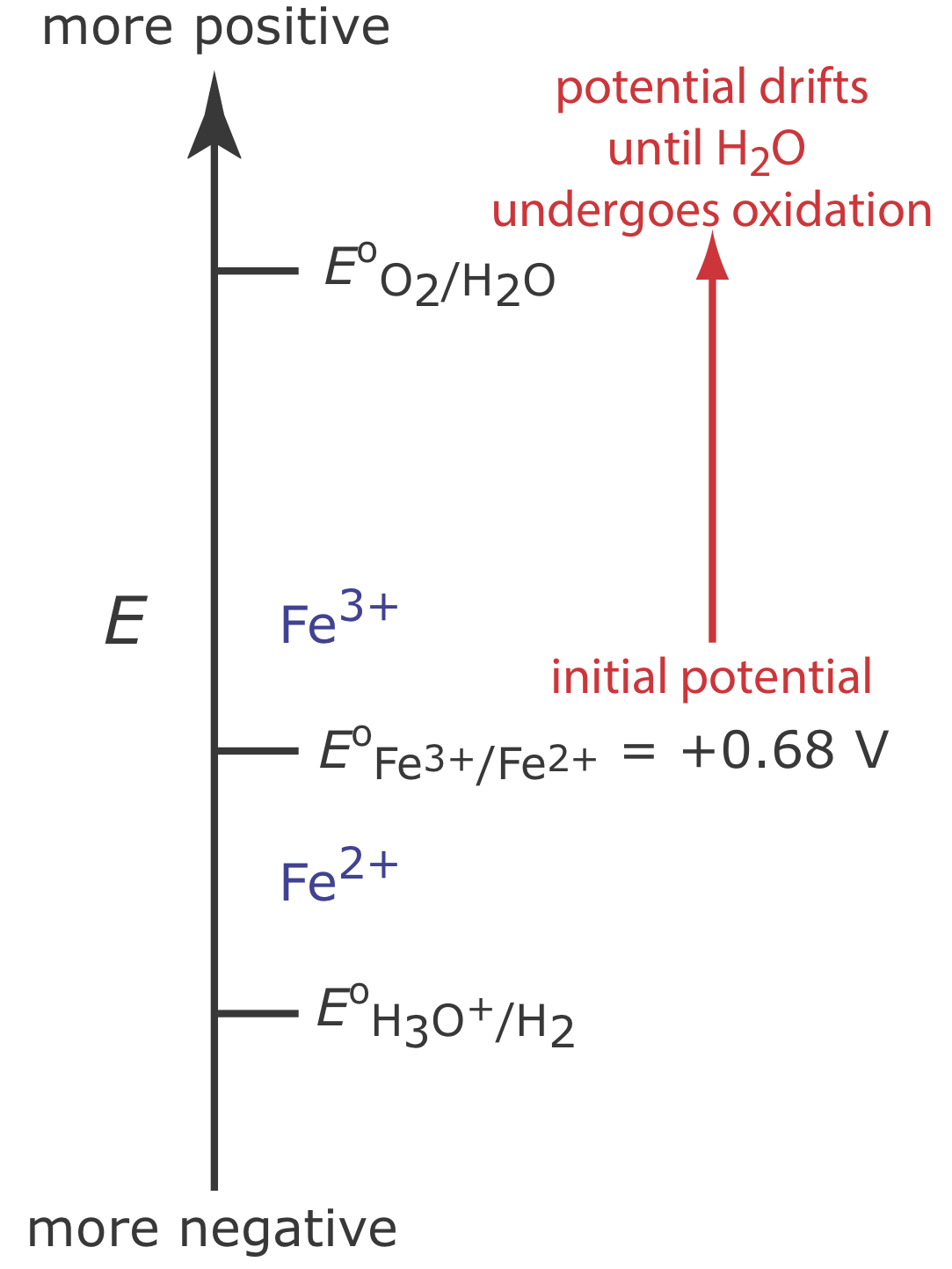
A medida que disminuye la concentración de Fe ^{2 +} y aumenta la concentración de Fe ^{3 +}, el potencial del electrodo de trabajo se desplaza hacia valores más positivos hasta que comienza la oxidación de H ₂ O.

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \text{ O}_{2}(g)+4 \mathrm{H}^{+}(a q)+4 e^{-} \nonumber\]

Debido a que una porción de la corriente total proviene de la oxidación de H ₂ O, la eficiencia de corriente para el análisis es inferior al 100% y no podemos usar la Ecuación\ ref {11.1} para determinar la cantidad de Fe ^{2 +} en la muestra.

Aunque no podemos evitar que el potencial se desvíe hasta que otra especie sufra oxidación, podemos mantener una eficiencia de corriente del 100% si el producto de esa reacción de oxidación secundaria reacciona rápida y cuantitativamente con el Fe ^{2 +} restante. Para lograrlo agregamos un exceso de Ce ^{3 +} a la solución analítica. Como se muestra en la Figura 11.3.6 , cuando el potencial del electrodo de trabajo cambia a un potencial más positivo, Ce ^{3 +} comienza a oxidarse a Ce ^{4 +}

\[\mathrm{Ce}^{3+}(a q) \rightleftharpoons \text{ Ce}^{4+}(a q)+e^{-} \label{11.9}\]

Figura 11.3.6 . Diagrama en escalera para el análisis coulométrico de corriente constante de Fe ^{2 +} en presencia de un mediador Ce ^{3 +}. A medida que el potencial deriva a valores más positivos, finalmente alcanzamos un potencial donde Ce ^{3 +} sufre oxidación. Debido a que Ce ^{4 +}, el producto de la oxidación de Ce ^{3 +}, reacciona con Fe ^{2 +}, mantenemos la eficiencia actual.

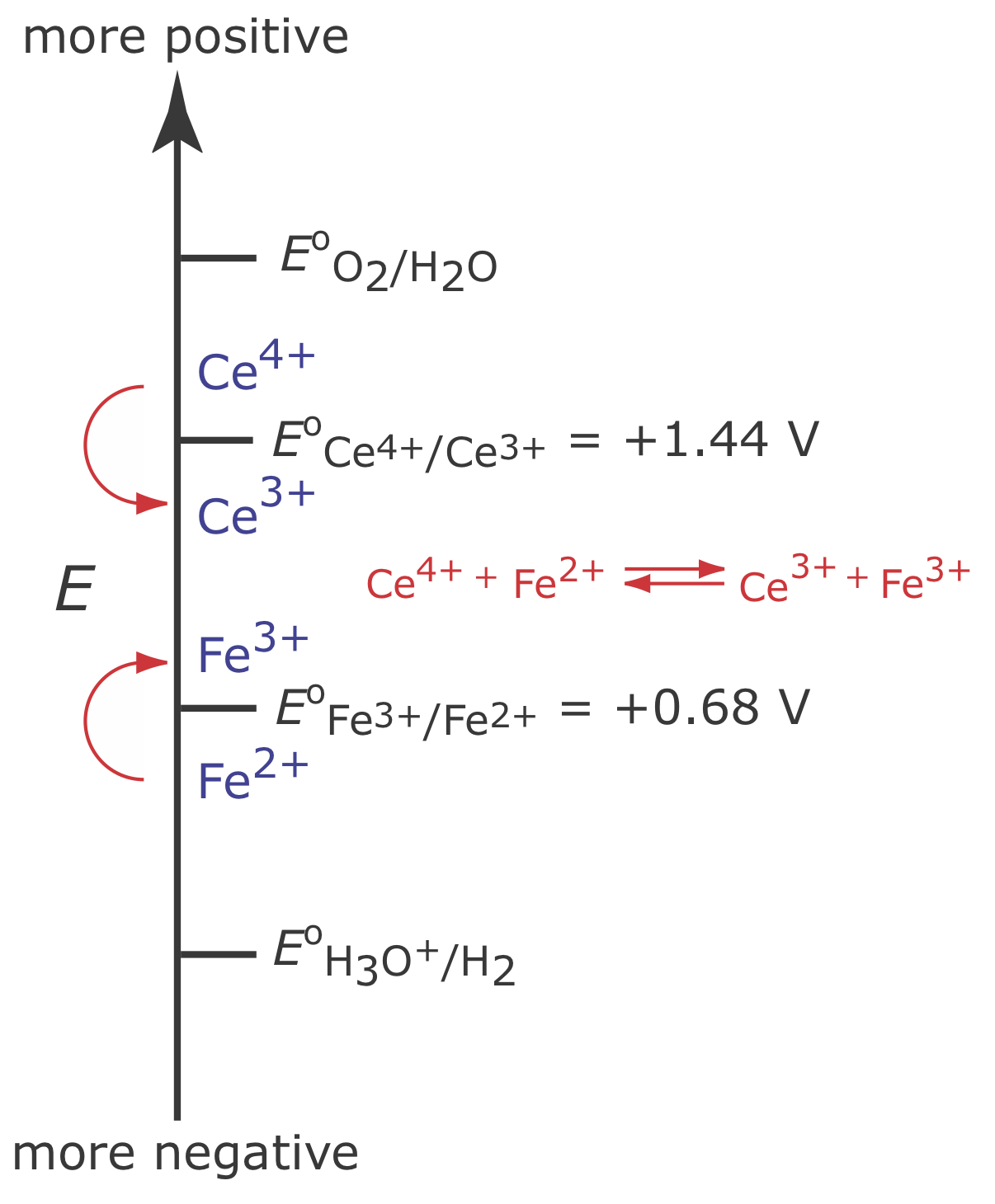
El Ce ^{4 +} que se forma en el electrodo de trabajo se mezcla rápidamente con la solución donde reacciona con cualquier Fe ^{2 +} disponible.

\[\mathrm{Ce}^{4+}(a q)+\text{ Fe}^{2+}(a q) \rightleftharpoons \text{ Ce}^{3+}(a q)+\text{ Fe}^{3+}(a q) \label{11.10}\]

Combinando la reacción\ ref {11.9} y la reacción\ ref {11.10} muestra que la reacción neta es la oxidación de Fe ^{2 +} a Fe ^{3 +}

\[\mathrm{Fe}^{2+}(a q) \rightleftharpoons \text{ Fe}^{3+}(a q)+e^{-} \nonumber\]

que mantiene una eficiencia actual del 100%. Una especie utilizada para mantener una eficiencia de corriente del 100% se llama mediador.

Determinación de punto final

Agregar un mediador resuelve el problema de mantener la eficiencia de corriente del 100%, pero no resuelve el problema de determinar cuándo se completa la electrólisis del analito. Utilizando el análisis para Fe ^{2 +} en la Figura 11.3.6 , cuando la oxidación de Fe ^{2 +} es completa la corriente continúa fluyendo de la oxidación de Ce ^{3 +}, y, eventualmente, la oxidación de H ₂ O. Lo que necesitamos es un señal que nos dice cuando no hay más Fe ^{2 +} presente en la solución.

Para nuestros propósitos, es conveniente tratar un análisis coulométrico de corriente controlada como una reacción entre el analito, Fe ^{2 +}, y el mediador, Ce ^{3 +}, como lo muestra la reacción\ ref {11.10}. Esta reacción es idéntica a una valoración redox; por lo tanto, podemos usar los puntos finales para una valoración redox (indicadores visuales y mediciones potenciométricas o conductométricas) para señalar el final de un análisis coulométrico de corriente controlada. Por ejemplo, la ferroína proporciona un punto final visual útil para el análisis coulométrico mediado por Ce ^{3 + para Fe 2 +}, cambiando de color de rojo a azul cuando se completa la electrólisis de Fe ^{2 +}.

La reacción\ ref {11.10} es la misma reacción que usamos en el Capítulo 9 para desarrollar nuestra comprensión de la titrimetría redox.

Instrumentación

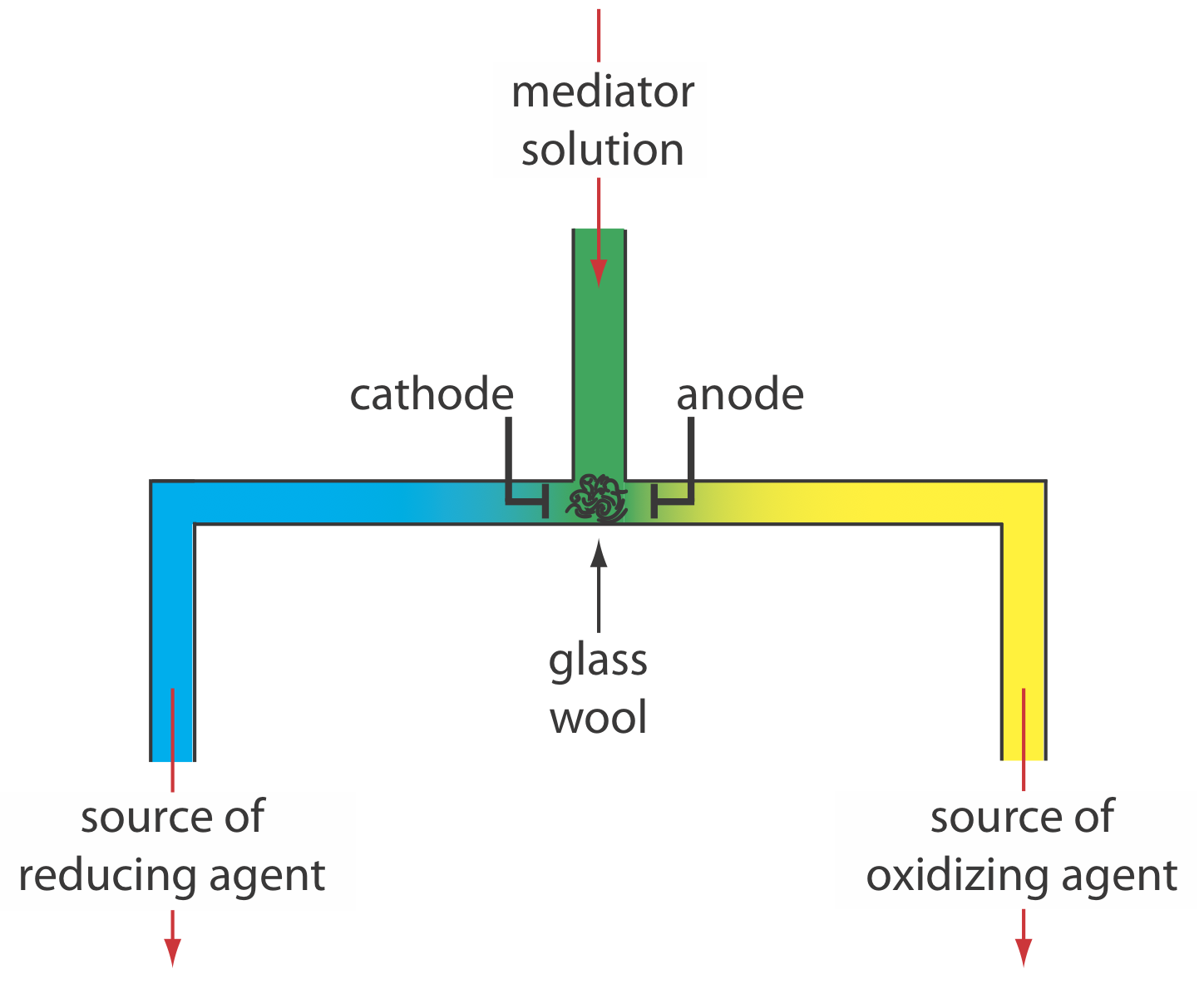
La coulometría de corriente controlada normalmente se lleva a cabo utilizando un galvanostato de dos electrodos, que consiste en un electrodo de trabajo y un contraelectrodo. El electrodo de trabajo, a menudo un simple electrodo de Pt, también se llama electrodo generador ya que es donde reacciona el mediador para generar la especie que reacciona con el analito. Si es necesario, el contraelectrodo se aísla de la solución analítica mediante un puente salino o una frita porosa para evitar que sus productos de electrólisis reaccionen con el analito. Alternativamente, podemos generar el agente oxidante o el agente reductor externamente, y permitir que fluya hacia la solución analítica. La figura 11.3.7 muestra un método simple para lograrlo. Una solución que contiene el mediador fluye hacia una celda electroquímica de pequeño volumen con los productos saliendo a través de tubos separados. Dependiendo del analito, el agente oxidante o el reactivo reductor se suministra a la solución analítica. Por ejemplo, podemos generar Ce ^{4 +} usando una solución acuosa de Ce ^{3 +}, dirigiendo el Ce ^{4 +} que se forma en el ánodo a nuestra muestra.

La Figura 11.1.4 muestra un ejemplo de un galvanostato manual. Aunque un galvanostato moderno utiliza circuitos muy diferentes, puede usar la Figura 11.1.4 y la discusión que la acompaña para entender cómo podemos usar el electrodo de trabajo y el contraelectrodo para controlar la corriente. La Figura 11.1.4 incluye un electrodo de referencia opcional, pero su presencia o ausencia no es importante si no estamos interesados en monitorear el potencial del electrodo de trabajo.

Figura 11.3.7 . Un ejemplo de un dispositivo para la generación externa de agentes oxidantes y reductores para coulometría de corriente controlada. Una solución que contiene el mediador fluye hacia una celda electroquímica de pequeño volumen. Los productos de oxidación resultantes, que se forman en el ánodo, fluyen hacia la derecha y sirven como agente oxidante. La reducción en el cátodo genera un agente reductor.

Hay otras dos necesidades cruciales para la coulometría de corriente controlada: un reloj preciso para medir el tiempo de electrólisis, t _e, y un interruptor para iniciar y detener la electrólisis. Un reloj analógico puede registrar el tiempo a los ±0.01 s más cercanos, pero la necesidad de detener e iniciar la electrólisis a medida que nos acercamos al punto final puede resultar en una incertidumbre general de ±0.1 s. Un reloj digital permite una medición más precisa del tiempo, con una incertidumbre general de ±1 ms. El interruptor debe controlar tanto la corriente como el reloj para que podamos hacer una determinación precisa del tiempo de electrólisis.

Titulaciones coulométricas

Un método coulométrico de corriente controlada a veces se denomina titulación coulométrica debido a su similitud con una titulación convencional. Por ejemplo, en el análisis coulométrico de corriente controlada para Fe ^{2 +} usando un mediador Ce ^{3 +}, la oxidación de Fe ^{2 +} por Ce ^{4 +} (reacción\ ref {11.10}) es idéntica a la reacción en una valoración redox.

Hay otras similitudes entre la culometría de corriente controlada y la titulación. Si combinamos la Ecuación\ ref {11.1} y la Ecuación\ ref {11.2} y resolvemos para los moles de analito, N _A, obtenemos la siguiente ecuación.

\[N_{A}=\frac{i}{n F} \times t_{e} \label{11.11}\]

Comparar la Ecuación\ ref {11.11} con la relación entre los moles de analito, N _A, y los moles de valorante, N _T, en una titulación

\[N_{A}=N_{T}=M_{T} \times V_{T} \nonumber\]

donde M _T y V _T son la molaridad del valorante y el volumen de valorante en el punto final. En la coulometría de corriente constante, la fuente de corriente es equivalente al valorante y el valor de esa corriente es análogo a la molaridad del valorante. El tiempo de electrólisis es análogo al volumen del valorante, y t _e es equivalente al punto final de la titulación a. Finalmente, el interruptor para iniciar y detener la electrólisis cumple la misma función que la llave de paso de una bureta.

Por simplicidad, asumimos anteriormente que la estequiometría entre el analito y el valorante es 1:1. La suposición, sin embargo, no es importante y no afecta nuestra observación de la similitud entre la culometría de corriente controlada y una titulación.

Aplicaciones Cuantitativas

La culometría se utiliza para el análisis cuantitativo de analitos tanto inorgánicos como orgánicos. Ejemplos de métodos coulométricos de potencial controlado y corriente controlada se discuten en las dos secciones siguientes.

Coulometría de Potencial Controlado

La mayoría de los análisis coulométricos de potencial controlado implican la determinación de cationes y aniones inorgánicos, incluyendo metales traza e iones haluros. Table 11.3.1 resume varios de estos métodos.

Tabla 11.3.1 . Análisis Cululométricos Representativos de Potencial Controlado para Iones Inorgánicos

analito	reacción electrolítica	electrodo
antimonio	\(\text{Sb}(\text{III}) + 3 e^{-} \rightleftharpoons \text{Sb}\)	Pt
arsénico	\(\text{As}(\text{III}) \rightleftharpoons \text{As(V)} + 2 e^{-}\)	Pt
cadmio	\(\text{Cd(II)} + 2 e^{-} \rightleftharpoons \text{Cd}\)	Pt o Hg
cobalto	\(\text{Co(II)} + 2 e^{-} \rightleftharpoons \text{Co}\)	Pt o Hg
cobre	\(\text{Cu(II)} + 2 e^{-} \rightleftharpoons \text{Cu}\)	Pt o Hg
halogenuros (X ^—)	\(\text{Ag} + \text{X}^- \rightleftharpoons \text{AgX} + e^-\)	Ag
hierro	\(\text{Fe(II)} \rightleftharpoons \text{Fe(III)} + e^-\)	Pt
plomo	\(\text{Pb(II)} + 2 e^{-} \rightleftharpoons \text{Pb}\)	Pt o Hg
níquel	\(\text{Ni(II)} + 2 e^{-} \rightleftharpoons \text{Ni}\)	Pt o Hg
plutonio	\(\text{Pu(III)} \rightleftharpoons \text{Pu(IV)} + e^-\)	Pt
plata	\(\text{Ag(I)} + 1 e^{-} \rightleftharpoons \text{Ag}\)	Pt
hojalata	\(\text{Sn(II)} + 2 e^{-} \rightleftharpoons \text{Sn}\)	Pt
uranio	\(\text{U(VI)} + 2 e^{-} \rightleftharpoons \text{U(IV})\)	Pt o Hg
zinc	\(\text{Zn(II)} + 2 e^{-} \rightleftharpoons \text{Zn}\)	Pt o Hg
Fuente: Rechnitz, G. A. Análisis de Potencial Controlado, Macmillan: Nueva York, 1963. Las reacciones electrolíticas se escriben en términos del cambio en el estado de oxidación del analito. La especie real en solución depende del analito.

La capacidad de controlar la selectividad ajustando el potencial del electrodo de trabajo hace que la culombimetría de potencial controlado sea particularmente útil para el análisis de aleaciones. Por ejemplo, podemos determinar la composición de una aleación que contiene Ag, Bi, Cd y Sb disolviendo la muestra y colocándola en una matriz de 0.2 M H ₂ SO ₄ junto con un electrodo de trabajo Pt y un contraelectrodo de Pt. Si aplicamos un potencial constante de +0.40 V frente al SCE, Ag (I) se deposita en el electrodo como Ag y los otros iones metálicos permanecen en solución. Cuando se completa la electrólisis, utilizamos la carga total para determinar la cantidad de plata en la aleación. A continuación, cambiamos el potencial del electrodo de trabajo a —0.08 V versus el SCE, depositando Bi en el electrodo de trabajo. Cuando se completa el análisis coulométrico para bismuto, determinamos el antimonio cambiando el potencial del electrodo de trabajo a —0.33 V versus el SCE, depositando Sb. Finalmente, determinamos cadmio después de su electrodeposición sobre el electrodo de trabajo a un potencial de —0.80 V frente al SCE.

También podemos utilizar la coulometría de potencial controlado para el análisis cuantitativo de compuestos orgánicos, aunque el número de aplicaciones es significativamente menor que el de los analitos inorgánicos. Un ejemplo es la reducción de seis electrones de un grupo nitro, —NO ₂, a una amina primaria, —NH ₂, en un electrodo de mercurio. Se analizan soluciones de ácido pícrico, también conocido como 2,4,6-trinitrofenol, o TNP, un pariente cercano del TNT, reduciéndolo a triaminofenol.

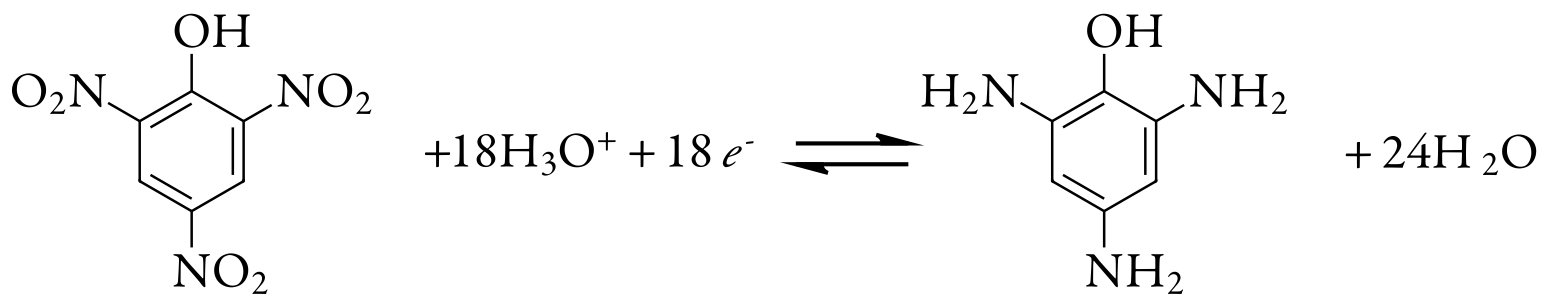
Otro ejemplo es la reducción sucesiva de tricloroacetato a dicloroacetato, y de dicloroacetato a monocloroacetato

\[\text{Cl}_3\text{CCOO}^-(aq) + \text{H}_3\text{O}^+(aq) + 2 e^- \rightleftharpoons \text{Cl}_2\text{HCCOO}^-(aq) + \text{Cl}^-(aq) + \text{H}_2\text{O}(l) \nonumber\]

\[\text{Cl}_2\text{HCCOO}^-(aq) + \text{ H}_3\text{O}^+(aq) + 2 e^- \rightleftharpoons \text{ ClH}_2\text{CCOO}^-(aq) + \text{ Cl}^-(aq) + \text{H}_2\text{O}(l) \nonumber\]

Podemos analizar una mezcla de tricloroacetato y dicloroacetato seleccionando un potencial inicial donde solo reacciona el tricloroacetato más fácilmente reducido. Cuando se completa su electrólisis, podemos reducir el dicloroacetato ajustando el potencial a un potencial más negativo. La carga total para la primera electrólisis da la cantidad de tricloroacetato, y la diferencia en la carga total entre la primera electrólisis y la segunda electrólisis da la cantidad de dicloroacetato.

Coulometría de Corriente Controlada (Titulación Coulométrica)

El uso de un mediador hace que la valoración culombimétrica sea una técnica analítica más versátil que la coulometría de potencial controlado. Por ejemplo, la oxidación o reducción directa de una proteína en un electrodo de trabajo es difícil si el sitio redox activo de la proteína se encuentra profundamente dentro de su estructura. Una titulación coulométrica de la proteína es posible, sin embargo, si utilizamos la oxidación o reducción de un mediador para producir una especie de solución que reaccione con la proteína. El cuadro 11.3.2 resume varios métodos culombimétricos de corriente controlada basados en una reacción redox utilizando un mediador.

Tabla 11.3.2 . Ejemplos Representativos de Titulaciones Coulométricas Redox

mediador	reactivo generado electroquímicamente y reacción	aplicación representativa
Ag ^+	\(\mathrm{Ag}^{+} \rightleftharpoons \textbf{Ag}^\textbf{2+}+e^{-}\)	\ (\ mathbf {H} _ {2}\ mathbf {C} _ {2}\ mathbf {O} _ {4} (a q) +2\ mathrm {Ag} ^ {2+} (a q) +2\ mathrm {H} _ {2}\ mathrm {O} (l)\ rightleftharpoons\\ 2\ text {CO} _2 (g) + 2\ texto {Ag} ^+ (aq) + 2\ texto {H} _3\ texto {O} ^+ (aq)\)
Br ^—	\(2\mathrm{Br}^{-} \rightleftharpoons \textbf{Br}_\textbf{2}+2 e^{-}\)	\ (\ textbf {H} _\ textbf {2}\ textbf {S} (a q) +\ text {Br} _ {2} (\ mathrm {aq}) +2\ mathrm {H} _ _ {2}\ mathrm {O} (\ mathrm {l})\ rightleftharpoons\ \ text {S} (s) + 2\ text {Br} ^- (aq) + 2\ texto {H} _3\ texto {O} ^+ (aq)\)
Ce ^3+	\(\mathrm{Ce}^{3+} \rightleftharpoons \textbf{Ce}^\textbf{4+}+e^{-}\)	\(\textbf{Fe}(\mathbf{C N})_\textbf{6}^\textbf{4–}(a q)+\text{ Ce}^{4+}(a q) \rightleftharpoons \\ \mathrm{Fe}(\mathrm{CN})_{6}^{3-}(a q)+\text{ Ce}^{3+}(a q)\)
Cl ^—	\(2\mathrm{Cl}^{-} \rightleftharpoons \textbf{Cl}_\textbf{2}+2 e^{-}\)	\(\textbf{Ti(I)}(a q)+\text{ Cl}_{2}(a q) \rightleftharpoons \mathrm{Ti}(\mathrm{III})(a q)+2 \mathrm{Cl}^{-}(a q)\)
Fe ^3+	\(\mathrm{Fe}^{3+} +e^{-} \rightleftharpoons \textbf{Fe}^\textbf{2+}\)	\ (\ mathbf {Cr} _\ textbf {2}\ mathbf {O} _\ textbf {7} ^\ mathbf {2-} (a q) +6\ mathrm {Fe} ^ {2+} (a q) +14\ mathrm {H} _ {3}\ mathrm {O} ^ {+} (a q)\ rightleftharpoons\\ 2\ texto {Cr} ^ {3+} (aq) + 6\ texto {Fe} ^ {3+} (aq) + 21\ texto {H} _2\ texto {O} (l)\)
I ^—	\(3\mathrm{I}^{-} \rightleftharpoons \textbf{I}_\textbf{3}^\textbf{–}+2 e^{-}\)	\(2 \mathbf{S}_\mathbf{2} \mathbf{O}_\mathbf{3}^\mathbf{2-}(a q)+\mathrm{I}_{3}^{-}(a q) \rightleftharpoons \text{S}_{4} \mathrm{O}_{6}^{2-}(a q)+3 \mathrm{I}^{-}(a q)\)
Mn ^2+	\(\mathrm{Mn}^{2+} \rightleftharpoons \textbf{Mn}^\textbf{3+}+e^{-}\)	\(\textbf{As(III)}(a q)+2 \text{Mn}^{3+}(aq) \rightleftharpoons \text{As(V)}(a q)+2 \text{Mn}^{2+}(a q)\)
Nota: El reactivo generado electroquímicamente y el analito se muestran en negrita.

Para un analito que no es fácil de oxidar o reducir, podemos completar una titulación culombimétrica acoplando la oxidación o reducción de un mediador a una reacción ácido-base, precipitación o complejación que involucra al analito. Por ejemplo, si usamos H ₂ O como mediador, podemos generar H ₃ O ⁺ en el ánodo

\[6 \mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons 4 \mathrm{H}_{3} \text{O}^{+}(a q)+\text{ O}_{2}(g)+4 e^{-} \nonumber\]

y generar OH ^— en el cátodo.

\[2 \mathrm{H}_{2} \mathrm{O}(l)+2 e^{-} \rightleftharpoons 2 \mathrm{OH}^{-}(a q)+\text{ H}_{2}(g) \nonumber\]

Si realizamos la oxidación o reducción de H ₂ O usando la celda generadora en la Figura 11.3.7 , entonces podemos dispensar selectivamente H ₃ O ⁺ u OH ^— en una solución que contenga el analito. La reacción resultante es idéntica a la de una valoración ácido-base. Las titulaciones coulométricas ácido-base se han utilizado para el análisis de ácidos y bases fuertes y débiles, tanto en matrices acuosas como no acuosas. El cuadro 11.3.3 resume varios ejemplos de titulaciones culombimétricas que involucran reacciones ácido-base, complejación y precipitación.

Tabla 11.3.3 . Titulaciones culométricas representativas mediante reacciones de ácido-base, complejación y precipitación

tipo de reacción	mediador	reactivo generado electroquímicamente y reacción	aplicación representativa
ácido-base	H 2 O	\(6 \mathrm{H}_{2} \mathrm{O} \rightleftharpoons 4 \textbf{H}_\mathbf{3} \textbf{O}^\mathbf{+}+\text{ O}_{2}+e^{-}\)	\(\textbf{OH}^\mathbf{-}(a q)+\text{ H}_{3} \mathrm{O}^{+}(a q) \rightleftharpoons 2 \mathrm{H}_{2} \mathrm{O}(l)\)
ácido-base	H 2 O	\(2 \mathrm{H}_{2} \mathrm{O}+2 e^{-}\rightleftharpoons 2 \textbf{OH}^\mathbf{-}+\text{ H}_{2}\)	\(\textbf{H}_\mathbf{3} \textbf{O}^\mathbf{+}(a q)+\text{ OH}^{-}(a q) \rightleftharpoons 2 \mathrm{H}_{2} \mathrm{O}(l)\)
complejación	HgNH 3 Y ^2— (Y = EDTA)	\(\mathrm{HgNH}_{3} \mathrm{Y}^{2-}+\text{ NH}_{4}^{+} + 2 e^{-} \rightleftharpoons \\ \textbf{HY}^\mathbf{3-}+\text{ Hg}+2 \mathrm{NH}_{3}\)	\(\mathbf{Ca}^\mathbf{2+}(a q)+ \text{ HY}^{3-}(a q)+ \text{ H}_{2} \text{O}(l)\rightleftharpoons \\ \text{CaY}^{2-}(a q)+ \text{ H}_{3} \text{O}^{+}(a q)\)
complejación	Ag	\(\mathrm{Ag} \rightleftharpoons \textbf{ Ag}^\mathbf{+}+e^{-}\)	\(\mathbf{I}^\mathbf{-}(a q)+\text{ Ag}^{+}(a q) \rightleftharpoons \operatorname{Ag} \mathrm{I}(s)\)
precipitación	Hg	\(2 \mathrm{Hg} \rightleftharpoons \mathbf{H} \mathbf{g}_{2}^{2+}+2 e^{-}\)	\(2 \textbf{Cl}^\mathbf{-}(a q)+\text{ Hg}_{2}^{2+}(a q) \rightleftharpoons \text{ Hg}_{2} \mathrm{Cl}_{2}(s)\)
precipitación	\(\text{Fe(CN)}_6^{3-}\)	\(\mathrm{Fe}(\mathrm{CN})_{6}^{3-}+e^{-}\rightleftharpoons \textbf{ Fe(CN)}_\mathbf{6}^\mathbf{4-}\)	\(3 \mathbf{Zn}^\mathbf{2+}(a q)+ \text{K}^{+}(a q) +2 \text{Fe(CN)}_{6}^{4-}(a q) \rightleftharpoons \\ \text{K}_{2} \text{Zn}_{3}\left[\text{Fe(CN)}_{6}\right]_{2}(s) \)
Nota: El reactivo generado electroquímicamente y el analito se muestran en negrita.

En comparación con una valoración convencional, una valoración culombimétrica tiene dos ventajas importantes. La primera ventaja es que generar electroquímicamente un valorante nos permite utilizar un reactivo que es inestable. Aunque no podemos preparar y almacenar una solución de un reactivo altamente reactivo, como Ag ^{2 +} o Mn ^{3 +}, podemos generarlos electroquímicamente y usarlos en una titulación coulométrica. Segundo, debido a que es relativamente fácil medir una pequeña cantidad de carga, podemos usar una titulación culombimétrica para determinar un analito cuya concentración es demasiado pequeña para una valoración convencional.

Cálculos cuantitativos

La cantidad absoluta de analito en un análisis coulométrico se determina usando la ley de Faraday (Ecuación\ ref {11.1}) y la carga total dada por la Ecuación\ ref {11.2} o por la Ecuación\ ref {11.3}. El siguiente ejemplo muestra los cálculos para un análisis coulométrico típico.

Ejemplo 11.3.1

Para determinar la pureza de una muestra de Na ₂ S ₂ O ₃, se valora culombimétricamente una muestra usando I ^—como mediador y\(\text{I}_3^-\) como valorante. Una muestra que pesa 0.1342 g se transfiere a un matraz aforado de 100 mL y se diluye a volumen con agua destilada. Se transfiere una porción de 10.00 ml a una celda electroquímica junto con 25 mL de KI 1 M, 75 mL de un tampón fosfato pH 7.0 y varias gotas de una solución indicadora de almidón. La electrólisis a una corriente constante de 36.45 mA requiere 221.8 s para alcanzar el punto final del indicador de almidón. Determinar la pureza de la muestra.

Solución

Como se muestra en la Tabla 11.3.2 , la valoración coulométrica de\(\text{S}_2 \text{O}_3^{2-}\) con\(\text{I}_3^-\) es

\[2 \mathrm{S}_{2} \mathrm{O}_{3}^{2-}(a q)+\text{ I}_{3}^{-}(a q)\rightleftharpoons \text{ S}_{4} \mathrm{O}_{6}^{2-}(a q)+3 \mathrm{I}^{-}(a q) \nonumber\]

La oxidación de\(\text{S}_2 \text{O}_3^{2-}\) a\(\text{S}_4 \text{O}_6^{2-}\) requiere un electrón por\(\text{S}_2 \text{O}_3^{2-}\) (n = 1). Combinando la Ecuación\ ref {11.1} y la Ecuación\ ref {11.2}, y resolviendo para los moles y gramos de Na ₂ S ₂ O ₃ da

\[N_{A} =\frac{i t_{e}}{n F}=\frac{(0.03645 \text{ A})(221.8 \text{ s})}{\left(\frac{1 \text{ mol } e^{-}}{\text{mol Na}_{2} \mathrm{S}_{2} \mathrm{O}_{3}}\right)\left(\frac{96487 \text{ C}}{\text{mol } e^{-}}\right)} =8.379 \times 10^{-5} \text{ mol Na}_{2} \mathrm{S}_{2} \mathrm{O}_{3} \nonumber\]

Esta es la cantidad de Na ₂ S ₂ O ₃ en una porción de 10.00-mL de una muestra de 100-mL; así, hay 0.1325 gramos de Na ₂ S ₂ O ₃ en la muestra original. La pureza de la muestra, por lo tanto, es

\[\frac{0.1325 \text{ g} \text{ Na}_{2} \mathrm{S}_{2} \mathrm{O}_{3}}{0.1342 \text{ g} \text { sample }} \times 100=98.73 \% \text{ w} / \text{w } \mathrm{Na}_{2} \mathrm{S}_{2} \mathrm{O}_{3} \nonumber\]

Tenga en cuenta que para la Ecuación\ ref {11.1} y la Ecuación\ ref {11.2} no importa si\(\text{S}_2 \text{O}_3^{2-}\) se oxida en el electrodo de trabajo o se oxida por\(\text{I}_3^-\).

Ejercicio 11.3.1

Para analizar una aleación de latón, se disuelve una muestra de 0.442 g en ácido y se diluye a volumen en un matraz aforado de 500 ml. La electrólisis de una muestra de 10.00-mL a —0.3 V versus un SCE reduce Cu ^{2 +} a Cu, requiriendo una carga total de 16.11 C. Ajustar el potencial a —0.6 V versus un SCE y completar la electrólisis requiere 0.442 C para reducir Pb ^{2 +} a Pb. Reportan el% w/w de Cu y Pb en la aleación.

Contestar

La reducción de Cu ^{2 +} a Cu requiere de dos electrones por mol de Cu (n = 2). Usando la Ecuación\ ref {11.1}, calculamos los moles y los gramos de Cu en la porción de muestra que se está analizando.

\[N_{C u}=\frac{Q}{n F}=\frac{16.11 \text{ C}}{\frac{2 \text{ mol } e^{-}}{\mathrm{mol} \text{ Cu}} \times \frac{96487 \text{ C}}{\text{ mol } e^{-}}}=8.348 \times 10^{-5} \text{ mol Cu} \nonumber\]

\[8.348 \times 10^{-5} \text{ mol Cu} \times \frac{63.55 \text{ g Cu} }{\text{mol Cu}}=5.301 \times 10^{-3} \text{ g Cu} \nonumber\]

Este es el Cu de una porción de 10.00 mL de una muestra de 500.0 mL; así, el cobre %/w/w en la muestra original de latón es

\[\frac{5.301 \times 10^{-3} \text{ g Cu} \times \frac{500.0 \text{ mL}}{10.00 \text{ mL}}}{0.442 \text{ g sample} } \times 100=60.0 \% \text{ w/w Cu} \nonumber\]

Para liderar, seguimos el mismo proceso; así

\[N_{\mathrm{Pb}}=\frac{Q}{n F}=\frac{0.422 \text{ C}}{\frac{2 \text{ mol } e^-}{\text{mol Pb}} \times \frac{96487 \text{ C}}{\text{mol } e^{-}}}=2.19 \times 10^{-6} \text{ mol Pb} \nonumber\]

\[2.19 \times 10^{-6} \text{ mol Pb}\times \frac{207.2 \text{ g Pb} }{\text{mol Cu} }=4.53 \times 10^{-4} \text{ g Pb} \nonumber\]

\[\frac{4.53 \times 10^{-4} \text{ g Pb} \times \frac{500.0 \text{ mL}}{10.00 \text{ mL}}}{0.442 \text{ g sample}} \times 100=5.12 \% \text{ w/w Pb} \nonumber\]

Método Representativo 11.3.1: Determinación de Dicromato mediante una Titulación Coulométrica Redox

La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método analítico típico. Aunque cada método es único, la siguiente descripción de la determinación de\(\text{Cr}_2 \text{O}_7^{2-}\) proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en Bassett, J.; Denney, R. C.; Jeffery, G. H.; Mendham, J. Vogel's Textbook of Quantitative Inorganic Analysis, Longman: London, 1978, p. 559—560.

Descripción del Método

La concentración de\(\text{Cr}_2 \text{O}_7^{2-}\) en una muestra se determina mediante una titulación redox coulométrica utilizando Fe ^{3 +} como mediador y Fe ^{3 +} electrogenerado como valorante. El punto final de la valoración se determina potenciométricamente.

Procedimiento

La celda electroquímica consiste en un electrodo de trabajo de Pt y un contraelectrodo de Pt colocados en celdas separadas conectadas por un disco de vidrio poroso. Llene la celda del contraelectrodo con 0.2 M Na ₂ SO ₄, manteniendo el nivel por encima del de la solución en la celda del electrodo de trabajo. Conecte un electrodo de platino y un electrodo de tungsteno a un potenciómetro para que pueda medir el potencial del electrodo de trabajo durante el análisis. Preparar una solución mediadora de aproximadamente 0.3 M NH ₄ Fe (SO ₄) ₂. Agregue 5.00 mL de muestra, 2 mL de 9 M H ₂ SO ₄ y 10—25 mL de la solución mediadora a la celda del electrodo de trabajo, y agregue agua destilada según sea necesario para cubrir los electrodos. Burbuja N ₂ puro a través de la solución durante 15 min para eliminar cualquier O ₂ que esté presente. Mantener el flujo de N ₂ durante la electrólisis, apagándose si se apaga momentáneamente al medir el potencial. Revuelva la solución usando una barra de agitacion magnetica. Ajustar la corriente a 15—50 mA y comenzar la titulación. Detener periódicamente la titulación y medir el potencial. Construir una curva de valoración de potencial versus tiempo y determinar el tiempo necesario para alcanzar el punto de equivalencia.

Preguntas

1. ¿El electrodo de trabajo de platino es el cátodo o el ánodo?

La reducción de Fe ^{3 +} a Fe ^{2 +} ocurre en el electrodo de trabajo, convirtiéndolo en el cátodo en esta celda electroquímica.

2. ¿Por qué es necesario eliminar el oxígeno disuelto burbujeando N ₂ a través de la solución?

Cualquier O ₂ disuelto oxidará Fe ^{2 +} de nuevo a Fe ^{3 +}, como se muestra en la siguiente reacción.

\[4\text{Fe}^{2+}(aq) + \text{ O}_2 + \text{ 4H}_3\text{O}^+(aq) \rightleftharpoons 4\text{Fe}^{3+}(aq) + 6\text{H}_2\text{O}(l) \nonumber\]

Para mantener la eficiencia de corriente, todo el Fe ^{2 +} debe reaccionar con\(\text{Cr}_2 \text{O}_7^{2-}\). La reacción de Fe ^{2 +} con O ₂ significa que se necesita más mediador Fe ^{3 +}, aumentando el tiempo para alcanzar el punto final de la titulación. En consecuencia, reportamos la presencia de demasiadas\(\text{Cr}_2 \text{O}_7^{2-}\).

3. ¿Cuál es el efecto en el análisis si el NH ₄ Fe (SO ₄) ₂ está contaminado con trazas de Fe ^{2 +}? ¿Cómo se puede compensar esta fuente de Fe ^{2 +}?

Hay dos fuentes de Fe ^{2 +}: la generada a partir del mediador y la que se presenta como impureza. Debido a que la cantidad total de Fe ^{2 +} con la que reacciona\(\text{Cr}_2 \text{O}_7^{2-}\) permanece sin cambios, se necesita menos Fe ^{2 +} del mediador. Esto disminuye el tiempo necesario para alcanzar el punto final de la titulación. Debido a que la eficiencia de corriente aparente es mayor al 100%, la concentración reportada de\(\text{Cr}_2 \text{O}_7^{2-}\) es demasiado pequeña. Podemos eliminar trazas de Fe ^{2 +} de la solución del mediador añadiendo H _{2 O 2} y calentando a 50—70 ^o C hasta que cese la evolución de O ₂, convirtiendo el Fe ^{2 +} en Fe ^{3 +}. Alternativamente, podemos completar una titulación en blanco para corregir cualquier impureza de Fe ^{2 +} en el mediador.

4. ¿Por qué el nivel de solución en la celda del contraelectrodo se mantiene por encima del nivel de solución en la celda del electrodo de trabajo?

Esto evita que la solución que contiene el analito entre en la celda del contraelectrodo. La oxidación de H ₂ O en el contraelectrodo produce O ₂, que puede reaccionar con el Fe ^{2 +} generado en el electrodo de trabajo o el Cr ^{3 +} resultante de la reacción de Fe ^{2 +} y\(\text{Cr}_2 \text{O}_7^{2-}\). En cualquier caso, el resultado es un error determinado positivo.

Aplicaciones de Caracterización

Una aplicación útil de la coulometría es determinar el número de electrones involucrados en una reacción redox. Para realizar la determinación, se realiza un análisis coulométrico de potencial controlado utilizando una cantidad conocida de un compuesto puro. La carga total al final de la electrólisis se utiliza para determinar el valor de n usando la ley de Faraday (Ecuación\ ref {11.1}).

Ejemplo 11.3.2

Una muestra de 0.3619-g de ácido tetracloropicolínico, C ₆ HNO ₂ Cl ₄, se disuelve en agua destilada, se transfiere a un matraz aforado de 1000 ml y se diluye a volumen. Una electrólisis exhaustiva de potencial controlado de una porción de 10.00 mL de esta solución en un cátodo esponjoso de plata requiere 5.374 C de carga. ¿Cuál es el valor de n para esta reacción de reducción?

Solución

La porción de 10.00 ml de muestra contiene 3.619 mg, o\(1.39 \times 10^{-5}\) mol de ácido tetracloropicolínico. Resolviendo la ecuación\ ref {11.1} para n y hacer sustituciones apropiadas da

\[n=\frac{Q}{F N_{A}}=\frac{5.374 \text{ C}}{\left(96478 \text{ C/mol } e^{-}\right)\left(1.39 \times 10^{-5} \text{ mol } \mathrm{C}_{6} \mathrm{HNO}_{2} \mathrm{Cl}_{4}\right)} = 4.01 \text{ mol e}^-/\text{mol } \mathrm{C}_{6} \mathrm{HNO}_{2} \mathrm{Cl}_{4} \nonumber\]

Así, reducir una molécula de ácido tetracloropicolínico requiere cuatro electrones. La reacción global, que resulta en la formación selectiva de ácido 3,6-dicloropicolínico, es

Evaluación

Escala de Operación

Un método coulométrico de análisis puede analizar una pequeña cantidad absoluta de un analito. En la coulometría de corriente controlada, por ejemplo, los moles de analito consumidos durante una electrólisis exhaustiva vienen dados por la Ecuación\ ref {11.11}. Una electrólisis que utiliza una corriente constante de 100 μA por 100 s, por ejemplo, consume solo\(1 \times 10^{-7}\) mol de analito si n = 1. Para un analito con un peso molecular de 100 g/mol,\(1 \times 10^{-7}\) mol de analito corresponde a solo 10 μg. La concentración de analito en la celda electroquímica, sin embargo, debe ser suficiente para permitir una determinación precisa del punto final. Cuando se usa un punto final visual, la concentración más pequeña de analito que se puede determinar mediante una titulación culombimétrica es de aproximadamente 10 ^—4 M. Como es el caso de una valoración convencional, una titulación culombimétrica usando un punto final visual se limita a analitos mayores y menores. Una valoración coulométrica a un punto final potenciométrico preestablecido es factible incluso si la concentración del analito es tan pequeña como 10 ^—7 M, extendiendo el análisis a analitos traza [Curran, D. J. “Constant-Current Coulometry”, en Kissinger, P. T.; Heineman, W. R., eds., Laboratory Techniques in Química Electroanalítica, Marcel Dekker Inc.: Nueva York, 1984, pp. 539—568].

Precisión

En la coulometría de corriente controlada, la precisión viene determinada por la precisión con la que podemos medir la corriente y el tiempo, y por la precisión con la que podemos identificar el punto final. Los errores máximos de medición para corriente y tiempo son de aproximadamente ± 0.01% y ± 0.1%, respectivamente. El error de punto final máximo para una valoración coulométrica es al menos tan bueno como el de una valoración convencional, y a menudo es mejor cuando se usan pequeñas cantidades de reactivos. En conjunto, estos errores de medición sugieren que una precisión de 0.1% — 0.3% es factible. El factor limitante en muchos análisis, por lo tanto, es la eficiencia actual. Una eficiencia de corriente superior al 99.5% es bastante rutinaria, y a menudo supera el 99.9%.

En la coulometría de potencial controlado, la precisión está determinada por la eficiencia de la corriente y por la determinación de la carga. Si la muestra está libre de interferentes que son más fáciles de oxidar o reducir que el analito, es rutinaria una eficiencia de corriente mayor al 99.9%. Cuando está presente un interferente, a menudo se puede eliminar aplicando un potencial donde la electrólisis exhaustiva de los interferentes es posible sin la electrólisis simultánea del analito. Una vez que se elimina el interferente, el potencial se cambia a un nivel donde la electrólisis del analito es factible. El factor limitante en la precisión de muchos métodos de análisis coulométricos de potencial controlado es la determinación de carga. Con los integradores electrónicos la carga total se determina con una precisión superior al 0.5%.

Si no podemos obtener una eficiencia de corriente aceptable, es posible un análisis electrogravimétrico si el analito, y solo el analito, forma un depósito sólido en el electrodo de trabajo. En este caso el electrodo de trabajo se pesa antes de comenzar la electrólisis y se vuelve a pesar cuando se completa la electrólisis. La diferencia en el peso del electrodo da la masa del analito.

Precisión

La precisión está determinada por las incertidumbres en la medición de la corriente, el tiempo y el punto final en la coulometría de corriente controlada o la carga en la culometría de potencial controlado. Precisiones de ±0.1— 0.3% se obtienen de forma rutinaria en titulaciones coulométricas, y las precisiones de ± 0.5% son típicas para la coulometría de potencial controlado.

Sensibilidad

Para un método coulométrico de análisis, la sensibilidad de calibración es equivalente a nF en la Ecuación\ ref {11.1}. En general, un método coulométrico es más sensible si la oxidación o reducción del analito implica un valor mayor de n.

Selectividad

La selectividad en la coulometría de potencial controlado y corriente controlada se mejora ajustando las condiciones de la solución y seleccionando el potencial de electrólisis. En la coulometría de potencial controlado, el potencial es fijado por el potenciostato, y en la culometría de corriente controlada el potencial está determinado por la reacción redox con el mediador. En cualquier caso, la capacidad de controlar el potencial de electrólisis proporciona alguna medida de selectividad. Ajustando el pH o añadiendo un agente complejante, es posible desplazar el potencial al que un analito o interferente sufre oxidación o reducción. Por ejemplo, el potencial de reducción de estado estándar para Zn ^{2 +} es —0.762 V versus el SHE. Si agregamos una solución de NH ₃, formando\(\text{Zn(NH}_3\text{)}_4^{2+}\), el potencial de estado estándar cambia a —1.04 V. Esto proporciona un medio adicional para controlar la selectividad cuando un analito y un interferente experimentan electrólisis a potenciales similares.

Tiempo, Costo y Equipo

La culometría de potencial controlado es un análisis que consume relativamente tiempo, con un análisis típico que requiere de 30 a 60 min. Las titulaciones coulométricas, por otro lado, requieren solo unos minutos, y son fáciles de adaptar a un análisis automatizado. La instrumentación comercial para la coulometría tanto de potencial controlado como de corriente controlada está disponible, y es relativamente económica. Potenciostatos de bajo costo y fuentes de corriente constante están disponibles por aproximadamente $1000.