8.3: Análisis de las Gráficas de Funciones
- Page ID
- 106020
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dado un conjunto de información sobre las propiedades clave de una función, puede bosquejar la gráfica. Antes de continuar, haz un intento de resumir para lo que crees que son propiedades clave. A menudo, las propiedades clave de una función no se le presentan todas directamente, sino que deben determinarse a partir de la información que tenga a mano.
Análisis de Gráficas de Funciones
Primero resumiremos el tipo de información sobre funciones que ahora podemos generar en base a nuestros conceptos anteriores. Luego utilizaremos esta información para analizar ejemplos de funciones representativas racionales, polinomiales, radicales y trigonométricas.
Usemos una tabla como la que se muestra como plantilla para organizar nuestros hallazgos.
| f (x) = | Análisis |
| Dominio y Rango | |
| Intercepciones y ceros | |
| Asíntotas y límites al infinito | |
| Diferenciabilidad | |
| Intervalos donde f está aumentando | |
| Intervalos donde f es decreciente | |
| Extremos relativos | |
| Concavidad | |
| Puntos de inflexión |
Análisis de funciones racionales
Considerar la función racional\( f(x)=\frac{x^2−4}{x^2−2x−8} \nonumber\).
Ceros, dominio y rango
La función parece tener ceros en x=±2. Sin embargo, una vez factorizamos la expresión vemos
\( \frac{x^2−4}{x^2−2x−8}=\frac{(x+2)(x−2)}{(x−4)(x+2)}= \frac{x−2}{x−4} \nonumber\)
Por lo tanto, la función tiene un cero en x=2, hay un agujero en la gráfica en x=−2, el dominio es\( (−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\), y la intercepción y está en (0,12).
Asíntotas y límites en el infinito
Dado el dominio, observamos que hay una asíntota vertical en x=4. Para determinar otras asíntotas, examinamos el límite de f como x→∞ y x→−∞. Tenemos
\[ \lim_{x \to ∞} \frac{x^2−4}{x^2−2x−8}= \lim_{x \to ∞} \frac{ \frac{x^2}{x^2}−\frac{4}{x^2}} {\frac{x^2}{x^2}−\frac{2x}{x^2}−\frac{8}{x^2}}=\lim_{x \to ∞} \frac{1−\frac{4}{x^2}}{1−\frac{2}{x}−\frac{8}{x^2}}=1 \nonumber\].
De igual manera, eso lo vemos\( \lim_{x \to −∞} \frac{x^2−4}{x^2−2x−8}=1 \nonumber\). También observamos que\( y≠\frac{2}{3} \nonumber\) desde x≠ −2.
De ahí que tengamos una asíntota horizontal en y=1.
Diferenciabilidad
\( f′(x)=\frac{−2x^2−8x−8}{(x2−2x−8)}=\frac{−2}{(x−4)^2}<0 \nonumber\). De ahí que la función sea diferenciable en cada punto de su dominio, y dado que f′ (x) <0 en su dominio, entonces f está disminuyendo en su dominio,\( (−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\).
\[ f′′(x)= \frac{4}{(x−4)^3} \nonumber\].
f′′ (x) ≠ 0 en el dominio de f. De ahí que no haya extremos relativos ni puntos de inflexión.
De manera similar, f′′ (x) <0 cuando x<4. Por lo tanto, la gráfica es cóncava hacia abajo para x<4, x≠ −2.
Resumimos nuestros resultados en la tabla antes de bosquejar la gráfica.
| f (x) =x2−4x2−2x−8 | Análisis |
| Dominio y Rango |
\( D=(−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\) \ (R= {\ mbox {todos los reales} ≠ 1o\ frac {2} {3}} |
| Intercepciones y ceros |
Cero a x=2, y− interceptar en (0,\( \frac{1}{2} \nonumber\)) |
| Asíntotas y límites al infinito |
VA a x=4, HA en y=1, Agujero en la gráfica en x=−2 |
| Diferenciabilidad | Diferenciable en cada punto de su dominio |
| Intervalos donde f está aumentando | En ninguna parte |
| Intervalos donde f es decreciente | \( (−∞,−2)∪(−2,4)∪(4,+∞) \nonumber\) |
| Extremos relativos | Ninguno |
| Concavidad |
Cóncavo hacia arriba en (4, +∞), Cóncavo hacia abajo\( (−∞,−2)∪(−2,4) \nonumber\) |
| Puntos de inflexión |
Ninguno |
Finalmente, esbozamos la gráfica de la siguiente manera:
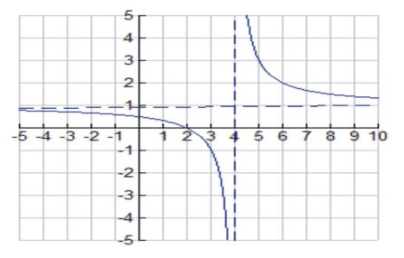
CC BY-NC-SA
Análisis de funciones radicales
Ahora, considere la función\( f(x)= \sqrt{2x−1} \nonumber\).
Ceros, dominio y rango
El dominio de f es\( (\frac{1}{2},+∞) \nonumber\), y tiene un cero at\(x=\frac{1}{2} \nonumber\).
Asíntotas y límites en el infinito
Dado el dominio, observamos que no hay asíntotas verticales. Tomamos nota de eso\( \lim_{x \to ∞} f(x)=+∞ \nonumber\).
Diferenciabilidad
\( f′(x)=\frac{1}{\sqrt{2x−1}}>0 \nonumber\)para todo el dominio de f. De ahí que f esté aumentando en todas partes en su dominio. f′ (x) no se define en\( x=\frac{1}{2} \nonumber\), por lo que\( x=\frac{1}{2} \nonumber\) es un valor crítico.
\( f′′(x)=\frac{−1}{\sqrt{(2x−1)^3}<0 \nonumber\)por todas partes en\( (\frac{1}{2},+∞) \nonumber\). De ahí que f sea cóncava hacia abajo en\( (\frac{1}{2},+∞) \nonumber\).
f′ (x) no se define en\( x=\frac{1}{2} \nonumber\), por lo que\( x=\frac{1}{2} \nonumber\) es un mínimo absoluto.
| f (x) =2x√−1 | Análisis |
| Dominio y Rango |
\( D=(\frac{1}{2},+∞),R={y≥0} \nonumber\) |
| Intercepciones y ceros |
Cero en\( x=\frac{1}{2} \nonumber\), No hay intercepción y− |
| Asíntotas y límites al infinito |
Sin asíntotas |
| Diferenciabilidad | Diferenciable en (\( \frac{1}{2} \nonumber\), +∞) |
| Intervalos donde f está aumentando | En todas partes en D= (\( \frac{1}{2} \nonumber\), +∞) |
| Intervalos donde f es decreciente | En ninguna parte |
| Extremos relativos | Ninguno |
| Concavidad |
Mínimo absoluto en x=\( \frac{1}{2} \nonumber\), ubicado en (\( \frac{1}{2} \nonumber\),0) Cóncavo hacia abajo en (\( \frac{1}{2} \nonumber\), +∞) |
| Puntos de inflexión |
Ninguno |
Aquí hay un boceto de la gráfica:
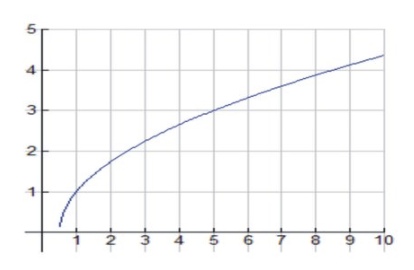
CC BY-NC-SA
Análisis de funciones trigonométricas
Veremos que si bien las funciones trigonométricas se pueden analizar utilizando lo que sabemos sobre los derivados, brindarán algunos desafíos interesantes que necesitaremos abordar.
Considera la función\( f(x)=x−2sinx \nonumber\) en el intervalo\( [−π,π] \nonumber\).
Ceros, dominio y rango
Observamos que f es una función continua y alcanza un máximo absoluto y mínimo en\( [−π,π] \nonumber\). Su dominio es\( [−π,π] \nonumber\), y su rango es\( R={−π≤y≤π} \nonumber\).
Diferenciabilidad
\[ f′(x)=1−2cosx=0 \mbox{ at } x=−\frac{π}{3},\frac{π}{3} \nonumber\].
Tenga en cuenta que\( f′(x)>0 \mbox{ on } (−π,−\frac{π}{3}) \mbox{ and } (\frac{π}{3},π) \nonumber\); por lo tanto, la función está aumentando en (−π, −π3) y (π3, π).
Tenga en cuenta que f′ (x) <0 on (−π3, π3); por lo tanto, la función está disminuyendo en (−π3, π3).
f′′ (x) =2sinx=0 si x=0, π, −π. Por lo tanto, los valores críticos están en x=−π, −π3, π3 y π.
f′′ (π3) >0; por lo tanto, hay un mínimo relativo en x=π3.
f′′ (−π3) <0; por lo tanto, hay un máximo relativo en x=−π3.
f′′ (x ≈0 <0 on (−π,0) and f′′ (x) > on (0, π). De ahí que la gráfica sea cóncava hacia abajo en (−π,0) y cóncava hacia arriba y decreciente en (0, π). Hay un punto de inflexión en x=0, ubicado en el punto (0, 0).
Finalmente, hay mínimo absoluto en\( x=−π \nonumber\), ubicado en\( (−π,−π) \nonumber\), y un máximo absoluto en\( x=π \nonumber\), ubicado en\( (π,π) \nonumber\).
| f (x) =x−2sinx | Análisis |
| Dominio y Rango |
\( D=[−π,π],R={−π≤y≤π} \nonumber\) |
| Intercepciones y ceros |
\( x=−\frac{π}{3}, \frac{π}{3} \nonumber\) |
| Asíntotas y límites al infinito |
Sin asíntotas |
| Diferenciabilidad | Diferenciable en\( D=[−π,π] \nonumber\) |
| Intervalos donde f está aumentando | \( (\frac{π}{3},π) \mbox{ and } (−π,−\frac{π}{3}) \nonumber\) |
| Intervalos donde f es decreciente | \ ((−\ frac {π} {3},\ frac {π} {3}) |
| Extremos relativos |
Máximo relativo en\( x=−\frac{π}{3} \nonumber\) Mínimo relativo en\( x=\frac{π}{3} \nonumber\) |
| Concavidad |
Máximo absoluto en x=π, localizado en (π, π) Mínimo absoluto en x=−π, ubicado en (−π, −π) Cóncavo hacia arriba en (0, π) |
| Puntos de inflexión |
x=0, ubicado en el punto (0, 0) |
Aquí hay un boceto de la gráfica:
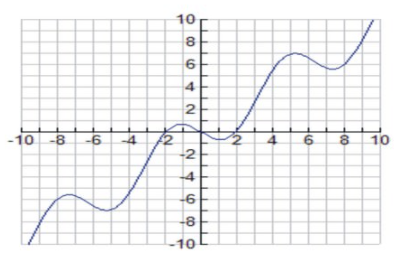
CC BY-NC-SA
Ejemplos
Ejemplo 1
Anteriormente, se le pidió que resumiera las propiedades clave de las funciones. Como has visto en este concepto, las propiedades clave de las funciones incluyen: dominio, rango, intercepciones, asíntotas (incluyendo límites al infinito), continuidad y diferenciabilidad, intervalos crecientes y decrecientes, extremos, concavidad y puntos de inflexión.
Ejemplo 2
Considerar la función polinómica\(f(x)=x^3+2x^2−x−2 \nonumber\).
Ceros, dominio y rango
El dominio de f es (−∞, +∞) y la intercepción y en (0, -2).
La función puede ser factorizada\( f(x)=x^3+2x^2−x−2=x^2(x+2)−1(x+2)=(x^2−1)(x+2)=(x−1)(x+1)(x+2) \nonumber\)
y por lo tanto tiene ceros en x=±1, −2.
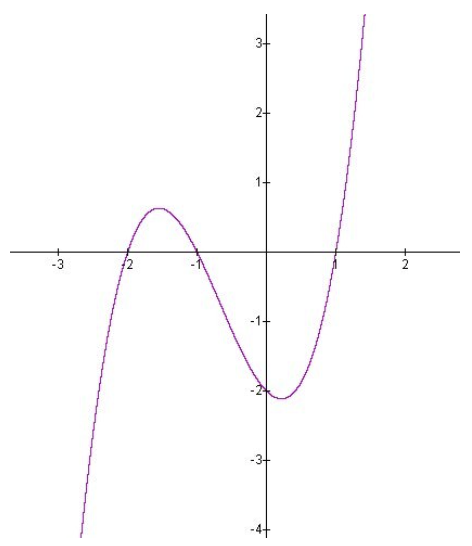
CC BY-NC-SA
Asíntotas y límites al infinito
Dado el dominio, observamos que no hay asíntotas verticales. Tomamos nota de que y\( \lim_{x \to ∞} f(x)=+∞ \mbox{ and } \lim_{x \to {−∞}} f(x)=−∞ \nonumber\).
Diferenciabilidad
\( f′(x)=3x^2+4x−1=0 \mbox{ if } x=\frac{−4±\sqrt{28}}{6}=\frac{−2±\sqrt{7}}{3} \nonumber\). Estos son los valores críticos. Observamos que la función es diferenciable en cada punto de su dominio.
\( f′(x)>0 \mbox{ on } (−∞,\sqrt{−2−\sqrt{7}}{3}) \mbox{ and } (\frac{−2+\sqrt{7}}{3},+∞) \nonumber\); de ahí que la función esté aumentando en estos intervalos.
Del mismo modo,\( f′(x)<0 \mbox{ on } (\frac{−2−\sqrt{7}}{3},\fraac{−2+\sqrt{7}}{3}) \nonumber\) y así es f decreciente ahí.
\( f′′(x)=6x+4=0 \mbox{ if } x=−\frac{2}{3} \nonumber\)donde hay un punto de inflexión.
Además,\( f′′(\frac{−2−\sqrt{7}}{3})<0 \nonumber\). De ahí que la gráfica tenga un máximo relativo en\( x=\frac{−2−\sqrt{7}}{3} \nonumber\) y localizado en el punto (-1.55, 0.63).
Tomamos nota de eso\( f′′(x)<0 \mbox{ for } x<−\sqrt{2}{3} \nonumber\). La gráfica es cóncava hacia abajo en\( (−∞,−\frac{2}{3}) \nonumber\).
Y tenemos\( f′′(\frac{−2+\sqrt{7}}{3})>0 \nonumber\); de ahí que la gráfica tenga un mínimo relativo en\( x=\frac{−2+\sqrt{7}}{3} \nonumber\) y localizado en el punto (0.22, -2.11).
Tomamos nota de eso\( f′′(x)>0 \mbox{ for } x>−\frac{2}{3} \nonumber\). La gráfica es cóncava hacia arriba en\( (−\frac{2}{3},+∞) \nonumber\).
Resumen de la tabla
| \( f(x)=x^3+2x^2−x−2 \nonumber\) | Análisis |
| Dominio y Rango |
D= (−∞, +∞), R= {todos los reales} |
| Intercepciones y ceros |
Ceros en x=±1, −2, y, intercepta en (0, -2) |
| Asíntotas y límites al infinito |
Sin asíntotas |
| Diferenciabilidad | Diferenciable en cada punto de su dominio |
| Intervalos donde f está aumentando | \( (−∞,\frac{−2−\sqrt{7}}{3}) and (\frac{−2+\frac{7}}{3},+∞) \nonumber\) |
| Intervalos donde f es decreciente | \( (\frac{−2−\sqrt{7}}{3},\frac{−2+\sqrt{7}}{3}) \nonumber\) |
| Extremos relativos |
Máximo relativo en\( x=\frac{−2−\sqrt{7}}{3} \nonumber\) y localizado en el punto (-1.55, 0.63); Mínimo relativo en\( x=\frac{−2+\sqrt{7}}{3} \nonumber\) y localizado en el punto (0.22, -2.11). |
| Concavidad |
Cóncava hacia arriba en\( (−\frac{2}{3},+∞) \nonumber\). Cóncava hacia abajo en\( (−∞,−\frac{2}{3}) \nonumber\). |
| Puntos de inflexión |
\( x=−\frac{2}{3} \nonumber\), ubicado en el punto\( (−\frac{2}{3},−.74) \nonumber\) |
Aquí hay un boceto de la gráfica:
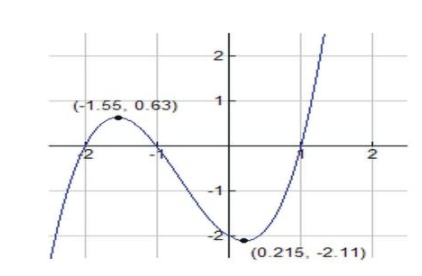
CC BY-NC-SA
Revisar
Para todas las siguientes funciones, resuma las funciones rellenando la siguiente tabla. Utilice la información para esbozar una gráfica de la función.
| f (x) = | Análisis |
| Dominio y Rango | |
| Intercepciones y ceros | |
| Asíntotas y límites al infinito | |
| Diferenciabilidad | |
| Intervalos donde f está aumentando | |
| Intervalos donde f es decreciente | |
| Extremos relativos | |
| Concavidad | |
| Puntos de inflexión |
- \( f(x)=x^3+3x^2−x−3 \nonumber\)
- \( f(x)=−x^4+4x^3−4x^2 \nonumber\)
- \( f(x)=\frac{2x−2}{x^2} \nonumber\)
- \( f(x)=x−x^{\frac{1}{3}} \nonumber\)
- \( f(x)=−\sqrt{2x−6}+3 \nonumber\)
- \( f(x)=x^2−2\sqrt{x} \nonumber\)
- \( f(x)=1+cosx \mbox{ on the interval } [−π,π] \nonumber\)
- \( f(x)=x^2−x+1 \nonumber\)
- \( f(x)=4x^3−6x^2−1 \nonumber\)
- \( f(x)=\frac{x^2}{x−1} \nonumber\)
- \( f(x)=\frac{x^2}{e^{−x}} \nonumber\)
- \( f(x)=cosx−x \nonumber\)
- \( f(x)=e^{−2x}+e^x \nonumber\)
- \( f(x)=5e^{−x}+x^3 \nonumber\)
- \( f(x)=x^5−7x^2+2 \nonumber\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.8.
vocabulario
| Término | Definición |
|---|---|
| Asíntotas | Una asíntota es una línea en la gráfica de una función que representa un valor hacia el que la función puede acercarse, pero no alcanza (con ciertas excepciones). |
| concavidad | La concavidad describe el comportamiento de la pendiente de la línea tangente de una función de tal manera que la concavidad es positiva si la pendiente está aumentando, negativa si la pendiente es decreciente, y cero si la pendiente es constante. |
| decreciente | Una función disminuye a lo largo de un intervalo si sus valores y son cada vez más pequeños a lo largo del intervalo. El gráfico bajará de izquierda a derecha a lo largo del intervalo. |
| diferenciable | Una función diferenciable es una función que tiene una derivada que se puede calcular. |
| dominio | El dominio de una función es el conjunto de valores x para los que se define la función. |
| aumentando | Una función aumenta a lo largo de un intervalo si sus valores y son cada vez mayores a lo largo del intervalo. La gráfica irá hacia arriba de izquierda a derecha a lo largo del intervalo. |
| punto de inflexión | Un punto de inflexión es un punto en el dominio donde la concavidad cambia de positiva a negativa o negativa a positiva. |
| Rango | El rango de una función es el conjunto de valores y para los que se define la función. |
| extremos relativos | Los extremos relativos de una función son los puntos de la función con valores y que son los más altos o más bajos de un vecindario local de la función. |
Recursos adicionales
PLIX: Juega, aprende, interactúa, explora - Analizando una función racional
Vídeo: Graficar usando Derivados
Mundo real: Eliminación total

