4.4: Triángulos isósceles
- Page ID
- 107555
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Propiedades de triángulos con dos lados/ángulos iguales.
Un triángulo isósceles es un triángulo que tiene al menos dos lados congruentes. Los lados congruentes del triángulo isósceles se llaman patas. Al otro lado se le llama la base. Los ángulos entre la base y las patas se denominan ángulos de base. El ángulo formado por las dos patas se denomina ángulo de vértice. Una de las propiedades importantes de los triángulos isósceles es que sus ángulos de base son siempre congruentes. Esto se llama Teorema de Ángulos Base.
Para\(\DeltaDEF, if \(\overline{DE}\cong \overline{EF}\), entonces\(\angle D\cong \angle F\).
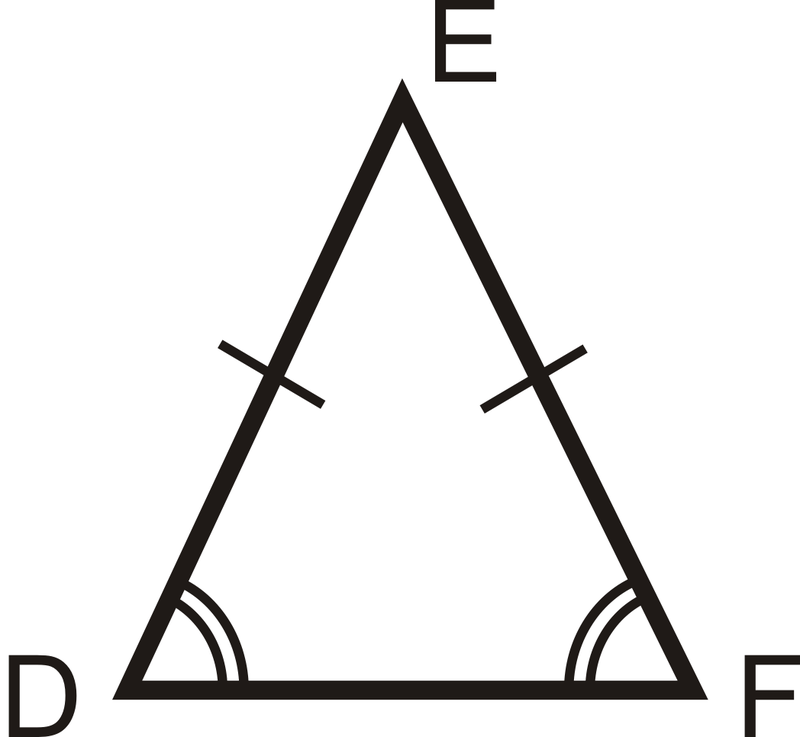
Otra propiedad importante de los triángulos isósceles es que el ángulo bisectriz del ángulo del vértice es también la bisectriz perpendicular de la base. A esto se le llama Teorema del Triángulo Isósceles. (Tenga en cuenta que esto SOLO es cierto para el ángulo del vértice. ) Las conversas del Teorema de los Ángulos Base y del Teorema del Triángulo Isósceles también son verdaderas.
Teorema de ángulos base Converse: Si dos ángulos en un triángulo son congruentes, entonces los lados opuestos a esos ángulos también son congruentes. Entonces para\(\Delta DEF\), si\(\angle D\cong \angle F\), entonces\(\overline{DE}\cong \overline{EF}\).

Teorema del Triángulo Isósceles Converse: La bisectriz perpendicular de la base de un triángulo isósceles es también el ángulo bisectriz del ángulo del vértice. Entonces para isósceles\(\DeltaDEF\), si\(\overline{EG}\perp \overline{DF}\) y\(\overline{DG}\cong \overline{GF}\), entonces\(\angle DEG\cong \angle FEG\).
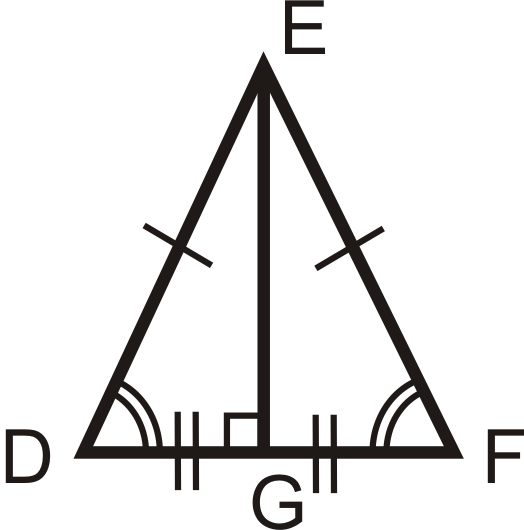
¿Y si te presentaran un triángulo isósceles y te dijeran que sus ángulos de base miden\(x^{\circ}\) y\(y^{\circ}\)? ¿De qué podrías concluir\( x\) y\(y\)?
Ejemplo\(\PageIndex{1}\)
Encuentra el valor de\( x\) y la medida de cada ángulo.
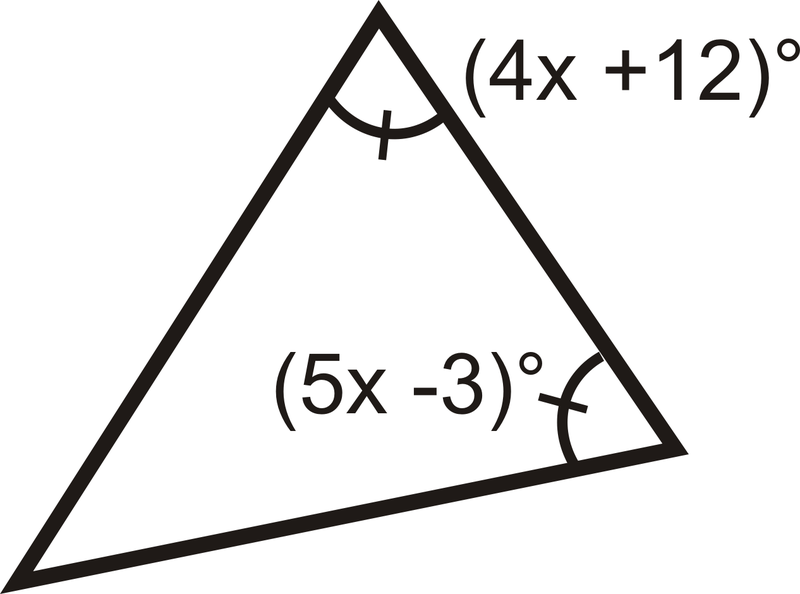
Solución
Los dos ángulos son iguales, así que ponlos iguales entre sí y resuelven para\(x\).
\(\begin{align*} (4x+12)^{\circ}&=(5x−3)^{\circ} \\ 15&=x\end{align*} \)
Sustituye x=15; los ángulos base son\([4(15)+12]^{\circ}\), o 72^ {\ circ}\). El ángulo del vértice es\(180^{\circ}−72^{\circ}−72^{\circ}=36^{\circ}\).
Ejemplo\(\PageIndex{2}\)
Verdadero o falso: Los ángulos base de un triángulo isósceles pueden ser ángulos rectos.
Solución
Esta afirmación es falsa. Debido a que los ángulos base de un triángulo isósceles son congruentes, si un ángulo base es un ángulo recto entonces ambos ángulos base deben ser ángulos rectos. Es imposible tener un triángulo con dos ángulos rectos (\(90^{\circ}\)). El Teorema de la Suma del Triángulo establece que la suma de los tres ángulos en un triángulo es\(180^{\circ}\). Si dos de los ángulos en un triángulo son ángulos rectos, entonces el tercer ángulo debe ser\(0^{\circ}\) y la forma ya no es un triángulo.
Ejemplo\(\PageIndex{3}\)
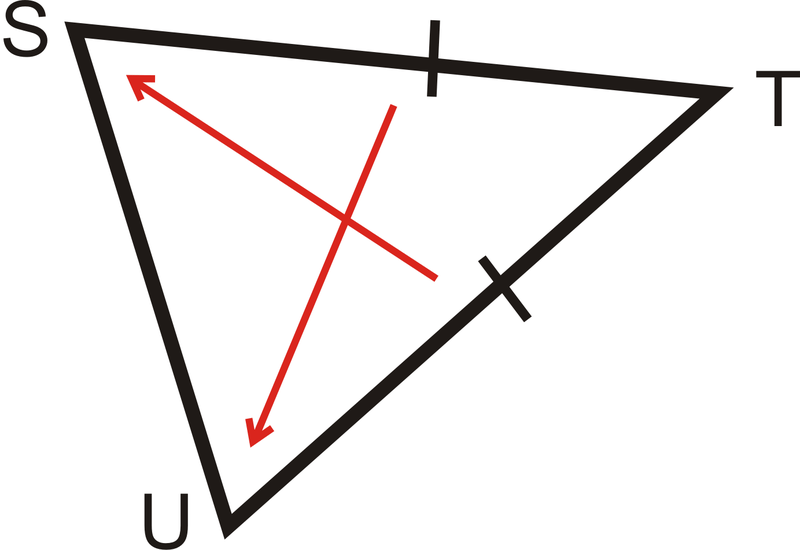
¿Cuáles dos ángulos son congruentes?
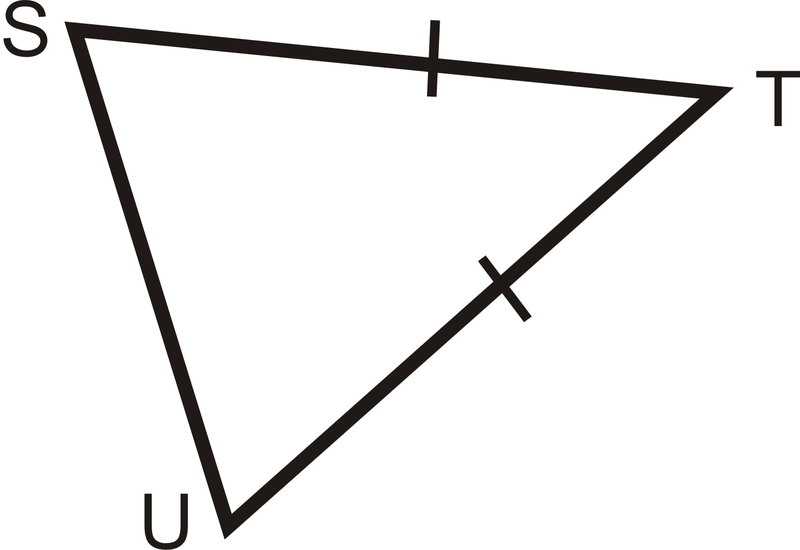
Solución
Se trata de un triángulo isósceles. Los ángulos congruentes son opuestos a los lados congruentes. De las flechas vemos eso\(\angle S\cong \angle U\).
Ejemplo\(\PageIndex{4}\)
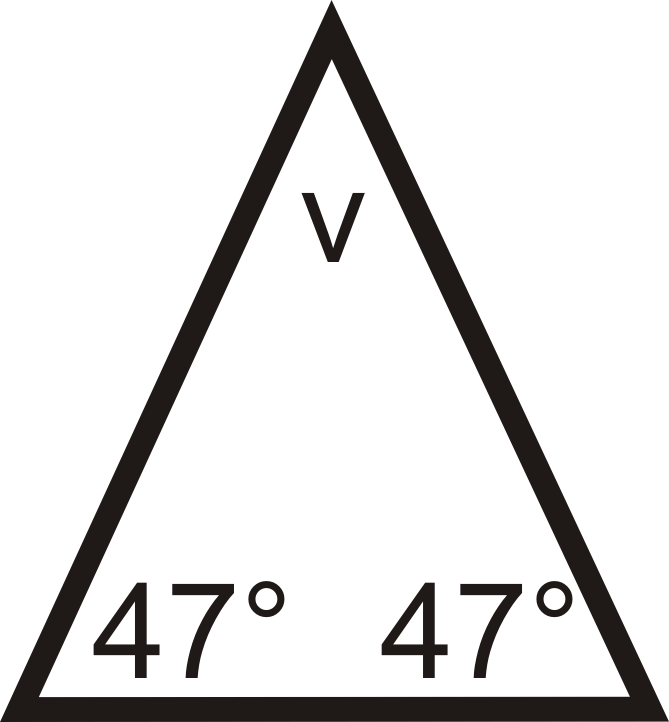
Si un triángulo isósceles tiene ángulos base con medidas de\(47^{\circ}\), ¿cuál es la medida del ángulo de vértice?
Solución
Dibuja una imagen y configura una ecuación para resolver el ángulo del vértice,\(v\). Recuerda que los tres ángulos en un triángulo siempre suman\(180^{\circ}\).
\(\begin{align*} 47^{\circ}+47^{\circ}+v &=180^{\circ} \\ v &=180^{\circ}−47^{\circ}−47^{\circ} \\ v =86^{\circ} \end{align}\)
Ejemplo\(\PageIndex{5}\)
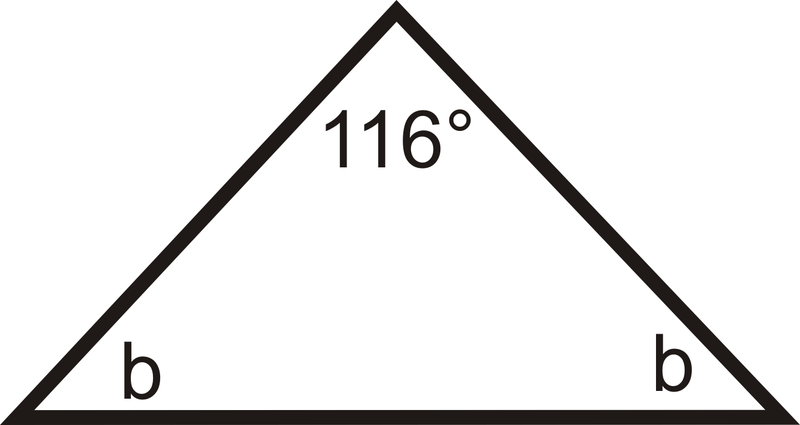
Si un triángulo isósceles tiene un ángulo de vértice con una medida de\(116^{\circ}\), ¿cuál es la medida de cada ángulo base?
Solución
Dibujar una imagen y configurar y ecuación para resolver para los ángulos de base,\(b\).
\(\begin{align*} 116^{\circ}+b+b&=180^{\circ} \\ 2b&=64^{\circ} \\ b &=32^{\circ}\end{align*}\)
Revisar
Encuentra las medidas de\( x\) y/o\(y\).
-
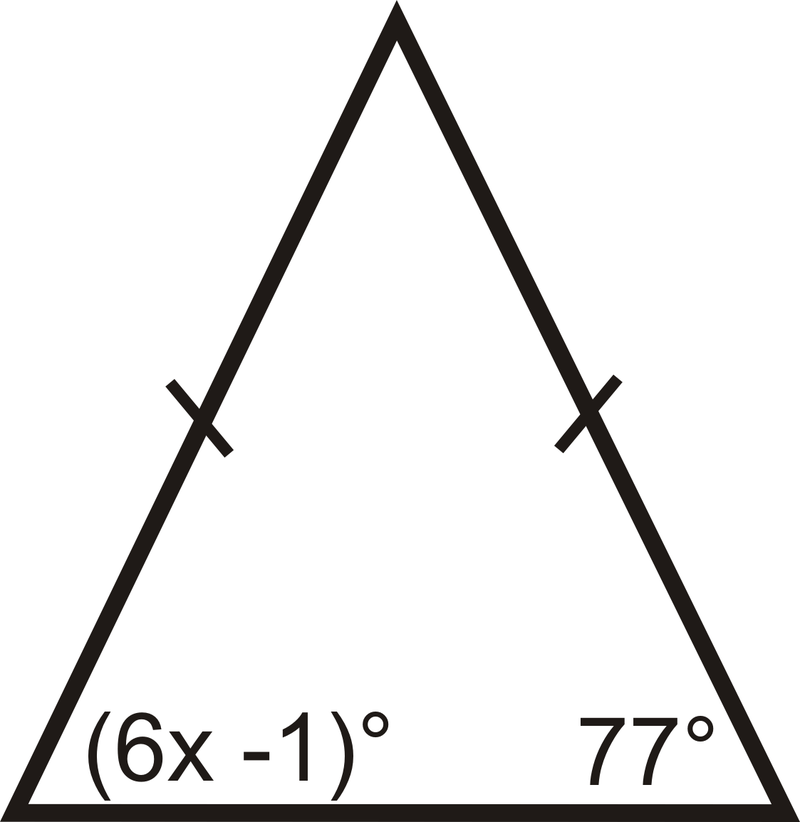
Figura\(\PageIndex{9}\) -
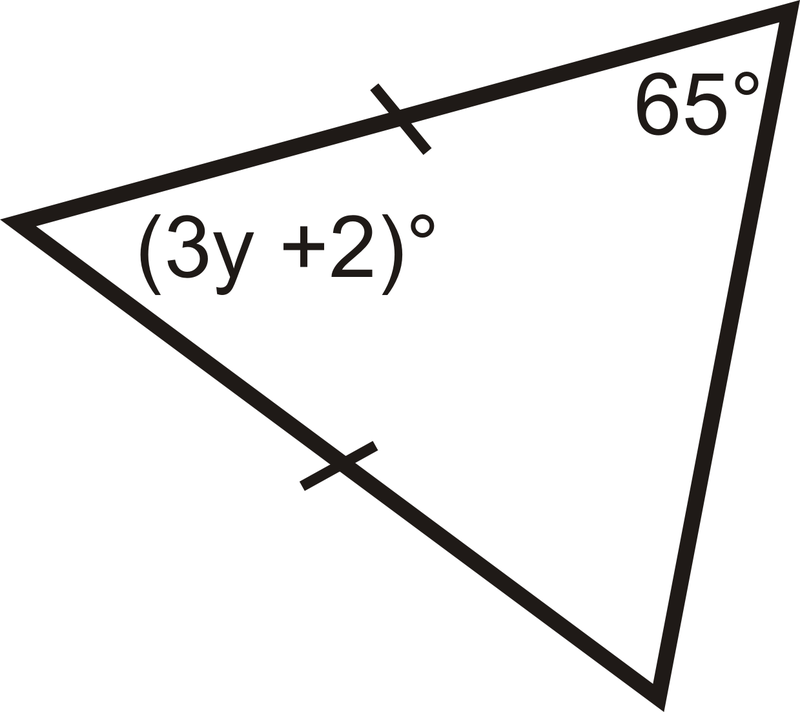
Figura\(\PageIndex{10}\) -

Figura\(\PageIndex{11}\) -
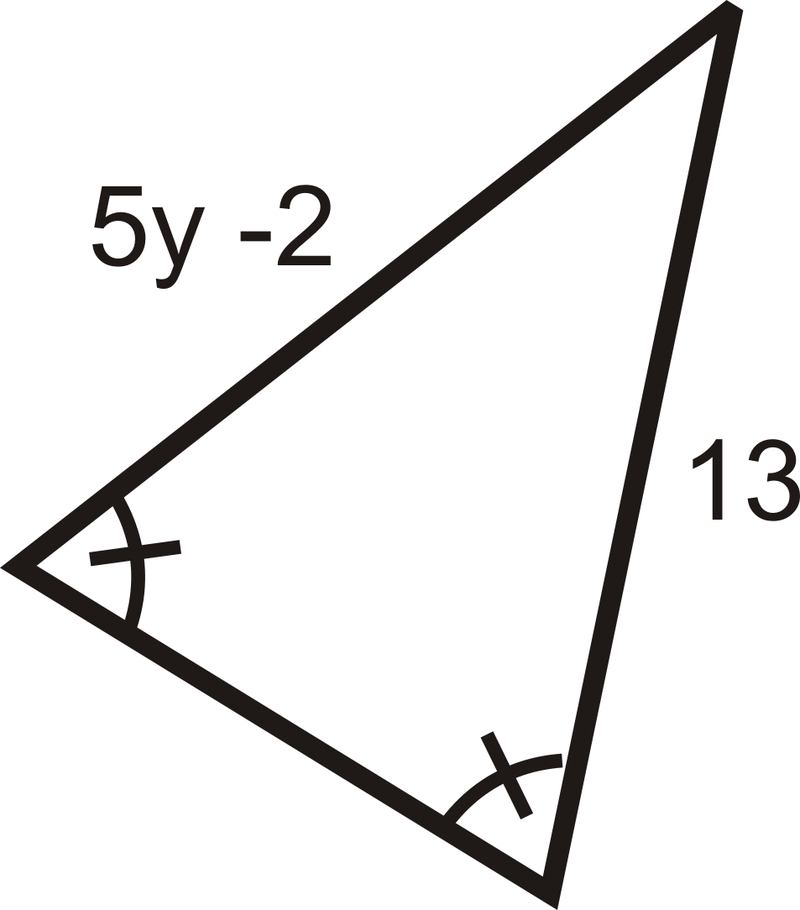
Figura\(\PageIndex{12}\) -
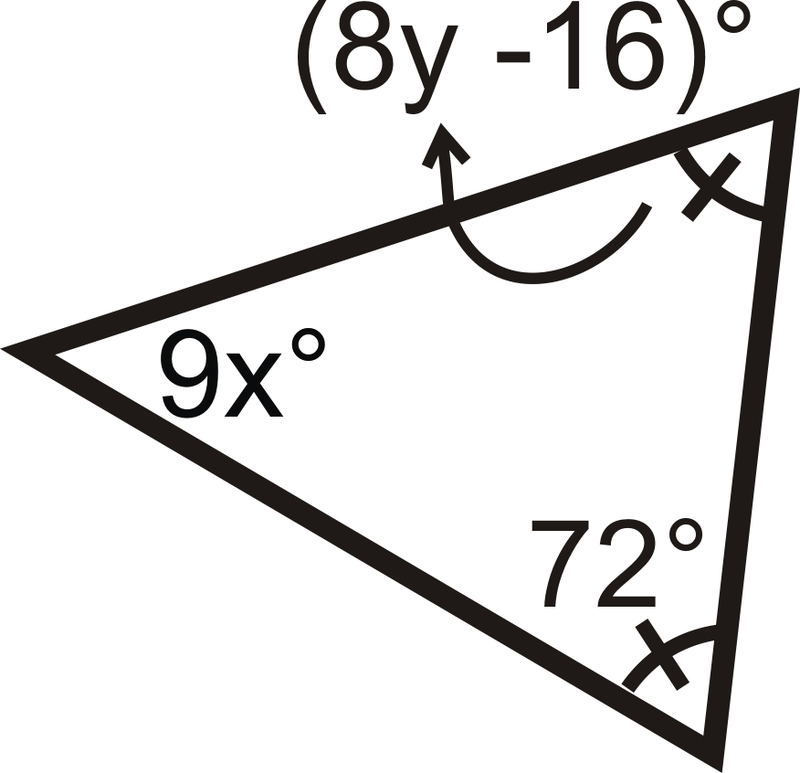
Figura\(\PageIndex{13}\)
Determinar si las siguientes afirmaciones son verdaderas o falsas.
- Los ángulos base de un triángulo isósceles son congruentes.
- Los ángulos base de un triángulo isósceles son complementarios.
- Los ángulos base de un triángulo isósceles pueden ser iguales al ángulo del vértice.
- Los ángulos de base de un triángulo isósceles son agudos.
Rellena las pruebas que aparecen a continuación.
- Dado: Isósceles\(\DeltaCIS\), con ángulos de base\(\angle C\) y\(\angle S\). \ overline {IO}\) es el ángulo bisectriz de\(\angle CIS\) Prove:\(\overline{IO}\) es la bisectriz perpendicular de\(\overline{CS}\)
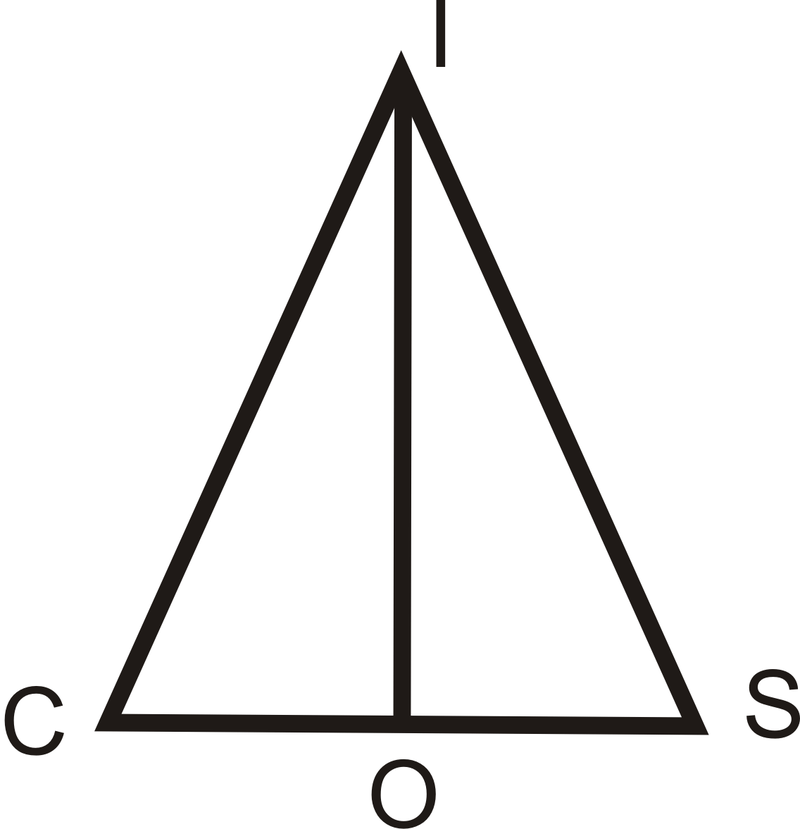
| Declaración | Razón |
|---|---|
| 1. | 1. Dado |
| 2. | 2. Teorema de ángulos de base |
| 3. \(\angle CIO\cong \angle SIO\) | 3. |
| 4. | 4. reflexivo\(PoC\) |
| 5. \(\DeltaCIO\cong \DeltaSIO\) | 5. |
| 6. \(\overline{CO}\cong \overline{OS}\) | 6. |
| 7. | 7. \(CPCTC\) |
| 8. \(\angle IOC\)y\(\angle IOS\) son complementarios | 8. |
| 9. | 9. Teorema de Suplementos Congruentes |
| 10. \(\overline{IO}\)es la bisectriz perpendicular de\(\overline{CS}\) | 10. |
- Dado: Isósceles\(\DeltaICS\) con\(\angle C\) y\(\angle S\). \(\overline{IO}\)es la bisectriz perpendicular de\(\overline{CS}\) Prove:\(\overline{IO}\) es el ángulo bisectriz de\(\angle CIS\)

| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. \(\angle C\cong \angle S\) | 2. |
| 3. \(CO\overline{AB}\cong OS\overline{AB}\) | 3. |
| 4. \(m\angle IOC=m\angle IOS=90^{\circ}\) | 4. |
| 5. | 5. |
| 6. | 6. \(CPCTC\) |
| 7. \(\overline{IO}\)es el ángulo bisectriz de\(\angle CIS\) | 7. |
En el plano x−y, traza las coordenadas y determina si los tres puntos dados forman un triángulo escaleno o isósceles.
- \((-2, 1), (1, -2), (-5, -2)\)
- \((-2, 5), (2, 4), (0, -1)\)
- \((6, 9), (12, 3), (3, -6)\)
- \((-10, -5), (-8, 5), (2, 3)\)
- \((-1, 2), (7, 2), (3, 9)\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.10.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Base | El lado de un triángulo paralelo al borde inferior del papel o pantalla se llama comúnmente la base. La base de un triángulo isósceles es el lado no congruente en el triángulo. |
| Ángulos de Base | Los ángulos de base de un triángulo isósceles son los ángulos formados por la base y una pata del triángulo. |
| Teorema de ángulos base Converse | El teorema de los ángulos base converse establece si dos ángulos en un triángulo son congruentes, entonces los lados opuestos a esos ángulos también son congruentes. |
| Teorema del Triángulo Isósceles | El Teorema del Triángulo Isósceles establece que la bisectriz perpendicular de la base de un triángulo isósceles es también el ángulo bisectriz del ángulo del vértice. |
| Teorema de suma de triángulo | El Teorema de la Suma del Triángulo establece que los tres ángulos interiores de cualquier triángulo suman 180 grados. |
| Ángulos Verticales | Los ángulos verticales son un par de ángulos opuestos creados por líneas que se cruzan. |
Recursos adicionales
Elemento Interactivo
Video: Principios de los triángulos isósceles - Básico
Actividades: Triángulos isósceles Preguntas de discusión
Ayudas de estudio: Guía de estudio de las relaciones
Práctica: Triángulos isósceles
Mundo real: Triángulos en el cielo

