4.5: Triángulos equiláteros
- Page ID
- 107533
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Propiedades de triángulos con tres lados iguales.
Teorema del Triángulo Equilátero: Todos los triángulos equiláteros también son equiangulares. Además, todos los triángulos equiangulares también son equiláteros.
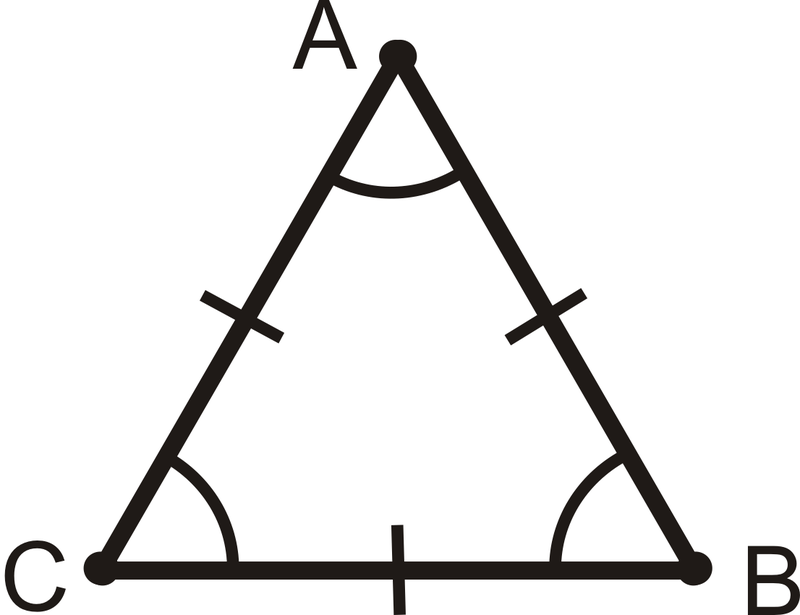
Si\(\overline{AB}\cong \overline{BC}\cong \overline{AC}\), entonces\(\angle A\cong \angle B\cong \angle C\). Por el contrario, si\(\angle A\cong \angle B\cong \angle C\), entonces\(\overline{AB}\cong \overline{BC}\cong \overline{AC}\).
¿Y si te presentaran un triángulo equilátero y te dijeran que sus lados miden\(x\), \(y\), y 8? ¿De qué podrías concluir\(x\) y\(y\)?
Ejemplo\(\PageIndex{1}\)
Rellene el comprobante:
Dado: Equilátero\(\Delta RST\) con
\(\overline{RT}\cong \overline{ST}\cong \overline{RS}\)
Demostrar:\(\Delta RST\) es equiangular
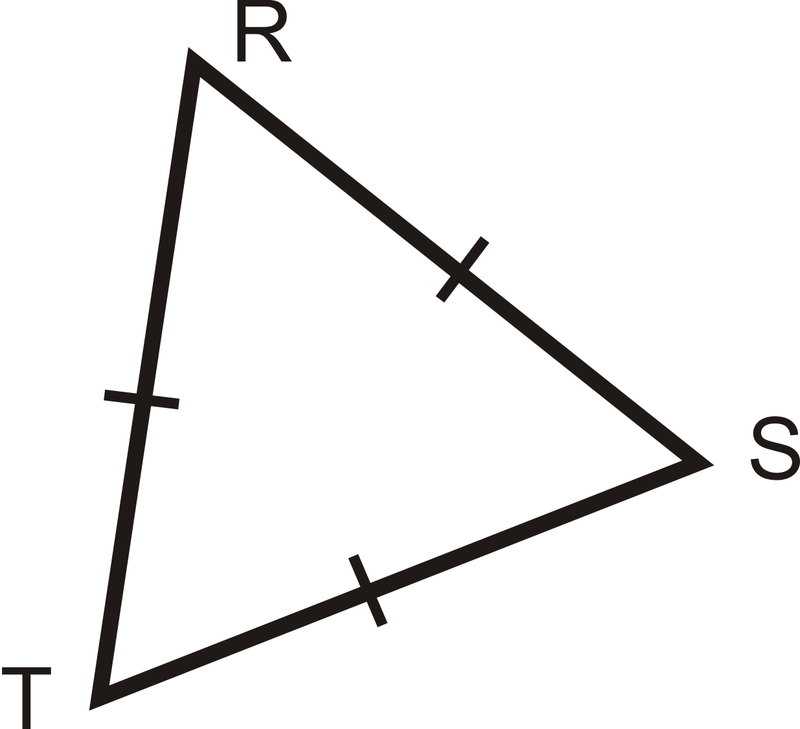
Solución
| Declaración | Razón |
|---|---|
| 1. | 1. Dado |
| 2. | 2. Teorema de ángulos de base |
| 3. | 3. Teorema de ángulos de base |
| 4. | 4. Transitivo\(PoC\) |
| 5. \(\Delta RST\)es equiangular | 5. |
| Declaración | Razón |
|---|---|
| 1. \(RT\overline{AB}\cong ST\overline{AB}\cong RS\overline{AB}\) | 1. Dado |
| 2. \(\angle R\cong \angle S\) | 2. Teorema de ángulos de base |
| 3. \(\angle T\cong \angle R\) | 3. Teorema de ángulos de base |
| 4. \(\angle T\cong \angle S\) | 4. Transitivo\(PoC\) |
| 5. \(\Delta RST\)es equiangular | 5. Definición de equiangular. |
Ejemplo\(\PageIndex{2}\)
Verdadero o falso: Todos los triángulos equiláteros son triángulos isósceles.
Solución
Esta afirmación es cierta. La definición de un triángulo isósceles es un triángulo con al menos dos lados congruentes. Dado que todos los triángulos equiláteros tienen tres lados congruentes, se ajustan a la definición de un triángulo isósceles.
Ejemplo\(\PageIndex{3}\)
Encuentra el valor de\(x\).
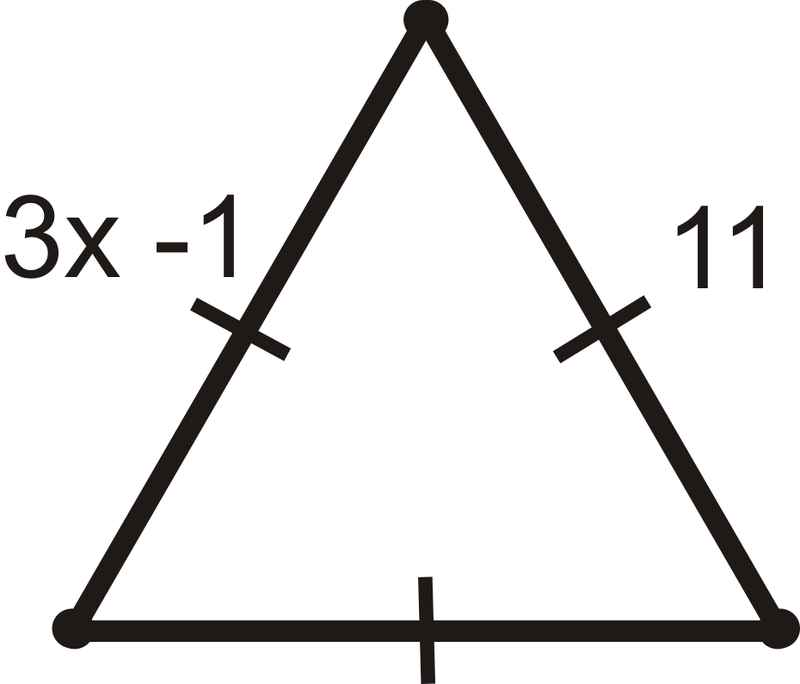
Solución
Porque se trata de un triángulo equilátero\(3x−1=11\). Resolver para\(x\).
\(\bgin{align*} 3x−1&=11 \\3x&=12 \\ x&=4 \end{align*}\)
Ejemplo\(\PageIndex{4}\)
Encuentra los valores de\(x\) y\(y\).
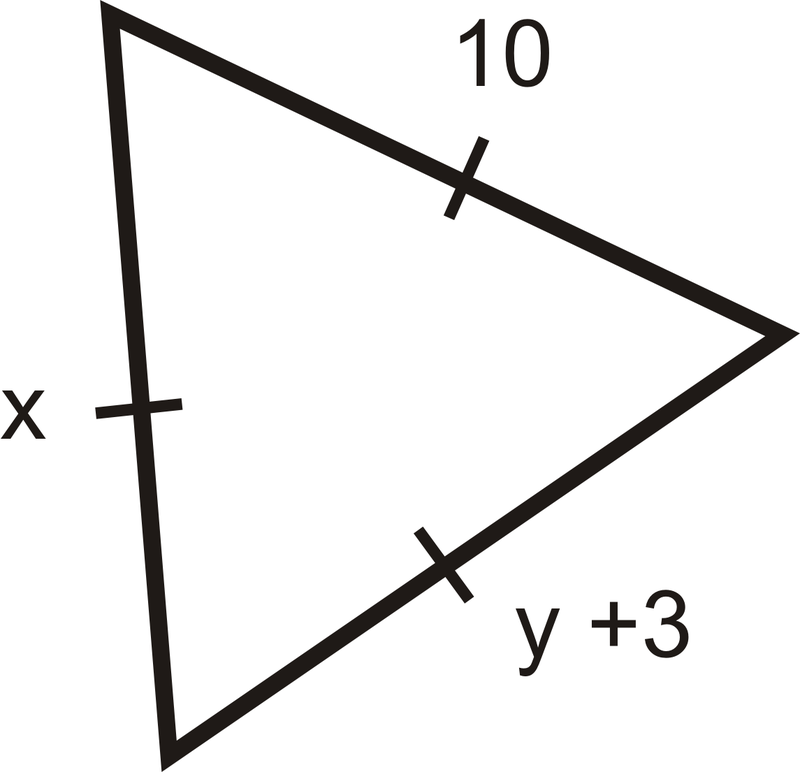
Solución
Las marcas muestran que se trata de un triángulo equilátero ya que todos los lados son congruentes. Esto significa que todas las partes deben ser iguales\(10\). Tenemos\(x=10\) y\(y+3=10\) lo que significa eso\(y=7\).
Ejemplo\(\PageIndex{5}\)
Dos lados de un triángulo equilátero son\(2x+5\) unidades y\(x+13\) unidades. ¿Cuánto dura cada lado de este triángulo?
Solución
Los dos lados dados deben ser iguales porque se trata de un triángulo equilátero. Escribe y resuelve la ecuación para\(x\).
\(\egin{align*}2x+5 &=x+13 \\ x&=8 \end{align*}\)
Para averiguar qué tan largo es cada lado, conecte 8 para\(x\) cualquiera de las expresiones originales. \(2(8)+5=21\). Cada lado es\(21\) unidades.
Revisar
Los siguientes triángulos son triángulos equiláteros. Resolver para las variables desconocidas.
-
Figura\(\PageIndex{4}\) -
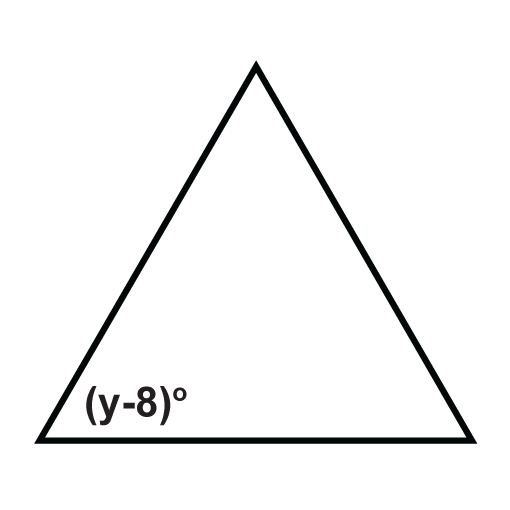
Figura\(\PageIndex{5}\) -
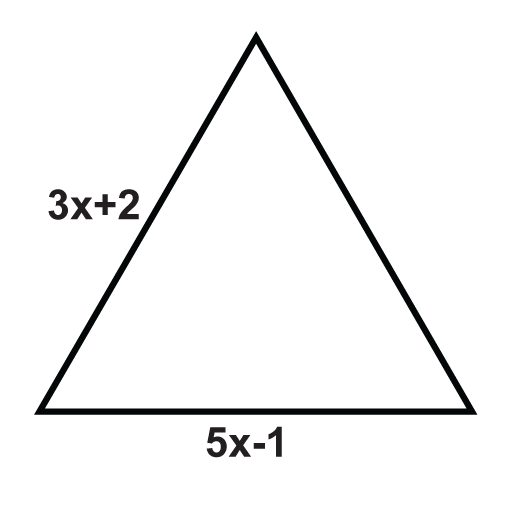
Figura\(\PageIndex{6}\) -
Figura\(\PageIndex{7}\) -
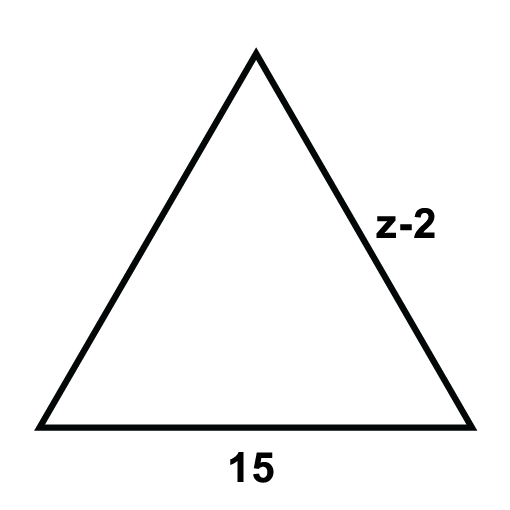
Figura\(\PageIndex{8}\) -
Figura\(\PageIndex{9}\) -
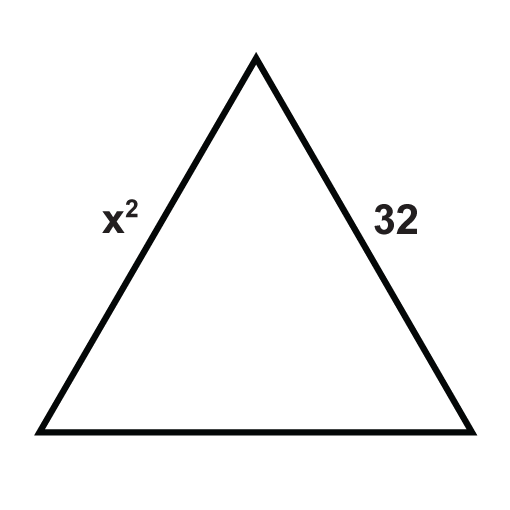
Figura\(\PageIndex{10}\) -
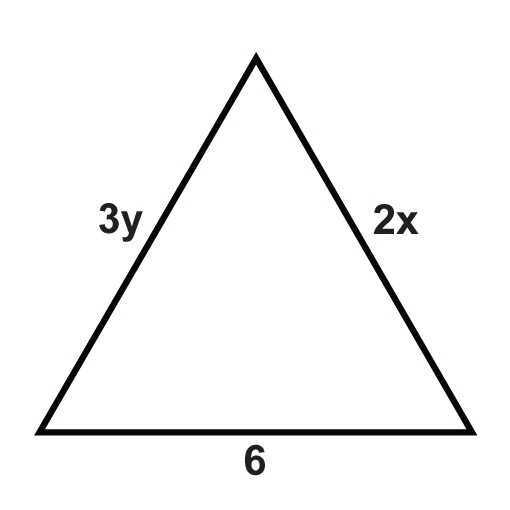
Figura\(\PageIndex{11}\) -
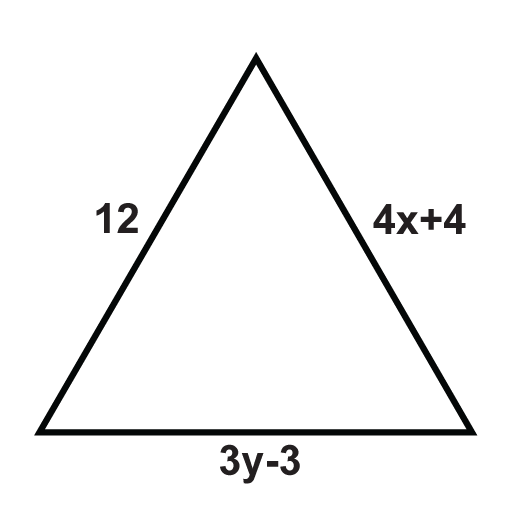
Figura\(\PageIndex{12}\) -
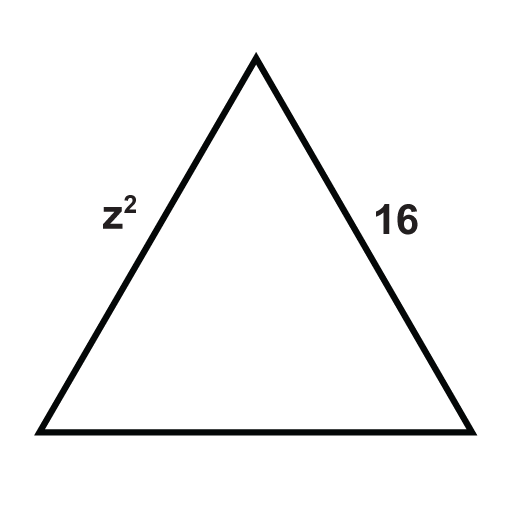
Figura\(\PageIndex{13}\) -
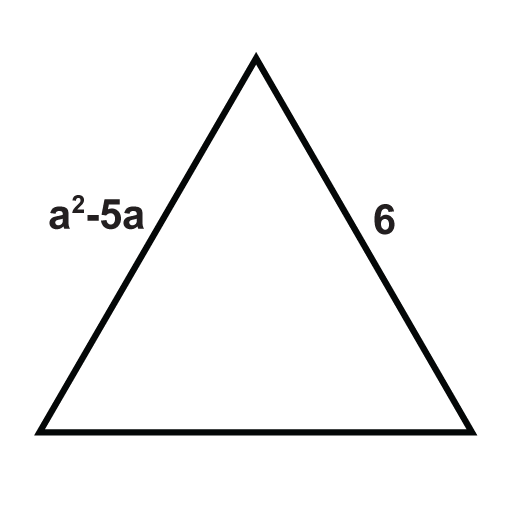
Figura\(\PageIndex{14}\) -
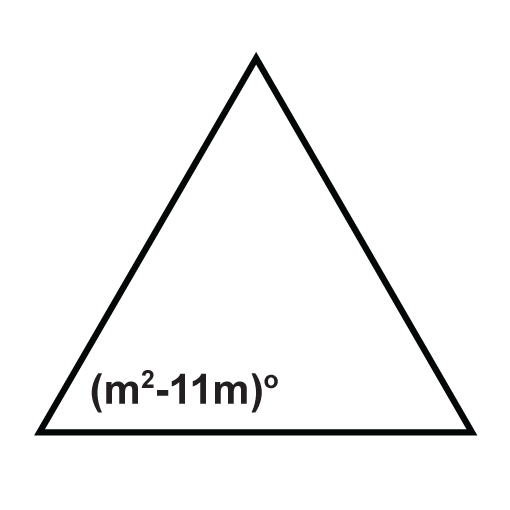
Figura\(\PageIndex{15}\) -
Figura\(\PageIndex{16}\) -
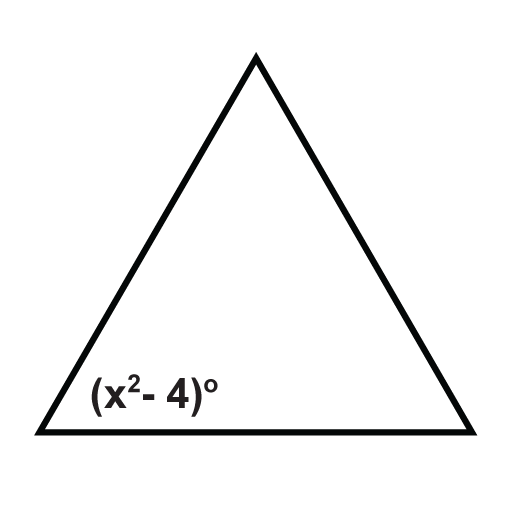
Figura\(\PageIndex{17}\) - Encuentra las medidas de\(x\) y\(y\).
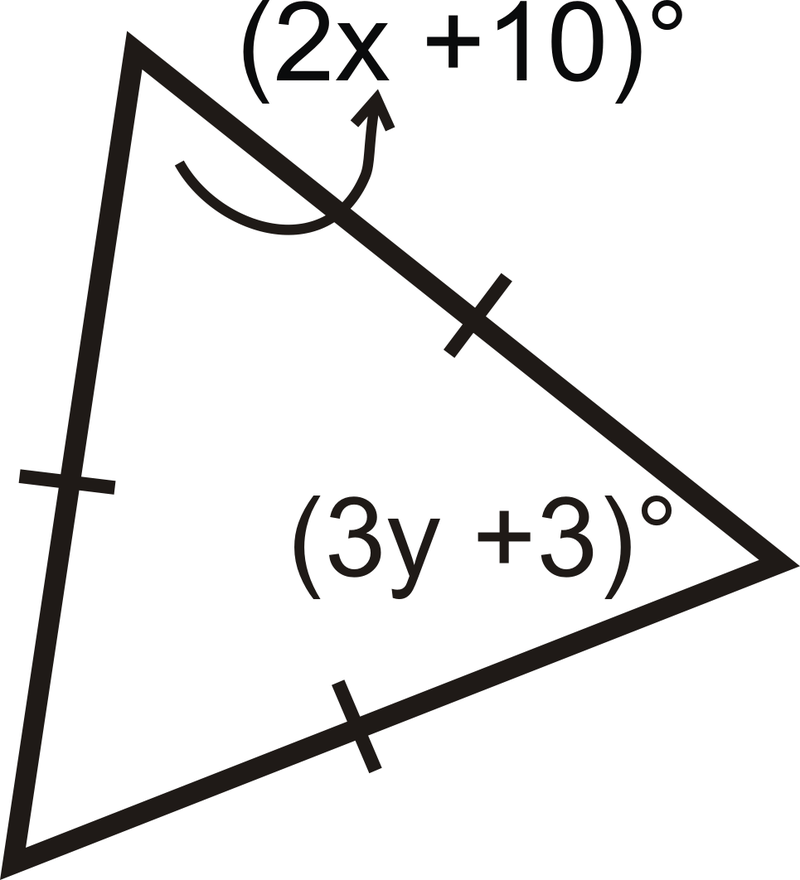
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.11.
Recursos adicionales
Elemento Interactivo
Video: Principios de los triángulos equiláteros - Básico
Actividades: Triángulos Equiláteros Preguntas de Discusión
Ayudas de estudio: Triángulos equiláteros Preguntas de Discusión
Práctica: Triángulos equiláteros
Mundo Real: Triángulos Equiláteros