4.6: Área y Perímetro de Triángulos
- Page ID
- 107475
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El área es la mitad de la base por la altura mientras que el perímetro es la suma de los lados.
La fórmula para el área de un triángulo es la mitad del área de un paralelogramo.
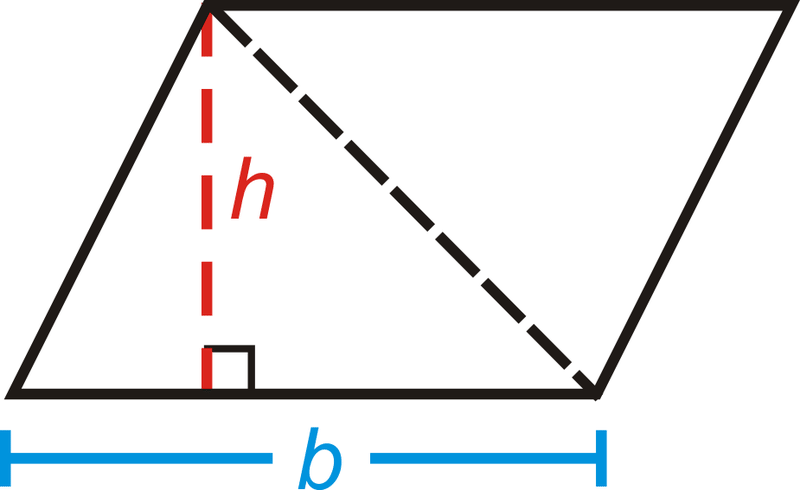
Área de un Triángulo:\(A=\dfrac{1}{2} bh\) o\(A=\dfrac{bh}{2}\).
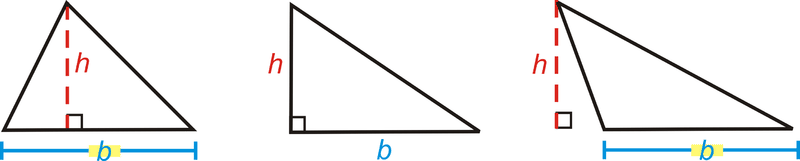
¿Y si te dieran un triángulo y el tamaño de su base y altura? ¿Cómo podrías encontrar la distancia total alrededor del triángulo y la cantidad de espacio que ocupa?
Para los Ejemplos 1 y 2, use el siguiente triángulo.
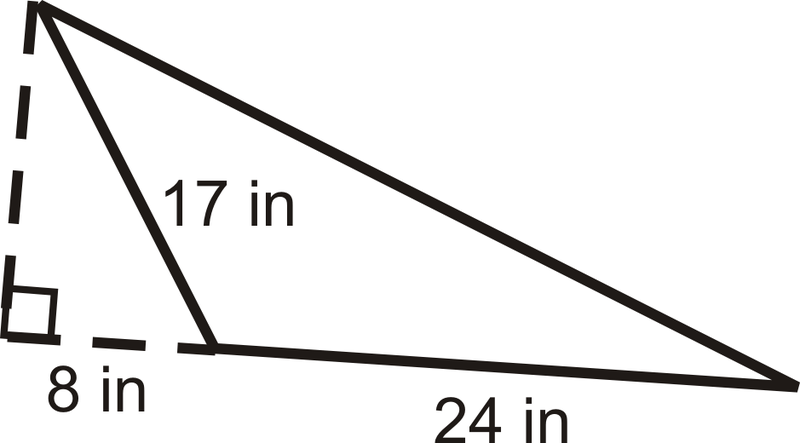
Ejemplo\(\PageIndex{1}\)
Encuentra la altura del triángulo.
Solución
Usa el Teorema de Pitágoras para encontrar la altura.
\(\begin{align*} 8^2+h^2 &=17^2 \\ h^2 &=225\\ h &=15 in \end{align*} \)
Ejemplo\(\PageIndex{2}\)
Encuentra el perímetro.
Solución
Tenemos que encontrar la hipotenusa. Usa de nuevo el Teorema de Pitágoras.
\(\begin{align*} (8+24)^2+15^2 &=h^2 \\ h^2 &=1249 \\ h &\approx 35.3 in \end{align*}\)
El perímetro es\(24+35.3+17\approx 76.3\: in\).
Ejemplo\(\PageIndex{3}\)
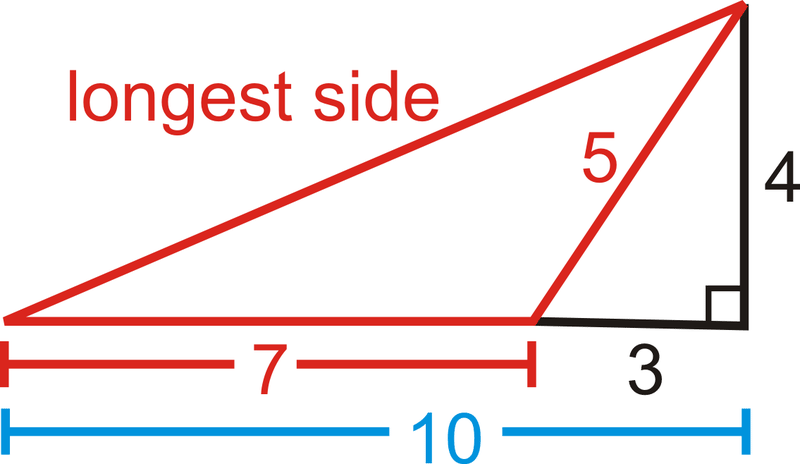
Encuentra el área del triángulo.
Solución
Para encontrar el área, necesitamos encontrar la altura del triángulo. Se nos dan dos lados del pequeño triángulo rectángulo, donde la hipotenusa es también el lado corto del triángulo obtuso.
\(\begin{align*} 3^2+h^2&=5^2 \\ 9+h^2&=25 \\ h^2&=16 \\h &=4 \\ A&=\dfrac{1}{2}(4)(7)=14 \: units^2 \end{align*}\)
Ejemplo\(\PageIndex{4}\)
Encuentra el perímetro del triángulo en el Ejemplo 3.
Solución
Para encontrar el perímetro, necesitamos encontrar el lado más largo del triángulo obtuso. Si usáramos las líneas negras en la imagen, veríamos que el lado más largo es también la hipotenusa del triángulo rectángulo con patas 4 y 10.
\(\begin{align*} 4^2+10^2&=c^2 \\ 16+100&=c^2 \\ c &=\sqrt{116}\approx 10.77 \end{align*} \)
El perímetro es\(7+5+10.77\approx 22.77\) unidades
Ejemplo\(\PageIndex{5}\)
Encuentra el área de un triángulo con base de longitud\(28 \: cm\) y altura de\(15\: cm\).
Solución
El área es\(dfrac{1}{2}(28)(15)=210\: cm^2\).
Revisar
Usa el triángulo para responder a las siguientes preguntas.
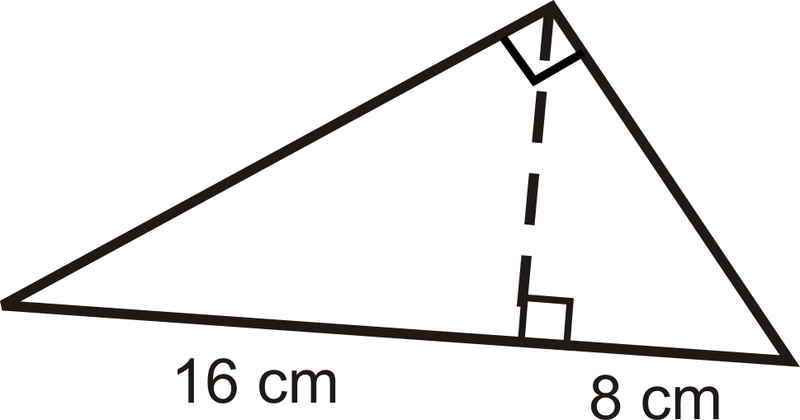
- Encuentra la altura del triángulo usando la media geométrica.
- Encuentra el perímetro.
- Encuentra la zona.
Encuentra el área de la siguiente forma.
-
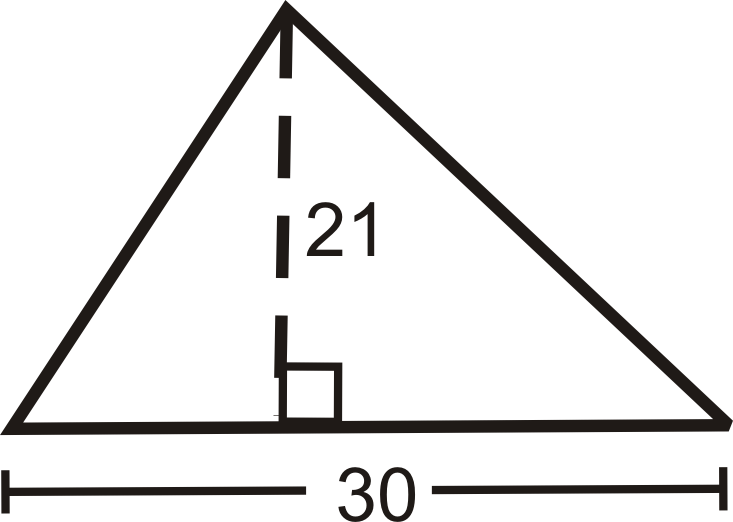
Figura\(\PageIndex{6}\) - ¿Cuál es la altura de un triángulo con área\(144\: m^2\) y una base de\(24\: m\)?
En las preguntas 6-11 vamos a derivar una fórmula para el área de un triángulo equilátero.
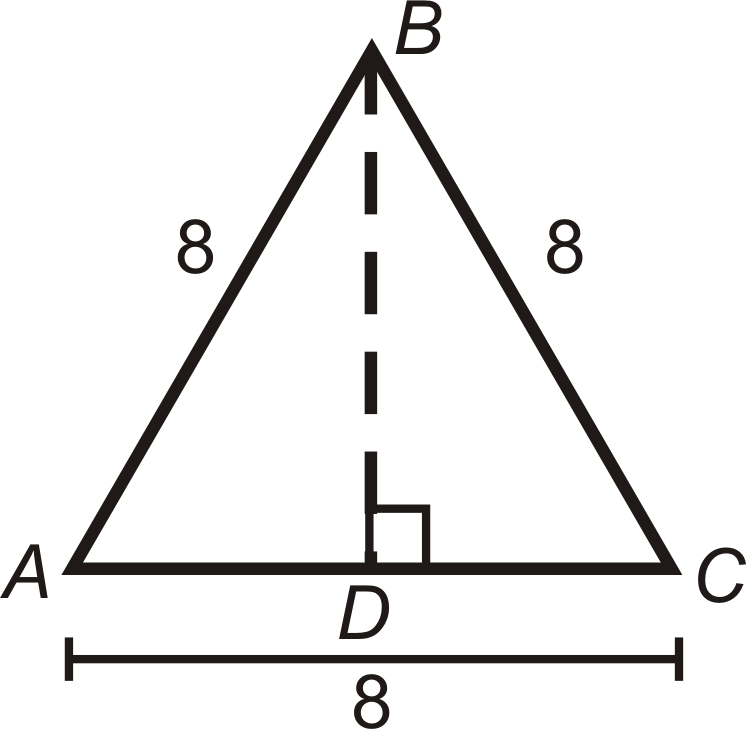
- ¿Qué tipo de triángulo es\(\Delta ABD\)? Encontrar\(AD\) y\(BD\).
- Encuentra el área de\(\Delta ABC\).
- Si cada lado es\(x\), ¿qué es\(AD\) y\(BD\)?
- Si cada lado es\(x\), encuentra el área de\(\Delta ABC\).
- Usando tu fórmula de #9, encuentra el área de un triángulo equilátero con lados de 12 pulgadas.
- Usando tu fórmula de #9, encuentra el área de un triángulo equilátero con lados de 5 pulgadas.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.3.
vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Perímetro | El perímetro es la distancia alrededor de una figura bidimensional. |
| Permetral | Las líneas perpendiculares son líneas que se cruzan en un ángulo de 90°. El producto de las pendientes de dos líneas perpendiculares es -1. |
| Ángulo recto | Un ángulo recto es un ángulo igual a 90 grados. |
| Triángulo Recto | Un triángulo rectángulo es un triángulo con un ángulo de 90 grados. |
| Área de un paralelogramo | El área de un paralelogramo es igual a la base multiplicada por la altura:\(A = bh\). La altura de un paralelogramo siempre es perpendicular a la base (los lados no son la altura). |
| Área de un Triángulo | El área de un triángulo es la mitad del área de un paralelogramo. De ahí la fórmula:\(A=\dfrac{1}{2} bh\) o\(A=\dfrac{bh}{2}\). |
Recursos adicionales
Elemento Interactivo
Video: Área de un Triángulo (Números Enteros)
Actividades: Área y Perímetro de Triángulos Preguntas de Discusión
Ayudas de estudio: Guía de estudio de triángulos y cuadriláteros
Práctica: Área y Perímetro de Triángulos
Mundo Real: Perímetro