4.7: Área del triángulo
- Page ID
- 107567
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Terry tiene dos boletos para el próximo partido en casa de su equipo favorito de futbol universitario, por lo que planea llevar a su hermano menor con él al juego. Terry quiere hacer dos banderines para el juego, por lo que compra una pieza de material en forma de rectángulo con una base de 18 pulgadas y una altura de 12 pulgadas. Terry planea dividir el material en dos triángulos. ¿Cómo puede Terry averiguar el área de cada uno de los triángulos que se cortarán del material para sus banderines?
En este concepto, aprenderás a encontrar las áreas de triángulos dadas una base y una altura.
Encontrar el área de un triángulo
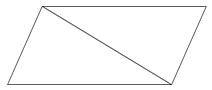
Los triángulos no son paralelogramos porque solo tienen tres lados, sino que están relacionados con paralelogramos. Eche un vistazo al paralelogramo a continuación y vea si puede averiguar la conexión.

Si miras con atención, notarás que el paralelogramo se puede dividir en dos triángulos.
Un rectángulo es un tipo de paralelogramo con cuatro ángulos rectos. También se puede dividir un rectángulo en dos triángulos.
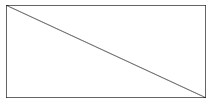
Observe que un rectángulo se divide en dos triángulos rectos, triángulos que contienen un ángulo recto.
Un cuadrado es un tipo de rectángulo con cuatro lados iguales y cuatro ángulos rectos. Un cuadrado también se puede dividir en dos triángulos rectos.
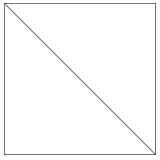
Si un paralelogramo se puede dividir en dos triángulos, entonces el área de un triángulo es la mitad del área de un paralelogramo.
Veamos cómo funciona esto.
¿Cuál es el área de este paralelogramo?

Para encontrar el área del paralelogramo, multiplica la base por la altura.
\(\begin{align*} A &=bh\\ A&=2(5)\\ A&=10 sq.\: inches.\end{align*} \)
Un paralelogramo se puede dividir en dos triángulos.
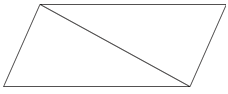
Si divides el área del paralelogramo por la mitad, eso te dará el área de uno de los triángulos.
\(10\div 2=5 sq.\: inches\)
Con base en esta información, puede escribir la siguiente fórmula para encontrar el área de un triángulo.
\(A=\dfrac{1}{2}bh\)
Un triángulo es la mitad de un paralelogramo, por lo que la fórmula para el paralelogramo multiplicado por la mitad es la fórmula para encontrar el área de un triángulo.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Terry y sus banderines deportivos.
Terry siempre ha sido fanático del fútbol Gator, por lo que está entusiasmado por asistir a uno de los juegos en casa del equipo. Ha comprado material para hacer dos banderines para el juego. El material tiene forma de rectángulo, y Terry planea dividirlo en dos triángulos para los banderines. El material tiene una base de 38 pulgadas y una altura de 30 pulgadas. Terry quiere saber el tamaño de los dos triángulos después de que corta el material. ¿Cómo puede Terry averiguar el área de cada uno de los triángulos que formarán sus banderines?
Solución
Aquí hay un vistazo a la pieza de material.
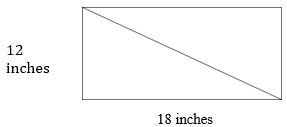
Primero, recordemos que el área de un rectángulo es base por altura y un triángulo es la mitad del área de un rectángulo.
\(\begin{align*}Base\times Height &=Area \:of \:a\: Rectangle \\ 18\times 12&=216 \\ &=216 \: square \:inches \end{align*}\)
A continuación, sustituya el valor del área por el rectángulo (o la base\ times height) en la fórmula del área del triángulo.
\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(216) \end{align*}\)
Entonces, resuelve la ecuación.
\(\begin{align*}A&=\dfrac{1}{2}(216) \\ A&=108\: square\: inches \end{align*}\)
La respuesta es que cada uno de los triángulos tendrá un área de 108 pulgadas cuadradas.
Ejemplo\(\PageIndex{2}\)
Encuentra el área del triángulo con una base de 6 pies y una altura de 5 pies.
Solución
Primero, sustituya los valores para la base y la altura en la fórmula del área del triángulo.
\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=12(6)(5) \end{align*}\)
A continuación, resolver la ecuación.
\(\begin{align*}A&=12(30) \\ A&=15\: square feet \end{align*}\)
La respuesta es de 15 pies cuadrados.
Ejemplo\(\PageIndex{3}\)
Usando el área del siguiente paralelogramo, encuentra el área de uno de los triángulos dentro del paralelogramo.
Solución
El área de un rectángulo es de 12 pulgadas cuadradas
Primero, recordemos que el área de un rectángulo es base por altura y un triángulo es la mitad del área de un rectángulo.
A continuación, sustituya el valor del área por la base y la altura en la fórmula del área del triángulo.
\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(12) \end{align*}\)
Entonces, resuelve la ecuación.
\(\begin{align*}A&=\dfrac{1}{2}(12) \\ A&=6\: square \:inches \end{align*}\)
La respuesta es de 6 pulgadas cuadradas.
Ejemplo\(\PageIndex{4}\)
Usando el área del siguiente paralelogramo, encuentra el área de uno de los triángulos dentro del paralelogramo.
Solución
El área de un paralelogramo es de 24 pies cuadrados
En primer lugar, recordemos que el área de un paralelogramo es base de tiempos de altura y un triángulo es la mitad del área de un paralelogramo.
A continuación, sustituya el valor del área por la base y la altura en la fórmula del área del triángulo.
\(\begin{align*} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(24) \end{align*}\)
Entonces, resuelve la ecuación.
\(\begin{align*} A&=\dfrac{1}{2}(24) \\ A&=12\: square\: feet \end{align*}\)
La respuesta es de 12 pies cuadrados.
Ejemplo\(\PageIndex{5}\)
Usando el área del siguiente paralelogramo, encuentra el área de uno de los triángulos dentro del paralelogramo.
Solución
El área de un paralelogramo es de 18 pies cuadrados
Primero, sustituya el valor del área por la base y la altura en la fórmula del área del triángulo.
\(\begin{align*} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(18)\end{align*}\)
Entonces, resuelve la ecuación.
\(\begin{align*} A&=\dfrac{1}{2}(18) \\ A&=9\: square\: feet \end{align*}\)
La respuesta es de 9 pies cuadrados.
Revisar
Encuentra el área de cada triángulo dadas las siguientes medidas.
-
Figura\(\PageIndex{6}\)
Base = 10 in, Altura = 4 in
-

Figura\(\PageIndex{7}\) Base = 16 metros, Altura = 10 metros
-
Figura\(\PageIndex{8}\)
Base = 8 in, Altura = 6.5 in
-
Figura\(\PageIndex{9}\)
Base = 10 cm, Altura = 7 cm
-

Figura\(\PageIndex{10}\)
Base = 5 pies, Altura = 8.5 pies
Encuentra el área de cada triángulo dada la base y la altura.
- Base = 4 in, Altura = 5 in
- Base = 6 in, Altura = 4 in
- Base = 8 ft, Altura = 7 ft
- Base = 10 metros, Altura = 8 metros
- Base = 10 metros, Altura = 5 metros
- Base = 12 pies, Altura = 14 pies
- Base = 11 pies, Altura = 6 pies
- Base = 14 pulgadas, Altura = 8 pulgadas
- Base = 22 pies, Altura = 19 pies
- Base = 30 cm, Altura = 28 cm
- Base = 18 pulgadas, Altura = 16 pulgadas
- Base = 13 metros, Altura = 10 metros
- Base = 18 metros, Altura = 5.5 metros
- Base = 12.5 pies, Altura = 2.5 pies
- Base = 13.75 pulgadas, Altura = 1.5 pulgadas
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.3.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Rectángulo | Un rectángulo es un cuadrilátero con cuatro ángulos rectos. |
| Cuadrado | Un cuadrado es un polígono con cuatro lados congruentes y cuatro ángulos rectos. |
Recursos adicionales
Elemento Interactivo
Video: Área de un Triángulo (Números Enteros)
Práctica: Área Triangular
Mundo real: Construyendo triángulos

