4.19: Teorema del segmento medio
- Page ID
- 107532
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Segmento medio de un triángulo une los puntos medios de dos lados y es la mitad de la longitud del lado al que es paralelo.
Un segmento de línea que conecta dos puntos medios de los lados de un triángulo se denomina segmento medio. \(\overline{DF}\)es el segmento medio entre\(\overline{AB}\) y\(\overline{BC}\).
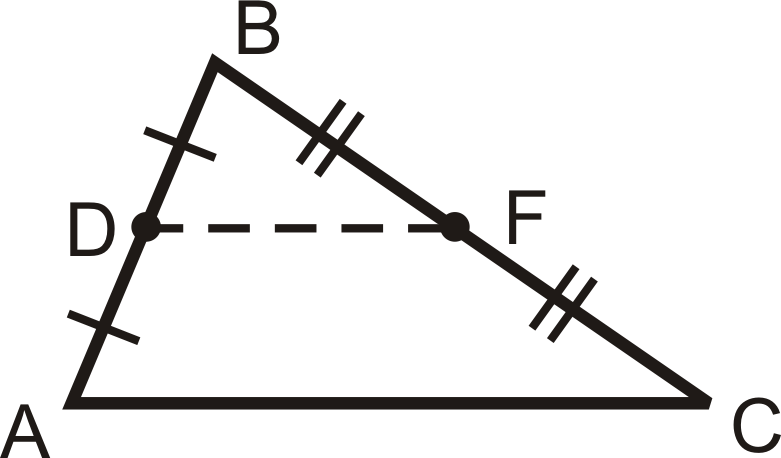
Las marcas de tic lo muestran\(D\) y\(F\) son puntos medios. \(\overline{AD}\cong \overline{DB}\)y\(\overline{BF}\cong \overline{FC}\). Por cada triángulo hay tres segmentos medios.
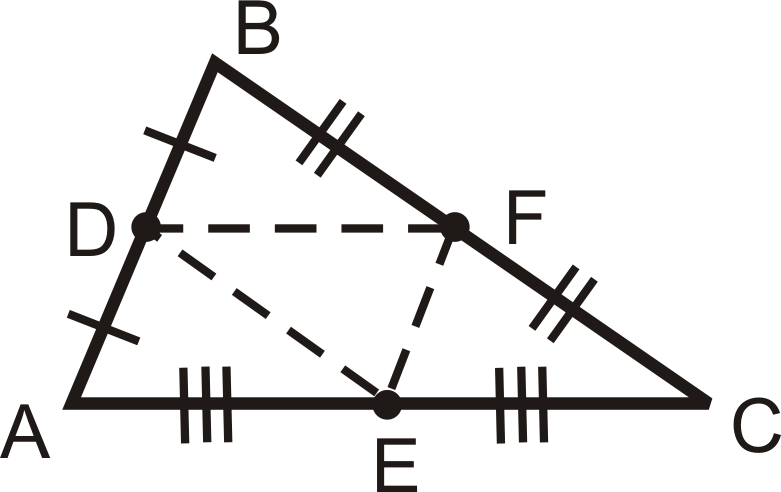
Hay dos propiedades importantes de los segmentos medios que se combinan para hacer el Teorema del Segmento Medio. El Teorema del Segmento Medio establece que el segmento medio que conecta los puntos medios de dos lados de un triángulo es paralelo al tercer lado del triángulo, y la longitud de este segmento medio es la mitad de la longitud del tercer lado. Entonces, si\(\overline{DF}\) es un segmento medio de\(\Delta ABC\), entonces\(DF=\dfrac{1}{2}AC=AE=EC\) y\(\overline{DF} \parallel \overline{AC}\).
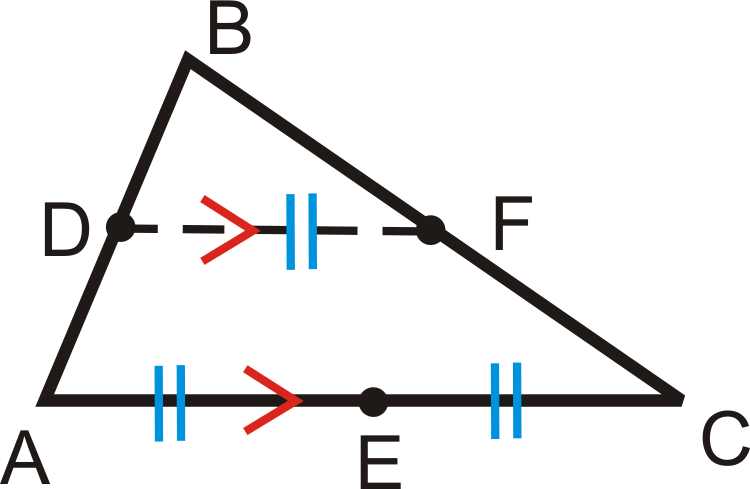
Tenga en cuenta que aquí hay dos ideas importantes. Una es que el segmento medio es paralelo a un lado del triángulo. La otra es que el segmento medio es siempre la mitad de la longitud de este lado.
¿Y si te dieran\(\Delta FGH\) y te dijeran que ese\(\overline{JK}\) era su segmento medio? ¿Cómo podrías encontrar la longitud de\(JK\) dada la longitud del tercer lado del triángulo,\(FH\)?
Ejemplo\(\PageIndex{1}\)
Encuentra el valor de\(x\) y AB. \(A\)y\(B\) son puntos medios.
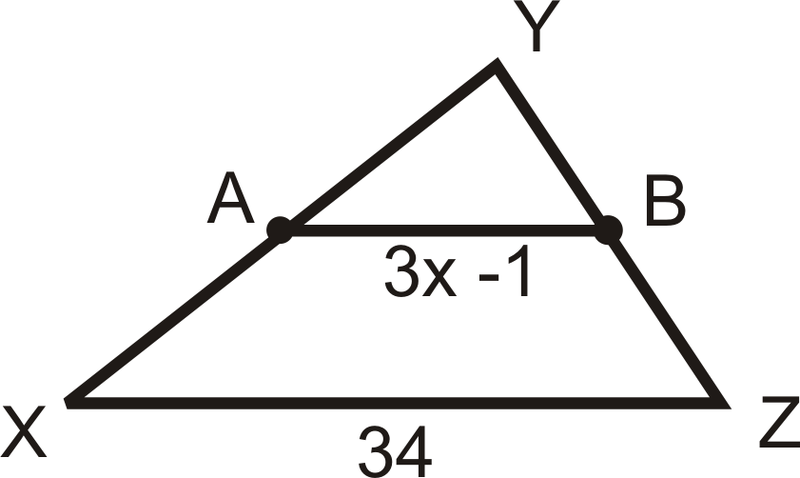
Solución
\(AB=34\div 2=17\). Para encontrar\(x\), establezca\(3x−1\) igual a 17.
\(\begin{align*} 3x−1&=17 \\ 3x&=18 \\ x&=6\end{align*}\)
Ejemplo\(\PageIndex{2}\)
Verdadero o falso: Si una línea pasa por dos lados de un triángulo y es paralela al tercer lado, entonces es un segmento medio.
Solución
Esta afirmación es falsa. Una línea que pasa por dos lados de un triángulo es solo un segmento medio si pasa por los puntos medios de los dos lados del triángulo.
Ejemplo\(\PageIndex{3}\)
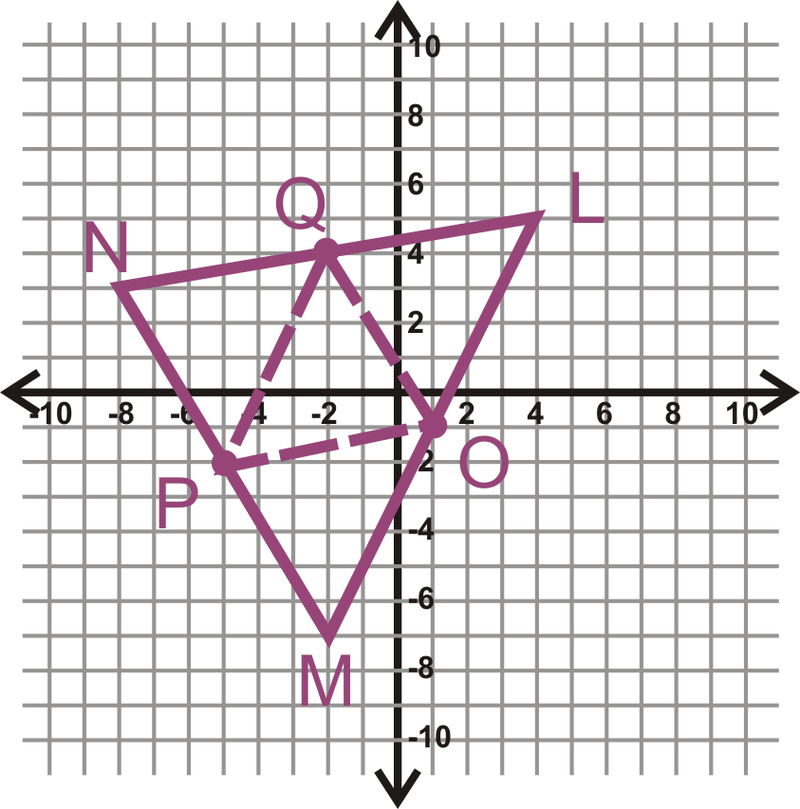
Los vértices de\(\Delta LMN\) son\(L(4,5),\: M(−2,−7)\:and\: N(−8,3)\). Encuentra los puntos medios de los tres lados, etiquétalos O, P y Q. Luego, grafica el triángulo, traza los puntos medios y dibuja los segmentos medios.
Solución
Para resolver este problema, use la fórmula de punto medio 3 veces para encontrar todos los puntos medios. Recordemos que la fórmula del punto medio es\(\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)\).
\(L\)y\(M=\left(\dfrac{4+(−2)}{2}, \dfrac{5+(−7)}{2}\right)=(1,−1),\: point\: O\)
\(M\)y\(N=\left(\dfrac{−2+(−8)}{2},\dfrac{−7+3}{2}\right)=(−5,−2),\: point\: P\)
\(L\)y\(N=\left(\dfrac{4+(−8)}{2}, \dfrac{5+3}{2}\right)=(−2,4),\: point\: Q\)
Ejemplo\(\PageIndex{4}\)

Marcar todos los segmentos congruentes\(\Delta ABC\) con puntos medios\(D\),\(E\), y\(F\).
Solución
Dibujando en los tres segmentos medios, tenemos:
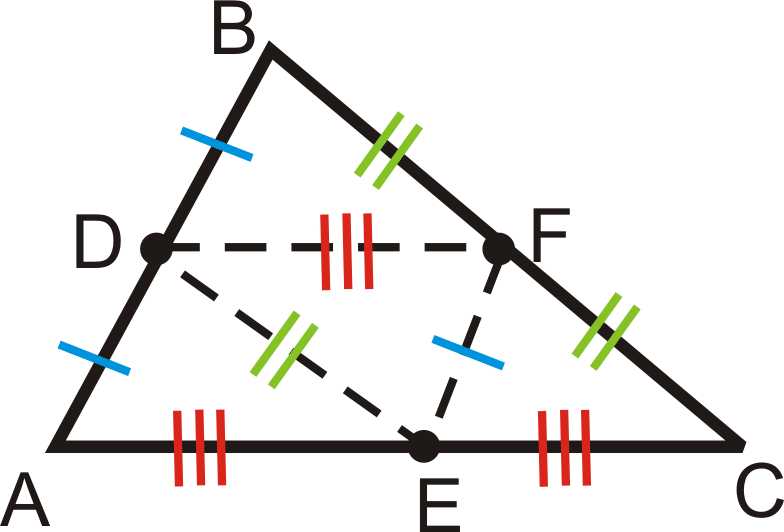
Además, esto significa que los cuatro triángulos más pequeños son congruentes por SSS.
Ahora, marque todas las líneas paralelas en\(\Delta ABC\), con puntos medios\(D\),\(E\), y\(F\).
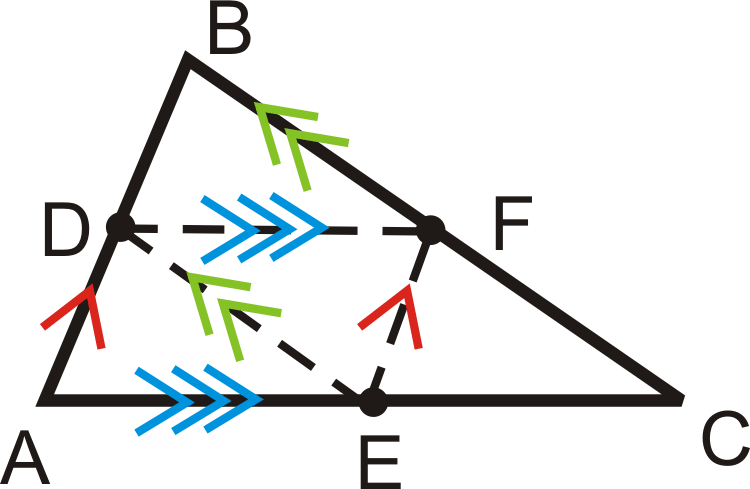
Ejemplo\(\PageIndex{5}\)
\(M\),\(N\), y\(O\) son los puntos medios de los lados de\(\Delta \(x\) YZ\).
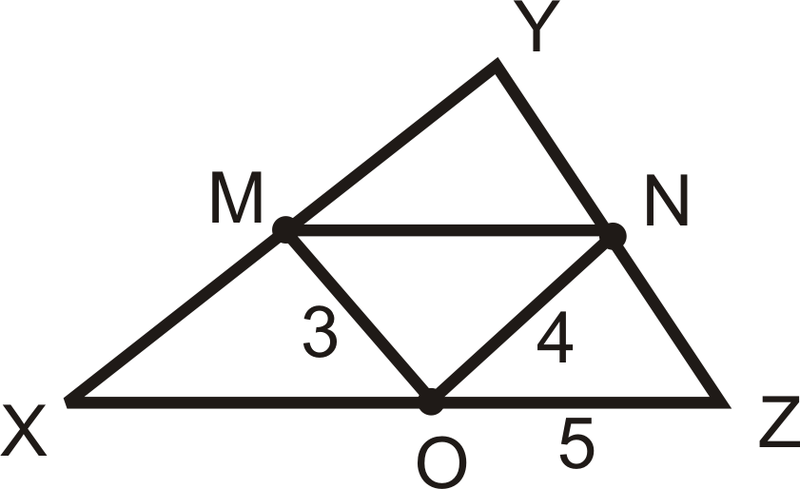
Solución
Encontrar\(MN\),\(XY\), y el perímetro de\(\Delta \(x\) YZ\).
Utilice el teorema del segmento medio:
\(MN=OZ=5\)
\(XY=2(ON)=2\cdot 4=8\)
Suma los tres lados de\(\Delta XYZ\) para encontrar el perímetro.
\(XY+YZ+XZ=2\cdot 4+2\cdot 3+2\cdot 5=8+6+10=24\)
Recuerde: Ningún segmento de línea sobre MN significa longitud o distancia.
Revisar
Determinar si cada declaración es verdadera o falsa.
- Los puntos finales de un segmento medio son puntos medios.
- Un segmento medio es paralelo al lado del triángulo que no se intersecta.
- Hay tres triángulos congruentes formados por los segmentos medios y lados de un triángulo.
- Hay tres segmentos medios en cada triángulo.
R, S, T y U son puntos medios de los lados de\(\Delta XPO\) y\(\Delta YPO\)
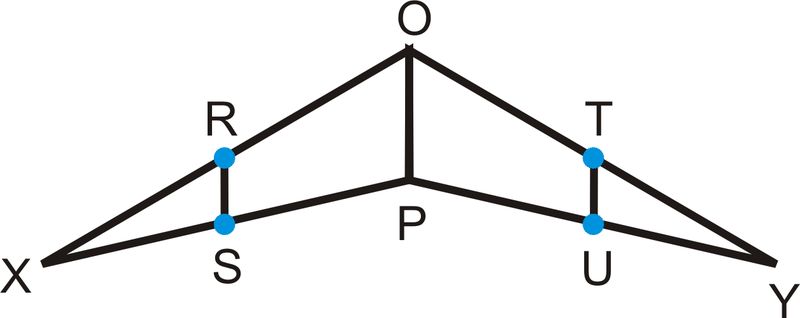
- Si\(OP=12\), encontrar\(RS\) y\(TU\).
- Si\(RS=8\), encuentra\(TU\).
- Si\(RS=2x\), y\(OP=20\), encontrar\(x\) y\(TU\).
- Si\(OP=4x\) y\(RS=6x−8\), encuentra\(x\).
Para preguntas 9-15, encuentre la (s) variable (s) indicada (s). Puede suponer que todos los segmentos de línea dentro de un triángulo son segmentos medios.
-
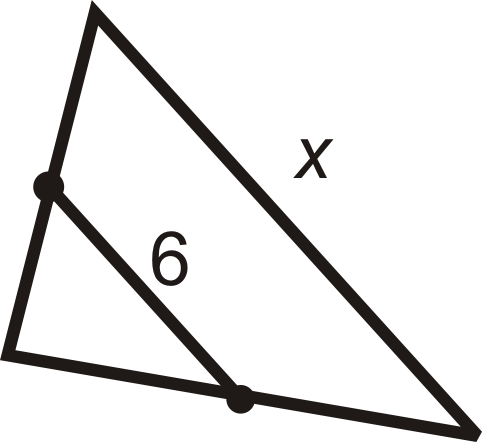
Figura\(\PageIndex{11}\) -
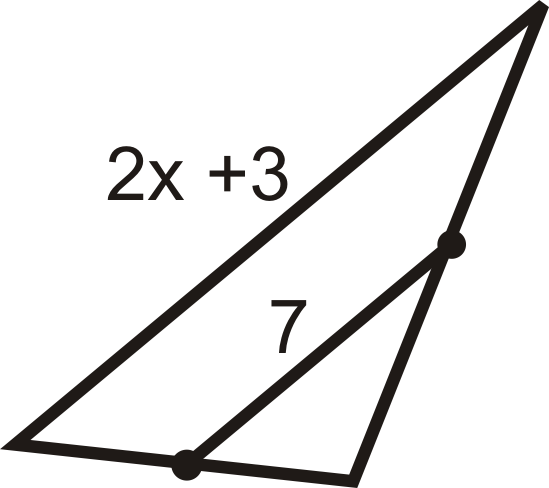
Figura\(\PageIndex{12}\) -
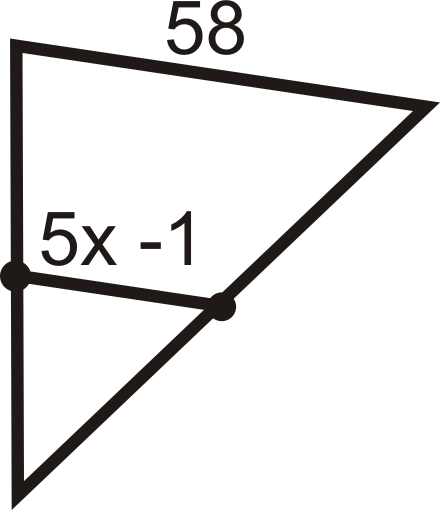
Figura\(\PageIndex{13}\) -
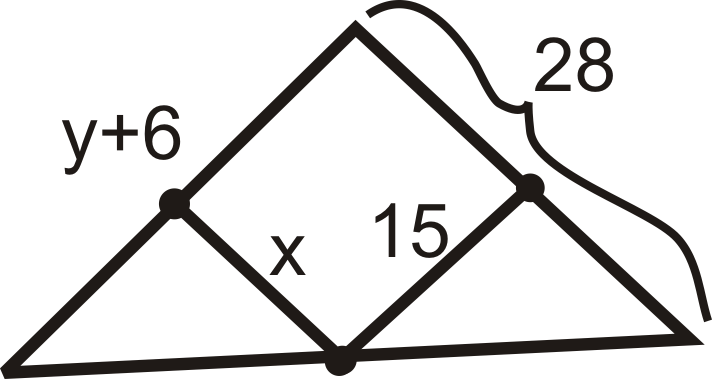
Figura\(\PageIndex{14}\) -
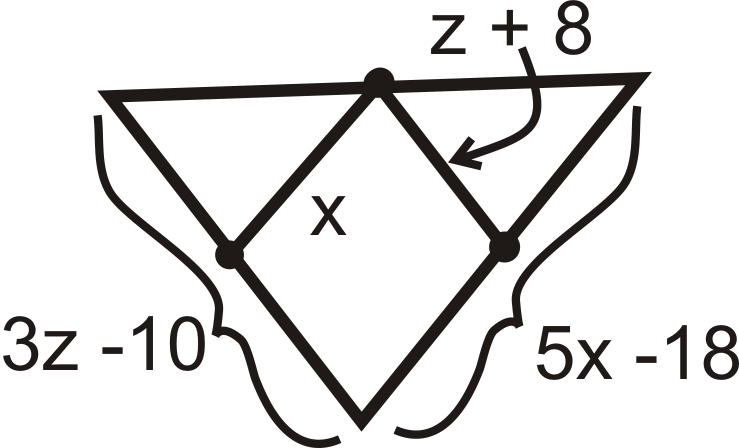
Figura\(\PageIndex{15}\) -
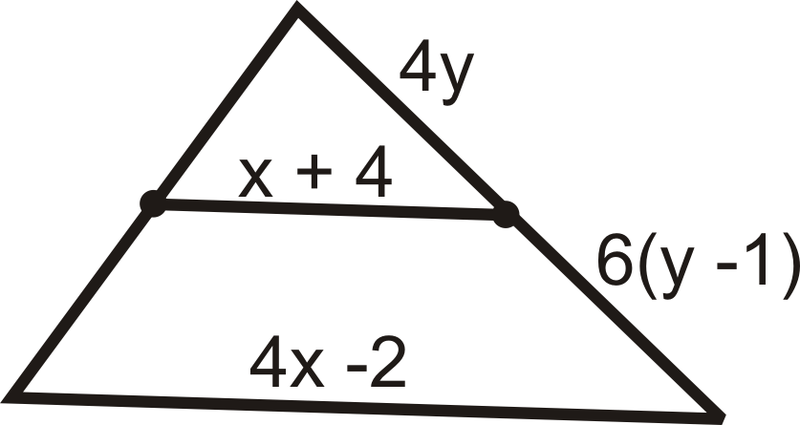
Figura\(\PageIndex{16}\) -
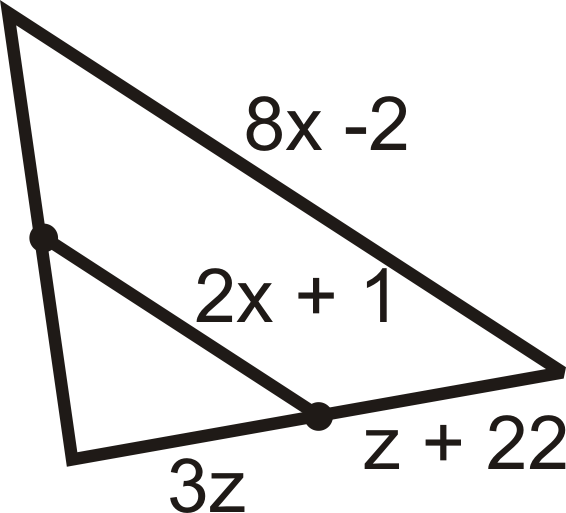
Figura\(\PageIndex{17}\) - Los lados de\(\Delta XYZ\) son 26, 38 y 42. \(\Delta ABC\)se forma uniendo los puntos medios de\(\Delta XYZ\).
- ¿Cuáles son las longitudes de los lados\(\Delta ABC\)?
- Encuentra el perímetro de\(\Delta ABC\).
- Encuentra el perímetro de\(\Delta XYZ\).
- ¿Cuál es la relación entre el perímetro de un triángulo y el perímetro del triángulo formado al conectar sus puntos medios?
Geometría de coordenadas Dados los vértices de\(\Delta ABC\) abajo encuentran los puntos medios de cada lado.
- \(A(5,−2),\: B(9,4)\: and\: C(−3,8)\)
- \(A(−10,1),\: B(4,11)\: and \:C(0,−7)\)
- \(A(−1,3),\: B(5,7)\: and\: C(9,−5)\)
- \(A(−4,−15),\: B(2,−1)\: and\: C(−20,11)\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.1.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| segmento medio | Un segmento medio conecta los puntos medios de dos lados de un triángulo o los lados no paralelos de un trapecio. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Fórmula de punto medio | La fórmula del punto medio dice que para los puntos finales\((x_1,y_1)\) y\((x_2,y_2)\), el punto medio es (\ dfrac {x_1+x_2} {2},\ frac {y_1+y_2} {2})\). |
Recursos adicionales
Vídeo: Determinar valores desconocidos usando propiedades de los segmentos medios de un triángulo
Actividades: Preguntas de discusión del teorema del segmento medio
Ayudas de Estudio: Bisectores, Medianos, Altitudes Guía de Estudio
Práctica: Teorema de segmento medio
Mundo real: Teorema de segmento medio

