4.20: Bisectores perpendiculares
- Page ID
- 107540
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Intersectar segmentos de línea en sus puntos medios y formar ángulos de 90 grados con ellos.
Teorema de bisectriz perpendicular
Una bisectriz perpendicular es una línea que intersecta un segmento de línea en su punto medio y es perpendicular a ese segmento de línea, como se muestra en la construcción a continuación.
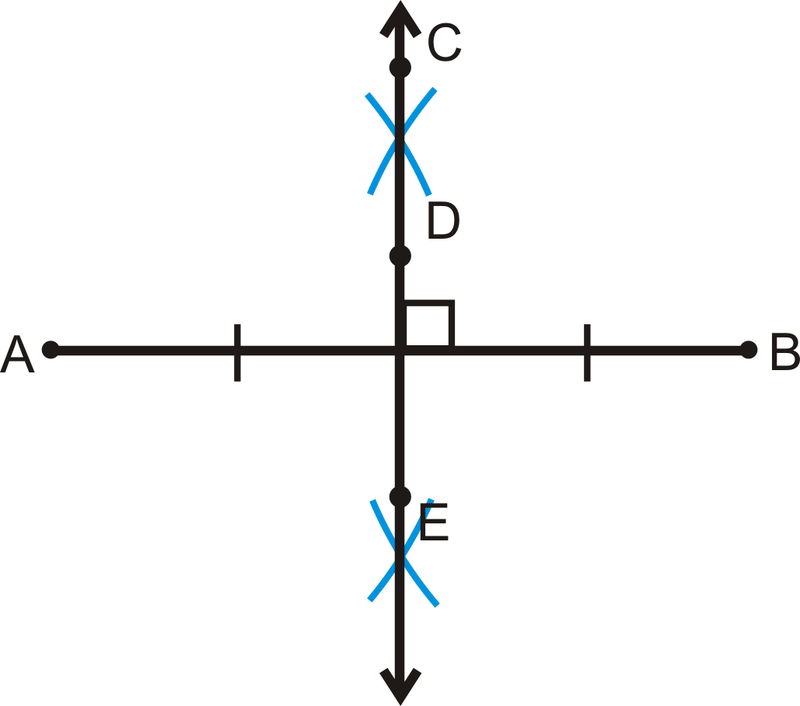
Una propiedad importante relacionada con los bisectrices perpendiculares es que si un punto está en la bisectriz perpendicular de un segmento, entonces es equidistante de los puntos finales del segmento. Esto se llama Teorema de Bisectriz Perpediente.
Si\(\overleftrightarrow{CD}\perp \overline{AB}\) y\(AD=DB\), entonces\(AC=CB\).
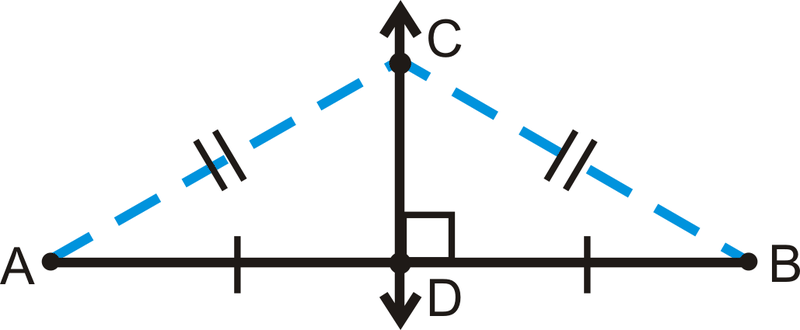
Además del teorema de bisectriz perpendicular, lo contrario también es cierto.
Teorema de bisectriz perpendicular Converse: Si un punto es equidistante de los puntos finales de un segmento, entonces el punto está en la bisectriz perpendicular del segmento.
Usando la imagen de arriba: Si\(AC=CB\), entonces\(\overleftrightarrow{CD}\perp \overline{AB}\) y\(AD=DB\).
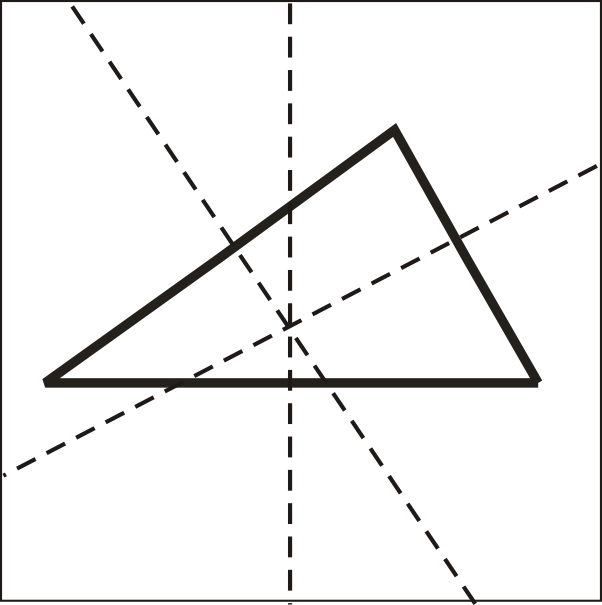
Cuando construimos bisectores perpendiculares para los lados de un triángulo, se encuentran en un punto. A este punto se le llama el circuncentro del triángulo.
¿Y si te dieran\(\Delta FGH\) y te dijeran que\(\overleftrightarrow{GJ}\) era la bisectriz perpendicular de\(\overline{FH}\)? ¿Cómo podrías encontrar la longitud de FG dada la longitud de GH\)?
Ejemplo\(\PageIndex{1}\)
\(\overleftrightarrow{OQ}\)es la bisectriz perpendicular de\(\overline{MP}\).
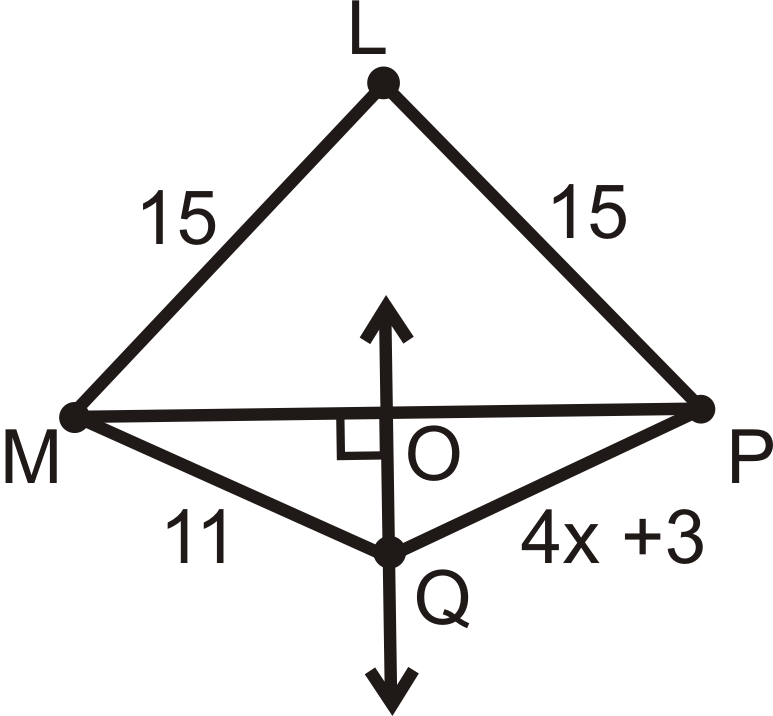
¿Qué segmentos de línea son iguales? Encuentra\(x\). ¿Está\(L\) encendido\(\overleftrightarrow{OQ}\)? ¿Cómo lo sabes?
Solución
\(ML=LP\),\(MO=OP\), y\(MQ=QP\).
\(\begin{align*} 4x+3&=11 \\ 4x&=8 \\ x&=2\end{align*} \)
Sí,\(L\) está encendido\(\overleftrightarrow{OQ}\) porque\(ML=LP\) (el Teorema Bisectorial Percepcional Converse).
Ejemplo\(\PageIndex{2}\)
Determinar si\(\overleftrightarrow{ST}\) es la bisectriz perpendicular de\(\overline{XY}\). Explique por qué o por qué no.
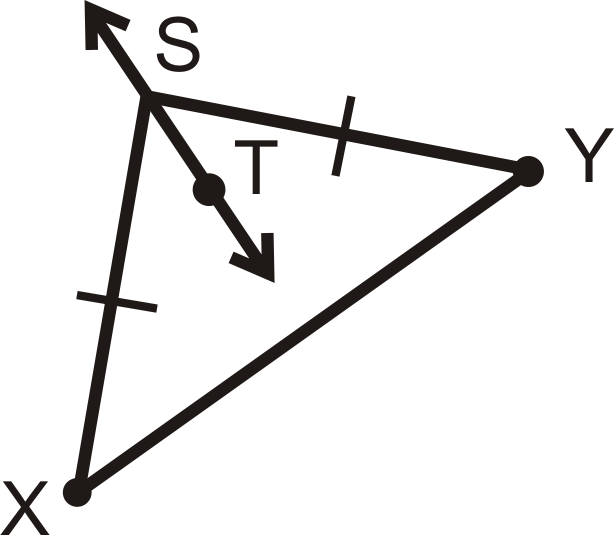
Solución
\(\overleftrightarrow{ST}\)no es necesariamente la bisectriz perpendicular de\(\overline{XY}\) porque no se da suficiente información en el diagrama. No hay manera de saber por el diagrama si\(\overleftrightarrow{ST}\) se extenderá para hacer un ángulo recto con\(\overline{XY}\).
Ejemplo\(\PageIndex{3}\)
Si\(\overleftrightarrow{MO}\) − es la bisectriz perpendicular de\(\overline{LN}\) y\(LO=8\), ¿qué es\(ON\)?
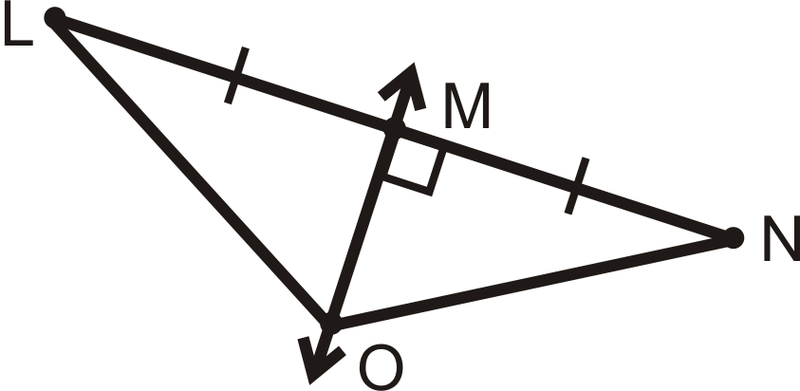
Solución
Por el teorema de bisectriz perpendicular,\(LO=ON\). Entonces,\(ON=8\).
Ejemplo\(\PageIndex{4}\)
Encuentra\(x\) y la longitud de cada segmento.
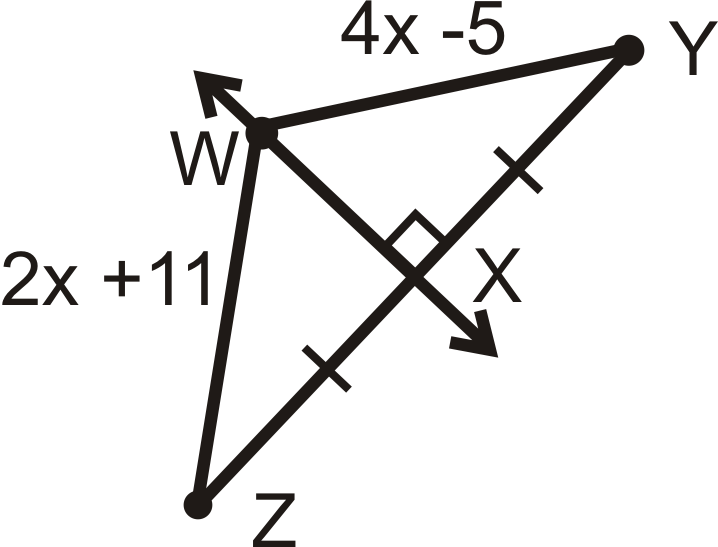
Solución
\(\overleftrightarrow{WX}\)− es la bisectriz perpendicular de\(\overline{XZ}\) y del Teorema de Bisectriz Percepcional\(WZ=WY\).
\(\begin{align*} 2x+11&=4x−5 \\ 16&=2x \\ 8&=x \end{align*}\)
\(WZ=WY=2(8)+11=16+11=27\).
Ejemplo\(\PageIndex{5}\)
Encuentra el valor de\(x\). \(m\)es la bisectriz perpendicular de\(AB\).
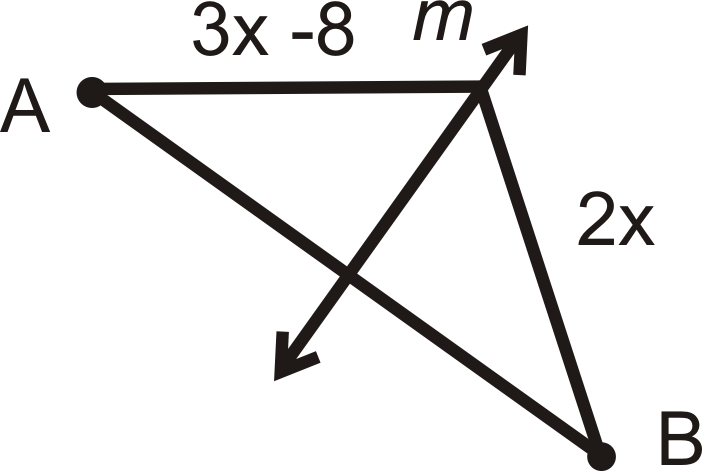
Solución
Por el teorema de bisectriz perpendicular, ambos segmentos son iguales. Configurar y resolver una ecuación.
\(\begin{align*}3x−8&=2x \\ x&=8 \end{align*} \)
Revisar
Para las preguntas 1-4, encontrar el valor de\(x\). m\) es la bisectriz perpendicular de\( AB\).
-
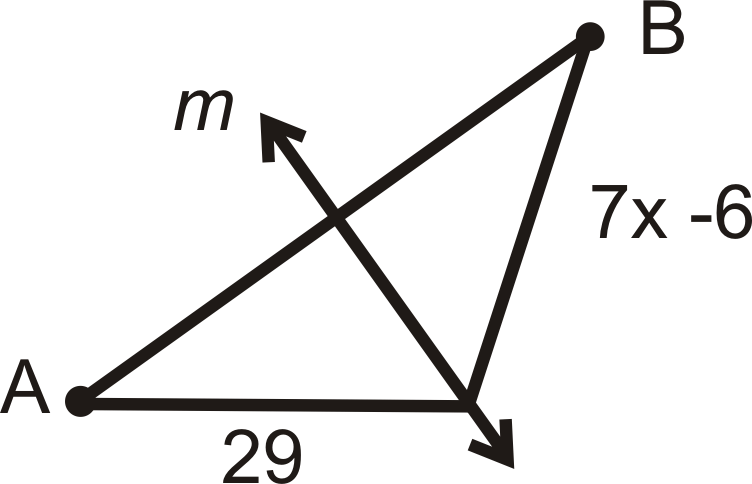
Figura\(\PageIndex{9}\) -
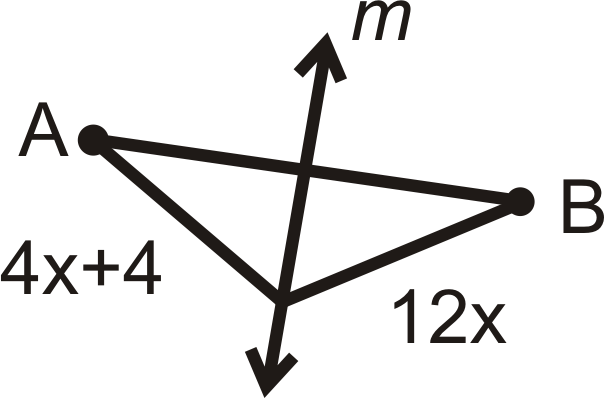
Figura\(\PageIndex{10}\) -
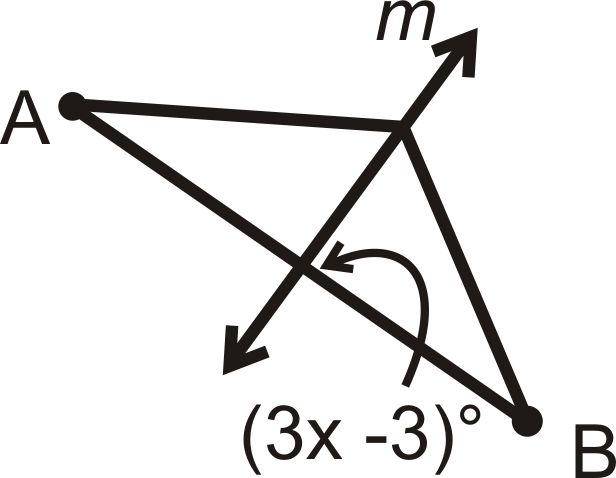
Figura\(\PageIndex{11}\) -
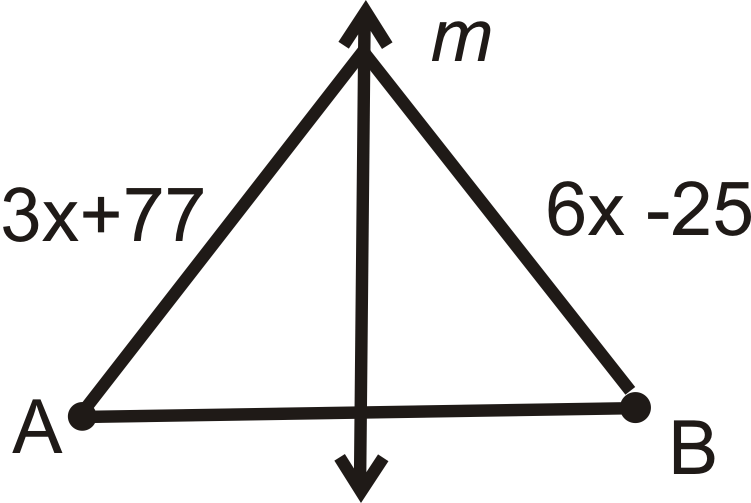
Figura\(\PageIndex{12}\)
m es la bisectriz perpendicular de\(\overline{AB}\).
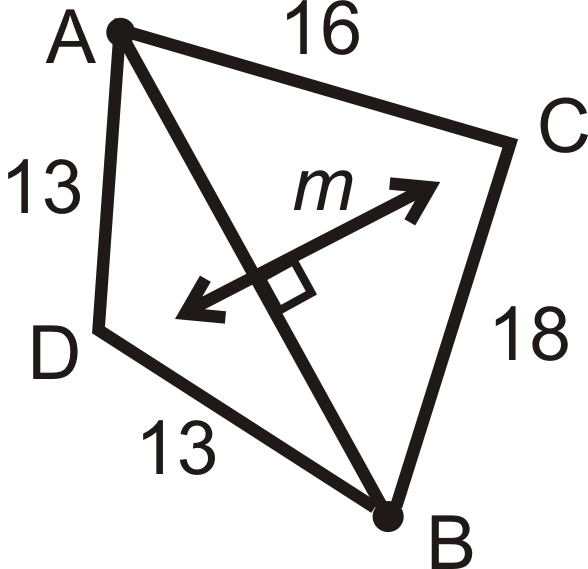
- Enumere todos los segmentos congruentes.
- ¿Está\(C\) encendido\(m\)? ¿Por qué o por qué no?
- ¿Está\(D\) encendido\(m\)? ¿Por qué o por qué no?
Para la Pregunta 8, determinar si\(\overleftrightarrow{ST}\) es la bisectriz perpendicular de\ overline {XY}\). Explique por qué o por qué no.
-
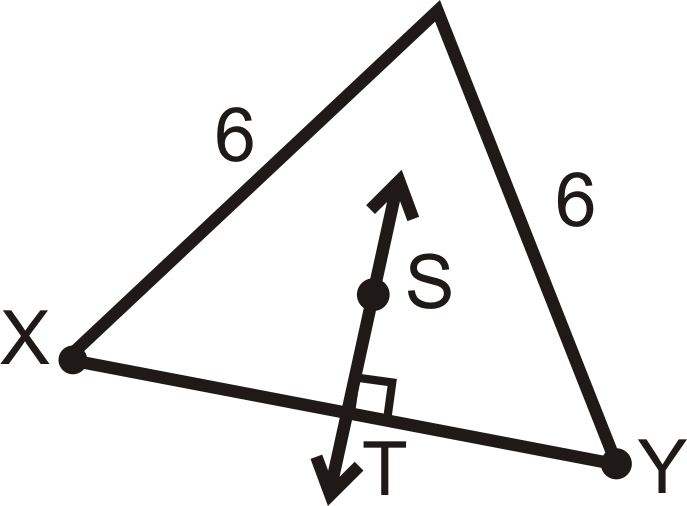Figura\(\ PageIndex {14}\) - ¿En qué tipo de triángulo pasarán todos los bisectores perpendiculares a través de los vértices del triángulo?
- Rellenar los espacios en blanco del comprobante del Teorema de Bisectriz Perjudicial.
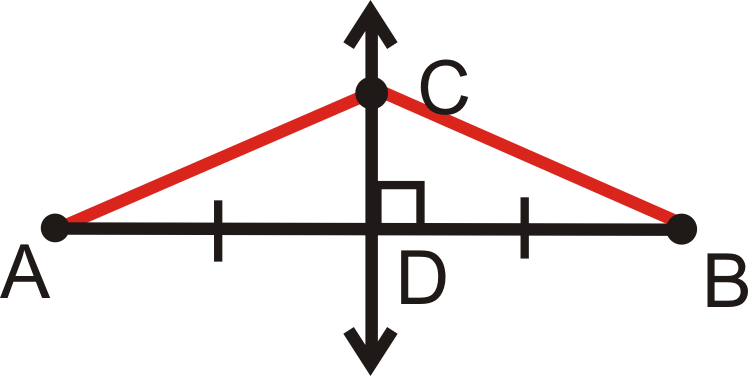
Figura\(\PageIndex{15}\)
Dado:\(\overleftrightarrow{CD}\) es la bisectriz perpendicular de\(\overline{AB}\)
Demostrar:\(\overline{AC}\cong \overline{CB}\)
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. \(D\)es el punto medio de\(\overline{AB}\) | 2. |
| 3. | 3. Definición de un punto medio |
| 4. \(\angle CDA\)y\(\angle CDB\) son ángulos rectos | 4. |
| 5. \(\angle CDA\cong \angle CDB\) | 5. |
| 6. | 6. PoC reflexivo |
| 7. \(\Delta CDA\cong \Delta CDB\) | 7. |
| 8. \(\overline{AC}\cong \overline{CB}\) | 8. |
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.2.
El vocabulario
| Término | Definición |
|---|---|
| circuncentro | El circuncentro es el punto de intersección de los bisectores perpendiculares de los lados en un triángulo. |
| bisectriz perpendicular | Una bisectriz perpendicular de un segmento de línea pasa a través del punto medio del segmento de línea e intersecta el segmento de línea en\(90^{\circ}\). |
| Teorema de bisectriz perpendicular Converse | Si un punto es equidistante de los puntos finales de un segmento, entonces el punto está en la bisectriz perpendicular del segmento. |
Recursos adicionales
Elemento Interactivo
Video: Principios de bisectores perpendiculares - Básicos
Actividades: Bisectores perpendiculares Preguntas de discusión
Ayudas para el estudio: Bisectores, Medianos, Guía de estudio de altitudes
Práctica: Bisectores perpendiculares
Mundo real: Bisectores perpendiculares