4.21: Bisectores angulares en triángulos
- Page ID
- 107553
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Construcción y propiedades de bisectores, que cortan ángulos a la mitad.
Teorema de bisectriz angular
Un ángulo bisectriz corta un ángulo exactamente por la mitad. Una propiedad importante de los bisectores angulares es que si un punto está en la bisectriz de un ángulo, entonces el punto es equidistante de los lados del ángulo. Esto se llama Teorema de Bisectriz Angular.
En otras palabras, si\(\overrightarrow{BD}\) bisectas\(\angle ABC\),\(\overrightarrow{BA}\perp FD\overline{AB}\), y,\(\overrightarrow{BC}\perp \overline{DG}\) entonces\(FD=DG\).
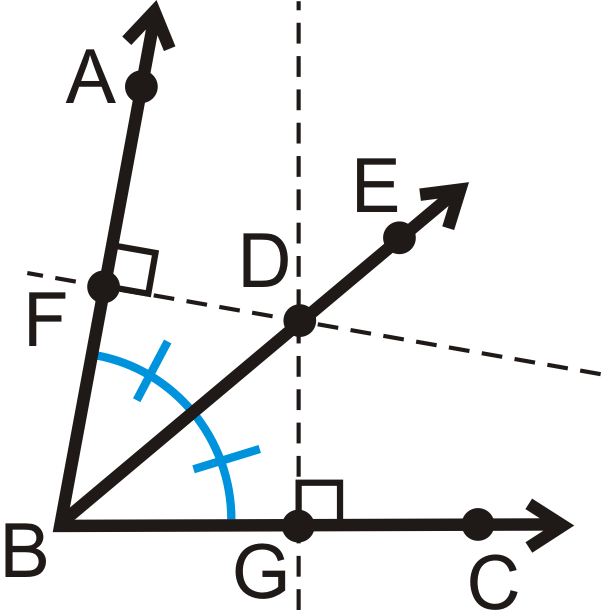
Lo contrario de este teorema también es cierto.
Ángulo Bisectriz Teorema Converse: Si un punto está en el interior de un ángulo y equidistante de los lados, entonces se encuentra en la bisectriz de ese ángulo.
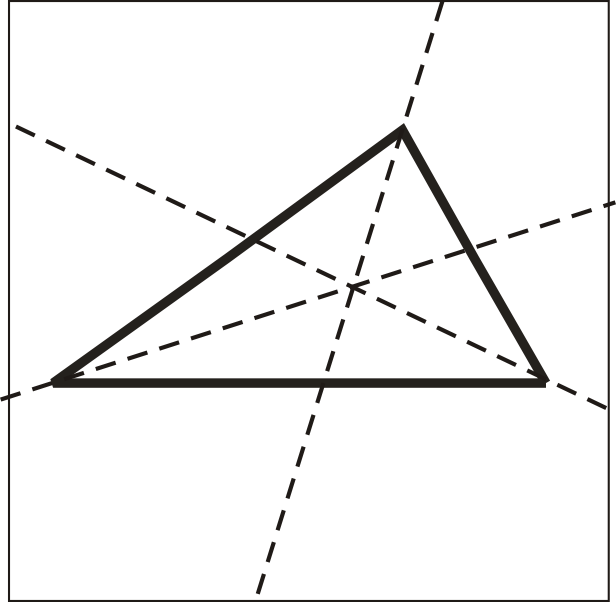
Cuando construimos bisectores angulares para los ángulos de un triángulo, se encuentran en un punto. A este punto se le llama el incentro del triángulo.
¿Y si te dijeran que ese\(\overrightarrow{GJ}\) es el ángulo bisectriz de\(\angle FGH\)? ¿Cómo encontrarías la longitud de\(FJ\) dada la longitud de\(HJ\)?
Ejemplo\(\PageIndex{1}\)
¿Hay suficiente información para determinar si\(\overrightarrow{AB}\) es el ángulo bisectriz de\(\angle CAD\)? ¿Por qué o por qué no?
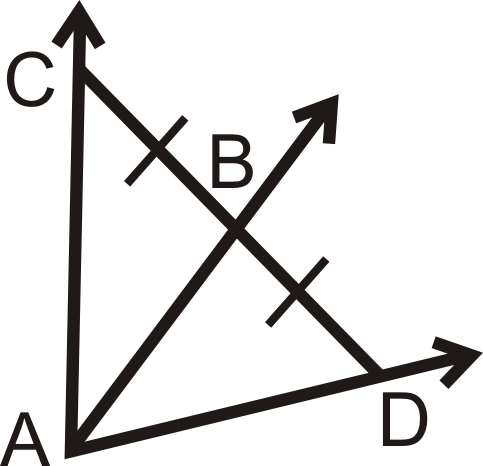
Solución
No porque no\(B\) es necesariamente equidistante de\(\overline{AC}\) y\(\overline{AD}\). No sabemos si los ángulos en el diagrama son ángulos rectos.
Ejemplo\(\PageIndex{2}\)
Un\(108^{\circ}\) ángulo es biseccionado. ¿Cuáles son las medidas de los ángulos resultantes?
Solución
Sabemos que bisectar significa cortar por la mitad, por lo que cada uno de los ángulos resultantes será la mitad de 108. La medida de cada ángulo resultante es\(54^{\circ}\).
Ejemplo\(\PageIndex{3}\)
¿Está\(Y\) en el ángulo bisectriz de\(\angle XWZ\)?
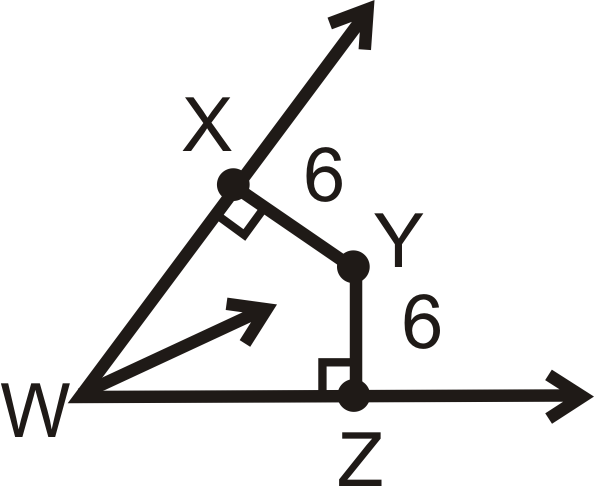
Solución
Si\(Y\) está en el ángulo bisectriz, entonces\(XY=YZ\) y ambos segmentos deben ser perpendiculares a los lados del ángulo. De las marcas que conocemos\(\overline{XY}\perp \overrightarrow{WX}\) y\(\overline{ZY}\perp \overrightarrow{WZ}\). Segundo,\(XY=YZ=6\). Entonces, sí,\(Y\) está en el ángulo bisectriz de\(\angle XWZ\).
Ejemplo\(\PageIndex{4}\)
\(\overrightarrow{MO}\)es el ángulo bisectriz de\(\angle LMN\). Encuentra la medida de\(x\).
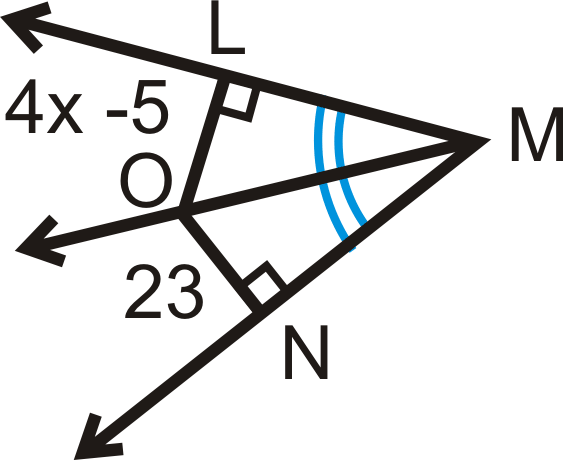
Solución
\(LO=ON\)por el Teorema de Bisectriz Angular.
\(\begin{align*} 4x−5&=23 \\ 4x&=28 \\ x&=7\end{align*} \)
Ejemplo\(\PageIndex{5}\)
\(\overrightarrow{AB}\)es el ángulo bisectriz de\(\angle CAD\). Resuelve para la variable faltante.
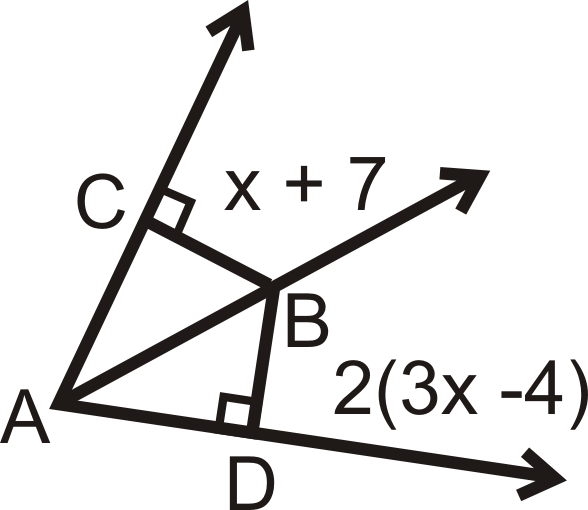
Solución
\(CB=BD\)por el Teorema de Bisectriz Angular, para que podamos configurar y resolver una ecuación para\(x\).
\(\begin{align*} x+7&=2(3x−4) \\ x+7&=6x−8 \\ 15x&=5 \\ x&=3\end{align*}\)
Revisar
Para las preguntas 1-4,\(\overrightarrow{AB}\) es el ángulo bisectriz de\(\angle CAD\). Resuelve para la variable faltante.
-
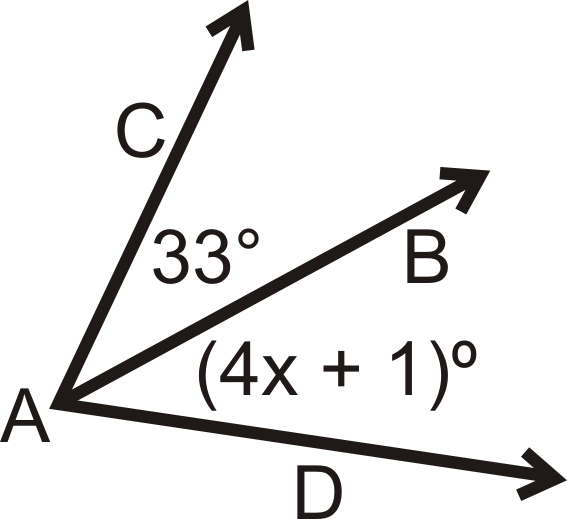
Figura\(\PageIndex{7}\) -
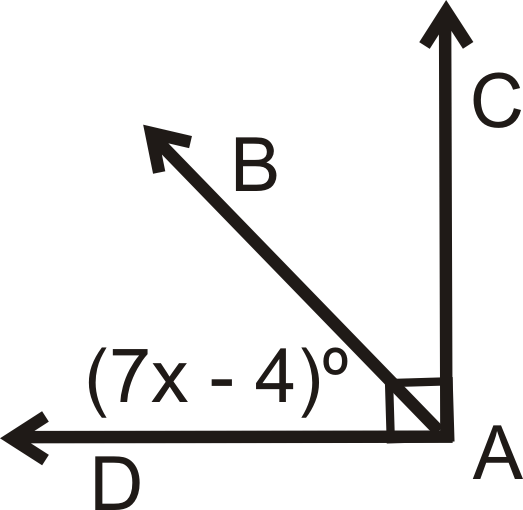
Figura\(\PageIndex{8}\) -
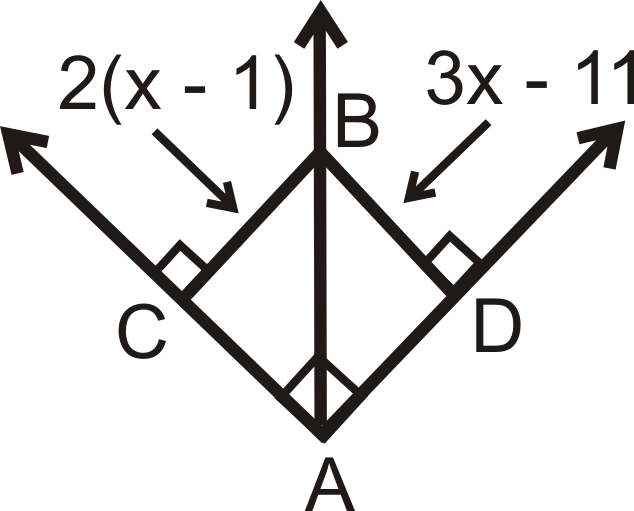
Figura\(\PageIndex{9}\) -
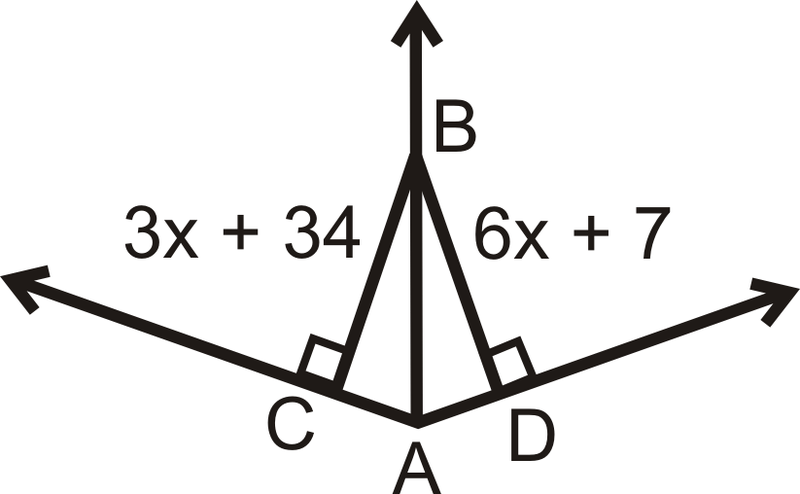
Figura\(\PageIndex{10}\)
¿Hay suficiente información para determinar si\(\overrightarrow{AB}\) es el ángulo bisectriz de\ ángulo CAD? ¿Por qué o por qué no?
-
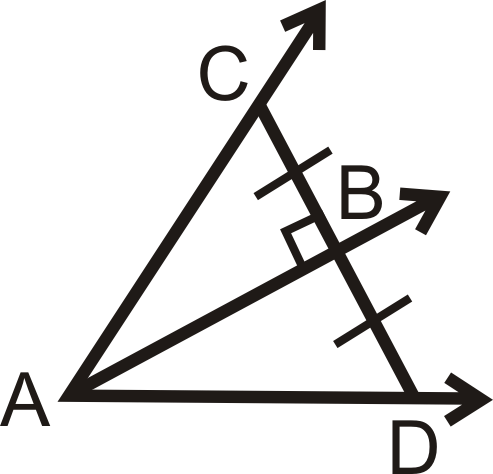
Figura\(\PageIndex{11}\) -
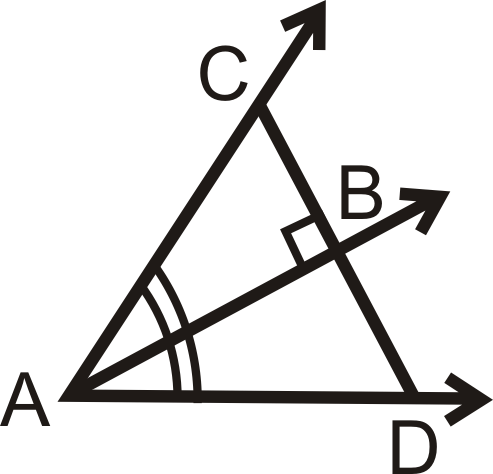
Figura\(\PageIndex{12}\)
- ¿En qué tipo de triángulo pasarán todos los bisectores angulares a través de los vértices del triángulo?
- ¿Cuál es otro nombre para los bisectores angulares de los vértices de un cuadrado?
- Dibuja en los bisectores angulares de los vértices de un cuadrado. ¿Cuántos triángulos tienes? ¿Qué tipo de triángulos son?
- Rellene los espacios en blanco en el Teorema de Bisectriz Ángulo Converse.
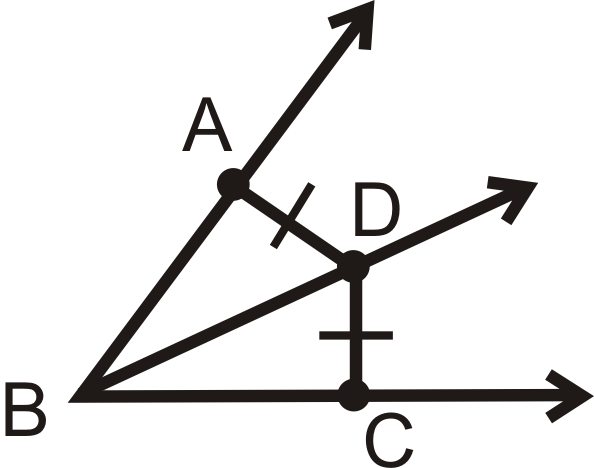
Figura\(\PageIndex{13}\)
Dado:\(\overline{AD}\cong \overline{DC}\), tal que\(AD\) y\(DC\) son las distancias más cortas a\(\overrightarrow{BA}\) y\(\overrightarrow{BC}\)
Demostrar:\(\overrightarrow{BD} bisects \angle ABC\)
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. | 2. La distancia más corta de un punto a una línea es perpendicular. |
| 3. \(\angle DAB \)y\(\angle DCB\) son ángulos rectos | 3. |
| 4. \(\angle DAB\cong \angle DCB\) | 4. |
| 5. \(\overline{BD}\cong \overline{BD}\) | 5. |
| 6. \(\Delta ABD\cong \Delta CBD\) | 6. |
| 7. | 7. CPCTC |
| 8. \(\overrightarrow{BD}\)bisectos\(\angle ABC\) | 8. |
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.3.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| bisectriz angular | Una bisectriz angular es un rayo que divide un ángulo en dos ángulos congruentes y más pequeños. |
| Teorema de bisectriz angular | El teorema de la bisectriz del ángulo establece que si un punto está en la bisectriz de un ángulo, entonces el punto es equidistante de los lados del ángulo. |
| Ángulo Bisectriz Teorema Converse | El teorema de ángulo bisectriz converse establece que si un punto está en el interior de un ángulo y equidistante de los lados, entonces se encuentra en la bisectriz de ese ángulo. |
| incenter | El incentro es el punto de intersección de los bisectores angulares en un triángulo. |
Recursos adicionales
Elemento Interactivo
Video: Ejemplos: Resolver valores desconocidos usando propiedades de bisectores angulares
Actividades: Bisectores angulares en triángulos Preguntas de discusión
Ayudas de Estudio: Bisectores, Medianos, Altitudes Guía de Estudio
Práctica: Bisectores angulares en triángulos
Mundo real: Bisectores perpendiculares