4.22: Concurrencia y Construcciones
- Page ID
- 107523
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Construcciones relacionadas con teoremas que involucran circuncentros y otros puntos de intersección de tres o más líneas.
Dado un triángulo, ¿cuál es la diferencia entre el círculo inscrito del triángulo y el círculo circunscrito del triángulo?
Círculos de Triángulos Inscritos y Circunscritos
Dado un triángulo, un círculo inscrito es el círculo más grande contenido dentro del triángulo. El círculo inscrito tocará cada uno de los tres lados del triángulo exactamente en un punto. El centro del círculo inscrito en un triángulo es el incentro del triángulo, el punto donde se encuentran los bisectores angulares del triángulo.
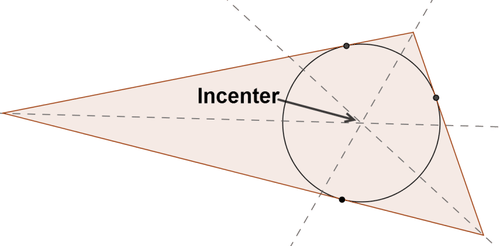
Para construir el círculo inscrito:
- Construir el incenter.
- Construye una línea perpendicular a un lado del triángulo que pasa por el incenter. El segmento que conecta el incenter con el punto de intersección del triángulo y la línea perpendicular es el radio del círculo.
- Construye un círculo centrado en el incentro con el radio que se encuentra en el paso 2.
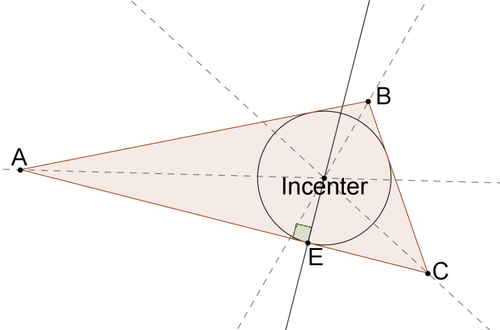
Los pasos para construir el círculo inscrito para un triángulo dado se explorarán en los siguientes problemas.
Dado un triángulo, el círculo circunscrito es el círculo que pasa por los tres vértices del triángulo. El centro del círculo circunscrito es el circuncentro del triángulo, el punto donde se encuentran los bisectores perpendiculares de los lados.
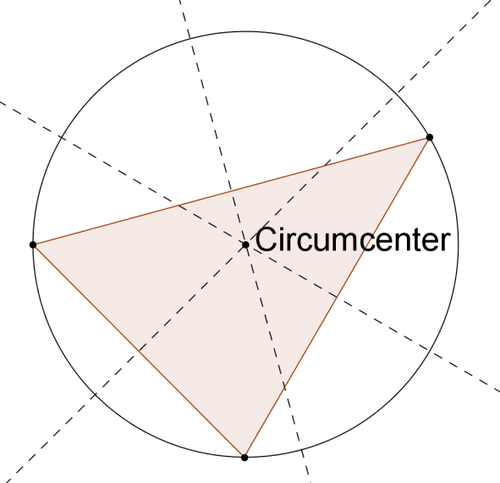
Para construir el círculo circunscrito:
- Construir el circuncentro.
- Construye un círculo centrado en el circuncentro que pasa por uno de los vértices. Este mismo círculo debería pasar por los tres vértices.
Los pasos para construir el círculo circunscrito para un triángulo dado se explorarán en la sección Ejemplos.
Construcción de bisectores angulares
Dibuja un triángulo. Construir los bisectores angulares de dos de sus ángulos. ¿Por qué el punto de intersección de los dos bisectores angulares es el incentro del círculo?
Usa tu brújula y recto para construir el ángulo bisectriz de uno de los ángulos.
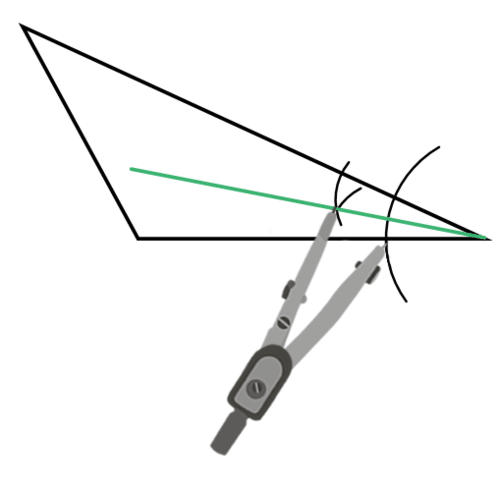
Repita con un segundo ángulo.
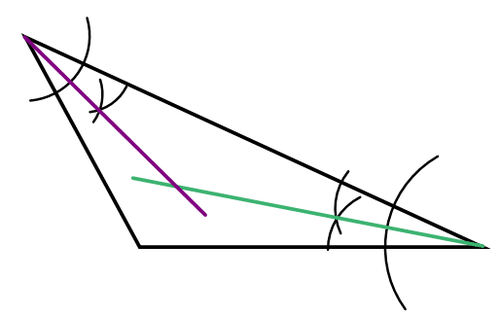
El punto de intersección de los bisectores angulares es el incentro. No es necesario construir los tres bisectores angulares porque todos se encuentran en un mismo punto. El tercer ángulo bisectriz no proporciona ninguna nueva información.
Construcción de líneas perpendiculares
Construye una línea perpendicular a un lado del triángulo que pasa por el incentro del triángulo.
Usa tu brújula y recto para construir una línea perpendicular a un lado del triángulo que pasa por el incenter.
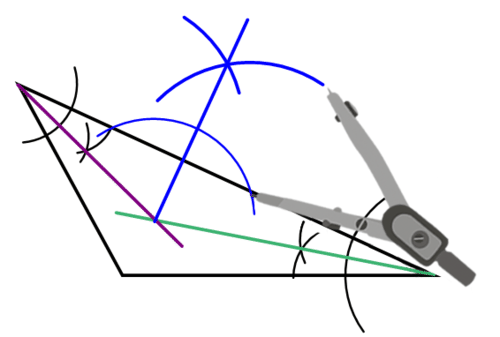
Construyendo Círculos Inscriptos
Construir un círculo centrado en el incentro que pase por el punto de intersección del lado del triángulo y la línea perpendicular desde el problema anterior.
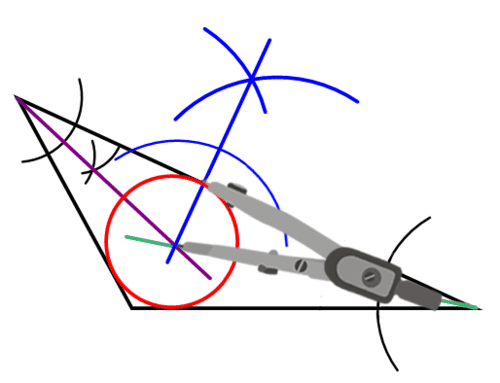
Tenga en cuenta que este círculo toca cada lado del triángulo exactamente una vez.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le preguntó cuál es la diferencia entre el círculo inscrito del triángulo y el círculo circunscrito del triángulo.
Solución
El círculo inscrito de un triángulo está dentro del triángulo. El círculo circunscrito de un triángulo está fuera del triángulo.
Ejemplo\(\PageIndex{2}\)
Dibuja un triángulo. Construir los bisectores perpendiculares de dos de sus lados. ¿Por qué el punto de intersección de los dos bisectores perpendiculares es el circuncentro del círculo?
Solución
Usa tu brújula y recto para construir la bisectriz perpendicular de un lado.
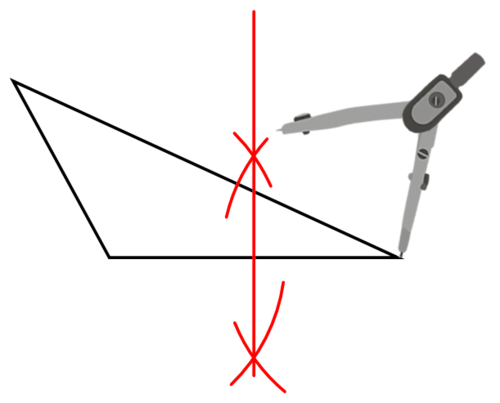
Repita con un segundo lado.
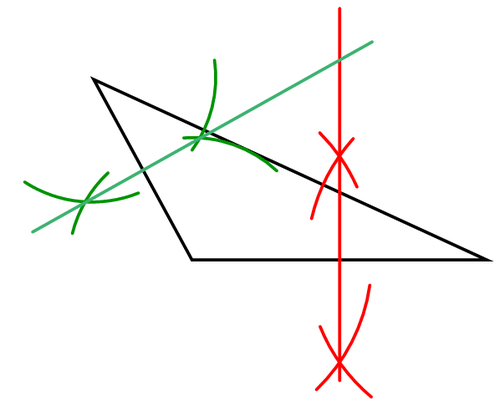
El punto de intersección de los bisectores perpendiculares es el circuncentro. No es necesario construir los tres bisectores perpendiculares porque todos se encuentran en un mismo punto. La tercera bisectriz perpendicular no proporciona ninguna nueva información.
Ejemplo\(\PageIndex{3}\)
Continúa con tu triángulo desde #2. Construir el círculo circunscrito del triángulo.
Solución
Construye un círculo centrado en el circuncentro que pasa por uno de los vértices del triángulo. Este círculo debería pasar por los tres vértices.
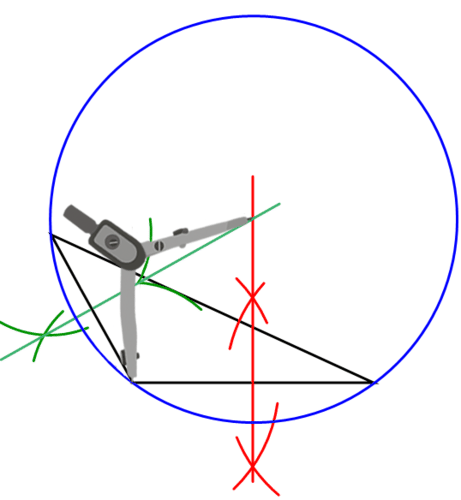
Ejemplo\(\PageIndex{4}\)
Justifica la afirmación: La hipotenusa de un triángulo rectángulo será un diámetro del círculo circunscrito del triángulo.
Solución
Cada uno de los ángulos que componen un triángulo se convierten en ángulos inscritos del círculo circunscrito. Un\(90^{\circ}\) ángulo interceptará un arco de\(180^{\circ}\), que es medio círculo. Por lo tanto, el lado opuesto al\(90^{\circ}\) ángulo del triángulo debe ser un diámetro del círculo.
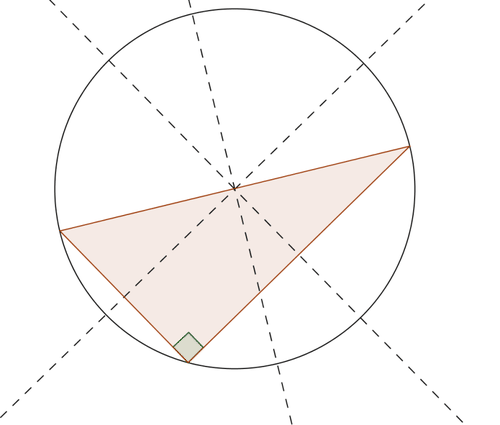
Revisar
1. Dibuja un triángulo y construye el ángulo bisectriz de dos de sus ángulos.
2. Continúa con tu triángulo desde #1. Construye una línea perpendicular a un lado del triángulo que pasa por el incentro del triángulo.
3. Continúa con tu triángulo desde #1 y #2. Construye el círculo inscrito del triángulo.
4. ¿Por qué no fue necesario construir la bisectriz angular de los tres ángulos del triángulo?
5. Explique por qué el incenter es equidistante de cada uno de los lados del triángulo.
6. Dibuja un triángulo y construye la bisectriz perpendicular de dos de sus lados.
7. Continúa con tu triángulo desde #5. Construir el círculo circunscrito del triángulo.
8. Explique por qué el circuncentro es equidistante de cada uno de los vértices del triángulo.
Trabajas vendiendo comida de un camión de comida en un parque local. Desea posicionar su camioneta de manera que esté a la misma distancia de cada una de las tres ubicaciones que se muestran en el mapa a continuación.

9. ¿El punto de interés es el incentro o el circuncentro?
10. Encuentra el punto en el mapa que es equidistante de cada una de las tres ubicaciones.
11. ¿Cómo podrías doblar el mapa en dos lugares para encontrar el punto equidistante de cada una de las tres ubicaciones?
Se va a construir una nueva escuela primaria en tu ciudad. El plan es construir la escuela para que esté a la misma distancia de cada una de las tres carreteras principales que se muestran en el mapa de abajo.
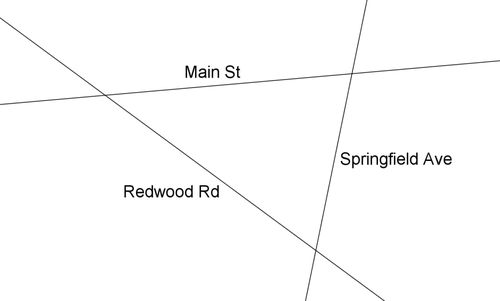
12. ¿El punto de interés es el incentro o el circuncentro?
13. Encuentra el punto en el mapa que es equidistante de cada una de las tres carreteras.
14. ¿Cómo podrías doblar el mapa en dos lugares para encontrar el punto equidistante de cada una de las tres vías?
15. Justifica la siguiente declaración: Teniendo en cuenta tres puntos no colineales, existe exactamente un círculo que pasa por los puntos.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.5.
El vocabulario
| Término | Definición |
|---|---|
| bisectriz perpendicular | Una bisectriz perpendicular de un segmento de línea pasa a través del punto medio del segmento de línea e interseca el segmento de línea en\(90^{\circ}\). |
| Círculo de un Triángulo con Inscripciones | El círculo más grande contenido dentro del triángulo. El círculo inscrito simplemente tocará cada uno de los tres lados del triángulo (es tangente a cada uno de los tres lados del triángulo). |
Recursos adicionales
Elemento Interactivo

