4.23: Medianas
- Page ID
- 107541
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Segmento de línea que une un vértice y el punto medio del lado opuesto de un triángulo.
En un triángulo, el segmento de línea que une un vértice y el punto medio del lado opuesto se denomina mediana.
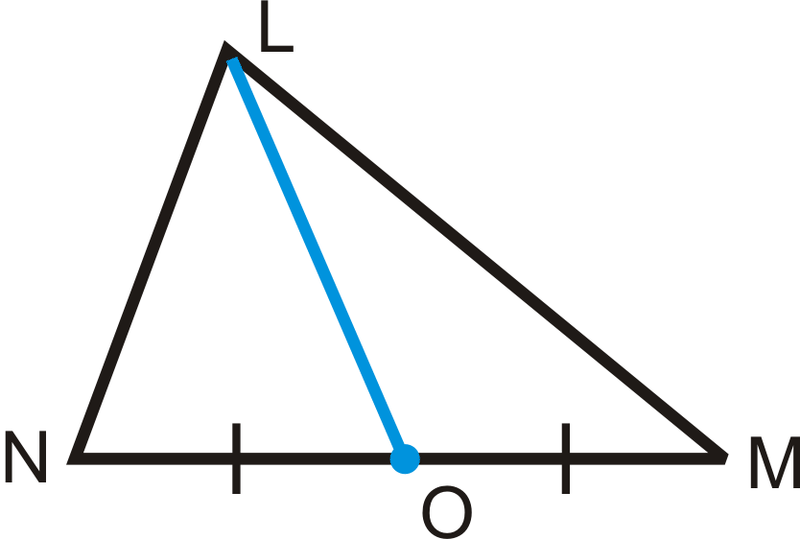
\ overline {LO}\) es la mediana de L\) al punto medio de\ overline {NM}\).
Si dibujas las tres medianas se cruzarán en un punto llamado centroide.
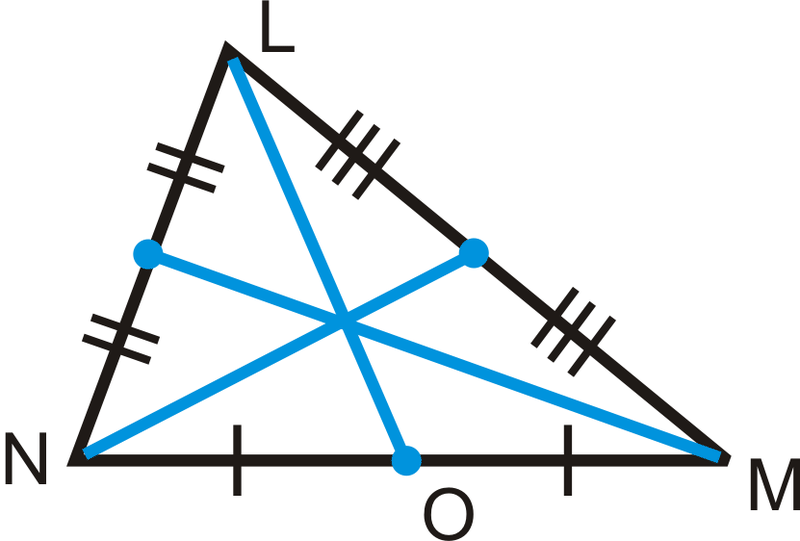
El centroide es el “punto de equilibrio” de un triángulo. Esto significa que si tuvieras que cortar el triángulo, el centroide es su centro de gravedad para poder equilibrarlo ahí.
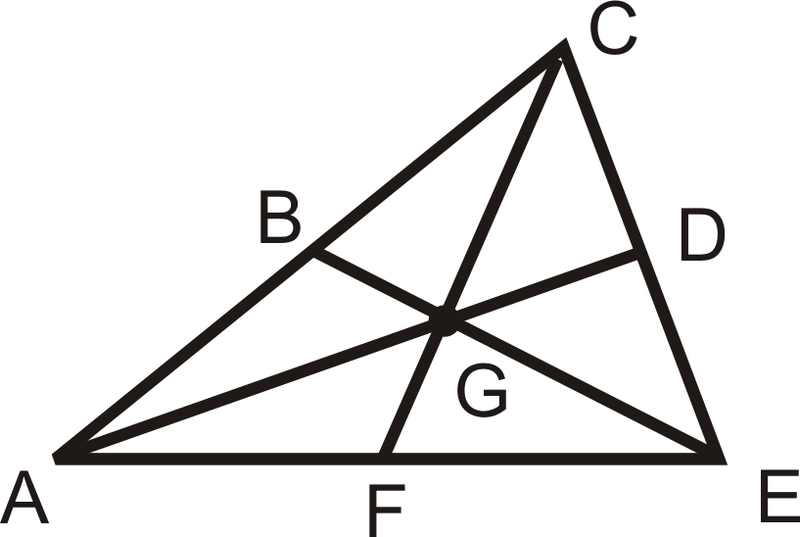
El Teorema de la Mediana establece que las medianas de un triángulo se cruzan en un punto llamado centroide que es dos tercios de la distancia desde los vértices hasta el punto medio de los lados opuestos.
Entonces si\(G\) es el centroide, entonces:
\(AG=\dfrac{2}{3} AD, CG=\dfrac{2}{3} CF,\:EG=\dfrac{2}{3} BE\)
\(DG=\dfrac{1}{3} AD, FG=\dfrac{1}{3} CF,\:BG=\dfrac{1}{3} BE\)
\(And\: by \:substitution:DG =\dfrac{1}{2} AG,\:FG=\dfrac{1}{2} CG,\:BG=\dfrac{1}{2} EG\)
Ejemplo\(\PageIndex{1}\)
\(B\),\(D\), y\(F\) son los puntos medios de cada lado y\(G\) es el centroide. Si\(CG=16\), encontrar\(GF\) y\(CF\).
Solución
Usa el Teorema de la Mediana.
\(\begin{align*} CG&=\dfrac{2}{3} CF \\ 16&=\dfrac{2}{3} CF \\ CF&=24.\end{align*}\)
Por lo tanto,\(GF=8\).
Ejemplo\(\PageIndex{2}\)
Verdadero o falso: La mediana bisecta el lado con el que se cruza.
Solución
Esta afirmación es cierta. Por definición, una mediana cruza un lado de un triángulo en su punto medio. Los puntos medios dividen los segmentos en dos partes iguales.
Ejemplo\(\PageIndex{3}\)
\(I\),\(K\), y\(M\) son puntos medios de los lados de\(\Delta HJL\).
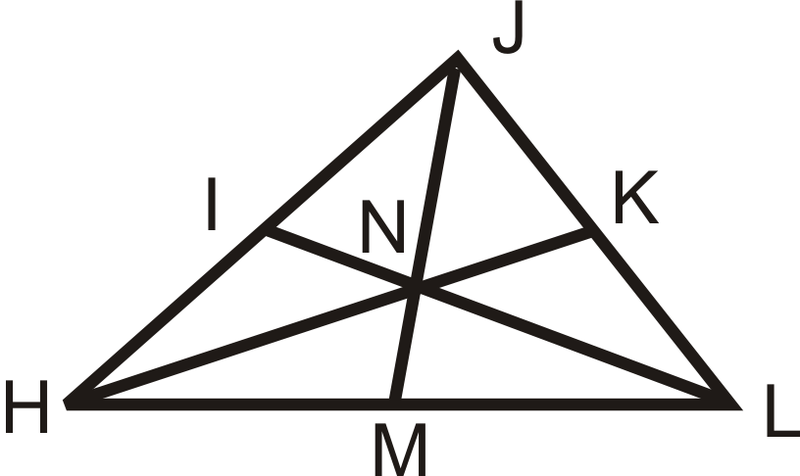
Solución
Si\(JM=18\), encontrar\(JN\) y\(NM\). Si\(HN=14\), encontrar\(NK\) y\(HK\).
Usa el Teorema de la Mediana.
\(JN=\dfrac{2}{3} \cdot 18=12. NM=JM−JN=18−12\). \(NM=6\).
\(14=\dfrac{2}{3} \cdot HK\)
\(14\cdot \dfrac{3}{2} =HK=21\). \(NK\)es un tercio de 21,\(NK=7\).
Ejemplo\(\PageIndex{4}\)
H es el centroide de\(\Delta ABC\) y\(DC=5y−16\). Encontrar\(x\) y\(y\).
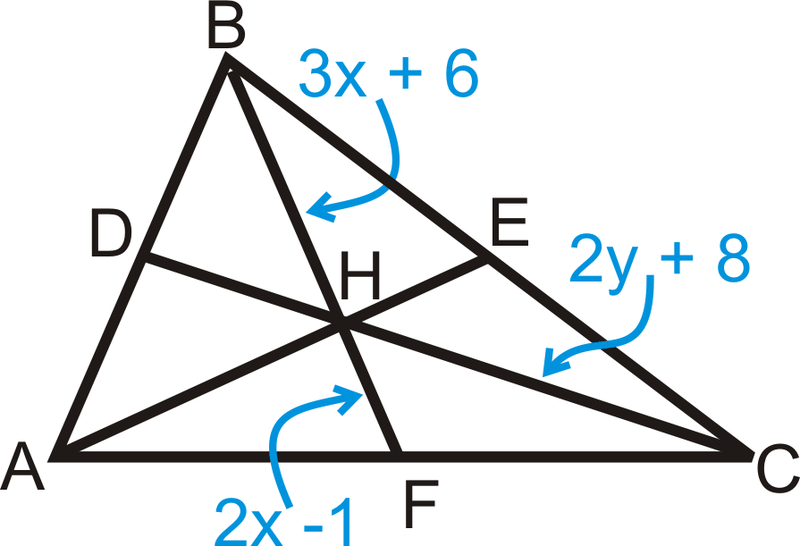
Solución
Para resolver, utilice el Teorema Mediana. Configurar y resolver ecuaciones.
\(\begin{align*} \dfrac{1}{2} BH=HF &\rightarrow BH=2HF &\qquad HC=\dfrac{2}{3} DC &\rightarrow \dfrac{3}{2} HC=DC \\ 3x+6&=2(2x−1) &\qquad \dfrac{3}{2} (2y+8)&=5y−16\\ 3x+6&=4x−2 &\qquad 3y+12 &=5y−16 \\ 8&=x &\qquad 28&=2y\rightarrow 14=y\end{align*} \)
Ejemplo\(\PageIndex{5}\)
\(B\)\(D\), y\(F\) son los puntos medios de cada lado y G es el centroide. Si\(BG=5\), encuentra\(GE\) y\(BE\)
Solución
Usa el Teorema de la Mediana.
\(\begin{align*} BG&=\dfrac{1}{3} BE \\ 5&=\dfrac{1}{3} BE \\ BE&=15.\end{align*}\)
Por lo tanto,\(GE=10\).
Revisar
Para las preguntas 1-4\(B\),\(D\),, y\(F\) son los puntos medios de cada lado y\(G\) es el centroide. Encuentra las siguientes longitudes.
- Si\(CG=16\), encuentra\(GF\) y\(CF\)
- Si\(AD=30\), encuentra\(AG\) y\(GD\)
- Si\(GF=x\), encuentra\(GC\) y\(CF\)
- Si\(AG=9x\) y\(GD=5x−1\), encontrar\(x\) y\(AD\).
Problemas de varios pasos Encuentra la ecuación de una mediana en el plano x−y\).
- Trazar\(\Delta ABC:\:A(−6,4)\),\ :B (−2,4)\)\ :y\ :C (6, −4)\)
- Encuentra el punto medio de\(\overline{AC}\). Etiquetarlo\(D\).
- Encuentra la pendiente de\(\overline{BD}\).
- Encuentra la ecuación de\(\overline{BD}\).
- Parcela\(\Delta DEF:\: D(−1,5),\:E(1,0),\:F(6,3)\)
- Encuentra el punto medio de\(\overline{EF}\). Etiquetarlo\(G\).
- Encuentra la pendiente de\(\overline{DG}\).
- Encuentra la ecuación de\\(overline{DG}\).
Determinar si la siguiente declaración es verdadera o falsa.
- El centroide es el punto de equilibrio de un triángulo.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.4.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| centroide | El centroide es el punto de intersección de las medianas en un triángulo. |
| Mediana | La mediana de un triángulo es el segmento de línea que conecta un vértice con el punto medio del lado opuesto. |
Recursos adicionales
Elemento interactivo
Video: Las medianas de un triángulo
Actividades: Medians Discusión Preguntas
Ayudas de Estudio: Bisectores, Medianos, Altitudes Guía de Estudio
Mundo real: Medianas