4.28: Fundamentos del Teorema de Pitágoras
- Page ID
- 107498
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar triples y calcular lados faltantes. Utilizar aplicaciones de medición indirecta
Derivar y Usar el Teorema de Pitágoras

El gatito de Tracy está atrapado a 2.8 metros sobre el suelo en el alféizar de la ventana de la casa de su abuela. Su abuela no está en casa así que decide rescatar a su gatito aterrorizado con la ayuda de sus amigos. Por razones de seguridad, la base de la escalera debe estar a 0.7 yardas de distancia de la casa y extenderse 1 yarda por encima del alféizar de la ventana. La escalera que ha tomado prestada es de 4 yardas de largo.
Mientras Tracy posiciona la escalera en su lugar, mira hacia arriba y se pregunta si la escalera va a ser lo suficientemente alta como para que pueda rescatar a su gatito.
En este concepto, aprenderás a derivar y utilizar el Teorema de Pitágoras.
Teorema de Pitágoras
Los triángulos a menudo se nombran de acuerdo a la medida de los ángulos que contienen. Un triángulo agudo tiene tres ángulos de tal manera que cada uno de los tres ángulos es menor que\(90^{\circ}\). Un triángulo obtuso tiene dos ángulos tales que la medida de cada uno de estos ángulos es menor que\(90^{\circ}\) y la medida del tercer ángulo es mayor que\(90^{\circ}\). Un triángulo rectángulo tiene un ángulo que tiene una medida de\(90^{\circ}\) y dos ángulos agudos de tal manera que la suma de sus medidas es igual\(90^{\circ}\). Los dos ángulos agudos de un triángulo rectángulo son complementarios, su suma es igual\(90^{\circ}\).
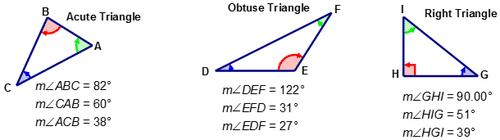
De los tres triángulos mostrados en el diagrama anterior, el triángulo rectángulo es el que más se utiliza para resolver problemas del mundo real. Este tipo de triángulo tiene características que son únicas sólo para los triángulos rectos. Cada triángulo tiene tres lados y tres ángulos. Los lados de un triángulo rectángulo tienen nombres que sólo se aplican a un triángulo rectángulo.
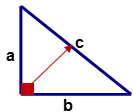
Los dos lados del triángulo rectángulo etiquetados como 'a' y 'b' se llaman las patas del triángulo. El lado del triángulo opuesto al ángulo recto (\(90^{\circ}\)) etiquetado como 'c' se llama hipotenusa y es el lado más largo del triángulo rectángulo. Los nombres de las piernas 'a' y 'b' se pueden cambiar de una pierna a la otra pero la hipotenusa 'c' debe ser el lado opuesto al ángulo recto del triángulo.
La relación entre la hipotenusa y las patas de un triángulo rectángulo se define por el Teorema de Pitágoras que establece que el cuadrado de la longitud de la hipotenusa es igual a la suma de la longitud de la pierna 'a' cuadrada y la longitud de la pierna 'b' cuadrada. El Teorema de Pitágoras es establecido por la ecuación.
\(c^2= a^2+b^2\)
La ecuación que representa el Teorema de Pitágoras contiene tres piezas que son a, b y c. Si conoces dos de estas piezas, entonces la ecuación puede ser utilizada para calcular la tercera pieza. El Teorema de Pitágoras también se puede utilizar para determinar si un triángulo dado es efectivamente un triángulo rectángulo.
Mira el triángulo que se da a continuación. No hay ningún ángulo recto marcado para indicar que el triángulo es un triángulo rectángulo. ¿El triángulo es un triángulo rectángulo? El Teorema de Pitágoras puede ser utilizado para responder a esta pregunta.
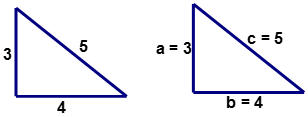
\(c^2=a^2+b^2\)
Primero, rellene los valores para las letras\(a\),\(b\) y\(c\).
\(\begin{align*}c^2&=a^2+b^2 \\ (5)^2&=(3)^2+(4)^2\end{align*}\)
A continuación, realice las operaciones indicadas en ambos lados de la ecuación.
\(\begin{align*}(5)^2&=(3)^2+(4)^2 \\ (5\times 5)&=(3\times 3)+(4\times 4) \\ 25&=9+16\end{align*}\)
Después, simplifique la ecuación sumando los valores en el lado derecho de la ecuación.
\(\begin{align*}25&=9+16 \\ 25&=25\end{align*}\)
Ambos lados de la ecuación son iguales. Los valores de (3, 4 y 5) dieron como resultado que\ (c^2=a^2+b^2 sea una verdadera declaración de igualdad. Por lo tanto, el triángulo dado es un triángulo rectángulo.
Los valores de (3, 4 y 5) para los enteros positivos (a, b, c) respectivamente, son una combinación de números conocidos como Triple Pitágoras que son un conjunto de tres números enteros que satisfacen el Teorema de Pitágoras\(c^2=a^2+b^2\). Otras Triples Pitágoras se pueden generar multiplicando los valores de cualquier Triple Pitagórica conocida por cualquier entero positivo. Si los valores (3, 4 y 5) se multiplican por 2, entonces se crea otro Triple pitagórico (6, 8 y 10). Si los valores (6, 8 y 10) se multiplican por 4 entonces se genera otro Triple pitagórico (24, 32 y 40).
Los valores recién generados han sido sustituidos en el Teorema de Pitágoras\(c^2=a^2+b^2\),, para asegurar que son Triples Pitágoras.
\(\begin{align*} c^2&=a^2+b^2 &\qquad c^2&=a^2+b^2 \\ (10)^2&=(6)^2+(8)^2 &\qquad (40)^2&=(24)^2+(32)^2 \\ (10\times 10)&=(6\times 6)+(8\times 8)&\qquad (40\times 40)&=(24\times 24)+(32\times 32) \\ 100&=36+64&\qquad 1600&=576+1024 \\ 100&=100 &\qquad 1600&=1600\end{align*}\)
Cada una de las nuevas Triples Pitágoras han resultado en\(c^2=a^2+b^2\) ser una verdadera declaración de igualdad.
Si sabes que un triángulo dado es un triángulo rectángulo, entonces el Teorema de Pitágoras se puede utilizar para calcular la longitud de un lado desconocido del triángulo cuando conoces las longitudes de dos de los lados.
Veamos un ejemplo.
Para el siguiente triángulo rectángulo, calcule la longitud del lado desconocido '\(b\)?'
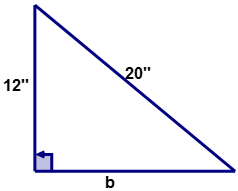
Primero, usa el Teorema de Pitágoras para calcular la longitud del lado '\(b\).'
\(c^2= a^2+b^2\)
A continuación, rellene los valores dados para los lados\(a\) '' y lado '\(c\).'
\(\begin{align*}c^2&=a^2+b^2 \\ (20)^2&=(12)^2+b^2\end{align*}\)
A continuación, realizar las operaciones indicadas.
\(\begin{align*}(20)^2&=(12)^2+b^2 \\ (20\times 20)&=(12\times 12)+b^2 \\ 400&=144+b^2\end{align*}\)
A continuación, resta 144 de ambos lados de la ecuación para aislar la variable y simplificar ambos lados de la ecuación.
\(\begin{align*}400&=144+b^2 \\ 400−144&=144−144+b^2 \\ 256&=b^2\end{align*}\)
Entonces, resuelve para 'b' tomando la raíz cuadrada de ambos lados de la ecuación. Recuerde que tomar la raíz cuadrada es la operación inversa de cuadratura.
\(\begin{align*}256&=b^2 \\ \sqrt{256}&=\sqrt{b^2} \\ 16&=b\end{align*}\)
La respuesta es 16.
La longitud del lado '\(b\)' es de 16 pulgadas.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Tracy y su misión de rescate. Necesita saber si la escalera que está usando es lo suficientemente larga como para rescatar a su gatito.
Solución
Primero, dibuje y etiquete una imagen para modelar el problema.
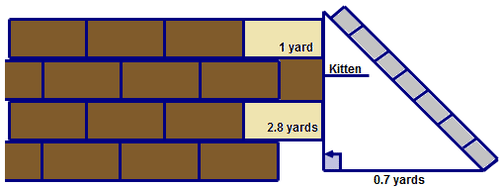
A continuación, mire el triángulo rectángulo y determine las medidas de los dos lados conocidos.
\(a=3.8\:yards\)
\(b=0.7\:yards\)
A continuación, utilice el Teorema de Pitágoras para calcular la longitud de la escalera que es la hipotenusa del triángulo rectángulo.
\(c^2= a^2+b^2\)
Primero, rellene los valores para 'a' y 'b'.
\(\begin{align*}c^2&=a^2+b^2 \\ c^2&=(3.8)^2+(0.7)^2\end{align*}\)
A continuación, realice las operaciones indicadas y simplifique la ecuación.
\(\begin{align*}c^2&=(3.8\times 3.8)+(0.7\times 0.7) \\ c^2&=14.44+0.49 \\ c^2&=14.93\:yards\end{align*}\)
Entonces, resuelve para 'c' tomando la raíz cuadrada de cada lado de la ecuación.
\(\begin{align*}c^2&=14.93 \\ \sqrt{c^2}&=\sqrt{14.93} \\ c&=3.86\end{align*}\)
La respuesta es 3.86.
La escalera debe tener 3.86 yardas de largo para rescatar al gatito. La escalera que Tracy está usando es lo suficientemente larga.
Ejemplo\(\PageIndex{2}\)
Usa el Teorema de Pitágoras para calcular la longitud del lado faltante del siguiente triángulo rectángulo:
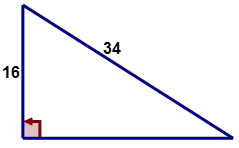
Solución
Primero, ¿determinar qué representan los valores dados y qué lado falta?
\(\begin{align*} a&=16 \\ b&=? \\ c&=34\end{align*}\)
A continuación, sustituya los valores dados en una ecuación que represente el Teorema de Pitágoras.
\(\begin{align*}c^2&=a^2+b^2 \\ (34)^2&=(16)^2+b^2\end{align*}\)
A continuación, realice las operaciones indicadas en ambos lados de la ecuación.
\(\begin{align*}(34)^2&=(16)^2+b^2 \\ (34\times 34)&=(16\times 16)+b^2 \\ 1156&=256+b^2\end{align*}\)
A continuación, resta 256 de ambos lados de la ecuación para aislar la variable.
\(\begin{align*}1156&=256+b^2 \\ 1156−256&=256−256+b^2\end{align*}\)
A continuación, simplifique la ecuación.
\(\begin{align*}1156−256&=256−256+b^2 \\ 900&=b^2\end{align*} \)
Después, tomar la raíz cuadrada de ambos lados de la ecuación para resolver para la variable '\(b\).'
\(\begin{align*} 900&=b^2 \\ \sqrt{900}&=\sqrt{b^2} \\ 30&=b\end{align*}\)
La respuesta es\(b=30\).
Ejemplo\(\PageIndex{3}\)
Encuentra la longitud de la hipotenusa de un triángulo rectángulo dado que las longitudes de las patas\(a\) '' y “\(b\)'son 14 y 48 centímetros, respectivamente.
Solución
Primero, dibuje y etiquete un triángulo rectángulo para representar la información dada.
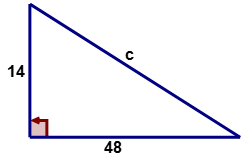
A continuación, sustituya los valores dados en una ecuación que represente el Teorema de Pitágoras.
\(\begin{align*} c^2&= a^2+b^2 \\ c^2&= (14)^2+(48)^2\end{align*}\)
A continuación, realice las operaciones indicadas y simplifique la ecuación.
\(\begin{align*} c^2= (14)^2+(48)^2 \\ c^2&= (14\times 14)+(48\times 48) \\ c^2&= 196+2304\end{align*} \)
A continuación, simplifique la ecuación sumando los valores en el lado derecho de la ecuación.
\(\begin{align*} c^2&= 196+2304 \\ c^2&= 2500\end{align*}\)
Después, tomar la raíz cuadrada de ambos lados de la ecuación para resolver para la variable '\(c\).'
\(\begin{align*} c^2&= 2500 \\ \sqrt{c^2}&=2500 \\ c&=50\end{align*}\)
La respuesta es\(c=50\).
La longitud de la hipotenusa es de 50 cm.
Ejemplo\(\PageIndex{4}\)
Si '\(a\)' y '\(b\)' son valores tales que\(a,\:b\in N\) y\(a>b\) luego los lados de un triángulo rectángulo son\(a^2+b^2\),\(a^2−b^2\), y\(2ab\) como se muestra en el diagrama de abajo.
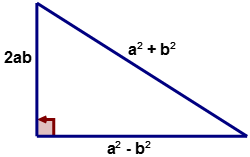
Solución
Completa la siguiente tabla para generar Triples pitagóricos.
| \ (av | \( b\) | \(a^2−b^2\) | \(2ab\) | \(a^2+b^2\) |
| 4 | 2 | 12 | 16 | 20 |
| 5 | 3 | 16 | 30 | 34 |
| 6 | 4 | 20 | 48 | 52 |
Primero, usando\(a=4 and \(b=2\) evaluar\(a^2−b^2\) sustituyendo los valores dados en la expresión.
\(\begin{align*} &a^2−b^2 \\ &(4)^2−(2)^2\end{align*}\)
A continuación, realizar las operaciones indicadas y simplemente la expresión.
\(\begin{align*} &(4)^2−(2)^2 \\ &(4\times 4)−(2\times 2) \\ &16−4 \\ &12\end{align*} \)
La respuesta es 12.
Después, coloca la respuesta en la tabla en la columna correcta.
Ahora, complete la\(a^2−b^2\) columna para los valores restantes dados de '\(a\)' y '\(b\).'
Primero, usar\(a=5\) y\(b=3\) evaluar\(a^2−b^2\) sustituyendo los valores dados en la expresión.
\(\begin{align*} &a^2−b^2 \\ &(5)^2−(3)^2\end{align*} \)
A continuación, realizar las operaciones indicadas y simplemente la expresión.
\(\begin{align*} (5)^2−(3)^2 \\ (5\times 5)−(3\times 3) \\ 25−9=16\end{align*} \)
La respuesta es 16.
Después, coloca la respuesta en la tabla en la columna correcta.
Primero, usar\(a=6\) y\(b=4\) evaluar\(a^2−b^2\) sustituyendo los valores dados en la expresión.
\(\begin{align*} &a^2−b^2 \\ &(6)^2−(4)^2 \end{align*}\)
A continuación, realizar las operaciones indicadas y simplemente la expresión.
\(\begin{align*} (6)^2−(4)^2 \\ &(6\times 6)−(4\times 4) \\ &36−16 \\ &20 \end{align*} \)
La respuesta es 20.
Después, coloca la respuesta en la tabla en la columna correcta.
Primero, usar\(a=4\) y\(b=2\) evaluar\(2ab\) sustituyendo los valores dados en la expresión.
\(2ab\)
\(2(4)(2)\)
A continuación, realizar las operaciones indicadas.
\(2(4)(2)\)
\(8(2)\)
\(16\)
La respuesta es 16.
Después, coloca la respuesta en la tabla en la columna correcta.
Ahora, complete la\(2ab\) columna para los valores restantes dados de '\(a\)' y '\(b\).'
Primero, usar\(a=5\) y\(b=3\) evaluar\(2ab\) sustituyendo los valores dados en la expresión.
\(\begin{align*} &2ab \\ &2(5)(3)\end{align*}\)
A continuación, realizar las operaciones indicadas.
\(\begin{align*} &2(5)(3) \\ &10(3) \\ &30\end{align*}\)
La respuesta es 30.
Después, coloca la respuesta en la tabla en la columna correcta.
Primero, usar\(a=6\) y\(b=4\) evaluar\(2ab\) sustituyendo los valores dados en la expresión.
\(\begin{align*} &2ab \\ &2(6)(4)\end{align*}\)
A continuación, realizar las operaciones indicadas.
\(\begin{align*}&2(6)(4) \\ &12(4) \\ &48\end{align*}\)
La respuesta es 48.
Después, coloca la respuesta en la tabla en la columna correcta.
Primero, usar\(a=4\) y\(b=2\) evaluar\(a^2+b^2\) sustituyendo los valores dados en la expresión.
\(\begin{align*} &a^2+b^2 \\ &(4)^2(2)^2\end{align*} \)
A continuación, realizar las operaciones indicadas y simplemente la expresión.
\(\begin{align*} &(4)^2+(2)^2 \\ &(4\times 4)+(2\times 2)16+4 \\ &20\end{align*}\)
La respuesta es 20.
Después, coloca la respuesta en la tabla en la columna correcta.
Ahora, complete la\(a^2+b^2\) columna para los valores restantes dados de '\(a\)' y '\(b\).'
Primero, usar\(a=5\) y\(b=3\) evaluar\(a^2+b^2\) sustituyendo los valores dados en la expresión.
\(\begin{align*} &a^2+b^2 \\ &(5)^2+(3)^2\end{align*}\)
A continuación, realizar las operaciones indicadas y simplemente la expresión.
\( \begin{align*} &(5)^2+(3)^2 \\ &(5\times 5)+(3\times 3) \\ &25+9 \\ &34 \end{align*}\)
La respuesta es 34.
Después, coloca la respuesta en la tabla en la columna correcta.
Primero, usar\(a=6\) y\(b=4\) evaluar\(a^2+b^2\) sustituyendo los valores dados en la expresión.
\(a^2+b^2\)
\((6)^2+(4)^2\)
A continuación, realizar las operaciones indicadas y simplemente la expresión.
\(\begin{align*} &(6)^2+(4)^2 \\ &(6\times 6)+(4\times 4) \\ &36+16 \\ &52\end{align*}\)
La respuesta es 52.
Después, coloca la respuesta en la tabla en la columna correcta.
Ejemplo\(\PageIndex{5}\)
Usa el Teorema de Pitágoras para encontrar la longitud de la pata faltante del siguiente triángulo rectángulo.
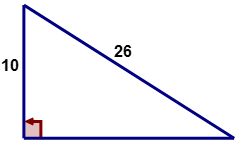
Solución
Primero, ¿determinar qué representan los valores dados y qué lado falta?
\(\begin{align*} a&=? \\ b&=10 \\ c&=26\end{align*} \)
A continuación, sustituya los valores dados en una ecuación que represente el Teorema de Pitágoras.
\(\begin{align*} c^2&=a^2+b^2 \\ (26)^2&=a^2+(10)^2\end{align*}\)
A continuación, realice las operaciones indicadas y simplifique la ecuación.
\(\begin{align*} (26)^2&=a^2+(10)^2 \\ (26\times 26)&=a^2+(10\times 10) \\ 676&=a^2+100\end{align*}\)
A continuación, resta 100 de ambos lados de la ecuación para aislar la variable.
\(\begin{align*} 676&=a^2+100 \\ 676−100&=a^2+100−100 \end{align*} \)
A continuación, simplifique la ecuación.
\(\begin{align*} 676−100&=a^2+100−100 \\ 576&=a^2\end{align*}\)
Después, tomar la raíz cuadrada de ambos lados de la ecuación para resolver para la variable 'a'.
\(\begin{align*}576&=a^2 \\ \sqrt{576}&=\sqrt{a^2} \\ 24&a\end{align*}\)
La respuesta es\(a=24\).
Revisar
Usa el Teorema de Pitágoras para encontrar las dimensiones que faltan de cada triángulo rectángulo.
- \(a=3,\:b=4,\:c=?\)
- \(a=6,\:b=8,\:c=?\)
- \(a=9,\:b=12,\:c=?\)
- \(a=27,\:b=36,\:c=?\)
- \(a=15,\:b=20,\:c=?\)
- \(a=18,\:b=24,\:c=?\)
- \(a=?,\:b=16,\:c=20\)
- \(a=?,\:b=28,\:c=35\)
- \(a=30,\:b=?,\:c=50\)
- \(a=33,\:b=?,\:c=55\)
- \(a=1.5,\:b=?,\:c=2.5\)
- \(a=36,\:b=?,\:c=60\)
Indique si las siguientes afirmaciones son Verdadero o Falso.
- El Teorema de Pitágoras funcionará para cualquier triángulo.
- El lado más largo de un triángulo rectángulo se llama hipotenusa.
- Un Triple pitagórico solo se puede encontrar en un triángulo rectángulo.
vocabulario
| Término | Definición |
|---|---|
| Hipotenusa | La hipotenusa de un triángulo rectángulo es el lado más largo del triángulo rectángulo. Está frente al ángulo recto. |
| Patas de un Triángulo Recto | Las patas de un triángulo rectángulo son los dos lados más cortos del triángulo rectángulo. Las patas están adyacentes al ángulo recto. |
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
| Triple Pitágoras | Un Triple Pitágoras es un conjunto de tres números enteros a, b y c que satisfacen el Teorema de Pitágoras,\(a^2+b^2=c^2\). |
| Triángulo Recto | Un triángulo rectángulo es un triángulo con un ángulo de 90 grados. |
Recursos adicionales
Vídeo: Teorema de Pitágoras 2
Práctica: Fundamentos del teorema de Pitágoras
Mundo real: Medir el mundo

