4.39: La fórmula de distancia y álgebra
- Page ID
- 107482
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usando el Teorema de Pitágoras para determinar distancias
Supongamos que usted y su amigo estaban en una búsqueda del tesoro. Comenzando desde el mismo lugar, caminaste 5 cuadras al este y 3 cuadras al norte. Tu amigo caminó 7 cuadras al oeste y 2 cuadras al sur. Si cada cuadra tuviera una décima de milla de largo, ¿podrías calcular qué tan lejos estaban tú y tu amigo? ¿Cómo lo harías?
La fórmula de distancia
Para entender la fórmula de distancia, primero veremos el siguiente problema:
Encuentra la longitud del segmento que conecta\((1, 5)\) y\((5, 2)\).
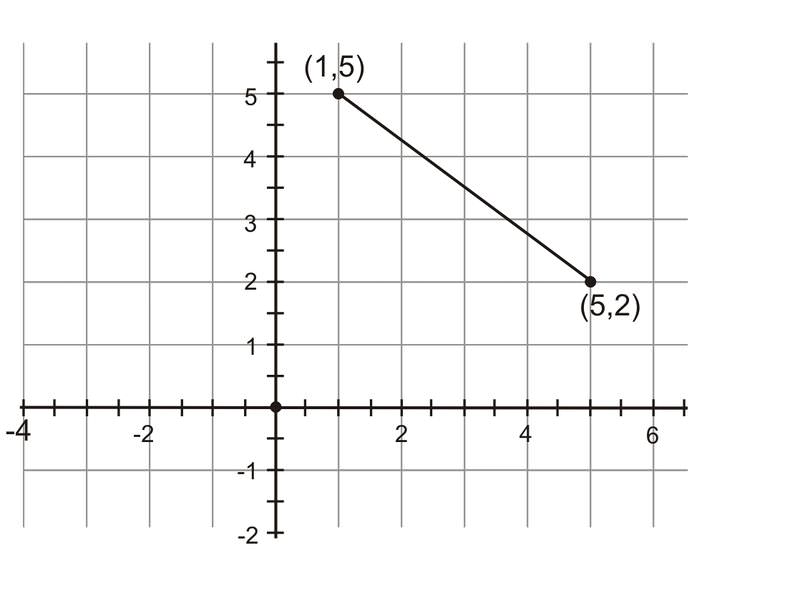
La pregunta le pide identificar la longitud del segmento. Debido a que el segmento no es paralelo a ninguno de los ejes, es difícil de medir dada la cuadrícula de coordenadas.
Sin embargo, es posible pensar en este segmento como la hipotenusa de un triángulo rectángulo. Dibuja una línea vertical y una línea horizontal. Encuentra el punto de intersección. Este punto representa el tercer vértice en el triángulo rectángulo.
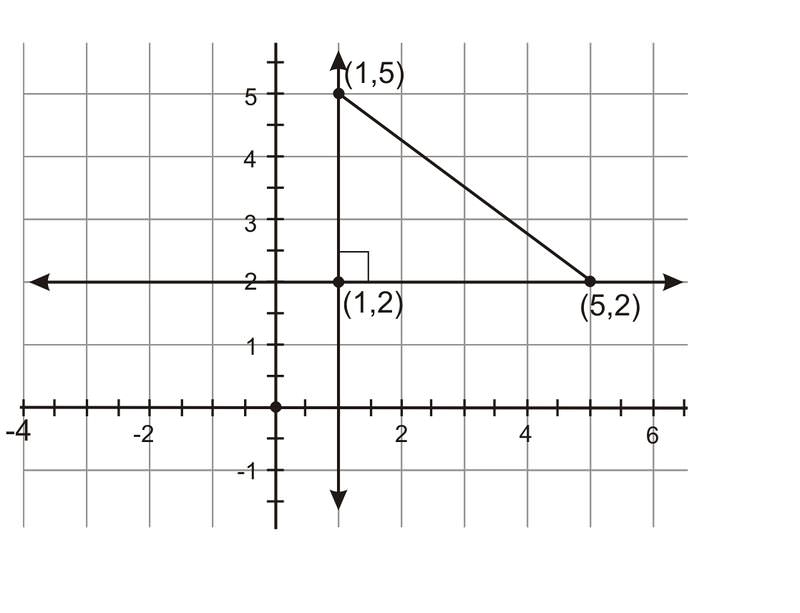
Puedes contar fácilmente las longitudes de las patas de este triángulo en la cuadrícula. La pata vertical se extiende de\((1, 2)\) a\((1, 5)\), por lo que es\(\mid5−2\mid=\mid3\mid=3\: units\) larga. La pata horizontal se extiende de\((1, 2)\) a\((5, 2)\), por lo que es\(\mid5−1\mid=\mid4\mid=4\: units\) larga. Usa el Teorema de Pitágoras con estos valores para las longitudes de cada pierna para encontrar la longitud de la hipotenusa.
\(\begin{aligned} a^2+b^2 & =c^2 \\ 3^2+4^2 & =c^2 \\ 9+16 & =c^2 \\ 25 & =c^2 \\ \sqrt{25} & =\sqrt{c^2} \\ 5 & = c\end{aligned}\)
El segmento de conexión\((1, 5)\) y\((5, 2)\) es de 5 unidades de largo.
Los matemáticos han simplificado este proceso y creado una fórmula que utiliza estos pasos para encontrar la distancia entre dos puntos cualesquiera en el plano de coordenadas. Si usas la fórmula de distancia, no tienes que dibujar las líneas extra.
La fórmula de distancia establece: Puntos dados\((x_1,y_1)\) y\((x_2,y_2)\), la longitud del segmento que conecta esos dos puntos es\(d=\sqrt{\left(y_{2}-y_{1}\right)^{2}+\left(x_{2}-x_{1}\right)^{2}}\).
Usemos la fórmula de distancia para completar los siguientes problemas:
- Encuentra la distancia entre\((–3, 5)\) y\((4, –2)\).
Usa la fórmula de distancia. Dejar\((x_1,y_1)=(−3,5)\) y\((x_2,y_2)=(4,−2)\).
\ (\ begin {array} {l}
d=\ sqrt {(-2-5) ^ {2} + (4- (-3)) ^ {2}}\ fila derecha\ sqrt {(-7) ^ {2} +7^ {2}}\
d=\ sqrt {98} =7\ sqrt {2}\ text {unidades}
\ end {array}\)
- Un día a las 8 de la mañana, Amir decide caminar en línea recta por la playa. Después de dos horas de no hacer giros y viajar a un ritmo constante, Amir estaba a dos millas al este y cuatro millas al norte de su punto de partida. ¿Qué tan lejos caminó Amir y cuál era su velocidad de caminar?
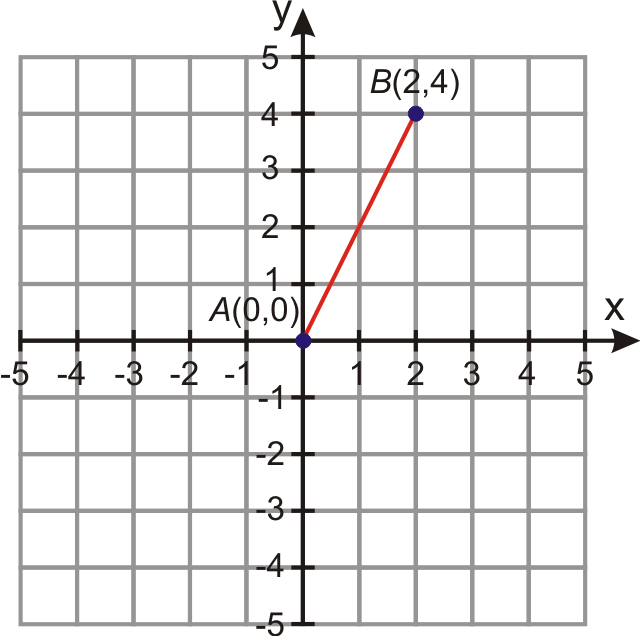
Trazar la ruta de Amir en una gráfica de coordenadas. Podemos situar su punto de partida en el origen,\(A=(0,0)\). Entonces, su punto final será en ese punto\(B=(2,4)\). La distancia se puede encontrar con la fórmula de distancia.
\(\begin{aligned} d&=\sqrt{(4−0)^2+(2−0)^2}=\sqrt{(4)^2+(2)^2}=\sqrt{16+4}=\sqrt{20} \\ d &=4.47\text { miles } \end{aligned} \).
Desde que Amir caminó 4.47 millas en 2 horas, su velocidad es:
\(Speed=\dfrac{4.47 \text{ miles }}{2 \text{ hours }}=2.24 \: mi/h\)
Ejemplo\(\PageIndex{1}\)
Antes, te dijeron que en una búsqueda del tesoro, comenzando desde el mismo lugar, caminabas 5 cuadras al este y 3 cuadras al norte y tu amigo caminaba 7 cuadras al oeste y 2 cuadras al sur. Cada cuadra tiene una décima de milla de largo. ¿Qué tan lejos estaban tú y tu amigo?
Solución
Puede ser útil dibujar una gráfica para visualizar la situación. Suponiendo que el punto de partida estaba en (0,0) y la distancia entre cada punto es igual a una cuadra, si caminabas 5 cuadras al este y 3 cuadras al norte, tus coordenadas serían\((-5, 3)\). Tu amigo caminó 7 cuadras al oeste y 2 cuadras al sur, por lo que sus coordenadas serían\((7,-2)\)
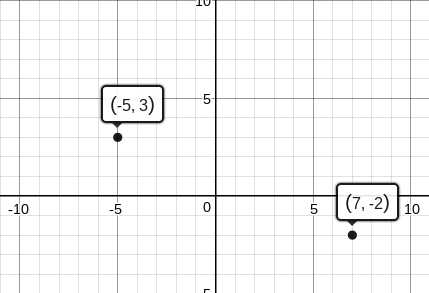
Ahora, puedes calcular la distancia entre estos dos puntos usando la fórmula de distancia. Todo lo que necesitas hacer es conectar los puntos a la fórmula y resolver.
\ (\ begin {alineado} d&=\ sqrt {\ izquierda (y_ {2} -y_ {1}\ derecha) ^ {2} +\ izquierda (x_ {2} -x_ {1}\ derecha) ^ {2}}\\
d&=\ sqrt {(−2−3) ^2+ (7− (−5)) ^2}\ fila derecha\ sqrt {(−5) ^2+12^2}\\
d&=\ sqrt {169} =13\ final {alineado}\)
Tú y tu amigo están a 13 unidades el uno del otro. Dado que cada bloque tiene una décima de milla de largo, puedes multiplicar 13 por una décima para obtener la distancia real.
\(13 \times \dfrac{1}{10}=\dfrac{13}{10}=1.3\)
Tú y tu amigo están a 1.3 millas el uno del otro.
Ejemplo\(\PageIndex{2}\)
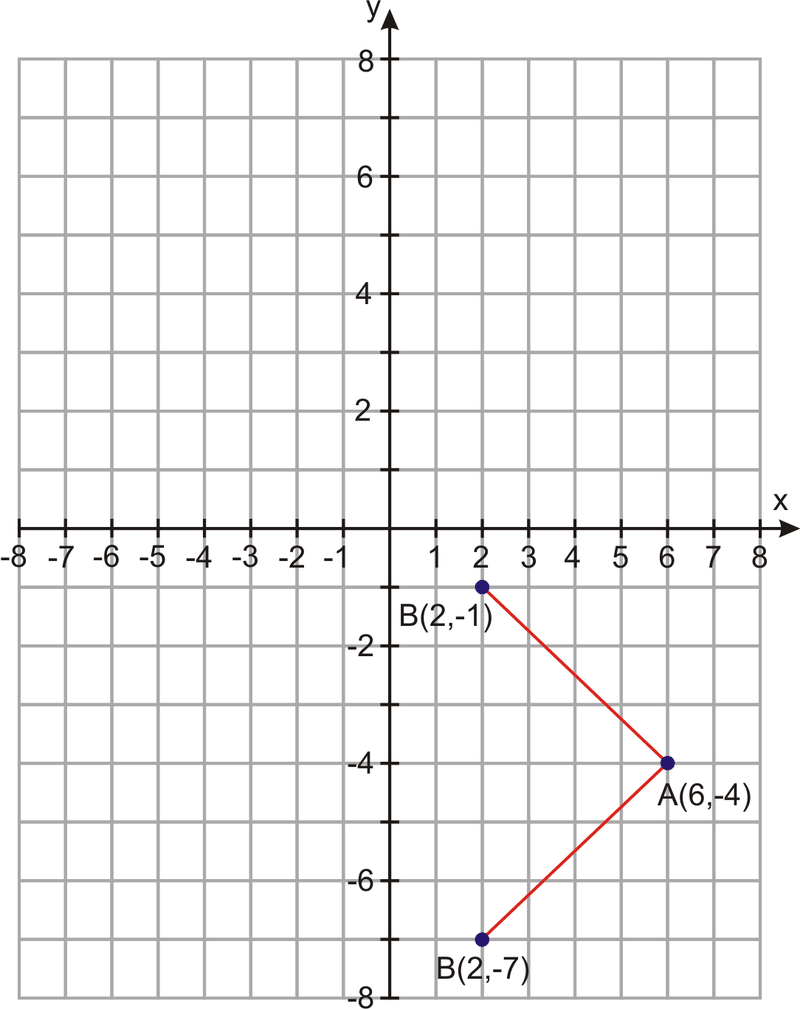
Punto\(A=(6,−4)\) y punto\(B=(2,k)\). ¿Cuál es el valor de\(k\) tal que la distancia entre los dos puntos sea 5?
Solución
Usa la fórmula de distancia.
\(d=\sqrt{(y_1−y_2)^2+(x_1−x_2)^2}\Rightarrow 5=\sqrt{(4−k)^2+(6−2)^2}\)
\ (\ begin {alineado} Cuadrado\: ambos\ :lados\ :de\ :la ecuación\:. &\ qquad& 5^2&= [\ sqrt {(4−k) ^2+ (6−2) ^2}] ^2\\
Simplificar. &\ qquad& 25&= (−4−k) ^2+16\\ Elimina\: los\ :paréntesis. &\ qquad& 0&=k^2+8k+16−9\\
Simplificar. &\ qquad& 0&=k^2+8k+7\\
Encuentra\ :k\ :usando\ :la fórmula\ :cuadrática\:. &\ qquad& k&=\ dfrac {−8\ pm\ sqrt {64−28}} {2} =\ dfrac {−8\ pm\ sqrt {36}} {2} =\ dfrac {−8\ pm6} {2}\ end {alineado}\)
\(k=−7\)o\(k=−1\). Hay dos posibilidades para el valor de k. Vamos a graficar los puntos para obtener una representación visual de nuestros resultados.
Revisar
En 1—10, encuentra la distancia entre los dos puntos.
- \((x_1,y_1)\)y\((x_2,y_2)\)
- \((7, 7)\)y\((–7, 7)\)
- \((–3, 6)\)y\((3, –6)\)
- \((–3, –1)\)y\((–5, –8)\)
- \((3, –4)\)y\((6, 0)\)
- \((–1, 0)\)y\((4, 2)\)
- \((–3, 2)\)y\((6, 2)\)
- \((0.5, –2.5)\)y\((4, –4)\)
- \((12, –10)\)y\((0, –6)\)
- \((2.3, 4.5)\)y\((–3.4, –5.2)\)
- Encuentra todos los puntos que tengan una coordenada x de —4 y cuya distancia desde el punto\((4, 2)\) sea 10.
- Encuentra todos los puntos que tengan una coordenada y de 3 y cuya distancia desde el punto\((–2, 5)\) sea 8.
- Michelle decide andar en bicicleta algún día. Primero monta su bicicleta hacia el sur por 12 millas, y luego cambia la dirección del sendero para bicicletas y viaja en la nueva dirección por un tiempo más. Cuando se detiene, Michelle está a 2 millas al sur y 10 millas al oeste de su punto de partida. Encuentra la distancia total que Michelle recorrió desde su punto de partida.
Reseña Mixta
- Resolver\((x−4)^2=121\).
- ¿Cuál es el\(GCF\) de\(21ab^4\) y\(15a^7b^2\)?
- Evaluar\(_10C_7\) y explicar su significado.
- Factor\(6x^2+17x+5\).
- Encuentra el área de un rectángulo con una longitud de\((16+2m)\) y un ancho de\((12+2m)\).
- Factor\(x^2−81\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.7.
El vocabulario
| Término | Definición |
|---|---|
| Fórmula de distancia | La distancia entre dos puntos\) (x_1, y_1)\) y\) (x_2, y_2)\) se puede definir como\) d=\ sqrt {(x_2−x_1) ^2+ (y_2−y_1) ^2}\). |
| Fórmula de punto medio | La fórmula del punto medio dice que para los puntos finales\((x_1,y_1)\) y\((x_2,y_2)\), el punto medio es\((\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2})\). |
Recursos adicionales
Elemento Interactivo
Video: Fórmula de distancia
Actividades: Preguntas de discusión de fórmula a distancia
Práctica: La fórmula a distancia y álgebra
Mundo real: Mapa SF - Pyththm

