5.10: Área de un Paralelogramo
- Page ID
- 107510
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\(A=bh\)Úselo para encontrar área.
Un paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos.
Para encontrar el área de un paralelogramo, conviértalo en un rectángulo.
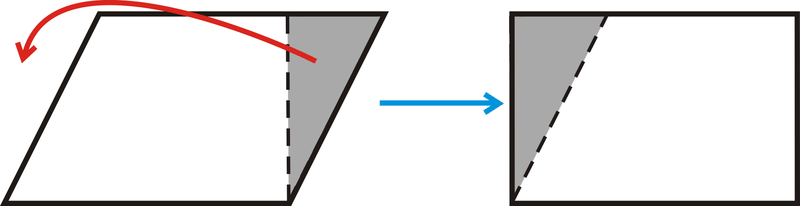
A partir de esto, vemos que el área de un paralelogramo es la misma que el área de un rectángulo. El área de un paralelogramo es\(A=bh\). La altura de un paralelogramo es siempre perpendicular a la base. Esto quiere decir que los lados no son la altura.
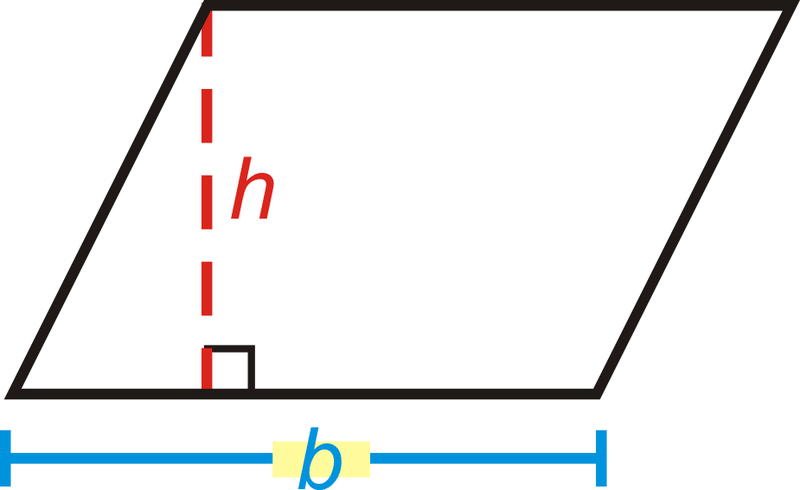
¿Y si te dieran un paralelogramo y el tamaño de su base y altura? ¿Cómo podrías encontrar la cantidad de espacio que ocupa el paralelogramo?
Ejemplo\(\PageIndex{1}\)
Encuentra el área del paralelogramo.
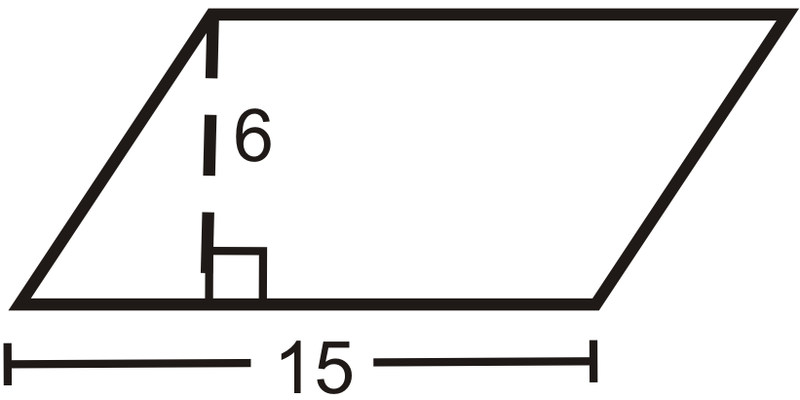
Solución
El área es\(15(6)=90\text{ un}^2\).
Ejemplo\(\PageIndex{2}\)
Encuentra el área del paralelogramo con una base de 10 m y una altura de 12 m.
Solución
El área es 10 (12) =120\ text {m} ^2\).
Ejemplo\(\PageIndex{3}\)
Encuentra el área del paralelogramo.
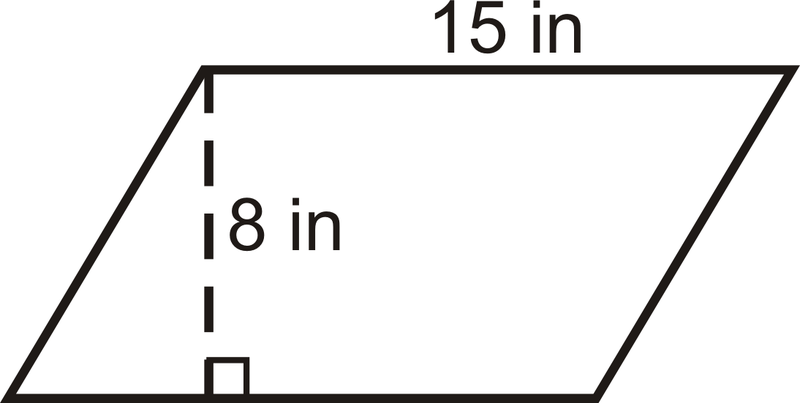
Solución
\(A=15\cdot 8=120 \text{ in}^2\)
Ejemplo\(\PageIndex{4}\)
Si el área de un paralelogramo es\(56 \text{ units }^2\) y la base es de 4 unidades, ¿cuál es la altura?
Solución
Resuelve para la altura en\(A=bh\).
\(56\text{ units }=4h\)
\(14 \text{ units }=h\)
Ejemplo\(\PageIndex{5}\)
Si la altura de un paralelogramo es de 12 m y el área es\(60 m^2\), ¿qué tan amplia es la base?
Solución
Resuelve para la base en\(A=bh\).
\(60 \text{ units } =12b\)
\(5 \text{ units } =b\)
Revisar
- Encuentra el área de un paralelogramo con altura de 20 m y base de 18 m.
- Encuentra el área de un paralelogramo con altura de 12 m y base de 15 m.
- Encuentra el área de un paralelogramo con altura de 40 m y base de 33 m.
- Encuentra el área de un paralelogramo con altura de 32 m y base de 21 m.
- Encuentra el área de un paralelogramo con altura de 25 m y base de 10 m.
Encuentra el área del paralelogramo.
-
Figura\(\PageIndex{6}\) -
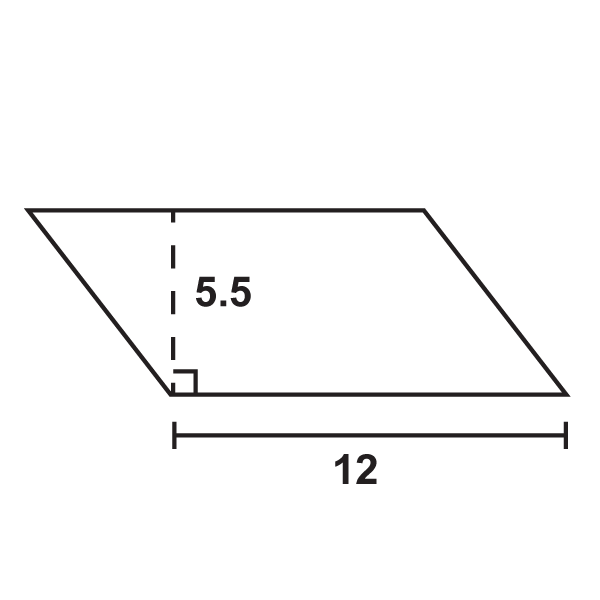
Figura\(\PageIndex{7}\) -
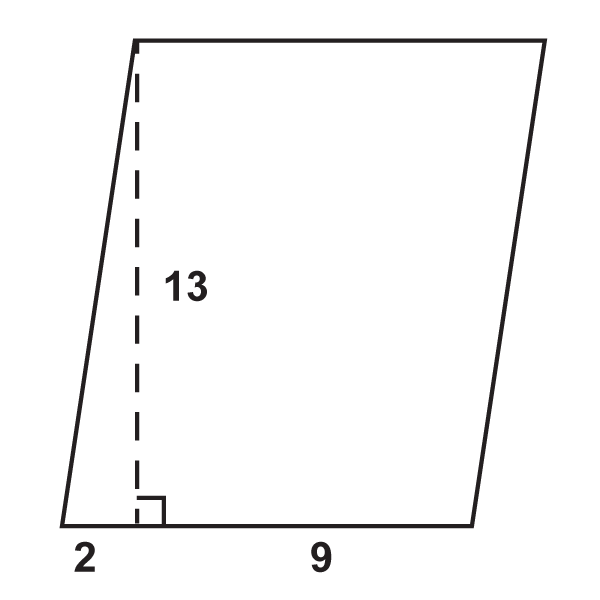
Figura\(\PageIndex{8}\) -
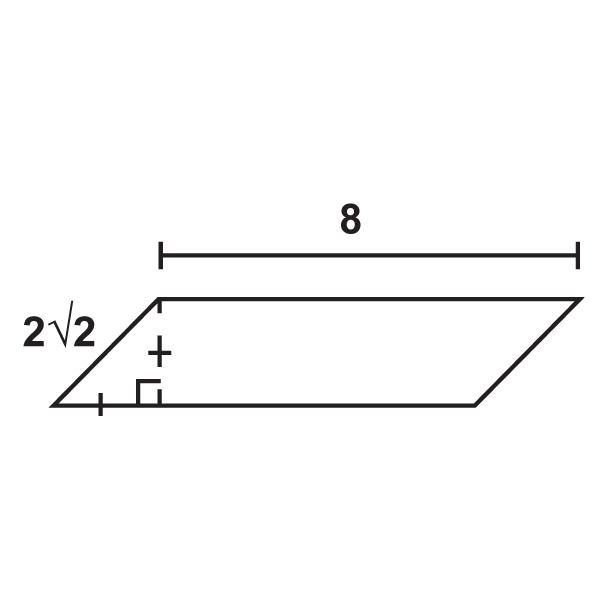
Figura\(\PageIndex{9}\) -
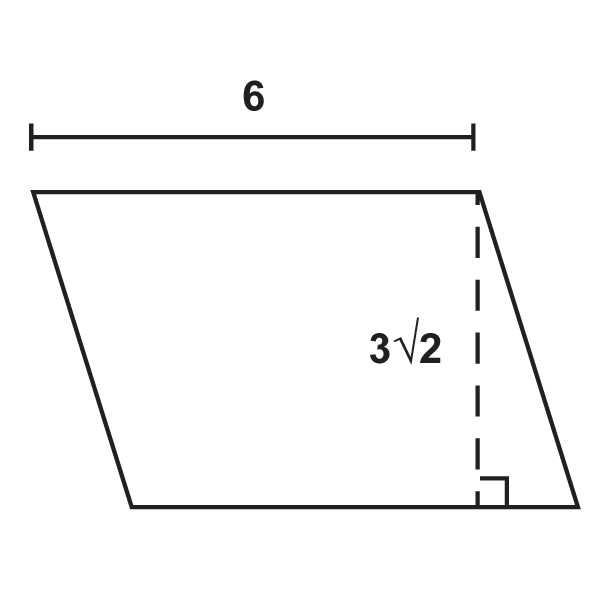
Figura\(\PageIndex{10}\) -
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) - Si el área de un paralelogramo es\(42\text{ units }^2\) y la base es\(6\text{ units }\), ¿cuál es la altura?
- Si el área de un paralelogramo es\(48\text{ units }^2\) y la altura es\(6\text{ units }\), ¿cuál es la base?
- Si la base de un paralelogramo es de 9 unidades y el área es\(108\text{ units }^2\), ¿cuál es la altura?
- Si la altura de un paralelogramo es de 11 unidades y el área es\(27.5\text{ units }^2\), ¿cuál es la base?
vocabulario
| Término | Definición |
|---|---|
| zona | La cantidad de espacio dentro de una figura. El área se mide en unidades cuadradas. |
| perímetro | La distancia alrededor de una forma. El perímetro de cualquier figura debe tener una unidad de medida adherida al mismo. Si no se dan unidades específicas (pies, pulgadas, centímetros, etc), escriba unidades. |
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Área de un paralelogramo | El área de un paralelogramo es igual a la base multiplicada por la altura:\(A = bh\). La altura de un paralelogramo siempre es perpendicular a la base (los lados no son la altura). |
Recursos adicionales
Elemento Interactivo
Video: Área de un Paralelogramo (Números Enteros)
Actividades: Área de un Paralelogramo Preguntas de Discusión
Ayudas de estudio: Guía de estudio de triángulos y cuadriláteros
Práctica: Área de un Paralelogramo
Mundo Real: Perímetro