Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

5.14: Área y Perímetro de Trapezoides

Última actualización

30 oct 2022
Guardar como PDF
- 5.13: Trapezoides
- 5.15: Área de Paralelogramos- Cuadrados, Rectángulos y Trapezoides

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

El área es la altura por el promedio de las bases; el perímetro es la suma de los lados.

Un trapecio es un cuadrilátero con un par de lados paralelos. Los lados paralelos se llaman las bases y nos referiremos a las longitudes de las bases como $b_1$ y $b_2$ . La distancia perpendicular entre los lados paralelos es la altura del trapecio. El área de un trapecio es $A=\dfrac{1}{2}h(b_1+b_2)$ donde siempre $h$ está perpendicular a las bases.

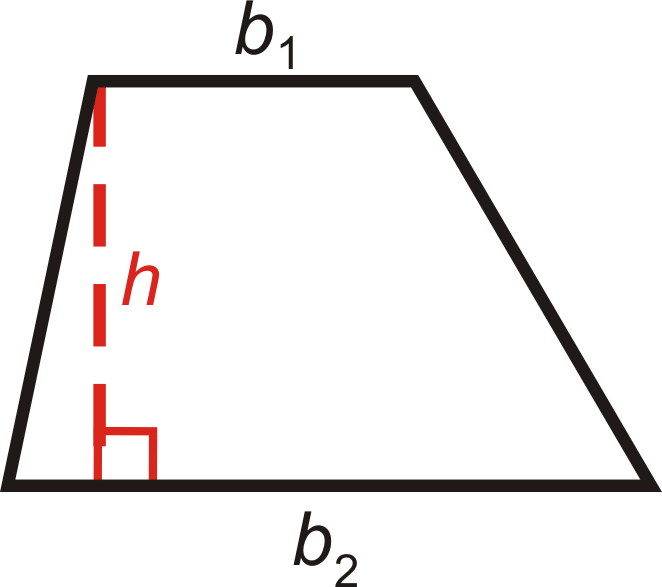
f-d_c1b06ab493bfb762ce7a00292eeb9fd1d51740ed61874be55029f0e3+image_tiny+image_tiny.png — Figura $\PageIndex{1}$

¿Y si te dieran un trapecio y el tamaño de sus dos bases así como su altura? ¿Cómo podrías encontrar la distancia total alrededor del trapecio y la cantidad de espacio que ocupa?

Ejemplo $\PageIndex{1}$

Encuentra el área del trapecio.

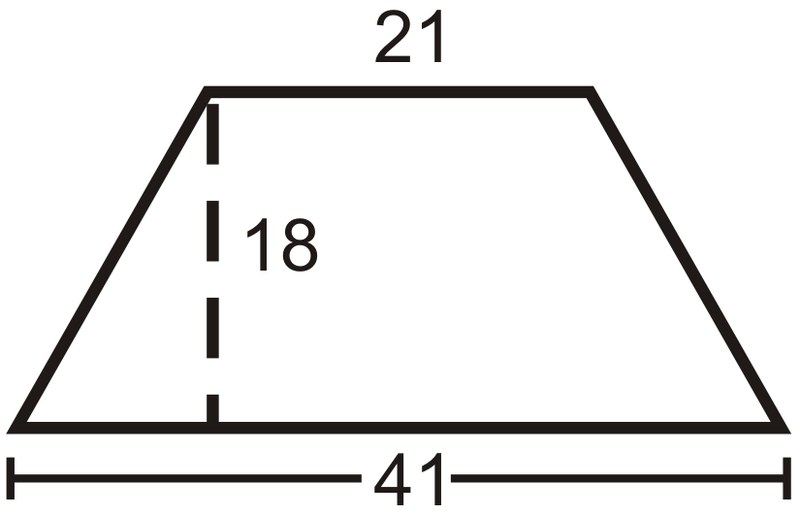
f-d_e764f1c3e83b3024cca4c061cbb134bbea2a05f4fd30ff0782ed47f8+image_tiny+image_tiny.png — Figura $\PageIndex{2}$

Solución

Usa la fórmula para el área de un trapecio.

$\dfrac{1}{2}(18)(41+21)=558\text{ units}^2$

Ejemplo $\PageIndex{2}$

Encuentra el área del trapecio. Redondea tus respuestas a la centésima más cercana.

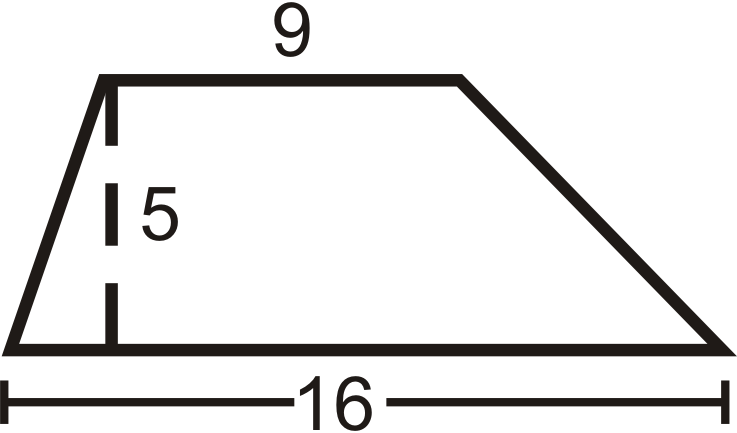
f-d_0dbc04261ca9bbb2ebf8c4cd0da2ed01cbc415d971c874bf94805f3e+image_tiny+image_tiny.png — Figura $\PageIndex{3}$

Solución

Usa la fórmula para el área de un trapecio.

$\dfrac{1}{2}(5)(16+9)=62.5\text{ units}^2$

Ejemplo $\PageIndex{3}$

Encuentra el área del trapecio.

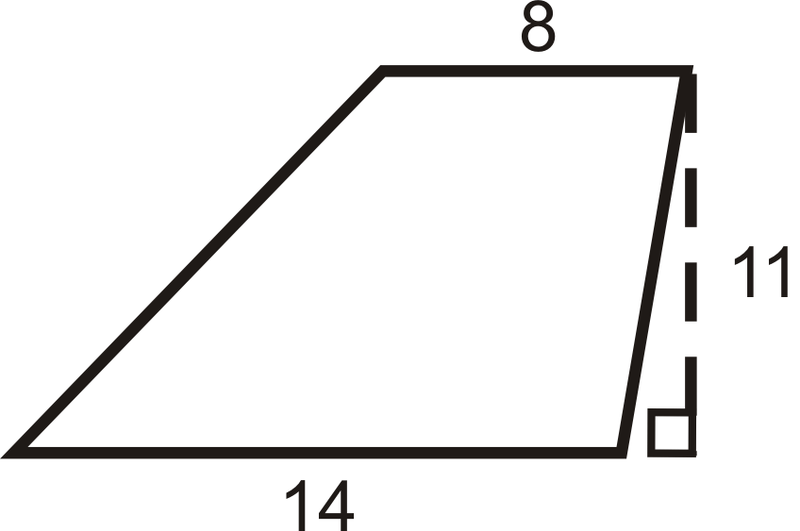
f-d_93929731e81fccbdeb0e48ec65c76cb9de3070945aa96ca9e6764cf7+image_tiny+image_tiny.png — Figura $\PageIndex{4}$

Solución

$\begin{aligned} A&=\dfrac{1}{2}(11)(14+8) \\ A&=\dfrac{1}{2}(11)(22) \\ A&=121\text{ units}^2\end{aligned}$

Ejemplo $\PageIndex{4}$

Encuentra el área del trapecio.

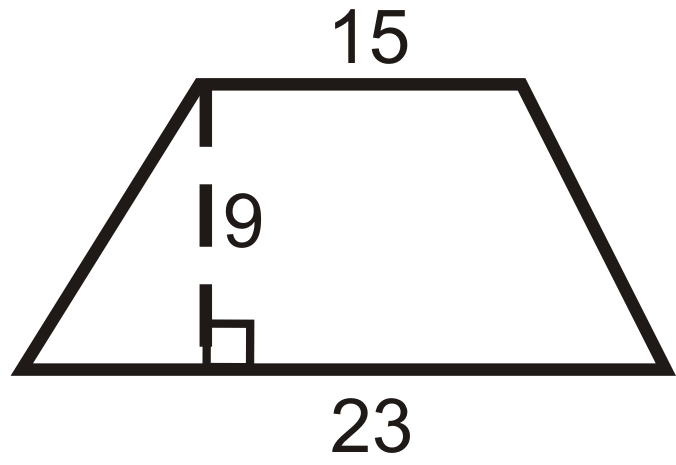
f-d_57e55cb65ba8a0c7f53e1a46f74ffe5f49301cdf6988bcbfd9a444a1+image_tiny+image_tiny.png — Figura $\PageIndex{5}$

Solución

$\begin{aligned} A&=\dfrac{1}{2}(9)(15+23) \\ A&=\dfrac{1}{2}(9)(38) \\ A&=171\text{ units}^2 \end{aligned}$

Ejemplo $\PageIndex{5}$

Encuentra el perímetro y el área del trapecio.

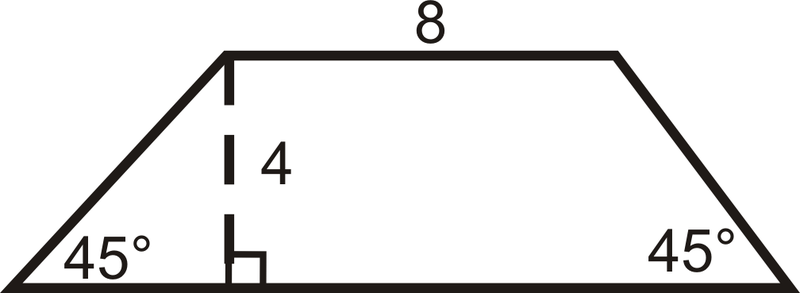
F-D_4a742e4f3d7ffe2227d6c71cd43ab769fdaddebfb899185eeb566908+image_tiny+image_tiny.png — Figura $\PageIndex{6}$

Solución

A pesar de que no se nos dice la longitud de la segunda base, podemos encontrarla usando triángulos rectos especiales. Ambos triángulos en los extremos de este trapecio son triángulos rectos isósceles, por lo que las hipotenusas son $4\sqrt{2}$ y las otras patas son de longitud 4.

$\begin{aligned} P&=8+4\sqrt{2}+16+4\sqrt{2} &\qquad A&=\dfrac{1}{2}(4)(8+16) \\ P&=24+8\sqrt{2}\approx 35.3\text{ units} & A&=48\text{ units}^2 \end{aligned}$

Revisar

Encuentra el área y perímetro de las siguientes formas. Redondea tus respuestas a la centésima más cercana.

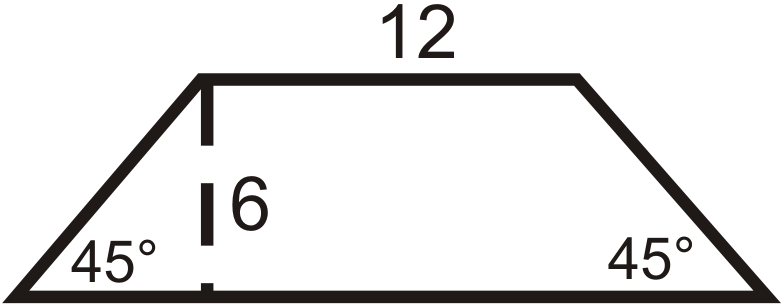
Figura $\PageIndex{7}$
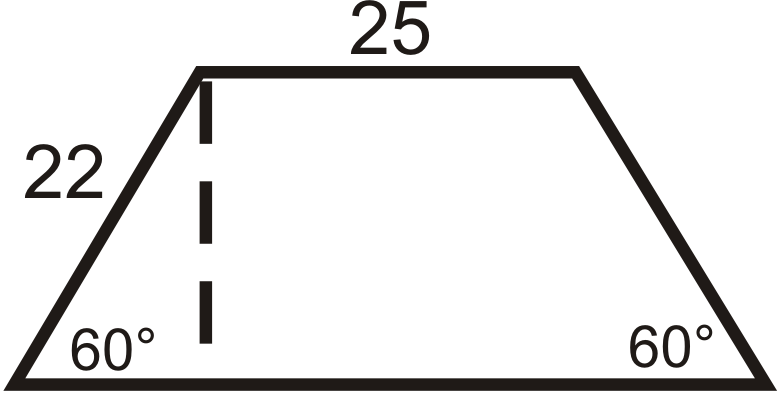
Figura $\PageIndex{8}$

Encuentra el área de los siguientes trapecios.

Trapezoide con bases de 3 y 7 pulgadas y altura de 3 pulgadas.
Trapezoide con bases de 6 y 8 pulgadas y altura de 5 pulgadas.
Trapezoide con bases de 10 y 26 pulgadas y altura de 2 pulgadas.
Trapezoide con bases de 15 y 12 pulgadas y altura de 10 pulgadas.
Trapezoide con bases de 4 y 23 pulgadas y altura de 21 pulgadas.
Trapezoide con bases de 9 y 4 pulgadas y altura de 1 pulg.
Trapezoide con bases de 12 y 8 pulgadas y altura de 16 pulgadas.
Trapezoide con bases de 26 y 14 pulgadas y altura de 19 pulgadas.

Utilice las cifras dadas para responder a las preguntas.

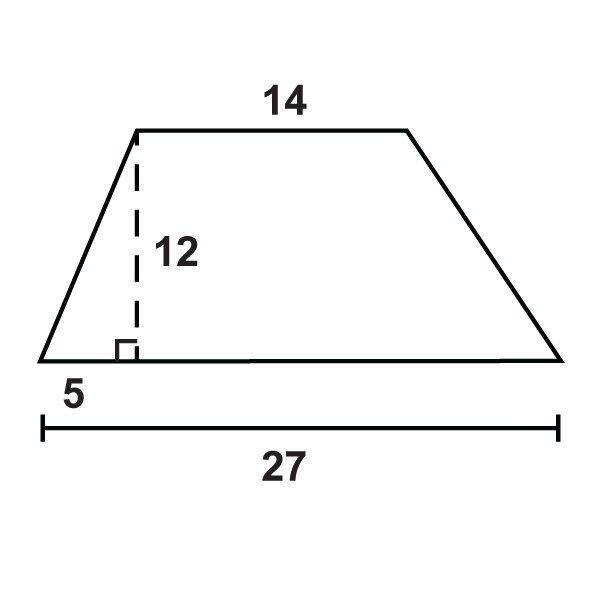
f-d_66f889271da061c075e7f3293ecdbd11de4f7ca927f17d80ac954b9f+image_tiny+image_tiny.png — Figura $\PageIndex{9}$

¿Cuál es el perímetro del trapecio?
¿Cuál es el área del trapecio?

f-d_3aca86122b2468a1535858022292851bd15bbc4b5833f747818a0f11+image_tiny+image_tiny+image_tiny.png — Figura $\PageIndex{10}$

¿Cuál es el perímetro del trapecio?
¿Cuál es el área del trapecio?

f-d_dd33de75c7638bc7e2e588ff9dedc1e5e5675a9f13703529771eae31+image_tiny+image_tiny.png — Figura $\PageIndex{11}$

¿Cuál es el perímetro del trapecio?
¿Cuál es el área del trapecio?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.5.

El vocabulario

Término	Definición
zona	La cantidad de espacio dentro de una figura. El área se mide en unidades cuadradas.
trapecio isósceles	Un *trapecio isósceles* es un trapecio donde los lados no paralelos son congruentes.
segmento medio (de un trapecio)	Un segmento de línea que conecta los puntos medios de los lados no paralelos.
perímetro	La distancia alrededor de una forma. El perímetro de cualquier figura debe tener una unidad de medida adherida al mismo. Si no se dan unidades específicas (pies, pulgadas, centímetros, etc), escriba *unidades.*
trapecio	Un cuadrilátero con exactamente un par de lados paralelos.

Recursos adicionales

Elemento interactivo

Video: Ejemplos de Área y Perímetro de Trapezoides - Básico

Actividades: Área y Perímetro de Trapezoides Preguntas de Discusión

Ayudas de estudio: Guía de estudio de triángulos y cuadriláteros

Práctica: Área y Perímetro de Trapezoides

Mundo Real: Perímetro

Revisar

Reseña (Respuestas)

El vocabulario

Recursos adicionales

Support Center

How can we help?